back propagation

In machine learning, backpropagation is a gradient computation method commonly used for training a neural network to compute its parameter updates.

It is an efficient application of the chain rule to neural networks. Backpropagation computes the gradient of a loss function with respect to the weights of the network for a single input–output example, and does so efficiently, computing the gradient one layer at a time, iterating backward from the last layer to avoid redundant calculations of intermediate terms in the chain rule; this can be derived through dynamic programming.

Strictly speaking, the term ''backpropagation'' refers only to an algorithm for efficiently computing the gradient, not how the gradient is used; but the term is often used loosely to refer to the entire learning algorithm – including how the gradient is used, such as by stochastic gradient descent, or as an intermediate step in a more complicated optimizer, such as Adaptive Moment Estimation. The local minimum convergence, exploding gradient, vanishing gradient, and weak control of learning rate are main disadvantages of these optimization algorithms. The Hessian and quasi-Hessian optimizers solve only local minimum convergence problem, and the backpropagation works longer. These problems caused researchers to develop hybrid and fractional optimization algorithms.

Backpropagation had multiple discoveries and partial discoveries, with a tangled history and terminology. See the history section for details. Some other names for the technique include "reverse mode of automatic differentiation" or " reverse accumulation"., "The back-propagation algorithm described here is only one approach to automatic differentiation. It is a special case of a broader class of techniques called ''reverse mode accumulation''."

Overview

Backpropagation computes the gradient in weight space of a feedforward neural network, with respect to a loss function. Denote:
* $x$: input (vector of features)
* $y$: target output
*:For classification, output will be a vector of class probabilities (e.g., $(0.1, 0.7, 0.2)$, and target output is a specific class, encoded by the one-hot/ dummy variable (e.g., $(0, 1, 0)$).
* $C$: loss function or "cost function"
*:For classification, this is usually cross-entropy (XC, log loss), while for regression it is usually squared error loss (SEL).
* $L$: the number of layers
* $W^l = (w^l_)$: the weights between layer $l - 1$ and $l$, where $w^l_$ is the weight between the $k$-th node in layer $l - 1$ and the $j$-th node in layer $l$
* $f^l$: activation functions at layer $l$
*:For classification the last layer is usually the logistic function for binary classification, and softmax (softargmax) for multi-class classification, while for the hidden layers this was traditionally a sigmoid function (logistic function or others) on each node (coordinate), but today is more varied, with rectifier ( ramp, ReLU) being common.
* $a^l_j$: activation of the $j$-th node in layer $l$.

In the derivation of backpropagation, other intermediate quantities are used by introducing them as needed below. Bias terms are not treated specially since they correspond to a weight with a fixed input of 1. For backpropagation the specific loss function and activation functions do not matter as long as they and their derivatives can be evaluated efficiently. Traditional activation functions include sigmoid, tanh, and ReLU. Swish, mish, and other activation functions have since been proposed as well.

The overall network is a combination of function composition and matrix multiplication:
:$g(x) := f^L(W^L f^(W^ \cdots f^1(W^1 x)\cdots))$

For a training set there will be a set of input–output pairs, $\left\$. For each input–output pair $(x_i, y_i)$ in the training set, the loss of the model on that pair is the cost of the difference between the predicted output $g(x_i)$ and the target output $y_i$:
:$C(y_i, g(x_i))$

Note the distinction: during model evaluation the weights are fixed while the inputs vary (and the target output may be unknown), and the network ends with the output layer (it does not include the loss function). During model training the input–output pair is fixed while the weights vary, and the network ends with the loss function.

Backpropagation computes the gradient for a ''fixed'' input–output pair $(x_i, y_i)$, where the weights $w^l_$ can vary. Each individual component of the gradient, $\partial C/\partial w^l_,$ can be computed by the chain rule; but doing this separately for each weight is inefficient. Backpropagation efficiently computes the gradient by avoiding duplicate calculations and not computing unnecessary intermediate values, by computing the gradient of each layer – specifically the gradient of the weighted ''input'' of each layer, denoted by $\delta^l$ – from back to front.

Informally, the key point is that since the only way a weight in $W^l$ affects the loss is through its effect on the ''next'' layer, and it does so ''linearly'', $\delta^l$ are the only data you need to compute the gradients of the weights at layer $l$, and then the gradients of weights of previous layer can be computed by $\delta^$ and repeated recursively. This avoids inefficiency in two ways. First, it avoids duplication because when computing the gradient at layer $l$, it is unnecessary to recompute all derivatives on later layers $l+1, l+2, \ldots$ each time. Second, it avoids unnecessary intermediate calculations, because at each stage it directly computes the gradient of the weights with respect to the ultimate output (the loss), rather than unnecessarily computing the derivatives of the values of hidden layers with respect to changes in weights $\partial a^_/\partial w^l_$.

Backpropagation can be expressed for simple feedforward networks in terms of matrix multiplication, or more generally in terms of the adjoint graph.

Matrix multiplication

For the basic case of a feedforward network, where nodes in each layer are connected only to nodes in the immediate next layer (without skipping any layers), and there is a loss function that computes a scalar loss for the final output, backpropagation can be understood simply by matrix multiplication. Essentially, backpropagation evaluates the expression for the derivative of the cost function as a product of derivatives between each layer ''from right to left'' – "backwards" – with the gradient of the weights between each layer being a simple modification of the partial products (the "backwards propagated error").

Given an input–output pair $(x, y)$, the loss is:

:$C(y, f^L(W^L f^(W^ \cdots f^2(W^2 f^1(W^1 x))\cdots)))$

To compute this, one starts with the input $x$ and works forward; denote the weighted input of each hidden layer as $z^l$ and the output of hidden layer $l$ as the activation $a^l$. For backpropagation, the activation $a^l$ as well as the derivatives $(f^l)'$ (evaluated at $z^l$) must be cached for use during the backwards pass.

The derivative of the loss in terms of the inputs is given by the chain rule; note that each term is a total derivative, evaluated at the value of the network (at each node) on the input $x$:

:$\frac\cdot \frac \cdot \frac \cdot \frac\cdot \frac \cdot \ldots \cdot \frac \cdot \frac,$
where $\frac$ is a diagonal matrix.

These terms are: the derivative of the loss function; the derivatives of the activation functions; and the matrices of weights:
:$\frac\circ (f^L)' \cdot W^L \circ (f^)' \cdot W^ \circ \cdots \circ (f^1)' \cdot W^1.$

The gradient $\nabla$ is the transpose of the derivative of the output in terms of the input, so the matrices are transposed and the order of multiplication is reversed, but the entries are the same:
:$\nabla_x C = (W^1)^T \cdot (f^1)' \circ \ldots \circ (W^)^T \cdot (f^)' \circ (W^L)^T \cdot (f^L)' \circ \nabla_ C.$

Backpropagation then consists essentially of evaluating this expression from right to left (equivalently, multiplying the previous expression for the derivative from left to right), computing the gradient at each layer on the way; there is an added step, because the gradient of the weights is not just a subexpression: there's an extra multiplication.

Introducing the auxiliary quantity $\delta^l$ for the partial products (multiplying from right to left), interpreted as the "error at level $l$" and defined as the gradient of the input values at level $l$:
:$\delta^l := (f^l)' \circ (W^)^T\cdot(f^)' \circ \cdots \circ (W^)^T \cdot (f^)' \circ (W^L)^T \cdot (f^L)' \circ \nabla_ C.$
Note that $\delta^l$ is a vector, of length equal to the number of nodes in level $l$; each component is interpreted as the "cost attributable to (the value of) that node".

The gradient of the weights in layer $l$ is then:
:$\nabla_ C = \delta^l(a^)^T.$
The factor of $a^$ is because the weights $W^l$ between level $l - 1$ and $l$ affect level $l$ proportionally to the inputs (activations): the inputs are fixed, the weights vary.

The $\delta^l$ can easily be computed recursively, going from right to left, as:
:$\delta^ := (f^)' \circ (W^l)^T \cdot \delta^l.$

The gradients of the weights can thus be computed using a few matrix multiplications for each level; this is backpropagation.

Compared with naively computing forwards (using the $\delta^l$ for illustration):

:$\begin \delta^1 &= (f^1)' \circ (W^2)^T \cdot (f^2)' \circ \cdots \circ (W^)^T \cdot (f^)' \circ (W^L)^T \cdot (f^L)' \circ \nabla_ C\\ \delta^2 &= (f^2)' \circ \cdots \circ (W^)^T \cdot (f^)' \circ (W^L)^T \cdot (f^L)' \circ \nabla_ C\\ &\vdots\\ \delta^ &= (f^)' \circ (W^L)^T \cdot (f^L)' \circ \nabla_ C\\ \delta^L &= (f^L)' \circ \nabla_ C, \end$

There are two key differences with backpropagation:

# Computing $\delta^$ in terms of $\delta^l$ avoids the obvious duplicate multiplication of layers $l$ and beyond.
# Multiplying starting from $\nabla_ C$ – propagating the error ''backwards'' – means that each step simply multiplies a vector ($\delta^l$) by the matrices of weights $(W^l)^T$ and derivatives of activations $(f^)'$. By contrast, multiplying forwards, starting from the changes at an earlier layer, means that each multiplication multiplies a ''matrix'' by a ''matrix''. This is much more expensive, and corresponds to tracking every possible path of a change in one layer $l$ forward to changes in the layer $l+2$ (for multiplying $W^$ by $W^$, with additional multiplications for the derivatives of the activations), which unnecessarily computes the intermediate quantities of how weight changes affect the values of hidden nodes.

Adjoint graph

For more general graphs, and other advanced variations, backpropagation can be understood in terms of automatic differentiation, where backpropagation is a special case of reverse accumulation (or "reverse mode").

Intuition

Motivation

The goal of any supervised learning algorithm is to find a function that best maps a set of inputs to their correct output. The motivation for backpropagation is to train a multi-layered neural network such that it can learn the appropriate internal representations to allow it to learn any arbitrary mapping of input to output.

Learning as an optimization problem

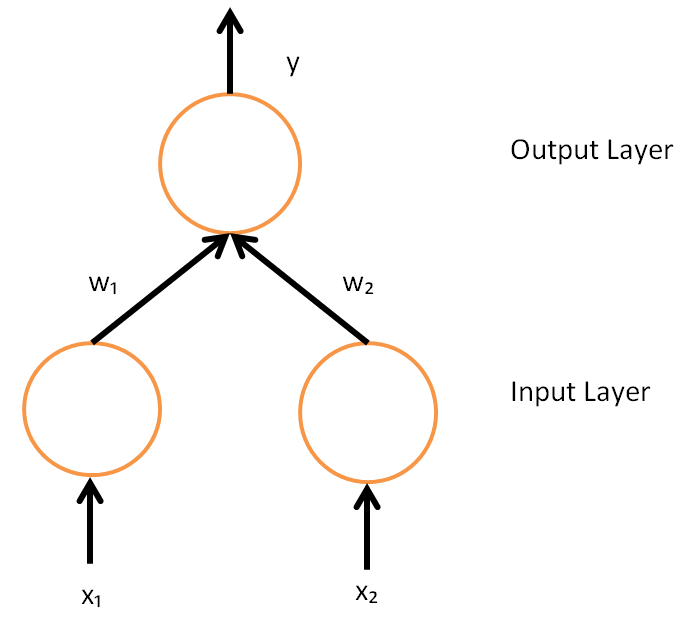
To understand the mathematical derivation of the backpropagation algorithm, it helps to first develop some intuition about the relationship between the actual output of a neuron and the correct output for a particular training example. Consider a simple neural network with two input units, one output unit and no hidden units, and in which each neuron uses a linear output (unlike most work on neural networks, in which mapping from inputs to outputs is non-linear) that is the weighted sum of its input.

Initially, before training, the weights will be set randomly. Then the neuron learns from training examples, which in this case consist of a set of tuples $(x_1, x_2, t)$ where $x_1$ and $x_2$ are the inputs to the network and is the correct output (the output the network should produce given those inputs, when it has been trained). The initial network, given $x_1$ and $x_2$, will compute an output that likely differs from (given random weights). A loss function $L(t, y)$ is used for measuring the discrepancy between the target output and the computed output . For regression analysis problems the squared error can be used as a loss function, for classification the categorical cross-entropy can be used.

As an example consider a regression problem using the square error as a loss:
:$L(t, y)= (t-y)^2 = E,$

where is the discrepancy or error.
Consider the network on a single training case: $(1, 1, 0)$. Thus, the input $x_1$ and $x_2$ are 1 and 1 respectively and the correct output, is 0. Now if the relation is plotted between the network's output on the horizontal axis and the error on the vertical axis, the result is a parabola. The minimum of the parabola corresponds to the output which minimizes the error . For a single training case, the minimum also touches the horizontal axis, which means the error will be zero and the network can produce an output that exactly matches the target output . Therefore, the problem of mapping inputs to outputs can be reduced to an optimization problem of finding a function that will produce the minimal error.

However, the output of a neuron depends on the weighted sum of all its inputs:

:$y=x_1w_1 + x_2w_2,$

where $w_1$ and $w_2$ are the weights on the connection from the input units to the output unit. Therefore, the error also depends on the incoming weights to the neuron, which is ultimately what needs to be changed in the network to enable learning.

In this example, upon injecting the training data $(1, 1, 0)$, the loss function becomes

$E = (t-y)^2 = y^2 = (x_1w_1 + x_2w_2)^2 = (w_1 + w_2)^2.$

Then, the loss function $E$ takes the form of a parabolic cylinder with its base directed along $w_1 = -w_2$. Since all sets of weights that satisfy $w_1 = -w_2$ minimize the loss function, in this case additional constraints are required to converge to a unique solution. Additional constraints could either be generated by setting specific conditions to the weights, or by injecting additional training data.

One commonly used algorithm to find the set of weights that minimizes the error is gradient descent. By backpropagation, the steepest descent direction is calculated of the loss function versus the present synaptic weights. Then, the weights can be modified along the steepest descent direction, and the error is minimized in an efficient way.

Derivation

The gradient descent method involves calculating the derivative of the loss function with respect to the weights of the network. This is normally done using backpropagation. Assuming one output neuron, the squared error function is

:$E = L(t, y)$

where
:$L$ is the loss for the output $y$ and target value $t$,
:$t$ is the target output for a training sample, and
:$y$ is the actual output of the output neuron.

For each neuron $j$, its output $o_j$ is defined as

:$o_j = \varphi(\text_j) = \varphi\left(\sum_^n w_x_k\right),$

where the activation function $\varphi$ is non-linear and differentiable over the activation region (the ReLU is not differentiable at one point). A historically used activation function is the logistic function:

:$\varphi(z) = \frac 1$

which has a convenient derivative of:

:$\frac = \varphi(z)(1-\varphi(z))$

The input $\text_j$ to a neuron is the weighted sum of outputs $o_k$ of previous neurons. If the neuron is in the first layer after the input layer, the $o_k$ of the input layer are simply the inputs $x_k$ to the network. The number of input units to the neuron is $n$. The variable $w_$ denotes the weight between neuron $k$ of the previous layer and neuron $j$ of the current layer.

Finding the derivative of the error

Calculating the partial derivative of the error with respect to a weight $w_$ is done using the chain rule twice:

In the last factor of the right-hand side of the above, only one term in the sum $\text_j$ depends on $w_$, so that

If the neuron is in the first layer after the input layer, $o_i$ is just $x_i$.

The derivative of the output of neuron $j$ with respect to its input is simply the partial derivative of the activation function:

which for the logistic activation function
:$\frac = \frac \varphi(\text_j) = \varphi(\text_j)(1-\varphi(\text_j)) = o_j(1-o_j)$

This is the reason why backpropagation requires that the activation function be differentiable. (Nevertheless, the ReLU activation function, which is non-differentiable at 0, has become quite popular, e.g. in AlexNet)

The first factor is straightforward to evaluate if the neuron is in the output layer, because then $o_j = y$ and

If half of the square error is used as loss function we can rewrite it as

: $\frac = \frac = \frac \frac(t - y)^2 = y - t$

However, if $j$ is in an arbitrary inner layer of the network, finding the derivative $E$ with respect to $o_j$ is less obvious.

Considering $E$ as a function with the inputs being all neurons $L = \$ receiving input from neuron $j$,

: $\frac = \frac$

and taking the total derivative with respect to $o_j$, a recursive expression for the derivative is obtained:

Therefore, the derivative with respect to $o_j$ can be calculated if all the derivatives with respect to the outputs $o_\ell$ of the next layer – the ones closer to the output neuron – are known. [Note, if any of the neurons in set $L$ were not connected to neuron $j$, they would be independent of $w_$ and the corresponding partial derivative under the summation would vanish to 0.]

Substituting , and in we obtain:

: $\frac = \frac \frac \frac = \frac \frac o_i$
: $\frac = o_i \delta_j$

with

:$\delta_j = \frac \frac = \begin \frac \frac & \text j \text\\ (\sum_ w_ \delta_\ell)\frac & \text j \text \end$

if $\varphi$ is the logistic function, and the error is the square error:

: $\delta_j = \frac \frac = \begin (o_j-t_j)o_j(1-o_) & \text j \text\\ (\sum_ w_ \delta_\ell)o_j(1-o_j) & \text j \text \end$

To update the weight $w_$ using gradient descent, one must choose a learning rate, $\eta >0$. The change in weight needs to reflect the impact on $E$ of an increase or decrease in $w_$. If $\frac > 0$, an increase in $w_$ increases $E$; conversely, if $\frac < 0$, an increase in $w_$ decreases $E$. The new $\Delta w_$ is added to the old weight, and the product of the learning rate and the gradient, multiplied by $-1$ guarantees that $w_$ changes in a way that always decreases $E$. In other words, in the equation immediately below, $- \eta \frac$ always changes $w_$ in such a way that $E$ is decreased:

: $\Delta w_ = - \eta \frac = - \eta o_i \delta_j$

Second-order gradient descent

Using a Hessian matrix of second-order derivatives of the error function, the Levenberg–Marquardt algorithm often converges faster than first-order gradient descent, especially when the topology of the error function is complicated. It may also find solutions in smaller node counts for which other methods might not converge. The Hessian can be approximated by the Fisher information matrix.

As an example, consider a simple feedforward network. At the $l$-th layer, we have$x^_i, \quad a^_i = f(x^_i), \quad x^_i = \sum_j W_ a^_j$where $x$ are the pre-activations, $a$ are the activations, and $W$ is the weight matrix. Given a loss function $L$, the first-order backpropagation states that$\frac = \sum_j W_\frac, \quad \frac = f'(x_j^)\frac$and the second-order backpropagation states that$\frac = \sum_ W_W_\frac, \quad \frac = f'(x_^) f'(x_^) \frac + \delta_ f''(x^_ ) \frac$where $\delta$ is the Dirac delta symbol.

Arbitrary-order derivatives in arbitrary computational graphs can be computed with backpropagation, but with more complex expressions for higher orders.

Loss function

The loss function is a function that maps values of one or more variables onto a real number intuitively representing some "cost" associated with those values. For backpropagation, the loss function calculates the difference between the network output and its expected output, after a training example has propagated through the network.

Assumptions

The mathematical expression of the loss function must fulfill two conditions in order for it to be possibly used in backpropagation. The first is that it can be written as an average $E=\frac\sum_xE_x$ over error functions $E_x$, for $n$ individual training examples, $x$. The reason for this assumption is that the backpropagation algorithm calculates the gradient of the error function for a single training example, which needs to be generalized to the overall error function. The second assumption is that it can be written as a function of the outputs from the neural network.

Example loss function

Let $y,y'$ be vectors in $\mathbb^n$.

Select an error function $E(y,y')$ measuring the difference between two outputs. The standard choice is the square of the Euclidean distance between the vectors $y$ and $y'$:$E(y,y') = \tfrac \lVert y-y'\rVert^2$The error function over $n$ training examples can then be written as an average of losses over individual examples:$E=\frac\sum_x\lVert (y(x)-y'(x)) \rVert^2$

Limitations

* Gradient descent with backpropagation is not guaranteed to find the global minimum of the error function, but only a local minimum; also, it has trouble crossing plateaus in the error function landscape. This issue, caused by the non-convexity of error functions in neural networks, was long thought to be a major drawback, but Yann LeCun ''et al.'' argue that in many practical problems, it is not.
* Backpropagation learning does not require normalization of input vectors; however, normalization could improve performance.
* Backpropagation requires the derivatives of activation functions to be known at network design time.

History

Precursors

Backpropagation had been derived repeatedly, as it is essentially an efficient application of the chain rule (first written down by Gottfried Wilhelm Leibniz in 1676) to neural networks.

The terminology "back-propagating error correction" was introduced in 1962 by Frank Rosenblatt, but he did not know how to implement this. In any case, he only studied neurons whose outputs were discrete levels, which only had zero derivatives, making backpropagation impossible.

Precursors to backpropagation appeared in optimal control theory since 1950s. Yann LeCun et al credits 1950s work by Pontryagin and others in optimal control theory, especially the adjoint state method, for being a continuous-time version of backpropagation. Hecht-Nielsen credits the Robbins–Monro algorithm (1951) and Arthur Bryson and Yu-Chi Ho's ''Applied Optimal Control'' (1969) as presages of backpropagation. Other precursors were Henry J. Kelley 1960, and Arthur E. Bryson (1961). In 1962, Stuart Dreyfus published a simpler derivation based only on the chain rule. In 1973, he adapted parameters of controllers in proportion to error gradients. Unlike modern backpropagation, these precursors used standard Jacobian matrix calculations from one stage to the previous one, neither addressing direct links across several stages nor potential additional efficiency gains due to network sparsity.

The ADALINE (1960) learning algorithm was gradient descent with a squared error loss for a single layer. The first multilayer perceptron (MLP) with more than one layer trained by stochastic gradient descent was published in 1967 by Shun'ichi Amari. The MLP had 5 layers, with 2 learnable layers, and it learned to classify patterns not linearly separable.

Modern backpropagation

Modern backpropagation was first published by Seppo Linnainmaa as "reverse mode of automatic differentiation" (1970) for discrete connected networks of nested differentiable functions.

In 1982, Paul Werbos applied backpropagation to MLPs in the way that has become standard. Werbos described how he developed backpropagation in an interview. In 1971, during his PhD work, he developed backpropagation to mathematicize Freud's "flow of psychic energy". He faced repeated difficulty in publishing the work, only managing in 1981. He also claimed that "the first practical application of back-propagation was for estimating a dynamic model to predict nationalism and social communications in 1974" by him.

Around 1982, David E. Rumelhart independently developed backpropagation and taught the algorithm to others in his research circle. He did not cite previous work as he was unaware of them. He published the algorithm first in a 1985 paper, then in a 1986 ''Nature'' paper an experimental analysis of the technique. These papers became highly cited, contributed to the popularization of backpropagation, and coincided with the resurging research interest in neural networks during the 1980s.

In 1985, the method was also described by David Parker. Yann LeCun proposed an alternative form of backpropagation for neural networks in his PhD thesis in 1987.

Gradient descent took a considerable amount of time to reach acceptance. Some early objections were: there were no guarantees that gradient descent could reach a global minimum, only local minimum; neurons were "known" by physiologists as making discrete signals (0/1), not continuous ones, and with discrete signals, there is no gradient to take. See the interview with Geoffrey Hinton, who was awarded the 2024 Nobel Prize in Physics for his contributions to the field.

Early successes

Contributing to the acceptance were several applications in training neural networks via backpropagation, sometimes achieving popularity outside the research circles.

In 1987, NETtalk learned to convert English text into pronunciation. Sejnowski tried training it with both backpropagation and Boltzmann machine, but found the backpropagation significantly faster, so he used it for the final NETtalk. The NETtalk program became a popular success, appearing on the ''Today'' show.

In 1989, Dean A. Pomerleau published ALVINN, a neural network trained to drive autonomously using backpropagation.

The LeNet was published in 1989 to recognize handwritten zip codes.

In 1992, TD-Gammon achieved top human level play in backgammon. It was a reinforcement learning agent with a neural network with two layers, trained by backpropagation.

In 1993, Eric Wan won an international pattern recognition contest through backpropagation.

After backpropagation

During the 2000s it fell out of favour, but returned in the 2010s, benefiting from cheap, powerful GPU-based computing systems. This has been especially so in speech recognition, machine vision, natural language processing, and language structure learning research (in which it has been used to explain a variety of phenomena related to first and second language learning.)

Error backpropagation has been suggested to explain human brain event-related potential (ERP) components like the N400 and P600.

In 2023, a backpropagation algorithm was implemented on a photonic processor by a team at Stanford University.

See also

* Artificial neural network
* Neural circuit
* Catastrophic interference
* Ensemble learning
* AdaBoost
* Overfitting
* Neural backpropagation
* Backpropagation through time
* Backpropagation through structure
* Three-factor learning

Notes

References

Further reading

*
*
*
*

External links

* Backpropagation neural network tutorial at the Wikiversity
*
*
*
*

{{Authority control

Machine learning algorithms
Artificial neural networks