|
Tanh
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions are used to express the angle of parallelism in hyperbolic geometry. They are used to express Lorentz boosts as hyperbolic rotations in special relativity. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, and fluid dynamics. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictionary'', p. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Inverse Hyperbolic Functions
In mathematics, the inverse hyperbolic functions are inverses of the hyperbolic functions, analogous to the inverse circular functions. There are six in common use: inverse hyperbolic sine, inverse hyperbolic cosine, inverse hyperbolic tangent, inverse hyperbolic cosecant, inverse hyperbolic secant, and inverse hyperbolic cotangent. They are commonly denoted by the symbols for the hyperbolic functions, prefixed with ''arc-'' or ''ar-'' or with a superscript (for example , , or \sinh^). For a given value of a hyperbolic function, the inverse hyperbolic function provides the corresponding hyperbolic angle measure, for example \operatorname(\sinh a) = a and \sinh(\operatorname x) = x. Hyperbolic angle measure is the length of an arc of a unit hyperbola x^2 - y^2 = 1 as measured in the Lorentzian plane (''not'' the length of a hyperbolic arc in the Euclidean plane), and twice the area of the corresponding hyperbolic sector. This is analogous to the way circular angle measure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sinh Cosh Tanh
Sinh may refer to: * Hyperbolic sine, abbreviated as ''sinh'', a mathematical function * Sinh (clothing), a traditional women's garment from Southeast Asia * Singh, an Indian title and personal name * Sinhala script (ISO 15924 abbreviation: Sinh) See also * * SIMH, an emulator software * Sinha {{Disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, and applied mathematics, as well as in physics, including the branches of hydrodynamics, thermodynamics, quantum mechanics, and twistor theory. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to the sum function given by its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable, that is, '' holomorphic functions''. The concept can be extended to functions of several complex variables. Complex analysis is contrasted with real analysis, which dea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperbolic Sector
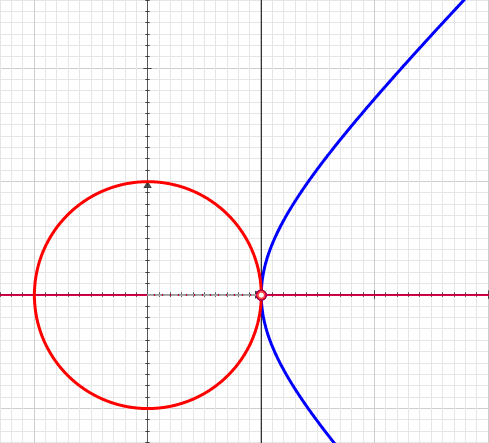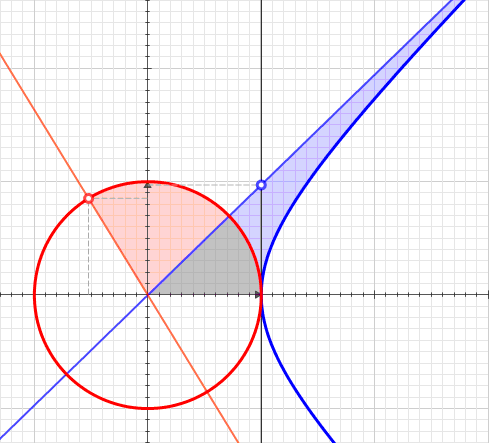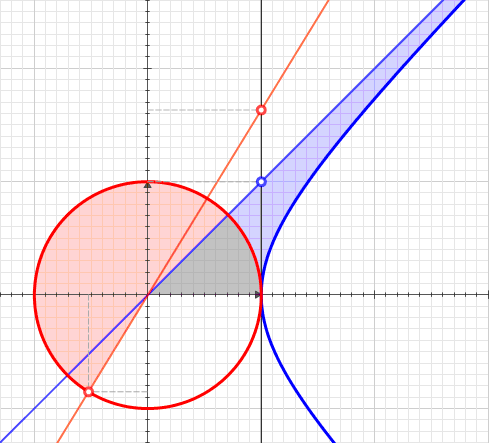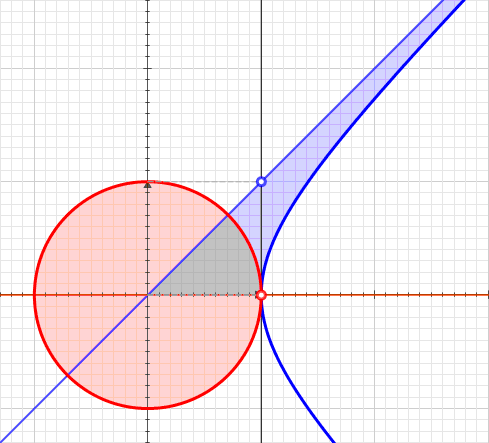
A hyperbolic sector is a region (mathematics), region of the Cartesian plane bounded by a hyperbola and two ray (geometry), rays from the origin to it. For example, the two points and on the Hyperbola#Rectangular hyperbola, rectangular hyperbola , or the corresponding region when this hyperbola is re-scaled and its orientation (geometry), orientation is altered by a Rotation (geometry), rotation leaving the center at the origin, as with the Unit hyperbola#Parametrization, unit hyperbola. A hyperbolic sector in standard position has and . The argument of hyperbolic functions is the hyperbolic angle, which is defined as the area of a hyperbolic sector of the standard hyperbola ''xy'' = 1. This area is evaluated using natural logarithm. Hyperbolic triangle When in standard position, a hyperbolic sector determines a hyperbolic triangle, the right triangle with one vertex (geometry), vertex at the origin, base on the diagonal ray ''y'' = ''x'', and third vertex on the h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). Two different regions may have the same area (as in squaring the circle); by synecdoche, "area" sometimes is used to refer to the region, as in a " polygonal area". The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperbolic Angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrizes the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation. The hyperbola ''xy'' = 1 is rectangular with semi-major axis \sqrt 2, analogous to the circular angle equaling the area of a circular sector in a circle with radius \sqrt 2. Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular (trigonometric) functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables. Definition Consider the rectangular hyperbola \textstyle\, and (by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Argument Of A Function
In mathematics, an argument of a function is a value provided to obtain the function's result. It is also called an independent variable. For example, the binary function f(x,y) = x^2 + y^2 has two arguments, x and y, in an ordered pair (x, y). The hypergeometric function is an example of a four-argument function. The number of arguments that a function takes is called the ''arity'' of the function. A function that takes a single argument as input, such as f(x) = x^2, is called a unary function. A function of two or more variables is considered to have a domain consisting of ordered pairs or tuples of argument values. The argument of a circular function is an angle In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R .... The argument of a hyperbolic function is a hyperbolic ang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperbolic Functions-2
{{disambiguation ...
Hyperbolic may refer to: * of or pertaining to a hyperbola, a type of smooth curve lying in a plane in mathematics ** Hyperbolic geometry, a non-Euclidean geometry ** Hyperbolic functions, analogues of ordinary trigonometric functions, defined using the hyperbola * of or pertaining to hyperbole, the use of exaggeration as a rhetorical device or figure of speech * ''Hyperbolic'' (album), by Pnau, 2024 See also * Exaggeration * Hyperboloid In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Google Books
Google Books (previously known as Google Book Search, Google Print, and by its code-name Project Ocean) is a service from Google that searches the full text of books and magazines that Google has scanned, converted to text using optical character recognition (OCR), and stored in its digital database.The basic Google book link is found at: https://books.google.com/ . The "advanced" interface allowing more specific searches is found at: https://books.google.com/advanced_book_search Books are provided either by publishers and authors through the Google Books Partner Program, or by Google's library partners through the Library Project. Additionally, Google has partnered with a number of magazine publishers to digitize their archives. The Publisher Program was first known as Google Print when it was introduced at the Frankfurt Book Fair in October 2004. The Google Books Library Project, which scans works in the collections of library partners and adds them to the digital inventory, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dover Publications
Dover Publications, also known as Dover Books, is an American book publisher founded in 1941 by Hayward and Blanche Cirker. It primarily reissues books that are out of print from their original publishers. These are often, but not always, books in the public domain. The original published editions may be scarce or historically significant. Dover republishes these books, making them available at a significantly reduced cost. Classic reprints Dover reprints classic works of literature, classical sheet music, and public-domain images from the 18th and 19th centuries. Dover also publishes an extensive collection of mathematical, scientific, and engineering texts. It often targets its reprints at a niche market, such as woodworking. Starting in 2015, the company branched out into graphic novel reprints, overseen by Dover acquisitions editor and former comics writer and editor Drew Ford. Most Dover reprints are photo facsimiles of the originals, retaining the original pagination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |