|
Stochastic Approximation
Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations. In a nutshell, stochastic approximation algorithms deal with a function of the form f(\theta) = \operatorname E_ (\theta,\xi) which is the expected value of a function depending on a random variable \xi . The goal is to recover properties of such a function f without evaluating it directly. Instead, stochastic approximation algorithms use random samples of F(\theta,\xi) to efficiently approximate properties of f such as zeros or extrema. Recently, stochastic approximations have found extensive applications in the fields of statistics and machine lea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Jack Kiefer (statistician)
Jack Carl Kiefer (January 25, 1924 – August 10, 1981) was an American mathematical statistician at Cornell University (1952 to 1979) and the University of California, Berkeley (1979 to 1981). His research interests included the optimal design of experiments, which was his major research area, as well as a wide variety of topics in mathematical statistics. Biography Jack Kiefer was born in Cincinnati, Ohio, to Carl Jack Kiefer and Marguerite K. Rosenau. He began his undergraduate studies at the Massachusetts Institute of Technology in 1942, but left after one year, taking up a position as first lieutenant in the United States Army Air Forces during World War II, during which he taught about radar systems. In 1946, he returned to MIT, graduating with bachelor's and master's degrees in economics and engineering in 1948 under the supervision of Harold Freeman. He then began graduate studies at Columbia University, under the supervision of Abraham Wald and Jacob Wolfowitz, receiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Iterative Methods
In computational mathematics, an iterative method is a Algorithm, mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the ''i''-th approximation (called an "iterate") is derived from the previous ones. A specific implementation with Algorithm#Termination, termination criteria for a given iterative method like gradient descent, hill climbing, Newton's method, or Quasi-Newton method, quasi-Newton methods like Broyden–Fletcher–Goldfarb–Shanno algorithm, BFGS, is an algorithm of an iterative method or a method of successive approximation. An iterative method is called ''Convergent series, convergent'' if the corresponding sequence converges for given initial approximations. A mathematically rigorous convergence analysis of an iterative method is usually performed; however, heuristic-based iterative methods are also common. In contrast, direct methods attempt to solve the problem by a finit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
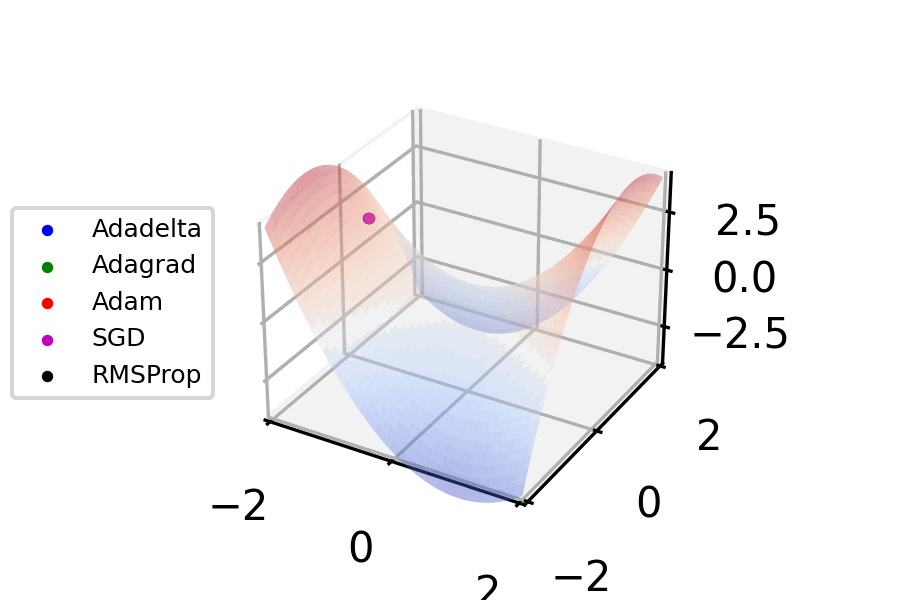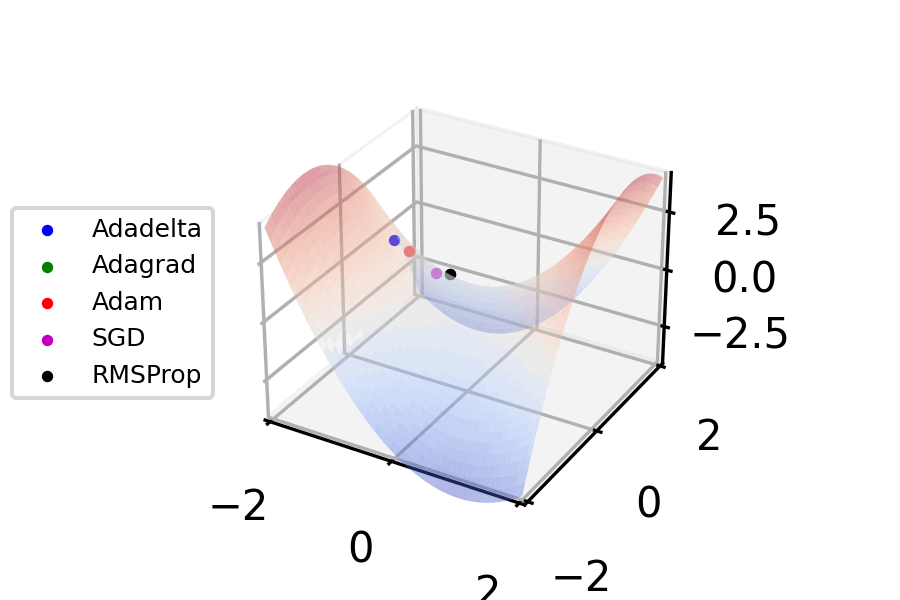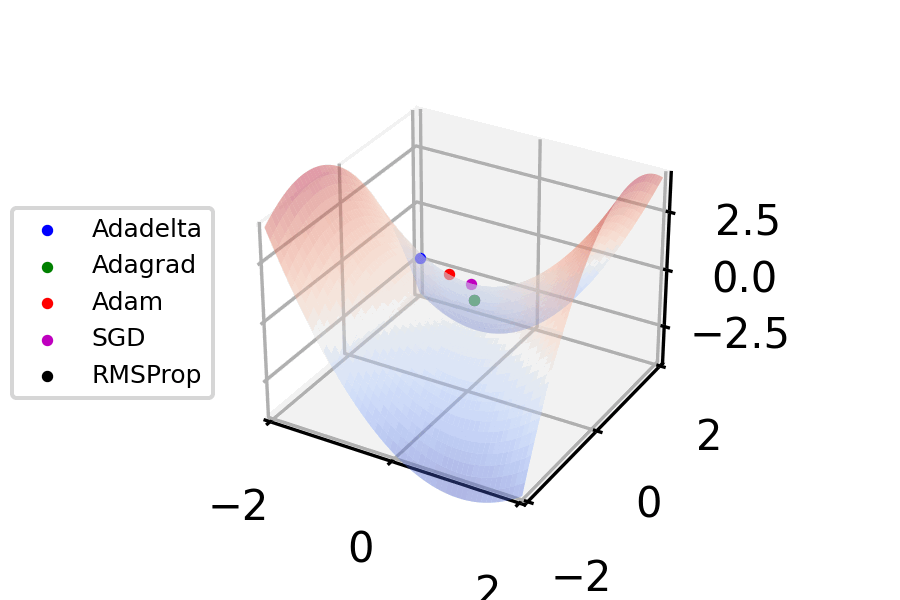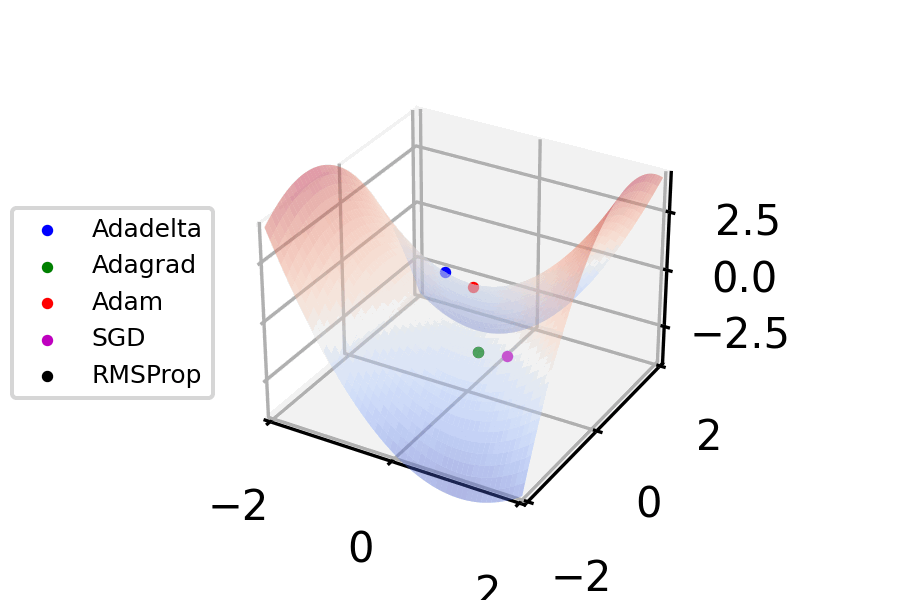
Stochastic Gradient Descent
Stochastic gradient descent (often abbreviated SGD) is an Iterative method, iterative method for optimizing an objective function with suitable smoothness properties (e.g. Differentiable function, differentiable or Subderivative, subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high Computational complexity, computational burden, achieving faster iterations in exchange for a lower Rate of convergence, convergence rate. The basic idea behind stochastic approximation can be traced back to the Robbins–Monro algorithm of the 1950s. Today, stochastic gradient descent has become an important optimization method in machine learning. Background Both statistics, statistical M-estimation, estimation and ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stochastic Variance Reduction
(Stochastic) variance reduction is an algorithmic approach to minimizing functions that can be decomposed into finite sums. By exploiting the finite sum structure, variance reduction techniques are able to achieve convergence rates that are impossible to achieve with methods that treat the objective as an infinite sum, as in the classical Stochastic approximation setting. Variance reduction approaches are widely used for training machine learning models such as logistic regression and support vector machines as these problems have finite-sum structure and uniform conditioning that make them ideal candidates for variance reduction. Finite sum objectives A function f is considered to have finite sum structure if it can be decomposed into a summation or average: :f(x) = \frac\sum_^n f_i(x), where the function value and derivative of each f_i can be queried independently. Although variance reduction methods can be applied for any positive n and any f_i structure, their favorable theor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stochastic Gradient Descent
Stochastic gradient descent (often abbreviated SGD) is an Iterative method, iterative method for optimizing an objective function with suitable smoothness properties (e.g. Differentiable function, differentiable or Subderivative, subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high Computational complexity, computational burden, achieving faster iterations in exchange for a lower Rate of convergence, convergence rate. The basic idea behind stochastic approximation can be traced back to the Robbins–Monro algorithm of the 1950s. Today, stochastic gradient descent has become an important optimization method in machine learning. Background Both statistics, statistical M-estimation, estimation and ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Aryeh Dvoretzky
Aryeh (Arie) Dvoretzky (, ; May 3, 1916 – May 8, 2008) was a Ukrainian-born Israeli mathematician, the winner of the 1973 Israel Prize in Mathematics. He is best known for his work in functional analysis, statistics and probability. He was the eighth president of the Weizmann Institute of Science. Biography Aryeh Dvoretzky was born in Khorol, Imperial Russia (now Ukraine). His family immigrated to Palestine in 1922. He graduated from the Hebrew Reali School in Haifa in 1933, and received his Ph.D. at the Hebrew University of Jerusalem in 1941. His advisor was Michael Fekete. He continued working in Jerusalem, becoming a full professor in 1951, the first graduate of the Hebrew University to achieve this distinction. Dvoretzky's son Gideon was killed in the 1973 Yom Kippur War. Academic career Dvoretzky had visiting appointments at a number of universities, including Collège de France, Columbia University, Purdue University, Stanford University, and the University of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Estimation
Estimation (or estimating) is the process of finding an estimate or approximation, which is a value that is usable for some purpose even if input data may be incomplete, uncertain, or unstable. The value is nonetheless usable because it is derived from the best information available.C. Lon Enloe, Elizabeth Garnett, Jonathan Miles, ''Physical Science: What the Technology Professional Needs to Know'' (2000), p. 47. Typically, estimation involves "using the value of a statistic derived from a sample to estimate the value of a corresponding population parameter".Raymond A. Kent, "Estimation", ''Data Construction and Data Analysis for Survey Research'' (2001), p. 157. The sample provides information that can be projected, through various formal or informal processes, to determine a range most likely to describe the missing information. An estimate that turns out to be incorrect will be an overestimate if the estimate exceeds the actual result and an underestimate if the estimate f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Robust Statistics
Robust statistics are statistics that maintain their properties even if the underlying distributional assumptions are incorrect. Robust Statistics, statistical methods have been developed for many common problems, such as estimating location parameter, location, scale parameter, scale, and regression coefficient, regression parameters. One motivation is to produce statistical methods that are not unduly affected by outliers. Another motivation is to provide methods with good performance when there are small departures from a Parametric statistics, parametric distribution. For example, robust methods work well for mixtures of two normal distributions with different standard deviations; under this model, non-robust methods like a t-test work poorly. Introduction Robust statistics seek to provide methods that emulate popular statistical methods, but are not unduly affected by outliers or other small departures from Statistical assumption, model assumptions. In statistics, classical e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Control Theory
Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control Stability theory, stability; often with the aim to achieve a degree of Optimal control, optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or Setpoint (control system), set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Simultaneous Perturbation Stochastic Approximation
Simultaneous perturbation stochastic approximation (SPSA) is an algorithmic method for optimizing systems with multiple unknown parameters. It is a type of stochastic approximation algorithm. As an optimization method, it is appropriately suited to large-scale population models, adaptive modeling, simulation optimization, and atmospheric modeling. Many examples are presented at the SPSA website http://www.jhuapl.edu/SPSA. A comprehensive book on the subject is Bhatnagar et al. (2013). An early paper on the subject is Spall (1987) and the foundational paper providing the key theory and justification is Spall (1992). SPSA is a descent method capable of finding global minima, sharing this property with other methods such as simulated annealing. Its main feature is the gradient approximation that requires only two measurements of the objective function, regardless of the dimension of the optimization problem. Recall that we want to find the optimal control u^* with loss function J(u): ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Finite Difference
A finite difference is a mathematical expression of the form . Finite differences (or the associated difference quotients) are often used as approximations of derivatives, such as in numerical differentiation. The difference operator, commonly denoted \Delta, is the operator (mathematics), operator that maps a function to the function \Delta[f] defined by \Delta[f](x) = f(x+1)-f(x). A difference equation is a functional equation that involves the finite difference operator in the same way as a differential equation involves derivatives. There are many similarities between difference equations and differential equations. Certain Recurrence relation#Relationship to difference equations narrowly defined, recurrence relations can be written as difference equations by replacing iteration notation with finite differences. In numerical analysis, finite differences are widely used for #Relation with derivatives, approximating derivatives, and the term "finite difference" is often used a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Jacob Wolfowitz
Jacob Wolfowitz (March 19, 1910 – July 16, 1981) was a Polish-born American Jewish statistician and Shannon Award-winning information theorist. He was the father of former United States Deputy Secretary of Defense and World Bank Group President Paul Wolfowitz. Early life and education Wolfowitz was born in 1910 in Warsaw, Poland, the son of Helen (Pearlman) and Samuel Wolfowitz. He emigrated with his parents to the United States in 1920. He received a bachelor of science in 1931 from the City College of New York. Career In the mid-1930s, Wolfowitz began his career as a high school mathematics teacher and continued teaching until 1942 when he received his Ph.D. degree in mathematics from New York University. While a part-time graduate student, Wolfowitz met Abraham Wald, with whom he collaborated in numerous joint papers in the field of mathematical statistics. This collaboration continued until Wald's death in an airplane crash in 1950. In 1951, Wolfowitz became a professor o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |