stochastic gradient descent

Stochastic gradient descent (often abbreviated SGD) is an iterative method for optimizing an objective function with suitable smoothness properties (e.g. differentiable or subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high computational burden, achieving faster iterations in exchange for a lower convergence rate.

The basic idea behind stochastic approximation can be traced back to the Robbins–Monro algorithm of the 1950s. Today, stochastic gradient descent has become an important optimization method in machine learning.

Background

Both statistical estimation and machine learning consider the problem of minimizing an objective function that has the form of a sum:
$Q(w) = \frac\sum_^n Q_i(w),$
where the parameter $w$ that minimizes $Q(w)$ is to be estimated. Each summand function $Q_i$ is typically associated with the $i$-th observation in the data set (used for training).

In classical statistics, sum-minimization problems arise in least squares and in maximum-likelihood estimation (for independent observations). The general class of estimators that arise as minimizers of sums are called M-estimators. However, in statistics, it has been long recognized that requiring even local minimization is too restrictive for some problems of maximum-likelihood estimation. Therefore, contemporary statistical theorists often consider stationary points of the likelihood function (or zeros of its derivative, the score function, and other estimating equations).

The sum-minimization problem also arises for empirical risk minimization. There, $Q_i(w)$ is the value of the loss function at $i$-th example, and $Q(w)$ is the empirical risk.

When used to minimize the above function, a standard (or "batch") gradient descent method would perform the following iterations:
$w := w - \eta\,\nabla Q(w) = w - \frac \sum_^n \nabla Q_i(w).$
The step size is denoted by $\eta$ (sometimes called the ''learning rate'' in machine learning) and here "$:=$" denotes the update of a variable in the algorithm.

In many cases, the summand functions have a simple form that enables inexpensive evaluations of the sum-function and the sum gradient. For example, in statistics, one-parameter exponential families allow economical function-evaluations and gradient-evaluations.

However, in other cases, evaluating the sum-gradient may require expensive evaluations of the gradients from all summand functions. When the training set is enormous and no simple formulas exist, evaluating the sums of gradients becomes very expensive, because evaluating the gradient requires evaluating all the summand functions' gradients. To economize on the computational cost at every iteration, stochastic gradient descent samples a subset of summand functions at every step. This is very effective in the case of large-scale machine learning problems.

Iterative method

In stochastic (or "on-line") gradient descent, the true gradient of $Q(w)$ is approximated by a gradient at a single sample:
$w := w - \eta\, \nabla Q_i(w).$
As the algorithm sweeps through the training set, it performs the above update for each training sample. Several passes can be made over the training set until the algorithm converges. If this is done, the data can be shuffled for each pass to prevent cycles. Typical implementations may use an adaptive learning rate so that the algorithm converges.

In pseudocode, stochastic gradient descent can be presented as :

* Choose an initial vector of parameters $w$ and learning rate $\eta$.
* Repeat until an approximate minimum is obtained:
** Randomly shuffle samples in the training set.
** For $i=1, 2, ..., n$, do:
*** $w := w - \eta\, \nabla Q_i(w).$

A compromise between computing the true gradient and the gradient at a single sample is to compute the gradient against more than one training sample (called a "mini-batch") at each step. This can perform significantly better than "true" stochastic gradient descent described, because the code can make use of vectorization libraries rather than computing each step separately as was first shown in where it was called "the bunch-mode back-propagation algorithm". It may also result in smoother convergence, as the gradient computed at each step is averaged over more training samples.

The convergence of stochastic gradient descent has been analyzed using the theories of convex minimization and of stochastic approximation. Briefly, when the learning rates $\eta$ decrease with an appropriate rate,
and subject to relatively mild assumptions, stochastic gradient descent converges almost surely to a global minimum
when the objective function is convex or pseudoconvex,
and otherwise converges almost surely to a local minimum.
This is in fact a consequence of the Robbins–Siegmund theorem.

Linear regression

Suppose we want to fit a straight line $\hat y = w_1 + w_2 x$ to a training set with observations $((x_1, y_1), (x_2, y_2) \ldots, (x_n, y_n))$ and corresponding estimated responses $(\hat y_1, \hat y_2, \ldots, \hat y_n)$ using least squares. The objective function to be minimized is
$Q(w) = \sum_^n Q_i(w) = \sum_^n \left(\hat y_i - y_i\right)^2 = \sum_^n \left(w_1 + w_2 x_i - y_i\right)^2.$
The last line in the above pseudocode for this specific problem will become:
$\begin w_1 \\ w_2 \end \leftarrow \begin w_1 \\ w_2 \end - \eta \begin \frac (w_1 + w_2 x_i - y_i)^2 \\ \frac (w_1 + w_2 x_i - y_i)^2 \end = \begin w_1 \\ w_2 \end - \eta \begin 2 (w_1 + w_2 x_i - y_i) \\ 2 x_i(w_1 + w_2 x_i - y_i) \end.$Note that in each iteration or update step, the gradient is only evaluated at a single $x_i$. This is the key difference between stochastic gradient descent and batched gradient descent.

In general, given a linear regression $\hat y = \sum_ w_k x_k$ problem, stochastic gradient descent behaves differently when $m < n$ (underparameterized) and $m \geq n$ (overparameterized). In the overparameterized case, stochastic gradient descent converges to $\arg\min_ \, w - w_0\,$. That is, SGD converges to the interpolation solution with minimum distance from the starting $w_0$. This is true even when the learning rate remains constant. In the underparameterized case, SGD does not converge if learning rate remains constant.

History

In 1951, Herbert Robbins and Sutton Monro introduced the earliest stochastic approximation methods, preceding stochastic gradient descent. Building on this work one year later, Jack Kiefer and Jacob Wolfowitz published an optimization algorithm very close to stochastic gradient descent, using central differences as an approximation of the gradient. Later in the 1950s, Frank Rosenblatt used SGD to optimize his perceptron model, demonstrating the first applicability of stochastic gradient descent to neural networks.

Backpropagation was first described in 1986, with stochastic gradient descent being used to efficiently optimize parameters across neural networks with multiple hidden layers. Soon after, another improvement was developed: mini-batch gradient descent, where small batches of data are substituted for single samples. In 1997, the practical performance benefits from vectorization achievable with such small batches were first explored, paving the way for efficient optimization in machine learning. As of 2023, this mini-batch approach remains the norm for training neural networks, balancing the benefits of stochastic gradient descent with gradient descent.

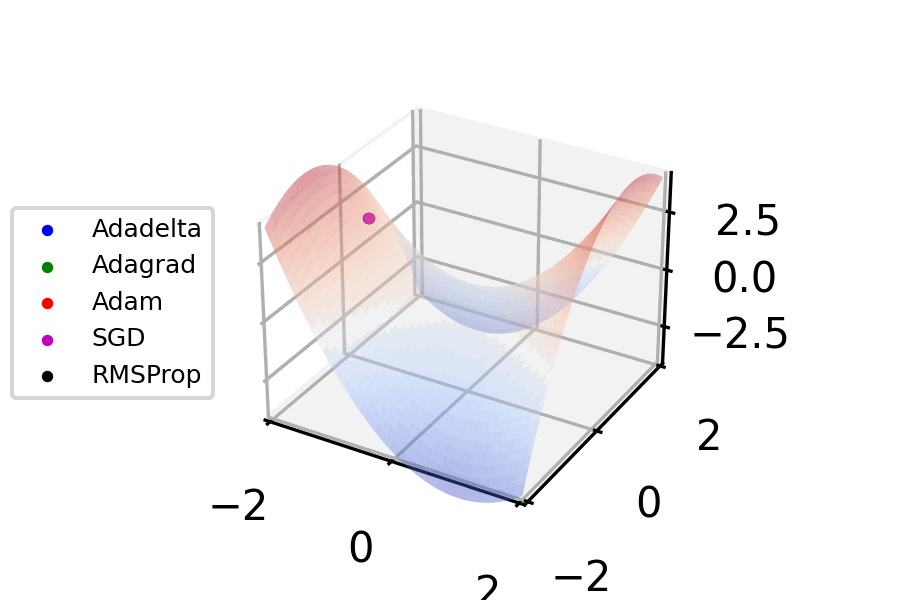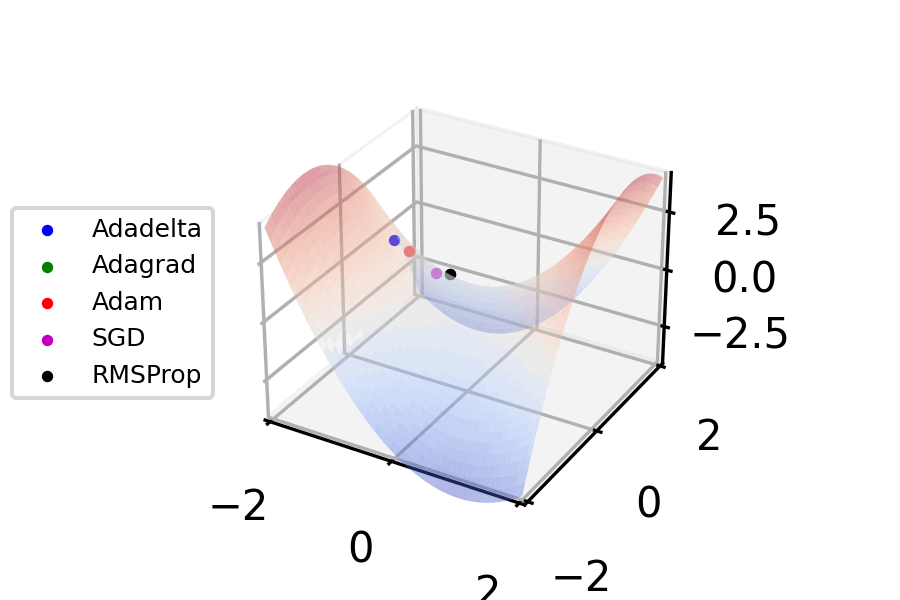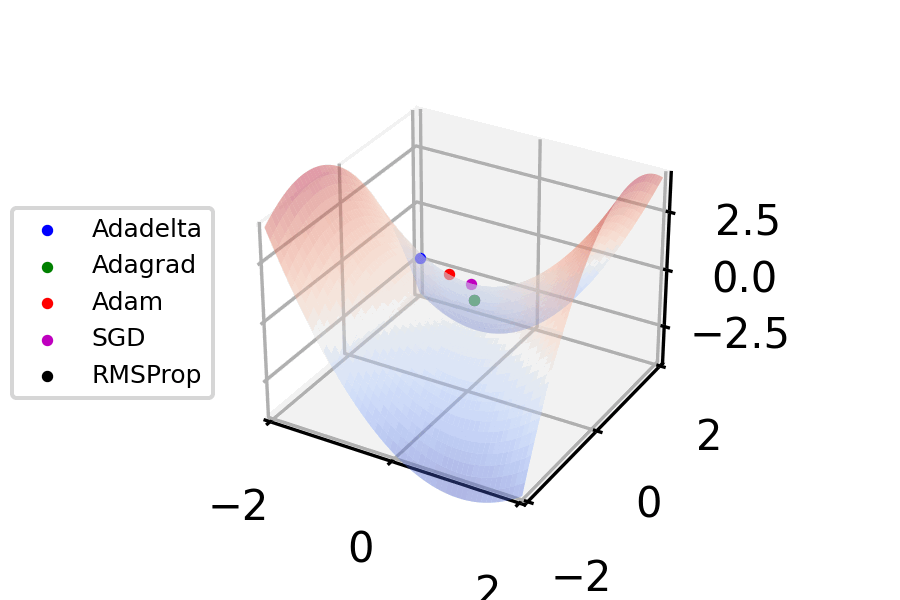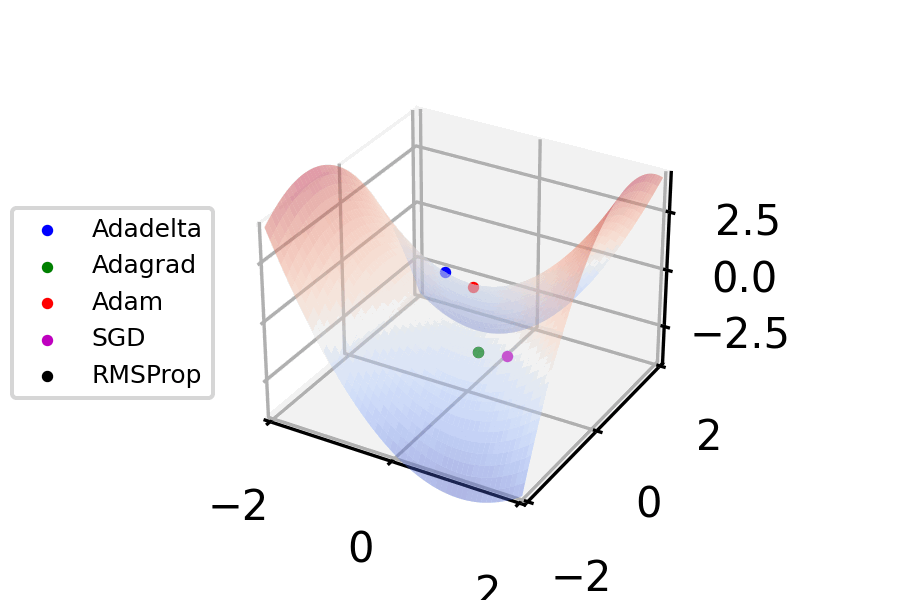
By the 1980s, momentum had already been introduced, and was added to SGD optimization techniques in 1986. However, these optimization techniques assumed constant hyperparameters, i.e. a fixed learning rate and momentum parameter. In the 2010s, adaptive approaches to applying SGD with a per-parameter learning rate were introduced with AdaGrad (for "Adaptive Gradient") in 2011 and RMSprop (for "Root Mean Square Propagation") in 2012. In 2014, Adam (for "Adaptive Moment Estimation") was published, applying the adaptive approaches of RMSprop to momentum; many improvements and branches of Adam were then developed such as Adadelta, Adagrad, AdamW, and Adamax.

Within machine learning, approaches to optimization in 2023 are dominated by Adam-derived optimizers. TensorFlow and PyTorch, by far the most popular machine learning libraries, as of 2023 largely only include Adam-derived optimizers, as well as predecessors to Adam such as RMSprop and classic SGD. PyTorch also partially supports Limited-memory BFGS, a line-search method, but only for single-device setups without parameter groups.

Notable applications

Stochastic gradient descent is a popular algorithm for training a wide range of models in machine learning, including (linear) support vector machines, logistic regression (see, e.g., Vowpal Wabbit) and graphical models. When combined with the back propagation algorithm, it is the ''de facto'' standard algorithm for training artificial neural networks. Its use has been also reported in the Geophysics community, specifically to applications of Full Waveform Inversion (FWI).

Stochastic gradient descent competes with the L-BFGS algorithm, which is also widely used. Stochastic gradient descent has been used since at least 1960 for training linear regression models, originally under the name ADALINE.

Another stochastic gradient descent algorithm is the least mean squares (LMS) adaptive filter.

Extensions and variants

Many improvements on the basic stochastic gradient descent algorithm have been proposed and used. In particular, in machine learning, the need to set a learning rate (step size) has been recognized as problematic. Setting this parameter too high can cause the algorithm to diverge; setting it too low makes it slow to converge. A conceptually simple extension of stochastic gradient descent makes the learning rate a decreasing function of the iteration number , giving a ''learning rate schedule'', so that the first iterations cause large changes in the parameters, while the later ones do only fine-tuning. Such schedules have been known since the work of MacQueen on -means clustering. Practical guidance on choosing the step size in several variants of SGD is given by Spall.

Implicit updates (ISGD)

As mentioned earlier, classical stochastic gradient descent is generally sensitive to learning rate . Fast convergence requires large learning rates but this may induce numerical instability. The problem can be largely solved by considering ''implicit updates'' whereby the stochastic gradient is evaluated at the next iterate rather than the current one:
$w^\text := w^\text - \eta\, \nabla Q_i(w^\text).$

This equation is implicit since $w^\text$ appears on both sides of the equation. It is a stochastic form of the proximal gradient method since the update
can also be written as:
$w^\text := \arg\min_w \left\.$

As an example,
consider least squares with features $x_1, \ldots, x_n \in\mathbb^p$ and observations
$y_1, \ldots, y_n\in\mathbb$. We wish to solve:
$\min_w \sum_^n \left(y_j - x_j'w\right)^2,$
where $x_j' w = x_ w_1 + x_ w_2 + ... + x_ w_p$ indicates the inner product.
Note that $x$ could have "1" as the first element to include an intercept. Classical stochastic gradient descent proceeds as follows:
$w^\text = w^\text + \eta \left(y_i - x_i'w^\text\right) x_i$

where $i$ is uniformly sampled between 1 and $n$. Although theoretical convergence of this procedure happens under relatively mild assumptions, in practice the procedure can be quite unstable. In particular, when $\eta$ is misspecified so that $I - \eta x_i x_i'$ has large absolute eigenvalues with high probability, the procedure may diverge numerically within a few iterations. In contrast, ''implicit stochastic gradient descent'' (shortened as ISGD) can be solved in closed-form as:
$w^\text = w^\text + \frac \left(y_i - x_i'w^\text\right) x_i.$

This procedure will remain numerically stable virtually for all $\eta$ as the learning rate is now normalized. Such comparison between classical and implicit stochastic gradient descent in the least squares problem is very similar to the comparison between least mean squares (LMS) and
normalized least mean squares filter (NLMS).

Even though a closed-form solution for ISGD is only possible in least squares, the procedure can be efficiently implemented in a wide range of models. Specifically, suppose that $Q_i(w)$ depends on $w$ only through a linear combination with features $x_i$, so that we can write $\nabla_w Q_i(w) = -q(x_i'w) x_i$, where $q() \in\mathbb$ may depend on $x_i, y_i$ as well but not on $w$ except through $x_i'w$. Least squares obeys this rule, and so does logistic regression, and most generalized linear models. For instance, in least squares, $q(x_i'w) = y_i - x_i'w$, and in logistic regression $q(x_i'w) = y_i - S(x_i'w)$, where $S(u) = e^u/(1+e^u)$ is the logistic function. In Poisson regression, $q(x_i'w) = y_i - e^$, and so on.

In such settings, ISGD is simply implemented as follows. Let $f(\xi) = \eta q(x_i'w^\text + \xi \, x_i\, ^2)$, where $\xi$ is scalar.
Then, ISGD is equivalent to:
$w^\text = w^\text + \xi^\ast x_i,~\text~\xi^\ast = f(\xi^\ast).$

The scaling factor $\xi^\ast\in\mathbb$ can be found through the bisection method since in most regular models, such as the aforementioned generalized linear models, function $q()$ is decreasing, and thus the search bounds for $\xi^\ast$ are min(0, f(0)), \max(0, f(0))/math>.

Momentum

Further proposals include the ''momentum method'' or the ''heavy ball method'', which in ML context appeared in Rumelhart, Hinton and Williams' paper on backpropagation learning and borrowed the idea from Soviet mathematician Boris Polyak's 1964 article on solving functional equations. Stochastic gradient descent with momentum remembers the update at each iteration, and determines the next update as a linear combination of the gradient and the previous update:
$\Delta w := \alpha \Delta w - \eta\, \nabla Q_i(w)$
$w := w + \Delta w$
that leads to:
$w := w - \eta\, \nabla Q_i(w) + \alpha \Delta w$

where the parameter $w$ which minimizes $Q(w)$ is to be estimated, $\eta$ is a step size (sometimes called the ''learning rate'' in machine learning) and $\alpha$ is an exponential decay factor between 0 and 1 that determines the relative contribution of the current gradient and earlier gradients to the weight change.

The name momentum stems from an analogy to momentum in physics: the weight vector $w$, thought of as a particle traveling through parameter space, incurs acceleration from the gradient of the loss ("force"). Unlike in classical stochastic gradient descent, it tends to keep traveling in the same direction, preventing oscillations. Momentum has been used successfully by computer scientists in the training of artificial neural networks for several decades.
The ''momentum method'' is closely related to underdamped Langevin dynamics, and may be combined with simulated annealing.

In mid-1980s the method was modified by Yurii Nesterov to use the gradient predicted at the next point, and the resulting so-called ''Nesterov Accelerated Gradient'' was sometimes used in ML in the 2010s.

Averaging

''Averaged stochastic gradient descent'', invented independently by Ruppert and Polyak in the late 1980s, is ordinary stochastic gradient descent that records an average of its parameter vector over time. That is, the update is the same as for ordinary stochastic gradient descent, but the algorithm also keeps track of

$\bar = \frac \sum_^ w_i.$When optimization is done, this averaged parameter vector takes the place of .

AdaGrad

''AdaGrad'' (for adaptive gradient algorithm) is a modified stochastic gradient descent algorithm with per-parameter learning rate, first published in 2011. Informally, this increases the learning rate for and decreases the learning rate for ones that are less sparse. This strategy often improves convergence performance over standard stochastic gradient descent in settings where data is sparse and sparse parameters are more informative. Examples of such applications include natural language processing and image recognition.

It still has a base learning rate , but this is multiplied with the elements of a vector which is the diagonal of the outer product matrix

$G = \sum_^t g_\tau g_\tau^\mathsf$

where $g_\tau = \nabla Q_i(w)$, the gradient, at iteration . The diagonal is given by

$G_ = \sum_^t g_^2.$This vector essentially stores a historical sum of gradient squares by dimension and is updated after every iteration. The formula for an update is now
$w := w - \eta\, \mathrm(G)^ \odot g$
or, written as per-parameter updates,
$w_j := w_j - \frac g_j.$
Each gives rise to a scaling factor for the learning rate that applies to a single parameter . Since the denominator in this factor, $\sqrt = \sqrt$ is the ''ℓ''₂ norm of previous derivatives, extreme parameter updates get dampened, while parameters that get few or small updates receive higher learning rates.

While designed for convex problems, AdaGrad has been successfully applied to non-convex optimization.

RMSProp

''RMSProp'' (for Root Mean Square Propagation) is a method invented in 2012 by James Martens and Ilya Sutskever, at the time both PhD students in Geoffrey Hinton's group, in which the learning rate is, like in Adagrad, adapted for each of the parameters. The idea is to divide the learning rate for a weight by a running average of the magnitudes of recent gradients for that weight. Unusually, it was not published in an article but merely described in a Coursera lecture.

So, first the running average is calculated in terms of means square,

$v(w,t):=\gamma v(w,t-1) + \left(1-\gamma\right) \left(\nabla Q_i(w)\right)^2$

where, $\gamma$ is the forgetting factor. The concept of storing the historical gradient as sum of squares is borrowed from Adagrad, but "forgetting" is introduced to solve Adagrad's diminishing learning rates in non-convex problems by gradually decreasing the influence of old data.

And the parameters are updated as,

$w:=w-\frac\nabla Q_i(w)$

RMSProp has shown good adaptation of learning rate in different applications. RMSProp can be seen as a generalization of Rprop and is capable to work with mini-batches as well opposed to only full-batches.

Adam

''Adam'' (short for Adaptive Moment Estimation) is a 2014 update to the ''RMSProp'' optimizer combining it with the main feature of the ''Momentum method''. In this optimization algorithm, running averages with exponential forgetting of both the gradients and the second moments of the gradients are used. Given parameters $w^$ and a loss function $L ^$, where $t$ indexes the current training iteration (indexed at $1$), Adam's parameter update is given by:

$m_w ^ := \beta_1 m_w ^ + \left(1 - \beta_1\right) \nabla _w L ^$
$v_w ^ := \beta_2 v_w ^ + \left(1 - \beta_2\right) \left(\nabla _w L ^ \right)^2$

$\hat_w ^ = \frac$
$\hat_w ^ = \frac$

$w ^ := w ^ - \eta \frac$
where $\varepsilon$ is a small scalar (e.g. $10^$) used to prevent division by 0, and $\beta_1$ (e.g. 0.9) and $\beta_2$ (e.g. 0.999) are the forgetting factors for gradients and second moments of gradients, respectively. Squaring and square-rooting is done element-wise.

As the exponential moving averages of the gradient $m_w ^$ and the squared gradient $v_w ^$ are initialized with a vector of 0's, there would be a bias towards zero in the first training iterations. A factor $\tfrac$ is introduced to compensate this bias and get better estimates $\hat_w ^$ and $\hat_w ^$.

The initial proof establishing the convergence of Adam was incomplete, and subsequent analysis has revealed that Adam does not converge for all convex objectives. Despite this, ''Adam'' continues to be used due to its strong performance in practice.

Variants

The popularity of ''Adam'' inspired many variants and enhancements. Some examples include:

* Nesterov-enhanced gradients: ''NAdam'', ''FASFA''
* varying interpretations of second-order information: ''Powerpropagation'' and ''AdaSqrt''.
* Using infinity norm: ''AdaMax''
* ''AMSGrad'', which improves convergence over ''Adam'' by using maximum of past squared gradients instead of the exponential average. ''AdamX'' further improves convergence over ''AMSGrad''.
* ''AdamW'', which improves the weight decay.

Sign-based stochastic gradient descent

Even though sign-based optimization goes back to the aforementioned ''Rprop'', in 2018 researchers tried to simplify Adam by removing the magnitude of the stochastic gradient from being taken into account and only considering its sign.

Backtracking line search

Backtracking line search is another variant of gradient descent. All of the below are sourced from the mentioned link. It is based on a condition known as the Armijo–Goldstein condition. Both methods allow learning rates to change at each iteration; however, the manner of the change is different. Backtracking line search uses function evaluations to check Armijo's condition, and in principle the loop in the algorithm for determining the learning rates can be long and unknown in advance. Adaptive SGD does not need a loop in determining learning rates. On the other hand, adaptive SGD does not guarantee the "descent property" – which Backtracking line search enjoys – which is that $f(x_)\leq f(x_n)$ for all n. If the gradient of the cost function is globally Lipschitz continuous, with Lipschitz constant L, and learning rate is chosen of the order 1/L, then the standard version of SGD is a special case of backtracking line search.

Second-order methods

A stochastic analogue of the standard (deterministic) Newton–Raphson algorithm (a "second-order" method) provides an asymptotically optimal or near-optimal form of iterative optimization in the setting of stochastic approximation. A method that uses direct measurements of the Hessian matrices of the summands in the empirical risk function was developed by Byrd, Hansen, Nocedal, and Singer. However, directly determining the required Hessian matrices for optimization may not be possible in practice. Practical and theoretically sound methods for second-order versions of SGD that do not require direct Hessian information are given by Spall and others. (A less efficient method based on finite differences, instead of simultaneous perturbations, is given by Ruppert.) Another approach to the approximation Hessian matrix is replacing it with the Fisher information matrix, which transforms usual gradient to natural. These methods not requiring direct Hessian information are based on either values of the summands in the above empirical risk function or values of the gradients of the summands (i.e., the SGD inputs). In particular, second-order optimality is asymptotically achievable without direct calculation of the Hessian matrices of the summands in the empirical risk function. When the objective is a nonlinear least-squres loss
$Q(w) = \frac \sum_^n Q_i(w) = \frac \sum_^n (m(w;x_i)-y_i)^2,$
where $m(w;x_i)$ is the predictive model (e.g., a deep neural network)
the objective's structure can be exploited to estimate 2nd order information using gradients only. The resulting
methods are simple and often effective

Approximations in continuous time

For small learning rate $\eta$ stochastic gradient descent $(w_n)_$ can be viewed as a discretization of the gradient flow ODE

$\frac W_t = -\nabla Q(W_t)$

subject to additional stochastic noise. This approximation is only valid on a finite time-horizon in the following sense: assume that all the coefficients $Q_i$ are sufficiently smooth. Let $T >0$ and $g: \R^d \to \R$ be a sufficiently smooth test function. Then, there exists a constant $C>0$ such that for all $\eta >0$

\max_ \left, \mathbb E (w_k)g(W_)\ \le C \eta,

where $\mathbb E$ denotes taking the expectation with respect to the random choice of indices in the stochastic gradient descent scheme.

Since this approximation does not capture the random fluctuations around the mean behavior of stochastic gradient descent solutions to stochastic differential equations (SDEs) have been proposed as limiting objects. More precisely, the solution to the SDE

$d W_t = - \nabla \left(Q(W_t)+\tfrac 1 4 \eta , \nabla Q(W_t), ^2\right)dt + \sqrt \eta \Sigma (W_t)^ dB_t,$

for $\Sigma(w) = \frac \left(\sum_^n Q_i(w)-Q(w)\right)\left(\sum_^n Q_i(w)-Q(w)\right)^T$ where $dB_t$ denotes the Ito-integral with respect to a Brownian motion is a more precise approximation in the sense that there exists a constant $C>0$ such that

\max_ \left, \mathbb E (w_k)\mathbb E (W_) \le C \eta^2.

However this SDE only approximates the one-point motion of stochastic gradient descent. For an approximation of the stochastic flow one has to consider SDEs with infinite-dimensional noise.

See also

*Backtracking line search
*Broken Neural Scaling Law
* Coordinate descent – changes one coordinate at a time, rather than one example
* Linear classifier
* Online machine learning
* Stochastic hill climbing
* Stochastic variance reduction

Notes

References

Further reading

*
*
*
*

External links

*
* Interactive paper explaining momentum.

{{Artificial intelligence navbox

Stochastic optimization
Computational statistics
Gradient methods
M-estimators
Machine learning algorithms
Convex optimization
Statistical approximations