|
Limited-memory BFGS
Limited-memory BFGS (L-BFGS or LM-BFGS) is an optimization algorithm in the family of quasi-Newton methods that approximates the Broyden–Fletcher–Goldfarb–Shanno algorithm (BFGS) using a limited amount of computer memory. It is a popular algorithm for parameter estimation in machine learning. The algorithm's target problem is to minimize f(\mathbf) over unconstrained values of the real-vector \mathbf where f is a differentiable scalar function. Like the original BFGS, L-BFGS uses an estimate of the inverse Hessian matrix to steer its search through variable space, but where BFGS stores a dense n\times n approximation to the inverse Hessian (''n'' being the number of variables in the problem), L-BFGS stores only a few vectors that represent the approximation implicitly. Due to its resulting linear memory requirement, the L-BFGS method is particularly well suited for optimization problems with many variables. Instead of the inverse Hessian H''k'', L-BFGS maintains a history of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization (mathematics)
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Function
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in its domain. A differentiable function is smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, is said to be of class if its first k derivatives f^(x), f^(x), \ldots, f^(x) exist and are continuous over the domain of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SciPy
SciPy (pronounced "sigh pie") is a free and open-source Python library used for scientific computing and technical computing. SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, fast Fourier transform, signal and image processing, ordinary differential equation solvers and other tasks common in science and engineering. SciPy is also a family of conferences for users and developers of these tools: SciPy (in the United States), EuroSciPy (in Europe) and SciPy.in (in India). Enthought originated the SciPy conference in the United States and continues to sponsor many of the international conferences as well as host the SciPy website. The SciPy library is currently distributed under the BSD license, and its development is sponsored and supported by an open community of developers. It is also supported by NumFOCUS, a community foundation for supporting reproducible and accessible science. Components The SciPy package is at the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
R (programming Language)
R is a programming language for statistical computing and Data and information visualization, data visualization. It has been widely adopted in the fields of data mining, bioinformatics, data analysis, and data science. The core R language is extended by a large number of R package, software packages, which contain Reusability, reusable code, documentation, and sample data. Some of the most popular R packages are in the tidyverse collection, which enhances functionality for visualizing, transforming, and modelling data, as well as improves the ease of programming (according to the authors and users). R is free and open-source software distributed under the GNU General Public License. The language is implemented primarily in C (programming language), C, Fortran, and Self-hosting (compilers), R itself. Preprocessor, Precompiled executables are available for the major operating systems (including Linux, MacOS, and Microsoft Windows). Its core is an interpreted language with a na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ALGLIB
ALGLIB is a cross-platform open source numerical analysis and data processing library. It can be used from several programming languages ( C++, C#, VB.NET, Python, Delphi, Java). ALGLIB started in 1999 and has a long history of steady development with roughly 1-3 releases per year. It is used by several open-source projects, commercial libraries, and applications (e.g. TOL project, Math.NET Numerics, SpaceClaim). Features Distinctive features of the library are: * Support for several programming languages with identical APIs (as of 2023, it supports C++, C#, FreePascal/Delphi, VB.NET, Python, and Java) * Self-contained code with no mandatory external dependencies and easy installation * Portability (it was tested under x86/x86-64/ARM, Windows and Linux) * Two independent backends (pure C# implementation, native C implementation) with automatically generated APIs (C++, C#, ...) * Same functionality of commercial and GPL versions, with enhancements for speed and parallelism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a function \mathrm: \mathbb \to \mathbb defined as: \operatorname z = \frac\int_0^z e^\,\mathrm dt. The integral here is a complex Contour integration, contour integral which is path-independent because \exp(-t^2) is Holomorphic function, holomorphic on the whole complex plane \mathbb. In many applications, the function argument is a real number, in which case the function value is also real. In some old texts, the error function is defined without the factor of \frac. This nonelementary integral is a sigmoid function, sigmoid function that occurs often in probability, statistics, and partial differential equations. In statistics, for non-negative real values of , the error function has the following interpretation: for a real random variable that is normal distribution, normally distributed with mean 0 and standard deviation \frac, is the probability that falls in the range . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Gradient Descent
Stochastic gradient descent (often abbreviated SGD) is an Iterative method, iterative method for optimizing an objective function with suitable smoothness properties (e.g. Differentiable function, differentiable or Subderivative, subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high Computational complexity, computational burden, achieving faster iterations in exchange for a lower Rate of convergence, convergence rate. The basic idea behind stochastic approximation can be traced back to the Robbins–Monro algorithm of the 1950s. Today, stochastic gradient descent has become an important optimization method in machine learning. Background Both statistics, statistical M-estimation, estimation and ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Online Machine Learning
In computer science, online machine learning is a method of machine learning in which data becomes available in a sequential order and is used to update the best predictor for future data at each step, as opposed to batch learning techniques which generate the best predictor by learning on the entire training data set at once. Online learning is a common technique used in areas of machine learning where it is computationally infeasible to train over the entire dataset, requiring the need of out-of-core algorithms. It is also used in situations where it is necessary for the algorithm to dynamically adapt to new patterns in the data, or when the data itself is generated as a function of time, e.g., prediction of prices in the financial international markets. Online learning algorithms may be prone to catastrophic interference, a problem that can be addressed by incremental learning approaches. Introduction In the setting of supervised learning, a function of f : X \to Y is to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign (mathematics)
In mathematics, the sign of a real number is its property of being either positive, negative, or 0. Depending on local conventions, zero may be considered as having its own unique sign, having no sign, or having both positive and negative sign. In some contexts, it makes sense to distinguish between a positive and a negative zero. In mathematics and physics, the phrase "change of sign" is associated with exchanging an object for its additive inverse (multiplication with −1, negation), an operation which is not restricted to real numbers. It applies among other objects to vectors, matrices, and complex numbers, which are not prescribed to be only either positive, negative, or zero. The word "sign" is also often used to indicate binary aspects of mathematical or scientific objects, such as odd and even ( sign of a permutation), sense of orientation or rotation ( cw/ccw), one sided limits, and other concepts described in below. Sign of a number Numbers from various number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
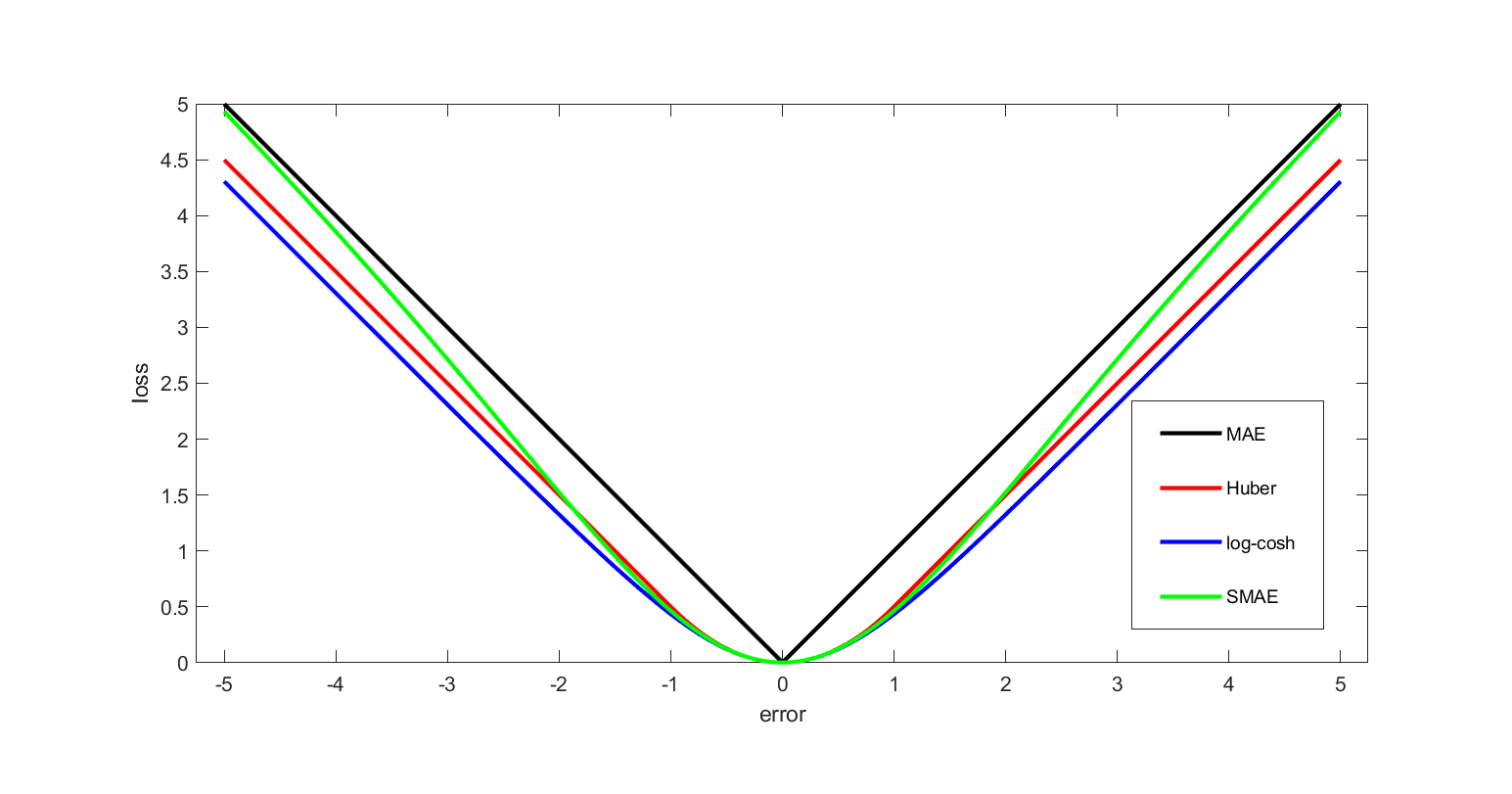
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Function
In mathematics, a real-valued function is called convex if the line segment between any two distinct points on the graph of a function, graph of the function lies above or on the graph between the two points. Equivalently, a function is convex if its epigraph (mathematics), ''epigraph'' (the set of points on or above the graph of the function) is a convex set. In simple terms, a convex function graph is shaped like a cup \cup (or a straight line like a linear function), while a concave function's graph is shaped like a cap \cap. A twice-differentiable function, differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain of a function, domain. Well-known examples of convex functions of a single variable include a linear function f(x) = cx (where c is a real number), a quadratic function cx^2 (c as a nonnegative real number) and an exponential function ce^x (c as a nonnegative real number). Convex functions pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements (e.g., ''m'' × ''n'' for an ''m'' × ''n'' matrix) is sometimes referred to as the sparsity of the matrix. Conceptually, sparsity corresponds to systems with few pairwise interactions. For example, consider a line of balls connected by springs from one to the next: this is a sparse system, as only adjacent balls are coupled. By contrast, if the same line of balls were to have springs connecting each ball to all other balls, the system would correspond to a dense matrix. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |