Fractal Sparks

In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.

One way that fractals are different from finite geometric figures is how they scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon). Likewise, if the radius of a filled sphere is doubled, its volume scales by eight, which is two (the ratio of the new to the old radius) to the power of three (the conventional dimension of the filled sphere). However, if a fractal's one-dimensional lengths are all doubled, the spatial content of the fractal scales by a power that is not necessarily an integer and is in general greater than its conventional dimension. This power is called the fractal dimension of the geometric object, to distinguish it from the conventional dimension (which is formally called the topological dimension).

Analytically, many fractals are nowhere differentiable. An infinite fractal curve can be conceived of as winding through space differently from an ordinary line – although it is still topologically 1-dimensional, its fractal dimension indicates that it locally fills space more efficiently than an ordinary line.

Starting in the 17th century with notions of recursion, fractals have moved through increasingly rigorous mathematical treatment to the study of continuous but not differentiable functions in the 19th century by the seminal work of Bernard Bolzano, Bernhard Riemann, and Karl Weierstrass, and on to the coining of the word ''fractal'' in the 20th century with a subsequent burgeoning of interest in fractals and computer-based modelling in the 20th century.

There is some disagreement among mathematicians about how the concept of a fractal should be formally defined. Mandelbrot himself summarized it as "beautiful, damn hard, increasingly useful. That's fractals." More formally, in 1982 Mandelbrot defined ''fractal'' as follows: "A fractal is by definition a set for which the Hausdorff–Besicovitch dimension strictly exceeds the topological dimension." Later, seeing this as too restrictive, he simplified and expanded the definition to this: "A fractal is a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole." Still later, Mandelbrot proposed "to use ''fractal'' without a pedantic definition, to use ''fractal dimension'' as a generic term applicable to ''all'' the variants".

The consensus among mathematicians is that theoretical fractals are infinitely self-similar iterated and detailed mathematical constructs, of which many examples have been formulated and studied. Fractals are not limited to geometric patterns, but can also describe processes in time. Fractal patterns with various degrees of self-similarity have been rendered or studied in visual, physical, and aural media and found in nature, technology, art, architectureOstwald, Michael J., and Vaughan, Josephine (2016) ''The Fractal Dimension of Architecture''. Birhauser, Basel. . and law. Fractals are of particular relevance in the field of chaos theory because they show up in the geometric depictions of most chaotic processes (typically either as attractors or as boundaries between basins of attraction).

Etymology

The term "fractal" was coined by the mathematician Benoît Mandelbrot in 1975. Mandelbrot based it on the Latin , meaning "broken" or "fractured", and used it to extend the concept of theoretical fractional dimensions to geometric patterns in nature.

Introduction

The word "fractal" often has different connotations for the lay public as opposed to mathematicians, where the public is more likely to be familiar with fractal art than the mathematical concept. The mathematical concept is difficult to define formally, even for mathematicians, but key features can be understood with a little mathematical background.

The feature of "self-similarity", for instance, is easily understood by analogy to zooming in with a lens or other device that zooms in on digital images to uncover finer, previously invisible, new structure. If this is done on fractals, however, no new detail appears; nothing changes and the same pattern repeats over and over, or for some fractals, nearly the same pattern reappears over and over. Self-similarity itself is not necessarily counter-intuitive (e.g., people have pondered self-similarity informally such as in the infinite regress in parallel mirrors or the homunculus, the little man inside the head of the little man inside the head ...). The difference for fractals is that the pattern reproduced must be detailed.

This idea of being detailed relates to another feature that can be understood without much mathematical background: Having a fractal dimension greater than its topological dimension, for instance, refers to how a fractal scales compared to how geometric shapes are usually perceived. A straight line, for instance, is conventionally understood to be one-dimensional; if such a figure is rep-tiled into pieces each 1/3 the length of the original, then there are always three equal pieces. A solid square is understood to be two-dimensional; if such a figure is rep-tiled into pieces each scaled down by a factor of 1/3 in both dimensions, there are a total of 3² = 9 pieces.

We see that for ordinary self-similar objects, being n-dimensional means that when it is rep-tiled into pieces each scaled down by a scale-factor of 1/''r'', there are a total of ''r''^''n'' pieces. Now, consider the Koch curve. It can be rep-tiled into four sub-copies, each scaled down by a scale-factor of 1/3. So, strictly by analogy, we can consider the "dimension" of the Koch curve as being the unique real number ''D'' that satisfies 3^''D'' = 4. This number is what mathematicians call the ''fractal dimension'' of the Koch curve; it is certainly ''not'' what is conventionally perceived as the dimension of a curve (this number is not even an integer!). In general, a key property of fractals is that the fractal dimension differs from the ''conventionally understood'' dimension (formally called the topological dimension).

This also leads to understanding a third feature, that fractals as mathematical equations are "nowhere differentiable". In a concrete sense, this means fractals cannot be measured in traditional ways. To elaborate, in trying to find the length of a wavy non-fractal curve, one could find straight segments of some measuring tool small enough to lay end to end over the waves, where the pieces could get small enough to be considered to conform to the curve in the normal manner of measuring with a tape measure. But in measuring an infinitely "wiggly" fractal curve such as the Koch snowflake, one would never find a small enough straight segment to conform to the curve, because the jagged pattern would always re-appear, at arbitrarily small scales, essentially pulling a little more of the tape measure into the total length measured each time one attempted to fit it tighter and tighter to the curve. The result is that one must need infinite tape to perfectly cover the entire curve, i.e. the snowflake has an infinite perimeter.

History

The history of fractals traces a path from chiefly theoretical studies to modern applications in computer graphics, with several notable people contributing canonical fractal forms along the way.
A common theme in traditional African architecture is the use of fractal scaling, whereby small parts of the structure tend to look similar to larger parts, such as a circular village made of circular houses.
According to Pickover, the mathematics behind fractals began to take shape in the 17th century when the mathematician and philosopher Gottfried Leibniz pondered recursive self-similarity (although he made the mistake of thinking that only the straight line was self-similar in this sense).

In his writings, Leibniz used the term "fractional exponents", but lamented that "Geometry" did not yet know of them. Indeed, according to various historical accounts, after that point few mathematicians tackled the issues and the work of those who did remained obscured largely because of resistance to such unfamiliar emerging concepts, which were sometimes referred to as mathematical "monsters". Thus, it was not until two centuries had passed that on July 18, 1872 Karl Weierstrass presented the first definition of a function with a graph that would today be considered a fractal, having the non-intuitive property of being everywhere continuous but nowhere differentiable at the Royal Prussian Academy of Sciences.

In addition, the quotient difference becomes arbitrarily large as the summation index increases. Not long after that, in 1883, Georg Cantor, who attended lectures by Weierstrass, published examples of subsets of the real line known as Cantor sets, which had unusual properties and are now recognized as fractals. Also in the last part of that century, Felix Klein and Henri Poincaré introduced a category of fractal that has come to be called "self-inverse" fractals.

One of the next milestones came in 1904, when Helge von Koch, extending ideas of Poincaré and dissatisfied with Weierstrass's abstract and analytic definition, gave a more geometric definition including hand-drawn images of a similar function, which is now called the Koch snowflake. Another milestone came a decade later in 1915, when Wacław Sierpiński constructed his famous triangle then, one year later, his carpet. By 1918, two French mathematicians, Pierre Fatou and Gaston Julia, though working independently, arrived essentially simultaneously at results describing what is now seen as fractal behaviour associated with mapping complex numbers and iterative functions and leading to further ideas about attractors and repellors (i.e., points that attract or repel other points), which have become very important in the study of fractals.

Very shortly after that work was submitted, by March 1918, Felix Hausdorff expanded the definition of "dimension", significantly for the evolution of the definition of fractals, to allow for sets to have non-integer dimensions. The idea of self-similar curves was taken further by Paul Lévy, who, in his 1938 paper ''Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole'', described a new fractal curve, the Lévy C curve.

Different researchers have postulated that without the aid of modern computer graphics, early investigators were limited to what they could depict in manual drawings, so lacked the means to visualize the beauty and appreciate some of the implications of many of the patterns they had discovered (the Julia set, for instance, could only be visualized through a few iterations as very simple drawings). That changed, however, in the 1960s, when Benoit Mandelbrot started writing about self-similarity in papers such as ''How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension'', which built on earlier work by Lewis Fry Richardson.

In 1975 Mandelbrot solidified hundreds of years of thought and mathematical development in coining the word "fractal" and illustrated his mathematical definition with striking computer-constructed visualizations. These images, such as of his canonical Mandelbrot set, captured the popular imagination; many of them were based on recursion, leading to the popular meaning of the term "fractal".

In 1980, Loren Carpenter gave a presentation at the SIGGRAPH where he introduced his software for generating and rendering fractally generated landscapes.

Definition and characteristics

One often cited description that Mandelbrot published to describe geometric fractals is "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole"; this is generally helpful but limited. Authors disagree on the exact definition of ''fractal'', but most usually elaborate on the basic ideas of self-similarity and the unusual relationship fractals have with the space they are embedded in.

One point agreed on is that fractal patterns are characterized by fractal dimensions, but whereas these numbers quantify complexity (i.e., changing detail with changing scale), they neither uniquely describe nor specify details of how to construct particular fractal patterns. In 1975 when Mandelbrot coined the word "fractal", he did so to denote an object whose Hausdorff–Besicovitch dimension is greater than its topological dimension. However, this requirement is not met by space-filling curves such as the Hilbert curve.

Because of the trouble involved in finding one definition for fractals, some argue that fractals should not be strictly defined at all. According to Falconer, fractals should be only generally characterized by a gestalt of the following features;

* Self-similarity, which may include:
:* Exact self-similarity: identical at all scales, such as the Koch snowflake
:* Quasi self-similarity: approximates the same pattern at different scales; may contain small copies of the entire fractal in distorted and degenerate forms; e.g., the Mandelbrot set's satellites are approximations of the entire set, but not exact copies.
:* Statistical self-similarity: repeats a pattern stochastically so numerical or statistical measures are preserved across scales; e.g., randomly generated fractals like the well-known example of the coastline of Britain for which one would not expect to find a segment scaled and repeated as neatly as the repeated unit that defines fractals like the Koch snowflake.
:* Qualitative self-similarity: as in a time series
:* Multifractal scaling: characterized by more than one fractal dimension or scaling rule
* Fine or detailed structure at arbitrarily small scales. A consequence of this structure is fractals may have emergent properties (related to the next criterion in this list).
* Irregularity locally and globally that cannot easily be described in the language of traditional Euclidean geometry other than as the limit of a recursively defined sequence of stages. For images of fractal patterns, this has been expressed by phrases such as "smoothly piling up surfaces" and "swirls upon swirls";''see Common techniques for generating fractals''.

As a group, these criteria form guidelines for excluding certain cases, such as those that may be self-similar without having other typically fractal features. A straight line, for instance, is self-similar but not fractal because it lacks detail, and is easily described in Euclidean language without a need for recursion.

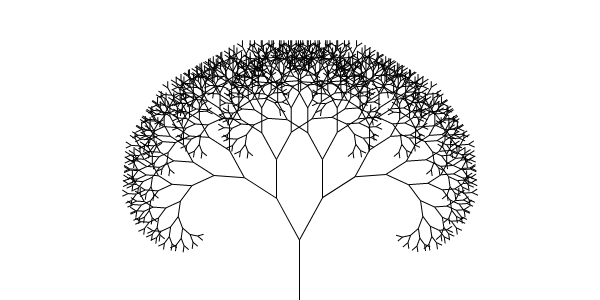
Common techniques for generating fractals

Images of fractals can be created by fractal generating programs. Because of the butterfly effect, a small change in a single variable can have an unpredictable outcome.

* ''Iterated function systems (IFS)'' – use fixed geometric replacement rules; may be stochastic or deterministic; e.g., Koch snowflake, Cantor set, Haferman carpet, Sierpinski carpet, Sierpinski gasket, Peano curve, Harter-Heighway dragon curve, T-square, Menger sponge
* ''Strange attractors'' – use iterations of a map or solutions of a system of initial-value differential or difference equations that exhibit chaos (e.g., see multifractal image, or the logistic map)
* ''L-systems'' – use string rewriting; may resemble branching patterns, such as in plants, biological cells (e.g., neurons and immune system cells), blood vessels, pulmonary structure, etc. or turtle graphics patterns such as space-filling curves and tilings
* ''Escape-time fractals'' – use a formula or recurrence relation at each point in a space (such as the complex plane); usually quasi-self-similar; also known as "orbit" fractals; e.g., the Mandelbrot set, Julia set, Burning Ship fractal, Nova fractal and Lyapunov fractal. The 2d vector fields that are generated by one or two iterations of escape-time formulae also give rise to a fractal form when points (or pixel data) are passed through this field repeatedly.
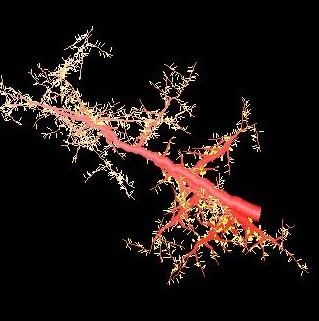
* ''Random fractals'' – use stochastic rules; e.g., Lévy flight, percolation clusters, self avoiding walks, fractal landscapes, trajectories of Brownian motion and the Brownian tree (i.e., dendritic fractals generated by modeling diffusion-limited aggregation or reaction-limited aggregation clusters).

*''Finite subdivision rules'' – use a recursive topological algorithm for refining tilingsJ. W. Cannon, W. J. Floyd, W. R. Parry. ''Finite subdivision rules''. Conformal Geometry and Dynamics, vol. 5 (2001), pp. 153–196. and they are similar to the process of cell division.J. W. Cannon, W. Floyd and W. Parry
''Crystal growth, biological cell growth and geometry''.
Pattern Formation in Biology, Vision and Dynamics, pp. 65–82. World Scientific, 2000. , . The iterative processes used in creating the Cantor set and the Sierpinski carpet are examples of finite subdivision rules, as is barycentric subdivision.

Applications

Simulated fractals

Fractal patterns have been modeled extensively, albeit within a range of scales rather than infinitely, owing to the practical limits of physical time and space. Models may simulate theoretical fractals or natural phenomena with fractal features. The outputs of the modelling process may be highly artistic renderings, outputs for investigation, or benchmarks for fractal analysis. Some specific applications of fractals to technology are listed elsewhere. Images and other outputs of modelling are normally referred to as being "fractals" even if they do not have strictly fractal characteristics, such as when it is possible to zoom into a region of the fractal image that does not exhibit any fractal properties. Also, these may include calculation or display artifacts which are not characteristics of true fractals.

Modeled fractals may be sounds, digital images, electrochemical patterns, circadian rhythms, etc.
Fractal patterns have been reconstructed in physical 3-dimensional space and virtually, often called "in silico" modeling. Models of fractals are generally created using fractal-generating software that implements techniques such as those outlined above. As one illustration, trees, ferns, cells of the nervous system, blood and lung vasculature, and other branching patterns in nature can be modeled on a computer by using recursive algorithms and L-systems techniques.

The recursive nature of some patterns is obvious in certain examples—a branch from a tree or a frond from a fern is a miniature replica of the whole: not identical, but similar in nature. Similarly, random fractals have been used to describe/create many highly irregular real-world objects. A limitation of modeling fractals is that resemblance of a fractal model to a natural phenomenon does not prove that the phenomenon being modeled is formed by a process similar to the modeling algorithms.

Natural phenomena with fractal features

Approximate fractals found in nature display self-similarity over extended, but finite, scale ranges. The connection between fractals and leaves, for instance, is currently being used to determine how much carbon is contained in trees. Phenomena known to have fractal features include:

* Actin cytoskeleton
* Algae
* Animal coloration patterns
* Blood vessels and pulmonary vessels
* Brownian motion (generated by a one-dimensional Wiener process).
* Clouds and rainfall areas
* Coastlines
* Craters
* Crystals
* DNA
* Dust grains
* Earthquakes
* Fault lines
* Geometrical optics
* Heart rates
* Heart sounds
*Lake shorelines and areas
* Lightning bolts
* Mountain goat horns
* Polymers
* Percolation
* Mountain ranges
* Ocean waves
* Pineapple
* Proteins
* Psychedelic Experience
*Purkinje cells
* Rings of Saturn
* River networks
* Romanesco broccoli
* Snowflakes
* Soil pores
*Surfaces in turbulent flows
* Trees

File:Frost patterns 2.jpg, Frost crystals occurring naturally on cold glass form fractal patterns
File:Optical Billiard Spheres dsweet.jpeg, Fractal basin boundary in a geometrical optical system
File:Glue1 800x600.jpg, A fractal is formed when pulling apart two glue-covered acrylic sheets
File:Square1.jpg, High-voltage breakdown within a block of acrylic glass creates a fractal Lichtenberg figure
File:Romanesco broccoli (Brassica oleracea).jpg, Romanesco broccoli, showing self-similar form approximating a natural fractal
File:Fractal defrosting patterns on Mars.jpg, Fractal defrosting patterns, polar Mars. The patterns are formed by sublimation of frozen CO₂. Width of image is about a kilometer.
File:Brefeldia maxima plasmodium on wood.jpg, Slime mold ''Brefeldia maxima'' growing fractally on wood

Fractals in cell biology

Fractals often appear in the realm of living organisms where they arise through branching processes and other complex pattern formation. Ian Wong and co-workers have shown that migrating cells can form fractals by clustering and branching. Nerve cells function through processes at the cell surface, with phenomena that are enhanced by largely increasing the surface to volume ratio. As a consequence nerve cells often are found to form into fractal patterns. These processes are crucial in cell physiology and different pathologies.

Multiple subcellular structures also are found to assemble into fractals. Diego Krapf has shown that through branching processes the actin filaments in human cells assemble into fractal patterns. Similarly Matthias Weiss showed that the endoplasmic reticulum displays fractal features. The current understanding is that fractals are ubiquitous in cell biology, from proteins, to organelles, to whole cells.

In creative works

Since 1999 numerous scientific groups have performed fractal analysis on over 50 paintings created by Jackson Pollock by pouring paint directly onto horizontal canvasses.

Recently, fractal analysis has been used to achieve a 93% success rate in distinguishing real from imitation Pollocks. Cognitive neuroscientists have shown that Pollock's fractals induce the same stress-reduction in observers as computer-generated fractals and Nature's fractals.

Decalcomania, a technique used by artists such as Max Ernst, can produce fractal-like patterns. It involves pressing paint between two surfaces and pulling them apart.

Cyberneticist Ron Eglash has suggested that fractal geometry and mathematics are prevalent in African art, games, divination, trade, and architecture. Circular houses appear in circles of circles, rectangular houses in rectangles of rectangles, and so on. Such scaling patterns can also be found in African textiles, sculpture, and even cornrow hairstyles. Hokky Situngkir also suggested the similar properties in Indonesian traditional art, batik, and ornaments found in traditional houses.

Ethnomathematician Ron Eglash has discussed the planned layout of Benin city using fractals as the basis, not only in the city itself and the villages but even in the rooms of houses. He commented that "When Europeans first came to Africa, they considered the architecture very disorganised and thus primitive. It never occurred to them that the Africans might have been using a form of mathematics that they hadn’t even discovered yet."

In a 1996 interview with Michael Silverblatt, David Foster Wallace admitted that the structure of the first draft of ''Infinite Jest'' he gave to his editor Michael Pietsch was inspired by fractals, specifically the Sierpinski triangle (a.k.a. Sierpinski gasket), but that the edited novel is "more like a lopsided Sierpinsky Gasket".

Some works by the Dutch artist M. C. Escher, such as Circle Limit III, contain shapes repeated to infinity that become smaller and smaller as they get near to the edges, in a pattern that would always look the same if zoomed in.

File:Animated fractal mountain.gif, A fractal that models the surface of a mountain (animation)
File:FRACTAL-3d-FLOWER.jpg, 3D recursive image
File:Fractal-BUTTERFLY.jpg, Recursive fractal butterfly image
File:Apophysis-100303-104.jpg, A fractal flame

Physiological responses

Humans appear to be especially well-adapted to processing fractal patterns with D values between 1.3 and 1.5. When humans view fractal patterns with D values between 1.3 and 1.5, this tends to reduce physiological stress.

Applications in technology

* Fractal antennas
*Fractal transistor
* Fractal heat exchangers
* Digital imaging
* Architecture
* Urban growth
* Classification of histopathology slides
* Fractal landscape or Coastline complexity
* Detecting 'life as we don't know it' by fractal analysis
* Enzymes ( Michaelis-Menten kinetics)
* Generation of new music
* Signal and image compression
* Creation of digital photographic enlargements
* Fractal in soil mechanics
* Computer and video game design
* Computer Graphics
* Organic environments
* Procedural generation
* Fractography and fracture mechanics
* Small angle scattering theory of fractally rough systems
* T-shirts and other fashion
* Generation of patterns for camouflage, such as MARPAT
* Digital sundial
* Technical analysis of price series
* Fractals in networks
* Medicine
* Neuroscience
* Diagnostic Imaging
* Pathology
* Geology
*Geography
* Archaeology
* Soil mechanics
* Seismology
* Search and rescue
* Technical analysis
* Morton order space filling curves for GPU cache coherency in texture mapping, rasterisation and indexing of turbulence data.

See also

*Banach fixed point theorem
*Bifurcation theory
*Box counting
*Cymatics
*Determinism
*Diamond-square algorithm
*Droste effect
*Feigenbaum function
*Form constant
*Fractal cosmology
*Fractal derivative
*Fractalgrid
*Fractal string
*Fracton
* Graftal
*Greeble
*Infinite regress
*Lacunarity
*List of fractals by Hausdorff dimension
*Mandelbulb
*Mandelbox
* Macrocosm and microcosm
*Matryoshka doll
*Menger Sponge
*Multifractal system
*Newton fractal
*Percolation
*Power law
* Publications in fractal geometry
*Random walk
*Self-reference
*Self-similarity
*Systems theory
*Strange loop
*Turbulence
*Wiener process

Notes

References

Further reading

* Barnsley, Michael F.; and Rising, Hawley; ''Fractals Everywhere''. Boston: Academic Press Professional, 1993.
* Duarte, German A.; ''Fractal Narrative. About the Relationship Between Geometries and Technology and Its Impact on Narrative Spaces''. Bielefeld: Transcript, 2014.
* Falconer, Kenneth; ''Techniques in Fractal Geometry''. John Wiley and Sons, 1997.
* Jürgens, Hartmut; Peitgen, Heinz-Otto; and Saupe, Dietmar; ''Chaos and Fractals: New Frontiers of Science''. New York: Springer-Verlag, 1992.
* Mandelbrot, Benoit B.; ''The Fractal Geometry of Nature''. New York: W. H. Freeman and Co., 1982.
* Peitgen, Heinz-Otto; and Saupe, Dietmar; eds.; ''The Science of Fractal Images''. New York: Springer-Verlag, 1988.
* Pickover, Clifford A.; ed.; ''Chaos and Fractals: A Computer Graphical Journey – A 10 Year Compilation of Advanced Research''. Elsevier, 1998.
* Jones, Jesse; ''Fractals for the Macintosh'', Waite Group Press, Corte Madera, CA, 1993. .
* Lauwerier, Hans; ''Fractals: Endlessly Repeated Geometrical Figures'', Translated by Sophia Gill-Hoffstadt, Princeton University Press, Princeton NJ, 1991. , cloth. paperback. "This book has been written for a wide audience..." Includes sample BASIC programs in an appendix.
*
* Wahl, Bernt; Van Roy, Peter; Larsen, Michael; and Kampman, Eric
''Exploring Fractals on the Macintosh''
Addison Wesley, 1995.
* Lesmoir-Gordon, Nigel; ''The Colours of Infinity: The Beauty, The Power and the Sense of Fractals''. 2004. (The book comes with a related DVD of the Arthur C. Clarke documentary introduction to the fractal concept and the Mandelbrot set.)
* Liu, Huajie; ''Fractal Art'', Changsha: Hunan Science and Technology Press, 1997, .
* Gouyet, Jean-François; ''Physics and Fractal Structures'' (Foreword by B. Mandelbrot); Masson, 1996. , and New York: Springer-Verlag, 1996. . Out-of-print. Available in PDF version at.
*

External links

*

Hunting the Hidden Dimension
PBS ''NOVA'', first aired August 24, 2011

Benoit Mandelbrot: Fractals and the Art of Roughness
, TED, February 2010

Technical Library on Fractals for controlling fluid

Equations of self-similar fractal measure based on the fractional-order calculus
��2007）

{{Authority control

Mathematical structures
Topology
Computational fields of study