
Concrete is a
composite material
A composite or composite material (also composition material) is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a ...
composed of
aggregate bound together with a fluid
cement that
cures to a
solid
Solid is a state of matter where molecules are closely packed and can not slide past each other. Solids resist compression, expansion, or external forces that would alter its shape, with the degree to which they are resisted dependent upon the ...
over time. It is the second-most-used substance (after
water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
), the most–widely used building material, and the most-manufactured material in the world.
When aggregate is mixed with dry
Portland cement and
water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
, the mixture forms a fluid
slurry that can be poured and molded into shape. The cement reacts with the water through a process called hydration, which hardens it after several hours to form a solid matrix that binds the materials together into a durable stone-like material with various uses. This time allows concrete to not only be cast in forms, but also to have a variety of tooled processes performed. The hydration process is
exothermic, which means that
ambient temperature plays a significant role in how long it takes concrete to set. Often, additives (such as
pozzolans or
superplasticizers) are included in the mixture to improve the physical properties of the wet mix, delay or accelerate the curing time, or otherwise modify the finished material. Most structural concrete is poured with reinforcing materials (such as steel
rebar) embedded to provide
tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
, yielding
reinforced concrete.
Before the invention of Portland cement in the early 1800s,
lime-based cement binders, such as lime putty, were often used. The overwhelming majority of concretes are produced using Portland cement, but sometimes with other
hydraulic cements, such as
calcium aluminate cement. Many other non-cementitious
types of concrete exist with other methods of binding aggregate together, including
asphalt concrete with a
bitumen
Bitumen ( , ) is an immensely viscosity, viscous constituent of petroleum. Depending on its exact composition, it can be a sticky, black liquid or an apparently solid mass that behaves as a liquid over very large time scales. In American Engl ...
binder, which is frequently used for
road surfaces, and
polymer concretes that use polymers as a binder.
Concrete is distinct from
mortar. Whereas concrete is itself a building material, and contains both coarse (large) and fine (small) aggregate particles, mortar contains only fine aggregates and is mainly used as a bonding agent to hold
brick
A brick is a type of construction material used to build walls, pavements and other elements in masonry construction. Properly, the term ''brick'' denotes a unit primarily composed of clay. But is now also used informally to denote building un ...
s,
tiles and other masonry units together.
Grout is another material associated with concrete and cement. It also does not contain coarse aggregates and is usually either pourable or
thixotropic, and is used to fill gaps between masonry components or coarse aggregate which has already been put in place. Some methods of concrete manufacture and repair involve pumping grout into the gaps to make up a solid mass ''in situ''.
Etymology
The word concrete comes from the
Latin
Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally spoken by the Latins (Italic tribe), Latins in Latium (now known as Lazio), the lower Tiber area aroun ...
word "" (meaning compact or condensed), the perfect passive participle of "", from "-" (together) and "" (to grow).
History
Ancient times
Concrete floors were found in the royal palace of
Tiryns, Greece, which dates roughly to 1400 to 1200 BC. Lime mortars were used in Greece, such as in Crete and Cyprus, in 800 BC. The
Assyria
Assyria (Neo-Assyrian cuneiform: , ''māt Aššur'') was a major ancient Mesopotamian civilization that existed as a city-state from the 21st century BC to the 14th century BC and eventually expanded into an empire from the 14th century BC t ...
n Jerwan Aqueduct (688 BC) made use of
waterproof concrete. Concrete was used for construction in many ancient structures.
Mayan concrete at the ruins of
Uxmal (AD 850–925) is referenced in ''Incidents of Travel in the Yucatán'' by
John L. Stephens. "The roof is flat and had been covered with cement". "The floors were cement, in some places hard, but, by long exposure, broken, and now crumbling under the feet." "But throughout the wall was solid, and consisting of large stones imbedded in mortar, almost as hard as rock."
Small-scale production of concrete-like materials was pioneered by the
Nabatean traders who occupied and controlled a series of oases and developed a small empire in the regions of southern Syria and northern Jordan from the 4th century BC. They discovered the advantages of
hydraulic lime
Hydraulic lime (HL) is a general term for a variety of lime different from calcium oxide (quicklime), that sets by hydration and consists of calcium silicate and calcium aluminate, compounds that can harden in contact with water. This contras ...
, with some self-cementing properties, by 700 BC. They built
kiln
A kiln is a thermally insulated chamber, a type of oven, that produces temperatures sufficient to complete some process, such as hardening, drying, or Chemical Changes, chemical changes. Kilns have been used for millennia to turn objects m ...
s to supply mortar for the construction of
rubble masonry
Rubble masonry or rubble stone is rough, uneven building stone not laid in regular courses. It may fill the core of a wall which is faced with unit masonry such as brick or ashlar. Some medieval cathedral walls have outer shells of ashlar wi ...
houses, concrete floors, and underground waterproof
cisterns. They kept the cisterns secret as these enabled the Nabataeans to thrive in the desert.
Some of these structures survive to this day.
In the
Ancient Egypt
Ancient Egypt () was a cradle of civilization concentrated along the lower reaches of the Nile River in Northeast Africa. It emerged from prehistoric Egypt around 3150BC (according to conventional Egyptian chronology), when Upper and Lower E ...
ian and later
Roman eras, builders discovered that adding
volcanic ash
Volcanic ash consists of fragments of rock, mineral crystals, and volcanic glass, produced during volcanic eruptions and measuring less than 2 mm (0.079 inches) in diameter. The term volcanic ash is also often loosely used to r ...
to
lime allowed the mix to set underwater. They discovered the
pozzolanic reaction.
Classical era

The Romans used concrete extensively from 300 BC to AD 476.
During the Roman Empire,
Roman concrete (or ''
opus caementicium'') was made from
quicklime,
pozzolana
Pozzolana or pozzuolana ( , ), also known as pozzolanic ash (), is a natural siliceous or siliceous- aluminous material which reacts with calcium hydroxide in the presence of water at room temperature (cf. pozzolanic reaction). In this reaction ...
and an aggregate of
pumice. Its widespread use in many
Roman structures, a key event in the
history of architecture
The history of architecture traces the changes in architecture through various traditions, regions, overarching stylistic trends, and dates. The beginnings of all these traditions is thought to be humans satisfying the very basic need of shelt ...
termed the
Roman architectural revolution, freed
Roman construction from the restrictions of stone and brick materials. It enabled revolutionary new designs in terms of both structural complexity and dimension. The
Colosseum in Rome was built largely of concrete, and the
Pantheon has the world's largest unreinforced concrete dome.
Concrete, as the Romans knew it, was a new and revolutionary material. Laid in the shape of arches, vaults and domes, it quickly hardened into a rigid mass, free from many of the internal thrusts and strains that troubled the builders of similar structures in stone or brick.
Modern tests show that ''opus caementicium'' had a similar compressive strength to modern Portland-cement concrete (c. ). However, due to the absence of reinforcement, its
tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
was far lower than modern
reinforced concrete, and its mode of application also differed:
Modern structural concrete differs from Roman concrete in two important details. First, its mix consistency is fluid and homogeneous, allowing it to be poured into forms rather than requiring hand-layering together with the placement of aggregate, which, in Roman practice, often consisted of rubble. Second, integral reinforcing steel gives modern concrete assemblies great strength in tension, whereas Roman concrete could depend only upon the strength of the concrete bonding to resist tension.
The long-term durability of Roman concrete structures was found to be due to the presence of
pyroclastic (volcanic) rock and ash in the concrete mix. The crystallization of
strätlingite (a complex calcium aluminosilicate hydrate) during the formation of the concrete and its merging with similar calcium–aluminium-silicate–hydrate structures helped give the Roman concrete a greater degree of fracture resistance compared to modern concrete. In addition, Roman concrete is significantly more resistant to erosion by seawater than modern concrete; the aforementioned pyroclastic materials react with seawater to form Al-
tobermorite crystals over time. The use of hot mixing in preparation of concrete, leading to the formation of lime clasts in the final product, has been proposed to give the Roman concrete a
self-healing ability.
The widespread use of concrete in many Roman structures ensured that many survive to the present day. The
Baths of Caracalla
The Baths of Caracalla () in Rome, Italy, were the city's second largest Ancient Rome, Roman public baths, or ''thermae'', after the Baths of Diocletian. The baths were likely built between AD 212 (or 211) and 216/217, during the reigns of empero ...
in Rome are just one example. Many
Roman aqueducts and bridges, such as the magnificent
Pont du Gard in southern France, have masonry cladding on a concrete core, as does the dome of the
Pantheon.
Middle Ages
After the Roman Empire, the use of burned lime and pozzolana was greatly reduced. Low kiln temperatures in the burning of lime, lack of pozzolana, and poor mixing all contributed to a decline in the quality of concrete and mortar. From the 11th century, the increased use of stone in church and
castle
A castle is a type of fortification, fortified structure built during the Middle Ages predominantly by the nobility or royalty and by Military order (monastic society), military orders. Scholars usually consider a ''castle'' to be the private ...
construction led to an increased demand for mortar. Quality began to improve in the 12th century through better grinding and sieving. Medieval lime mortars and concretes were non-hydraulic and were used for binding masonry, "hearting" (binding
rubble masonry
Rubble masonry or rubble stone is rough, uneven building stone not laid in regular courses. It may fill the core of a wall which is faced with unit masonry such as brick or ashlar. Some medieval cathedral walls have outer shells of ashlar wi ...
cores) and foundations.
Bartholomaeus Anglicus in his ''De proprietatibus rerum'' (1240) describes the making of mortar. In an English translation from 1397, it reads "lyme ... is a stone brent; by medlynge thereof with sonde and water sement is made". From the 14th century, the quality of mortar was again excellent, but only from the 17th century was pozzolana commonly added.
The ''
Canal du Midi'' was built using concrete in 1670.
Industrial era
Perhaps the greatest step forward in the modern use of concrete was
Smeaton's Tower
Smeaton's Tower is a redundant lighthouse, now a memorial to civil engineer John Smeaton, designer of the third and most notable Eddystone Lighthouse#Smeaton.27s lighthouse, Eddystone Lighthouse. A major step forward in lighthouse design, Smeat ...
, built by British engineer
John Smeaton
John Smeaton (8 June 1724 – 28 October 1792) was an English civil engineer responsible for the design of bridges, canals, harbours and lighthouses. He was also a capable mechanical engineer and an eminent scholar, who introduced various ...
in
Devon
Devon ( ; historically also known as Devonshire , ) is a ceremonial county in South West England. It is bordered by the Bristol Channel to the north, Somerset and Dorset to the east, the English Channel to the south, and Cornwall to the west ...
, England, between 1756 and 1759. This third
Eddystone Lighthouse pioneered the use of
hydraulic lime
Hydraulic lime (HL) is a general term for a variety of lime different from calcium oxide (quicklime), that sets by hydration and consists of calcium silicate and calcium aluminate, compounds that can harden in contact with water. This contras ...
in concrete, using pebbles and powdered brick as aggregate.
A method for producing
Portland cement was developed in England and patented by
Joseph Aspdin in 1824. Aspdin chose the name for its similarity to
Portland stone, which was quarried on the
Isle of Portland in
Dorset
Dorset ( ; Archaism, archaically: Dorsetshire , ) is a Ceremonial counties of England, ceremonial county in South West England. It is bordered by Somerset to the north-west, Wiltshire to the north and the north-east, Hampshire to the east, t ...
, England. His son
William
William is a masculine given name of Germanic languages, Germanic origin. It became popular in England after the Norman Conquest, Norman conquest in 1066,All Things William"Meaning & Origin of the Name"/ref> and remained so throughout the Middle ...
continued developments into the 1840s, earning him recognition for the development of "modern" Portland cement.
Reinforced concrete was invented in 1849 by
Joseph Monier. and the first reinforced concrete house was built by François Coignet
in 1853.
The first concrete reinforced bridge was designed and built by
Joseph Monier in 1875.
Prestressed concrete and
post-tensioned concrete were pioneered by
Eugène Freyssinet, a French
structural and
civil engineer. Concrete components or structures are compressed by tendon cables during, or after, their fabrication in order to strengthen them against
tensile forces developing when put in service. Freyssinet
patent
A patent is a type of intellectual property that gives its owner the legal right to exclude others from making, using, or selling an invention for a limited period of time in exchange for publishing an sufficiency of disclosure, enabling discl ...
ed the technique on 2 October 1928.
Composition
Concrete is an artificial
composite material
A composite or composite material (also composition material) is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a ...
, comprising a matrix of cementitious binder (typically
Portland cement paste or
asphalt) and a dispersed phase or "filler" of
aggregate (typically a rocky material, loose stones, and sand). The binder "glues" the filler together to form a synthetic
conglomerate.
Many
types of concrete are available, determined by the formulations of binders and the types of aggregate used to suit the application of the engineered material. These variables determine strength and density, as well as chemical and thermal resistance of the finished product.
 Construction aggregate
Construction aggregates consist of large chunks of material in a concrete mix, generally a coarse
gravel or crushed rocks such as
limestone
Limestone is a type of carbonate rock, carbonate sedimentary rock which is the main source of the material Lime (material), lime. It is composed mostly of the minerals calcite and aragonite, which are different Polymorphism (materials science) ...
, or
granite
Granite ( ) is a coarse-grained (phanerite, phaneritic) intrusive rock, intrusive igneous rock composed mostly of quartz, alkali feldspar, and plagioclase. It forms from magma with a high content of silica and alkali metal oxides that slowly coo ...
, along with finer materials such as
sand
Sand is a granular material composed of finely divided mineral particles. Sand has various compositions but is usually defined by its grain size. Sand grains are smaller than gravel and coarser than silt. Sand can also refer to a textural ...
.
Cement paste, most commonly made of
Portland cement, is the most prevalent kind of concrete binder. For cementitious binders,
water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
is mixed with the dry cement powder and aggregate, which produces a semi-liquid slurry (paste) that can be shaped, typically by pouring it into a form. The concrete solidifies and hardens through a
chemical process
In a scientific sense, a chemical process is a method or means of somehow changing one or more chemicals or chemical compounds. Such a chemical process can occur by itself or be caused by an outside force, and involves a chemical reaction of som ...
called
hydration. The water reacts with the cement, which bonds the other components together, creating a robust, stone-like material. Other cementitious materials, such as
fly ash
Coal combustion products (CCPs), also called coal combustion wastes (CCWs) or coal combustion residuals (CCRs), are byproducts of burning coal. They are categorized in four groups, each based on physical and chemical forms derived from coal combust ...
and
slag cement, are sometimes added—either pre-blended with the cement or directly as a concrete component—and become a part of the binder for the aggregate.
Fly ash and slag can enhance some properties of concrete such as fresh properties and durability.
[ Alternatively, other materials can also be used as a concrete binder: the most prevalent substitute is asphalt, which is used as the binder in asphalt concrete.
Admixtures are added to modify the cure rate or properties of the material. Mineral admixtures use recycled materials as concrete ingredients. Conspicuous materials include ]fly ash
Coal combustion products (CCPs), also called coal combustion wastes (CCWs) or coal combustion residuals (CCRs), are byproducts of burning coal. They are categorized in four groups, each based on physical and chemical forms derived from coal combust ...
, a by-product of coal-fired power plants; ground granulated blast furnace slag, a by-product of steelmaking; and silica fume, a by-product of industrial electric arc furnaces.
Structures employing Portland cement concrete usually include steel reinforcement because this type of concrete can be formulated with high compressive strength, but always has lower tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
. Therefore, it is usually reinforced with materials that are strong in tension, typically steel
Steel is an alloy of iron and carbon that demonstrates improved mechanical properties compared to the pure form of iron. Due to steel's high Young's modulus, elastic modulus, Yield (engineering), yield strength, Fracture, fracture strength a ...
rebar.
The '' mix design'' depends on the type of structure being built, how the concrete is mixed and delivered, and how it is placed to form the structure.
Cement
 Portland cement is the most common type of cement in general usage. It is a basic ingredient of concrete, mortar, and many plasters. It consists of a mixture of calcium silicates ( alite, belite), aluminates and
Portland cement is the most common type of cement in general usage. It is a basic ingredient of concrete, mortar, and many plasters. It consists of a mixture of calcium silicates ( alite, belite), aluminates and ferrites Ferrite may refer to:
* Ferrite (iron), one of the allotropes of iron that is stable at room temperature and pressure, α-Fe
* Ferrite (magnet), a ferromagnetic ceramic material
See also
*
* Ferrite bead, a component placed on the end of a data c ...
—compounds, which will react with water. Portland cement and similar materials are made by heating limestone
Limestone is a type of carbonate rock, carbonate sedimentary rock which is the main source of the material Lime (material), lime. It is composed mostly of the minerals calcite and aragonite, which are different Polymorphism (materials science) ...
(a source of calcium) with clay or shale (a source of silicon, aluminium and iron) and grinding this product (called '' clinker'') with a source of sulfate (most commonly gypsum).
Cement kilns are extremely large, complex, and inherently dusty industrial installations. Of the various ingredients used to produce a given quantity of concrete, the cement is the most energetically expensive. Even complex and efficient kilns require 3.3 to 3.6 gigajoules of energy to produce a ton of clinker and then grind it into cement. Many kilns can be fueled with difficult-to-dispose-of wastes, the most common being used tires. The extremely high temperatures and long periods of time at those temperatures allows cement kilns to efficiently and completely burn even difficult-to-use fuels. The five major compounds of calcium silicates and aluminates comprising Portland cement range from 5 to 50% in weight.
Curing
Combining water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
with a cementitious material forms a cement paste by the process of hydration. The cement paste glues the aggregate together, fills voids within it, and makes it flow more freely.
As stated by Abrams' law, a lower water-to-cement ratio yields a stronger, more durable concrete, whereas more water gives a freer-flowing concrete with a higher slump. The hydration of cement involves many concurrent reactions. The process involves polymerization
In polymer chemistry, polymerization (American English), or polymerisation (British English), is a process of reacting monomer molecules together in a chemical reaction to form polymer chains or three-dimensional networks. There are many fo ...
, the interlinking of the silicates and aluminate components as well as their bonding to sand and gravel particles to form a solid mass.
Aggregates
 Fine and coarse aggregates make up the bulk of a concrete mixture.
Fine and coarse aggregates make up the bulk of a concrete mixture. Sand
Sand is a granular material composed of finely divided mineral particles. Sand has various compositions but is usually defined by its grain size. Sand grains are smaller than gravel and coarser than silt. Sand can also refer to a textural ...
, natural gravel, and crushed stone are used mainly for this purpose. Recycled aggregates (from construction, demolition, and excavation waste) are increasingly used as partial replacements for natural aggregates, while a number of manufactured aggregates, including air-cooled blast furnace slag and bottom ash
Bottom ash is part of the non- combustible residue of combustion in a power plant, boiler, furnace, or incinerator. In an industrial context, it has traditionally referred to coal combustion and comprises traces of combustibles embedded in for ...
are also permitted.
The size distribution of the aggregate determines how much binder is required. Aggregate with a very even size distribution has the biggest gaps whereas adding aggregate with smaller particles tends to fill these gaps. The binder must fill the gaps between the aggregate as well as paste the surfaces of the aggregate together, and is typically the most expensive component. Thus, variation in sizes of the aggregate reduces the cost of concrete. The aggregate is nearly always stronger than the binder, so its use does not negatively affect the strength of the concrete.
Redistribution of aggregates after compaction often creates non-homogeneity due to the influence of vibration. This can lead to strength gradients.
Admixtures
Admixtures are materials in the form of powder or fluids that are added to the concrete to give it certain characteristics not obtainable with plain concrete mixes. Admixtures are defined as additions "made as the concrete mix is being prepared".Pigment
A pigment is a powder used to add or alter color or change visual appearance. Pigments are completely or nearly solubility, insoluble and reactivity (chemistry), chemically unreactive in water or another medium; in contrast, dyes are colored sub ...
s can be used to change the color of concrete, for aesthetics.
* Plasticizers increase the workability of plastic, or "fresh", concrete, allowing it to be placed more easily, with less consolidating effort. A typical plasticizer is lignosulfonate. Plasticizers can be used to reduce the water content of a concrete while maintaining workability and are sometimes called water-reducers due to this use. Such treatment improves its strength and durability characteristics.
* Superplasticizers (also called high-range water-reducers) are a class of plasticizers that have fewer deleterious effects and can be used to increase workability more than is practical with traditional plasticizers. Superplasticizers are used to increase compressive strength. It increases the workability of the concrete and lowers the need for water content by 15–30%.
* Pumping aids improve pumpability, thicken the paste and reduce separation and bleeding.
* Retarders slow the hydration of concrete and are used in large or difficult pours where partial setting is undesirable before completion of the pour. Typical retarders include sugar
Sugar is the generic name for sweet-tasting, soluble carbohydrates, many of which are used in food. Simple sugars, also called monosaccharides, include glucose
Glucose is a sugar with the Chemical formula#Molecular formula, molecul ...
, sodium gluconate, citric acid, and tartaric acid.
Mineral admixtures and blended cements
Inorganic materials that have pozzolanic or latent hydraulic properties, these very fine-grained materials are added to the concrete mix to improve the properties of concrete (mineral admixtures),limestone
Limestone is a type of carbonate rock, carbonate sedimentary rock which is the main source of the material Lime (material), lime. It is composed mostly of the minerals calcite and aragonite, which are different Polymorphism (materials science) ...
, fly ash
Coal combustion products (CCPs), also called coal combustion wastes (CCWs) or coal combustion residuals (CCRs), are byproducts of burning coal. They are categorized in four groups, each based on physical and chemical forms derived from coal combust ...
, blast furnace slag, and other useful materials with pozzolanic properties into the mix, are being tested and used. These developments are ever growing in relevance to minimize the impacts caused by cement use, notorious for being one of the largest producers (at about 5 to 10%) of global greenhouse gas emissions
Greenhouse gas (GHG) emissions from human activities intensify the greenhouse effect. This contributes to climate change. Carbon dioxide (), from burning fossil fuels such as coal, petroleum, oil, and natural gas, is the main cause of climate chan ...
.landfill
A landfill is a site for the disposal of waste materials. It is the oldest and most common form of waste disposal, although the systematic burial of waste with daily, intermediate and final covers only began in the 1940s. In the past, waste was ...
practices.
* Fly ash
Coal combustion products (CCPs), also called coal combustion wastes (CCWs) or coal combustion residuals (CCRs), are byproducts of burning coal. They are categorized in four groups, each based on physical and chemical forms derived from coal combust ...
: A by-product of coal-fired electric generating plants, it is used to partially replace Portland cement (by up to 60% by mass). The properties of fly ash depend on the type of coal burnt. In general, siliceous fly ash is pozzolanic, while calcareous fly ash has latent hydraulic properties.
* Ground granulated blast furnace slag (GGBFS or GGBS): A by-product of steel production is used to partially replace Portland cement (by up to 80% by mass). It has latent hydraulic properties.
* Silica fume: A by-product of the production of silicon and ferrosilicon
Ferrosilicon is an ferroalloy, alloy of iron and silicon. It has a typical silicon content of 15–90% by weight and a high proportion of iron silicides.
Production and reactions
Ferrosilicon is produced by reduction of silica or sand with coke ...
alloy
An alloy is a mixture of chemical elements of which in most cases at least one is a metal, metallic element, although it is also sometimes used for mixtures of elements; herein only metallic alloys are described. Metallic alloys often have prop ...
s. Silica fume is similar to fly ash, but has a particle size 100 times smaller. This results in a higher surface-to-volume ratio and a much faster pozzolanic reaction. Silica fume is used to increase strength and durability of concrete, but generally requires the use of superplasticizers for workability.
* High reactivity metakaolin (HRM): Metakaolin produces concrete with strength and durability similar to concrete made with silica fume. While silica fume is usually dark gray or black in color, high-reactivity metakaolin is usually bright white in color, making it the preferred choice for architectural concrete where appearance is important.
* Carbon nanofibers can be added to concrete to enhance compressive strength and gain a higher Young's modulus
Young's modulus (or the Young modulus) is a mechanical property of solid materials that measures the tensile or compressive stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Youn ...
, and also to improve the electrical properties required for strain monitoring, damage evaluation and self-health monitoring of concrete. Carbon fiber has many advantages in terms of mechanical and electrical properties (e.g., higher strength) and self-monitoring behavior due to the high tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
and high electrical conductivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity in ...
.
* Carbon products have been added to make concrete electrically conductive, for deicing purposes.
* New research from Japan's University of Kitakyushu shows that a washed and dried recycled mix of used diapers can be an environmental solution to producing less landfill and using less sand in concrete production. A model home was built in Indonesia to test the strength and durability of the new diaper-cement composite.
Production
Concrete production is the process of mixing together the various ingredients—water, aggregate, cement, and any additives—to produce concrete. Concrete production is time-sensitive. Once the ingredients are mixed, workers must put the concrete in place before it hardens. In modern usage, most concrete production takes place in a large type of industrial facility called a concrete plant, or often a batch plant. The usual method of placement is casting in formwork, which holds the mix in shape until it has set enough to hold its shape unaided.
Concrete plants come in two main types, ready-mix plants and central mix plants. A ready-mix plant blends all of the solid ingredients, while a central mix does the same but adds water. A central-mix plant offers more precise control of the concrete quality. Central mix plants must be close to the work site where the concrete will be used, since hydration begins at the plant.
A concrete plant consists of large hoppers for storage of various ingredients like cement, storage for bulk ingredients like aggregate and water, mechanisms for the addition of various additives and amendments, machinery to accurately weigh, move, and mix some or all of those ingredients, and facilities to dispense the mixed concrete, often to a concrete mixer truck.
Modern concrete is usually prepared as a viscous fluid, so that it may be poured into forms. The forms are containers that define the desired shape. Concrete formwork can be prepared in several ways, such as slip forming and steel plate construction. Alternatively, concrete can be mixed into dryer, non-fluid forms and used in factory settings to manufacture precast concrete
Precast concrete is a construction product produced by casting concrete in a reusable molding (process), mold or "form" which is then cured in a controlled environment, transported to the construction site and maneuvered into place; examples i ...
products.
Interruption in pouring the concrete can cause the initially placed material to begin to set before the next batch is added on top. This creates a horizontal plane of weakness called a ''cold joint'' between the two batches. Once the mix is where it should be, the curing process must be controlled to ensure that the concrete attains the desired attributes. During concrete preparation, various technical details may affect the quality and nature of the product.
Design mix
''Design mix'' ratios are decided by an engineer after analyzing the properties of the specific ingredients being used. Instead of using a 'nominal mix' of 1 part cement, 2 parts sand, and 4 parts aggregate, a civil engineer will custom-design a concrete mix to exactly meet the requirements of the site and conditions, setting material ratios and often designing an admixture package to fine-tune the properties or increase the performance envelope of the mix. Design-mix concrete can have very broad specifications that cannot be met with more basic nominal mixes, but the involvement of the engineer often increases the cost of the concrete mix.
Concrete mixes are primarily divided into nominal mix, standard mix and design mix.
Nominal mix ratios are given in volume of . Nominal mixes are a simple, fast way of getting a basic idea of the properties of the finished concrete without having to perform testing in advance.
Various governing bodies (such as British Standards) define nominal mix ratios into a number of grades, usually ranging from lower compressive strength to higher compressive strength. The grades usually indicate the 28-day cure strength.
Mixing
Thorough mixing is essential to produce uniform, high-quality concrete.
has shown that the mixing of cement and water into a paste before combining these materials with aggregates can increase the compressive strength of the resulting concrete. The paste is generally mixed in a , shear-type mixer at a w/c (water to cement ratio) of 0.30 to 0.45 by mass. The cement paste premix may include admixtures such as accelerators or retarders, superplasticizers, pigment
A pigment is a powder used to add or alter color or change visual appearance. Pigments are completely or nearly solubility, insoluble and reactivity (chemistry), chemically unreactive in water or another medium; in contrast, dyes are colored sub ...
s, or silica fume. The premixed paste is then blended with aggregates and any remaining batch water and final mixing is completed in conventional concrete mixing equipment.
Resonant acoustic mixing has also been found effective in producing ultra-high performance cementitious materials, as it produces a dense matrix with low porosity.
Sample analysis—workability
Workability is the ability of a fresh (plastic) concrete mix to fill the form/mold properly with the desired work (pouring, pumping, spreading, tamping, vibration) and without reducing the concrete's quality. Workability depends on water content, aggregate (shape and size distribution), cementitious content and age (level of hydration) and can be modified by adding chemical admixtures, like superplasticizer. Raising the water content or adding chemical admixtures increases concrete workability. Excessive water leads to increased bleeding or segregation of aggregates (when the cement and aggregates start to separate), with the resulting concrete having reduced quality. Changes in gradation can also affect workability of the concrete, although a wide range of gradation can be used for various applications. An undesirable gradation can mean using a large aggregate that is too large for the size of the formwork, or which has too few smaller aggregate grades to serve to fill the gaps between the larger grades, or using too little or too much sand for the same reason, or using too little water, or too much cement, or even using jagged crushed stone instead of smoother round aggregate such as pebbles. Any combination of these factors and others may result in a mix which is too harsh, i.e., which does not flow or spread out smoothly, is difficult to get into the formwork, and which is difficult to surface finish.
Workability can be measured by the concrete slump test, a simple measure of the plasticity of a fresh batch of concrete following the ASTM
ASTM International, formerly known as American Society for Testing and Materials, is a standards organization that develops and publishes voluntary consensus technical international standards for a wide range of materials, products, systems and s ...
C 143 or EN 12350-2 test standards. Slump is normally measured by filling an " Abrams cone" with a sample from a fresh batch of concrete. The cone is placed with the wide end down onto a level, non-absorptive surface. It is then filled in three layers of equal volume, with each layer being tamped with a steel rod to consolidate the layer. When the cone is carefully lifted off, the enclosed material slumps a certain amount, owing to gravity. A relatively dry sample slumps very little, having a slump value of out of . A relatively wet concrete sample may slump as much as . Workability can also be measured by the flow table test.
Slump can be increased by addition of chemical admixtures such as plasticizer or superplasticizer without changing the water-cement ratio. Some other admixtures, especially air-entraining admixture, can increase the slump of a mix.
High-flow concrete, like self-consolidating concrete, is tested by other flow-measuring methods. One of these methods includes placing the cone on the narrow end and observing how the mix flows through the cone while it is gradually lifted.
After mixing, concrete is a fluid and can be pumped to the location where needed.
Curing

Maintaining optimal conditions for cement hydration
Concrete must be kept moist during curing in order to achieve optimal strength and durability. During curing hydration occurs, allowing calcium-silicate hydrate (C-S-H) to form. Over 90% of a mix's final strength is typically reached within four weeks, with the remaining 10% achieved over years or even decades. The conversion of calcium hydroxide in the concrete into calcium carbonate from absorption of CO2 over several decades further strengthens the concrete and makes it more resistant to damage. This carbonation reaction, however, lowers the pH of the cement pore solution and can corrode the reinforcement bars.
Hydration and hardening of concrete during the first three days is critical. Abnormally fast drying and shrinkage due to factors such as evaporation from wind during placement may lead to increased tensile stresses at a time when it has not yet gained sufficient strength, resulting in greater shrinkage cracking. The early strength of the concrete can be increased if it is kept damp during the curing process. Minimizing stress prior to curing minimizes cracking. High-early-strength concrete is designed to hydrate faster, often by increased use of cement that increases shrinkage and cracking. The strength of concrete changes (increases) for up to three years. It depends on cross-section dimension of elements and conditions of structure exploitation.
Curing techniques avoiding water loss by evaporation
During the curing period, concrete is ideally maintained at controlled temperature and humidity. To ensure full hydration during curing, concrete slabs are often sprayed with "curing compounds" that create a water-retaining film over the concrete. Typical films are made of wax or related hydrophobic compounds. After the concrete is sufficiently cured, the film is allowed to abrade from the concrete through normal use.
Traditional conditions for curing involve spraying or ponding the concrete surface with water. The adjacent picture shows one of many ways to achieve this, ponding—submerging setting concrete in water and wrapping in plastic to prevent dehydration. Additional common curing methods include wet burlap and plastic sheeting covering the fresh concrete.
For higher-strength applications, accelerated curing techniques may be applied to the concrete. A common technique involves heating the poured concrete with steam, which serves to both keep it damp and raise the temperature so that the hydration process proceeds more quickly and more thoroughly.
Alternative types
Asphalt
''Asphalt concrete'' (commonly called ''asphalt'', ''blacktop'', or ''pavement'' in North America, and ''tarmac'', ''bitumen macadam'', or ''rolled asphalt'' in the United Kingdom
The United Kingdom of Great Britain and Northern Ireland, commonly known as the United Kingdom (UK) or Britain, is a country in Northwestern Europe, off the coast of European mainland, the continental mainland. It comprises England, Scotlan ...
and Ireland
Ireland (, ; ; Ulster Scots dialect, Ulster-Scots: ) is an island in the North Atlantic Ocean, in Northwestern Europe. Geopolitically, the island is divided between the Republic of Ireland (officially Names of the Irish state, named Irelan ...
) is a composite material
A composite or composite material (also composition material) is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a ...
commonly used to surface roads, parking lots, airport
An airport is an aerodrome with extended facilities, mostly for commercial Aviation, air transport. They usually consist of a landing area, which comprises an aerially accessible open space including at least one operationally active surf ...
s, as well as the core of embankment dams. Asphalt mixtures have been used in pavement construction since the beginning of the twentieth century. It consists of mineral aggregate bound together with asphalt, laid in layers, and compacted. The process was refined and enhanced by Belgian inventor and U.S. immigrant Edward De Smedt.
The terms ''asphalt'' (or ''asphaltic'') ''concrete'', ''bituminous asphalt concrete'', and ''bituminous mixture'' are typically used only in engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
and construction documents, which define concrete as any composite material composed of mineral aggregate adhered with a binder. The abbreviation, ''AC'', is sometimes used for ''asphalt concrete'' but can also denote ''asphalt content'' or ''asphalt cement'', referring to the liquid asphalt portion of the composite material.
Graphene enhanced concrete
Graphene enhanced concretes are standard designs of concrete mixes, except that during the cement-mixing or production process, a small amount of chemically engineered graphene is added. These enhanced graphene concretes are designed around the concrete application.
Microbial
Bacteria such as '' Bacillus pasteurii'', '' Bacillus pseudofirmus'', ''Bacillus cohnii'', ''Sporosarcina pasteuri'', and '' Arthrobacter crystallopoietes'' increase the compression strength of concrete through their biomass. However some forms of bacteria can also be concrete-destroying. Bacillus sp. CT-5. can reduce corrosion of reinforcement in reinforced concrete by up to four times. ''Sporosarcina pasteurii'' reduces water and chloride permeability. ''B. pasteurii'' increases resistance to acid. '' Bacillus pasteurii'' and ''B. sphaericuscan'' induce calcium carbonate precipitation in the surface of cracks, adding compression strength.
Nanoconcrete
 Nanoconcrete (also spelled "nano concrete"' or "nano-concrete") is a class of materials that contains Portland cement particles that are no greater than 100 μm and particles of silica no greater than 500 μm, which fill voids that would otherwise occur in normal concrete, thereby substantially increasing the material's strength. It is widely used in foot and highway bridges where high flexural and compressive strength are indicated.
Nanoconcrete (also spelled "nano concrete"' or "nano-concrete") is a class of materials that contains Portland cement particles that are no greater than 100 μm and particles of silica no greater than 500 μm, which fill voids that would otherwise occur in normal concrete, thereby substantially increasing the material's strength. It is widely used in foot and highway bridges where high flexural and compressive strength are indicated.[
]
Pervious
Pervious concrete is a mix of specially graded coarse aggregate, cement, water, and little-to-no fine aggregates. This concrete is also known as "no-fines" or porous concrete. Mixing the ingredients in a carefully controlled process creates a paste that coats and bonds the aggregate particles. The hardened concrete contains interconnected air voids totaling approximately 15 to 25 percent. Water runs through the voids in the pavement to the soil underneath. Air entrainment admixtures are often used in freeze-thaw climates to minimize the possibility of frost damage. Pervious concrete also permits rainwater to filter through roads and parking lots, to recharge aquifers, instead of contributing to runoff and flooding.
Polymer
Polymer concretes are mixtures of aggregate and any of various polymers and may be reinforced. The cement is costlier than lime-based cements, but polymer concretes nevertheless have advantages; they have significant tensile strength even without reinforcement, and they are largely impervious to water. Polymer concretes are frequently used for the repair and construction of other applications, such as drains.
Plant fibers
Plant fibers and particles can be used in a concrete mix or as a reinforcement. These materials can increase ductility but the lignocellulosic particles hydrolyze during concrete curing as a result of alkaline environment and elevated temperatures Such process, that is difficult to measure, can affect the properties of the resulting concrete.
Sulfur concrete
Sulfur concrete is a special concrete that uses sulfur as a binder and does not require cement or water.
Volcanic
Volcanic concrete substitutes volcanic rock for the limestone that is burned to form clinker. It consumes a similar amount of energy, but does not directly emit carbon as a byproduct. Volcanic rock/ash are used as supplementary cementitious materials in concrete to improve the resistance to sulfate, chloride and alkali silica reaction due to pore refinement. Also, they are generally cost effective in comparison to other aggregates,[ and good for thermal and acoustic insulation.][
Pyroclastic materials, such as pumice, scoria, and ashes are formed from cooling magma during explosive volcanic eruptions. They are used as supplementary cementitious materials (SCM) or as aggregates for cements and concretes. They have been extensively used since ancient times to produce materials for building applications. For example, pumice and other volcanic glasses were added as a natural pozzolanic material for mortars and plasters during the construction of the Villa San Marco in the Roman period (89 BC – 79 AD), which remain one of the best-preserved otium villae of the Bay of Naples in Italy.
]
Waste light
Waste light is a form of polymer modified concrete. The specific polymer admixture allows the replacement of all the traditional aggregates (gravel, sand, stone) by any mixture of solid waste materials in the grain size of 3–10 mm to form a low-compressive-strength (3–20 N/mm2) product for road and building construction. One cubic meter of waste light concrete contains 1.1–1.3 m3 of shredded waste and no other aggregates.
Recycled Aggregate Concrete (RAC)
Recycled aggregate concretes are standard concrete mixes with the addition or substitution of natural aggregates with recycled aggregates sourced from construction and demolition wastes, disused pre-cast concretes or masonry. In most cases, recycled aggregate concrete results in higher water absorption levels by capillary action and permeation, which are the prominent determiners of the strength and durability of the resulting concrete. The increase in water absorption levels is mainly caused by the porous adhered mortar that exists in the recycled aggregates. Accordingly, recycled concrete aggregates that have been washed to reduce the quantity of mortar adhered to aggregates show lower water absorption levels compared to untreated recycled aggregates.
The quality of the recycled aggregate concrete is determined by several factors, including the size, the number of replacement cycles, and the moisture levels of the recycled aggregates. When the recycled concrete aggregates are crushed into coarser fractures, the mixed concrete shows better permeability levels, resulting in an overall increase in strength. In contrast, recycled masonry aggregates provide better qualities when crushed in finer fractures. With each generation of recycled concrete, the resulting compressive strength decreases.
Properties
Concrete has relatively high compressive strength, but much lower tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or F_\text in notation) is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate ...
. Therefore, it is usually reinforced with materials that are strong in tension (often steel). The elasticity of concrete is relatively constant at low stress levels but starts decreasing at higher stress levels as matrix cracking develops. Concrete has a very low coefficient of thermal expansion and shrinks as it matures. All concrete structures crack to some extent, due to shrinkage and tension. Concrete that is subjected to long-duration forces is prone to creep.
Tests can be performed to ensure that the properties of concrete correspond to specifications for the application.
 The ingredients affect the strengths of the material. Concrete strength values are usually specified as the lower-bound compressive strength of either a cylindrical or cubic specimen as determined by standard test procedures.
The strengths of concrete is dictated by its function. Very low-strength— or less—concrete may be used when the concrete must be lightweight.
The ingredients affect the strengths of the material. Concrete strength values are usually specified as the lower-bound compressive strength of either a cylindrical or cubic specimen as determined by standard test procedures.
The strengths of concrete is dictated by its function. Very low-strength— or less—concrete may be used when the concrete must be lightweight.
Energy efficiency
The cement produced for making concrete accounts for about 8% of worldwide emissions per year (compared to, ''e.g.'', global aviation at 1.9%).limestone
Limestone is a type of carbonate rock, carbonate sedimentary rock which is the main source of the material Lime (material), lime. It is composed mostly of the minerals calcite and aragonite, which are different Polymorphism (materials science) ...
in the cement kiln (T ≈ 950 °C), and (2) from the combustion of fossil fuel to reach the sintering temperature (T ≈ 1450 °C) of cement clinker in the kiln. The energy required for extracting, crushing, and mixing the raw materials ( construction aggregates used in the concrete production, and also limestone
Limestone is a type of carbonate rock, carbonate sedimentary rock which is the main source of the material Lime (material), lime. It is composed mostly of the minerals calcite and aragonite, which are different Polymorphism (materials science) ...
and clay
Clay is a type of fine-grained natural soil material containing clay minerals (hydrous aluminium phyllosilicates, e.g. kaolinite, ). Most pure clay minerals are white or light-coloured, but natural clays show a variety of colours from impuriti ...
feeding the cement kiln) is lower. Energy requirement for transportation of ready-mix concrete is also lower because it is produced nearby the construction site from local resources, typically manufactured within 100 kilometers of the job site. The overall embodied energy of concrete at roughly 1 to 1.5 megajoules per kilogram is therefore lower than for many structural and construction materials.
Once in place, concrete offers a great energy efficiency over the lifetime of a building. Concrete walls leak air far less than those made of wood frames. Air leakage accounts for a large percentage of energy loss from a home. The thermal mass properties of concrete increase the efficiency of both residential and commercial buildings. By storing and releasing the energy needed for heating or cooling, concrete's thermal mass delivers year-round benefits by reducing temperature swings inside and minimizing heating and cooling costs.
Fire safety
Concrete buildings are more resistant to fire than those constructed using steel frames, since concrete has lower heat conductivity than steel and can thus last longer under the same fire conditions. Concrete is sometimes used as a fire protection for steel frames, for the same effect as above. Concrete as a fire shield, for example Fondu fyre, can also be used in extreme environments like a missile launch pad.
Options for non-combustible construction include floors, ceilings and roofs made of cast-in-place and hollow-core precast concrete. For walls, concrete masonry technology and Insulating Concrete Forms (ICFs) are additional options. ICFs are hollow blocks or panels made of fireproof insulating foam that are stacked to form the shape of the walls of a building and then filled with reinforced concrete to create the structure.
Concrete also provides good resistance against externally applied forces such as high winds, hurricanes, and tornadoes owing to its lateral stiffness, which results in minimal horizontal movement. However, this stiffness can work against certain types of concrete structures, particularly where a relatively higher flexing structure is required to resist more extreme forces.
Earthquake safety
As discussed above, concrete is very strong in compression, but weak in tension. Larger earthquakes can generate very large shear loads on structures. These shear loads subject the structure to both tensile and compressional loads. Concrete structures without reinforcement, like other unreinforced masonry structures, can fail during severe earthquake shaking. Unreinforced masonry structures constitute one of the largest earthquake risks globally. These risks can be reduced through seismic retrofitting of at-risk buildings, (e.g. school buildings in Istanbul, Turkey).
Construction
Concrete is one of the most durable building materials. It provides superior fire resistance compared with wooden construction and gains strength over time. Structures made of concrete can have a long service life. Concrete is used more than any other artificial material in the world.
Reinforced
 The use of reinforcement, in the form of iron was introduced in the 1850s by French industrialist François Coignet, and it was not until the 1880s that German civil engineer G. A. Wayss used steel as reinforcement. Concrete is a relatively brittle material that is strong under compression but less in tension. Plain, unreinforced concrete is unsuitable for many structures as it is relatively poor at withstanding stresses induced by vibrations, wind loading, and so on. Hence, to increase its overall strength, steel rods, wires, mesh or cables can be embedded in concrete before it is set. This reinforcement, often known as rebar, resists tensile forces.
The use of reinforcement, in the form of iron was introduced in the 1850s by French industrialist François Coignet, and it was not until the 1880s that German civil engineer G. A. Wayss used steel as reinforcement. Concrete is a relatively brittle material that is strong under compression but less in tension. Plain, unreinforced concrete is unsuitable for many structures as it is relatively poor at withstanding stresses induced by vibrations, wind loading, and so on. Hence, to increase its overall strength, steel rods, wires, mesh or cables can be embedded in concrete before it is set. This reinforcement, often known as rebar, resists tensile forces.
Precast
Precast concrete is concrete which is cast in one place for use elsewhere and is a mobile material. The largest part of precast production is carried out in the works of specialist suppliers, although in some instances, due to economic and geographical factors, scale of product or difficulty of access, the elements are cast on or adjacent to the construction site.
Mass structures
 Due to cement's exothermic chemical reaction while setting up, large concrete structures such as dams, navigation locks, large mat foundations, and large breakwaters generate excessive heat during hydration and associated expansion. To mitigate these effects, ''post-cooling''
Due to cement's exothermic chemical reaction while setting up, large concrete structures such as dams, navigation locks, large mat foundations, and large breakwaters generate excessive heat during hydration and associated expansion. To mitigate these effects, ''post-cooling''
Surface finishes
 Raw concrete surfaces tend to be porous and have a relatively uninteresting appearance. Many finishes can be applied to improve the appearance and preserve the surface against staining, water penetration, and freezing.
Examples of improved appearance include stamped concrete where the wet concrete has a pattern impressed on the surface, to give a paved, cobbled or brick-like effect, and may be accompanied with coloration. Another popular effect for flooring and table tops is polished concrete where the concrete is polished optically flat with diamond abrasives and sealed with polymers or other sealants.
Other finishes can be achieved with chiseling, or more conventional techniques such as painting or covering it with other materials.
The proper treatment of the surface of concrete, and therefore its characteristics, is an important stage in the construction and renovation of architectural structures.
Raw concrete surfaces tend to be porous and have a relatively uninteresting appearance. Many finishes can be applied to improve the appearance and preserve the surface against staining, water penetration, and freezing.
Examples of improved appearance include stamped concrete where the wet concrete has a pattern impressed on the surface, to give a paved, cobbled or brick-like effect, and may be accompanied with coloration. Another popular effect for flooring and table tops is polished concrete where the concrete is polished optically flat with diamond abrasives and sealed with polymers or other sealants.
Other finishes can be achieved with chiseling, or more conventional techniques such as painting or covering it with other materials.
The proper treatment of the surface of concrete, and therefore its characteristics, is an important stage in the construction and renovation of architectural structures.
Prestressed
 Prestressed concrete is a form of reinforced concrete that builds in compressive stresses during construction to oppose tensile stresses experienced in use. This can greatly reduce the weight of beams or slabs, by
better distributing the stresses in the structure to make optimal use of the reinforcement. For example, a horizontal beam tends to sag. Prestressed reinforcement along the bottom of the beam counteracts this.
In pre-tensioned concrete, the prestressing is achieved by using steel or polymer tendons or bars that are subjected to a tensile force prior to casting, or for post-tensioned concrete, after casting.
There are two different systems being used:
Prestressed concrete is a form of reinforced concrete that builds in compressive stresses during construction to oppose tensile stresses experienced in use. This can greatly reduce the weight of beams or slabs, by
better distributing the stresses in the structure to make optimal use of the reinforcement. For example, a horizontal beam tends to sag. Prestressed reinforcement along the bottom of the beam counteracts this.
In pre-tensioned concrete, the prestressing is achieved by using steel or polymer tendons or bars that are subjected to a tensile force prior to casting, or for post-tensioned concrete, after casting.
There are two different systems being used:precast concrete
Precast concrete is a construction product produced by casting concrete in a reusable molding (process), mold or "form" which is then cured in a controlled environment, transported to the construction site and maneuvered into place; examples i ...
are the most widely used types of concrete functional extensions in modern days. For more information see Brutalist architecture
Brutalist architecture is an architectural style that emerged during the 1950s in the United Kingdom, among the reconstruction projects of the post-war era. Brutalist buildings are characterised by Minimalism (art), minimalist constructions th ...
.
Placement
Once mixed, concrete is typically transported to the place where it is intended to become a structural item. Various methods of transportation and placement are used depending on the distances involve, quantity needed, and other details of application. Large amounts are often transported by truck, poured free under gravity or through a tremie, or pumped through a pipe. Smaller amounts may be carried in a skip (a metal container which can be tilted or opened to release the contents, usually transported by crane or hoist), or wheelbarrow, or carried in toggle bags for manual placement underwater.
Cold weather placement

Extreme weather
Extreme weather includes unexpected, unusual, severe weather, severe, or unseasonal weather; weather at the extremes of the historical distribution—the range that has been seen in the past. Extreme events are based on a location's recorded weat ...
conditions (extreme heat or cold; windy conditions, and humidity variations) can significantly alter the quality of concrete. Many precautions are observed in cold weather placement.Canada
Canada is a country in North America. Its Provinces and territories of Canada, ten provinces and three territories extend from the Atlantic Ocean to the Pacific Ocean and northward into the Arctic Ocean, making it the world's List of coun ...
, where temperatures tend to be much lower during the cold season, the following criteria are used by CSA A23.1:
* When the air temperature is ≤ 5 °C, and
* When there is a probability that the temperature may fall below 5 °C within 24 hours of placing the concrete.
The minimum strength before exposing concrete to extreme cold is . CSA A 23.1 specified a compressive strength of 7.0 MPa to be considered safe for exposure to freezing.
Underwater placement
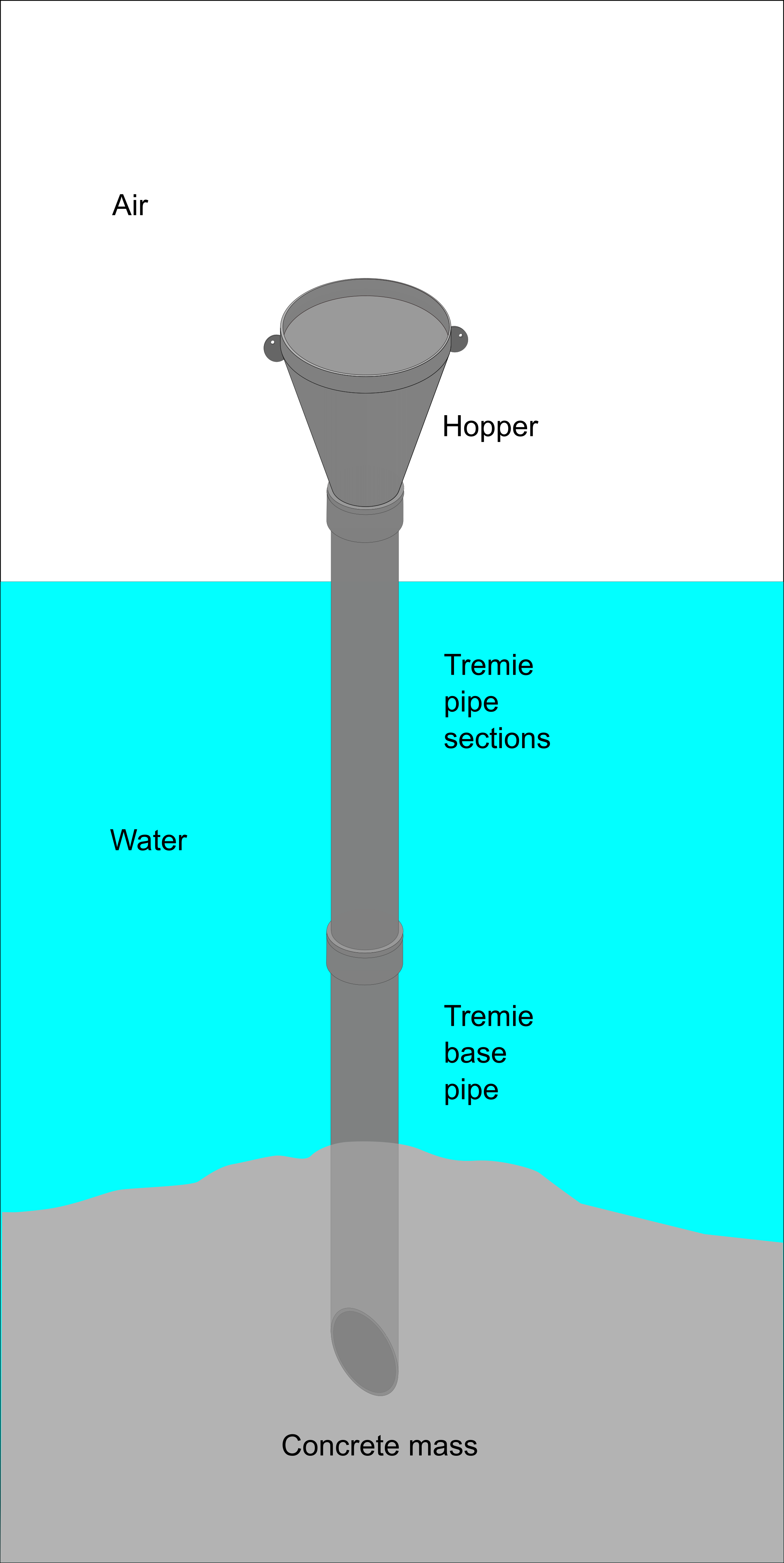 Concrete may be placed and cured underwater. Care must be taken in the placement method to prevent washing out the cement. Underwater placement methods include the tremie, pumping, skip placement, manual placement using toggle bags, and bagwork.
Concrete may be placed and cured underwater. Care must be taken in the placement method to prevent washing out the cement. Underwater placement methods include the tremie, pumping, skip placement, manual placement using toggle bags, and bagwork.
Roads
Concrete roads are more fuel efficient to drive on, more reflective and last significantly longer than other paving surfaces, yet have a much smaller market share than other paving solutions. Modern-paving methods and design practices have changed the economics of concrete paving, so that a well-designed and placed concrete pavement will be less expensive on initial costs and significantly less expensive over the life cycle. Another major benefit is that pervious concrete can be used, which eliminates the need to place storm drains near the road, and reducing the need for slightly sloped roadway to help rainwater to run off. No longer requiring discarding rainwater through use of drains also means that less electricity is needed (more pumping is otherwise needed in the water-distribution system), and no rainwater gets polluted as it no longer mixes with polluted water. Rather, it is immediately absorbed by the ground.
Tube forest
Cement molded into a forest of tubular structures can be 5.6 times more resistant to cracking/failure than standard concrete. The approach mimics mammalian cortical bone that features elliptical, hollow osteons suspended in an organic matrix, connected by relatively weak "cement lines". Cement lines provide a preferable in-plane crack path. This design fails via a "stepwise toughening mechanism". Cracks are contained within the tube, reducing spreading, by dissipating energy at each tube/step.
Environment, health and safety
The manufacture and use of concrete produce a wide range of environmental, economic and social impacts.
Health and safety
Grinding of concrete can produce hazardous dust. Exposure to cement dust can lead to issues such as silicosis, kidney disease, skin irritation and similar effects. The U.S. National Institute for Occupational Safety and Health in the United States recommends attaching local exhaust ventilation shrouds to electric concrete grinders to control the spread of this dust. In addition, the Occupational Safety and Health Administration (OSHA) has placed more stringent regulations on companies whose workers regularly come into contact with silica dust. An updated silica rule, which OSHA put into effect 23 September 2017 for construction companies, restricted the amount of breathable crystalline silica workers could legally come into contact with to 50 micro grams per cubic meter of air per 8-hour workday. That same rule went into effect 23 June 2018 for general industry, hydraulic fracturing and maritime. That deadline was extended to 23 June 2021 for engineering controls in the hydraulic fracturing industry. Companies which fail to meet the tightened safety regulations can face financial charges and extensive penalties. The presence of some substances in concrete, including useful and unwanted additives, can cause health concerns due to toxicity and radioactivity. Fresh concrete (before curing is complete) is highly alkaline and must be handled with proper protective equipment.
Cement
A major component of concrete is cement, a fine powder used mainly to bind sand and coarser aggregates together in concrete. Although a variety of cement types exist, the most common is " Portland cement", which is produced by mixing clinker with smaller quantities of other additives such as gypsum and ground limestone. The production of clinker, the main constituent of cement, is responsible for the bulk of the sector's greenhouse gas emissions, including both energy intensity and process emissions.
The cement industry is one of the three primary producers of carbon dioxide, a major greenhouse gas – the other two being energy production and transportation industries. On average, every tonne of cement produced releases one tonne of CO2 into the atmosphere. Pioneer cement manufacturers have claimed to reach lower carbon intensities, with 590 kg of CO2eq per tonne of cement produced. The emissions are due to combustion and calcination processes, which roughly account for 40% and 60% of the greenhouse gases, respectively. Considering that cement is only a fraction of the constituents of concrete, it is estimated that a tonne of concrete is responsible for emitting about 100–200 kg of CO2.surface runoff
Surface runoff (also known as overland flow or terrestrial runoff) is the unconfined flow of water over the ground surface, in contrast to ''channel runoff'' (or ''stream flow''). It occurs when excess rainwater, stormwater, meltwater, or other ...
, which can cause heavy soil erosion, water pollution, and flooding, but conversely can be used to divert, dam, and control flooding. Concrete dust released by building demolition
Demolition (also known as razing and wrecking) is the science and engineering in safely and efficiently tearing down buildings and other artificial structures. Demolition contrasts with deconstruction (building), deconstruction, which inv ...
and natural disasters can be a major source of dangerous air pollution
Air pollution is the presence of substances in the Atmosphere of Earth, air that are harmful to humans, other living beings or the environment. Pollutants can be Gas, gases like Ground-level ozone, ozone or nitrogen oxides or small particles li ...
. Concrete is a contributor to the urban heat island
Urban areas usually experience the urban heat island (UHI) effect; that is, they are significantly warmer than surrounding rural areas. The temperature difference is usually larger at night than during the day, and is most apparent when winds ar ...
effect, though less so than asphalt.
Climate change mitigation
Reducing the cement clinker content might have positive effects on the environmental life-cycle assessment of concrete. Some research work on reducing the cement clinker content in concrete has already been carried out. However, there exist different research strategies. Often replacement of some clinker for large amounts of slag or fly ash was investigated based on conventional concrete technology. This could lead to a waste of scarce raw materials such as slag and fly ash. The aim of other research activities is the efficient use of cement and reactive materials like slag and fly ash in concrete based on a modified mix design approach.
The embodied carbon of a precast concrete facade can be reduced by 50% when using the presented fiber reinforced high performance concrete in place of typical reinforced concrete cladding. Studies have been conducted about commercialization of low-carbon concretes. Life cycle assessment (LCA) of low-carbon concrete was investigated according to the ground granulated blast-furnace slag (GGBS) and fly ash (FA) replacement ratios. Global warming potential (GWP) of GGBS decreased by 1.1 kg CO2 eq/m3, while FA decreased by 17.3 kg CO2 eq/m3 when the mineral admixture replacement ratio was increased by 10%. This study also compared the compressive strength properties of binary blended low-carbon concrete according to the replacement ratios, and the applicable range of mixing proportions was derived.
Climate change adaptation
High-performance building materials will be particularly important for enhancing resilience, including for flood defenses and critical-infrastructure protection. Risks to infrastructure and cities posed by extreme weather events are especially serious for those places exposed to flood and hurricane damage, but also where residents need protection from extreme summer temperatures. Traditional concrete can come under strain when exposed to humidity and higher concentrations of atmospheric CO2. While concrete is likely to remain important in applications where the environment is challenging, novel, smarter and more adaptable materials are also needed.
End-of-life: degradation and waste
Recycling
There have been concerns about the recycling of painted concrete due to possible lead content. Studies have indicated that recycled concrete exhibits lower strength and durability compared to concrete produced using natural aggregates. This deficiency can be addressed by incorporating supplementary materials such as fly ash into the mixture.
World records
The world record for the largest concrete pour in a single project is the Three Gorges Dam in Hubei Province, China by the Three Gorges Corporation. The amount of concrete used in the construction of the dam is estimated at 16 million cubic meters over 17 years. The previous record was 12.3 million cubic meters held by Itaipu hydropower station in Brazil.Himachal Pradesh
Himachal Pradesh (; Sanskrit: ''himācāl prādes;'' "Snow-laden Mountain Province") is a States and union territories of India, state in the northern part of India. Situated in the Western Himalayas, it is one of the thirteen Indian Himalayan ...
, India, when the concrete mix was pumped through a vertical height of .
The Polavaram dam works in Andhra Pradesh
Andhra Pradesh (ISO 15919, ISO: , , AP) is a States and union territories of India, state on the East Coast of India, east coast of southern India. It is the List of states and union territories of India by area, seventh-largest state and th ...
on 6 January 2019 entered the Guinness World Records
''Guinness World Records'', known from its inception in 1955 until 1999 as ''The Guinness Book of Records'' and in previous United States editions as ''The Guinness Book of World Records'', is a British reference book published annually, list ...
by pouring 32,100 cubic metres of concrete in 24 hours. The world record for the largest continuously poured concrete raft was achieved in August 2007 in Abu Dhabi by contracting firm Al Habtoor-CCC Joint Venture and the concrete supplier is Unibeton Ready Mix.Kuala Lumpur
Kuala Lumpur (KL), officially the Federal Territory of Kuala Lumpur, is the capital city and a Federal Territories of Malaysia, federal territory of Malaysia. It is the largest city in the country, covering an area of with a census population ...
, Malaysia.
The world record for largest continuously poured concrete floor was completed 8 November 1997, in Louisville, Kentucky by design-build firm EXXCEL Project Management. The monolithic placement consisted of of concrete placed in 30 hours, finished to a flatness tolerance of FF 54.60 and a levelness tolerance of FL 43.83. This surpassed the previous record by 50% in total volume and 7.5% in total area.
The record for the largest continuously placed underwater concrete pour was completed 18 October 2010, in New Orleans, Louisiana by contractor C. J. Mahan Construction Company, LLC of Grove City, Ohio. The placement consisted of 10,251 cubic yards of concrete placed in 58.5 hours using two concrete pumps and two dedicated concrete batch plants. Upon curing, this placement allows the cofferdam to be dewatered approximately below sea level to allow the construction of the Inner Harbor Navigation Canal Sill & Monolith Project to be completed in the dry.
Art
Concrete is used as an artistic medium.
See also
*
*
*
*
* Eurocode 2: Design of concrete structures
*
*
*
*
*
*
References
Further reading
*
External links
Advantage and Disadvantage of Concrete
*
*
Release of ultrafine particles from three simulated building processes
* Concrete
The Quest for Greener Alternatives
{{Authority control
Building materials
Composite materials
Heterogeneous chemical mixtures
Masonry
Pavements
Roofing materials
Sculpture materials
Articles containing video clips
 Concrete is a
Concrete is a  Construction aggregates consist of large chunks of material in a concrete mix, generally a coarse gravel or crushed rocks such as
Construction aggregates consist of large chunks of material in a concrete mix, generally a coarse gravel or crushed rocks such as 
 Nanoconcrete (also spelled "nano concrete"' or "nano-concrete") is a class of materials that contains Portland cement particles that are no greater than 100 μm and particles of silica no greater than 500 μm, which fill voids that would otherwise occur in normal concrete, thereby substantially increasing the material's strength. It is widely used in foot and highway bridges where high flexural and compressive strength are indicated.
Nanoconcrete (also spelled "nano concrete"' or "nano-concrete") is a class of materials that contains Portland cement particles that are no greater than 100 μm and particles of silica no greater than 500 μm, which fill voids that would otherwise occur in normal concrete, thereby substantially increasing the material's strength. It is widely used in foot and highway bridges where high flexural and compressive strength are indicated.
 The ingredients affect the strengths of the material. Concrete strength values are usually specified as the lower-bound compressive strength of either a cylindrical or cubic specimen as determined by standard test procedures.
The strengths of concrete is dictated by its function. Very low-strength— or less—concrete may be used when the concrete must be lightweight. Lightweight concrete is often achieved by adding air, foams, or lightweight aggregates, with the side effect that the strength is reduced. For most routine uses, concrete is often used. concrete is readily commercially available as a more durable, although more expensive, option. Higher-strength concrete is often used for larger civil projects. Strengths above are often used for specific building elements. For example, the lower floor columns of high-rise concrete buildings may use concrete of or more, to keep the size of the columns small. Bridges may use long beams of high-strength concrete to lower the number of spans required. Occasionally, other structural needs may require high-strength concrete. If a structure must be very rigid, concrete of very high strength may be specified, even much stronger than is required to bear the service loads. Strengths as high as have been used commercially for these reasons.
The ingredients affect the strengths of the material. Concrete strength values are usually specified as the lower-bound compressive strength of either a cylindrical or cubic specimen as determined by standard test procedures.
The strengths of concrete is dictated by its function. Very low-strength— or less—concrete may be used when the concrete must be lightweight. Lightweight concrete is often achieved by adding air, foams, or lightweight aggregates, with the side effect that the strength is reduced. For most routine uses, concrete is often used. concrete is readily commercially available as a more durable, although more expensive, option. Higher-strength concrete is often used for larger civil projects. Strengths above are often used for specific building elements. For example, the lower floor columns of high-rise concrete buildings may use concrete of or more, to keep the size of the columns small. Bridges may use long beams of high-strength concrete to lower the number of spans required. Occasionally, other structural needs may require high-strength concrete. If a structure must be very rigid, concrete of very high strength may be specified, even much stronger than is required to bear the service loads. Strengths as high as have been used commercially for these reasons.
 Due to cement's exothermic chemical reaction while setting up, large concrete structures such as dams, navigation locks, large mat foundations, and large breakwaters generate excessive heat during hydration and associated expansion. To mitigate these effects, ''post-cooling'' is commonly applied during construction. An early example at Hoover Dam used a network of pipes between vertical concrete placements to circulate cooling water during the curing process to avoid damaging overheating. Similar systems are still used; depending on volume of the pour, the concrete mix used, and ambient air temperature, the cooling process may last for many months after the concrete is placed. Various methods also are used to pre-cool the concrete mix in mass concrete structures.
Another approach to mass concrete structures that minimizes cement's thermal by-product is the use of roller-compacted concrete, which uses a dry mix which has a much lower cooling requirement than conventional wet placement. It is deposited in thick layers as a semi-dry material then roller compacted into a dense, strong mass.
Due to cement's exothermic chemical reaction while setting up, large concrete structures such as dams, navigation locks, large mat foundations, and large breakwaters generate excessive heat during hydration and associated expansion. To mitigate these effects, ''post-cooling'' is commonly applied during construction. An early example at Hoover Dam used a network of pipes between vertical concrete placements to circulate cooling water during the curing process to avoid damaging overheating. Similar systems are still used; depending on volume of the pour, the concrete mix used, and ambient air temperature, the cooling process may last for many months after the concrete is placed. Various methods also are used to pre-cool the concrete mix in mass concrete structures.
Another approach to mass concrete structures that minimizes cement's thermal by-product is the use of roller-compacted concrete, which uses a dry mix which has a much lower cooling requirement than conventional wet placement. It is deposited in thick layers as a semi-dry material then roller compacted into a dense, strong mass.
 Raw concrete surfaces tend to be porous and have a relatively uninteresting appearance. Many finishes can be applied to improve the appearance and preserve the surface against staining, water penetration, and freezing.
Examples of improved appearance include stamped concrete where the wet concrete has a pattern impressed on the surface, to give a paved, cobbled or brick-like effect, and may be accompanied with coloration. Another popular effect for flooring and table tops is polished concrete where the concrete is polished optically flat with diamond abrasives and sealed with polymers or other sealants.
Other finishes can be achieved with chiseling, or more conventional techniques such as painting or covering it with other materials.
The proper treatment of the surface of concrete, and therefore its characteristics, is an important stage in the construction and renovation of architectural structures.
Raw concrete surfaces tend to be porous and have a relatively uninteresting appearance. Many finishes can be applied to improve the appearance and preserve the surface against staining, water penetration, and freezing.
Examples of improved appearance include stamped concrete where the wet concrete has a pattern impressed on the surface, to give a paved, cobbled or brick-like effect, and may be accompanied with coloration. Another popular effect for flooring and table tops is polished concrete where the concrete is polished optically flat with diamond abrasives and sealed with polymers or other sealants.
Other finishes can be achieved with chiseling, or more conventional techniques such as painting or covering it with other materials.
The proper treatment of the surface of concrete, and therefore its characteristics, is an important stage in the construction and renovation of architectural structures.
 Prestressed concrete is a form of reinforced concrete that builds in compressive stresses during construction to oppose tensile stresses experienced in use. This can greatly reduce the weight of beams or slabs, by
better distributing the stresses in the structure to make optimal use of the reinforcement. For example, a horizontal beam tends to sag. Prestressed reinforcement along the bottom of the beam counteracts this.
In pre-tensioned concrete, the prestressing is achieved by using steel or polymer tendons or bars that are subjected to a tensile force prior to casting, or for post-tensioned concrete, after casting.
There are two different systems being used:
* Pretensioned concrete is almost always precast, and contains steel wires (tendons) that are held in tension while the concrete is placed and sets around them.
* Post-tensioned concrete has ducts through it. After the concrete has gained strength, tendons are pulled through the ducts and stressed. The ducts are then filled with grout. Bridges built in this way have experienced considerable corrosion of the tendons, so external post-tensioning may now be used in which the tendons run along the outer surface of the concrete.
More than of highways in the United States are paved with this material. Reinforced concrete, prestressed concrete and
Prestressed concrete is a form of reinforced concrete that builds in compressive stresses during construction to oppose tensile stresses experienced in use. This can greatly reduce the weight of beams or slabs, by
better distributing the stresses in the structure to make optimal use of the reinforcement. For example, a horizontal beam tends to sag. Prestressed reinforcement along the bottom of the beam counteracts this.
In pre-tensioned concrete, the prestressing is achieved by using steel or polymer tendons or bars that are subjected to a tensile force prior to casting, or for post-tensioned concrete, after casting.
There are two different systems being used:
* Pretensioned concrete is almost always precast, and contains steel wires (tendons) that are held in tension while the concrete is placed and sets around them.
* Post-tensioned concrete has ducts through it. After the concrete has gained strength, tendons are pulled through the ducts and stressed. The ducts are then filled with grout. Bridges built in this way have experienced considerable corrosion of the tendons, so external post-tensioning may now be used in which the tendons run along the outer surface of the concrete.
More than of highways in the United States are paved with this material. Reinforced concrete, prestressed concrete and 
 Concrete may be placed and cured underwater. Care must be taken in the placement method to prevent washing out the cement. Underwater placement methods include the tremie, pumping, skip placement, manual placement using toggle bags, and bagwork.
A tremie is a vertical, or near-vertical, pipe with a hopper at the top used to pour concrete underwater in a way that avoids washout of cement from the mix due to turbulent water contact with the concrete while it is flowing. This produces a more reliable strength of the product. The method is generally used for placing small quantities and for repairs. Wet concrete is loaded into a reusable canvas bag and squeezed out at the required place by the diver. Care must be taken to avoid washout of the cement and fines.
is the manual placement by divers of woven cloth bags containing dry mix, followed by piercing the bags with steel rebar pins to tie the bags together after every two or three layers, and create a path for hydration to induce curing, which can typically take about 6 to 12 hours for initial hardening and full hardening by the next day. Bagwork concrete will generally reach full strength within 28 days. Each bag must be pierced by at least one, and preferably up to four pins. Bagwork is a simple and convenient method of underwater concrete placement which does not require pumps, plant, or formwork, and which can minimise environmental effects from dispersing cement in the water. Prefilled bags are available, which are sealed to prevent premature hydration if stored in suitable dry conditions. The bags may be biodegradable.
is an alternative method of forming a concrete mass underwater, where the forms are filled with coarse aggregate and the voids then completely filled from the bottom by displacing the water with pumped grout.
Concrete may be placed and cured underwater. Care must be taken in the placement method to prevent washing out the cement. Underwater placement methods include the tremie, pumping, skip placement, manual placement using toggle bags, and bagwork.
A tremie is a vertical, or near-vertical, pipe with a hopper at the top used to pour concrete underwater in a way that avoids washout of cement from the mix due to turbulent water contact with the concrete while it is flowing. This produces a more reliable strength of the product. The method is generally used for placing small quantities and for repairs. Wet concrete is loaded into a reusable canvas bag and squeezed out at the required place by the diver. Care must be taken to avoid washout of the cement and fines.
is the manual placement by divers of woven cloth bags containing dry mix, followed by piercing the bags with steel rebar pins to tie the bags together after every two or three layers, and create a path for hydration to induce curing, which can typically take about 6 to 12 hours for initial hardening and full hardening by the next day. Bagwork concrete will generally reach full strength within 28 days. Each bag must be pierced by at least one, and preferably up to four pins. Bagwork is a simple and convenient method of underwater concrete placement which does not require pumps, plant, or formwork, and which can minimise environmental effects from dispersing cement in the water. Prefilled bags are available, which are sealed to prevent premature hydration if stored in suitable dry conditions. The bags may be biodegradable.
is an alternative method of forming a concrete mass underwater, where the forms are filled with coarse aggregate and the voids then completely filled from the bottom by displacing the water with pumped grout.