5 1 Channels (surround Sound) Label on:
[Wikipedia]
[Google]
[Amazon]
5 (five) is a
 is the third smallest
is the third smallest
 A
A
"Cubic Symmetric Graphs (The Foster Census)."
The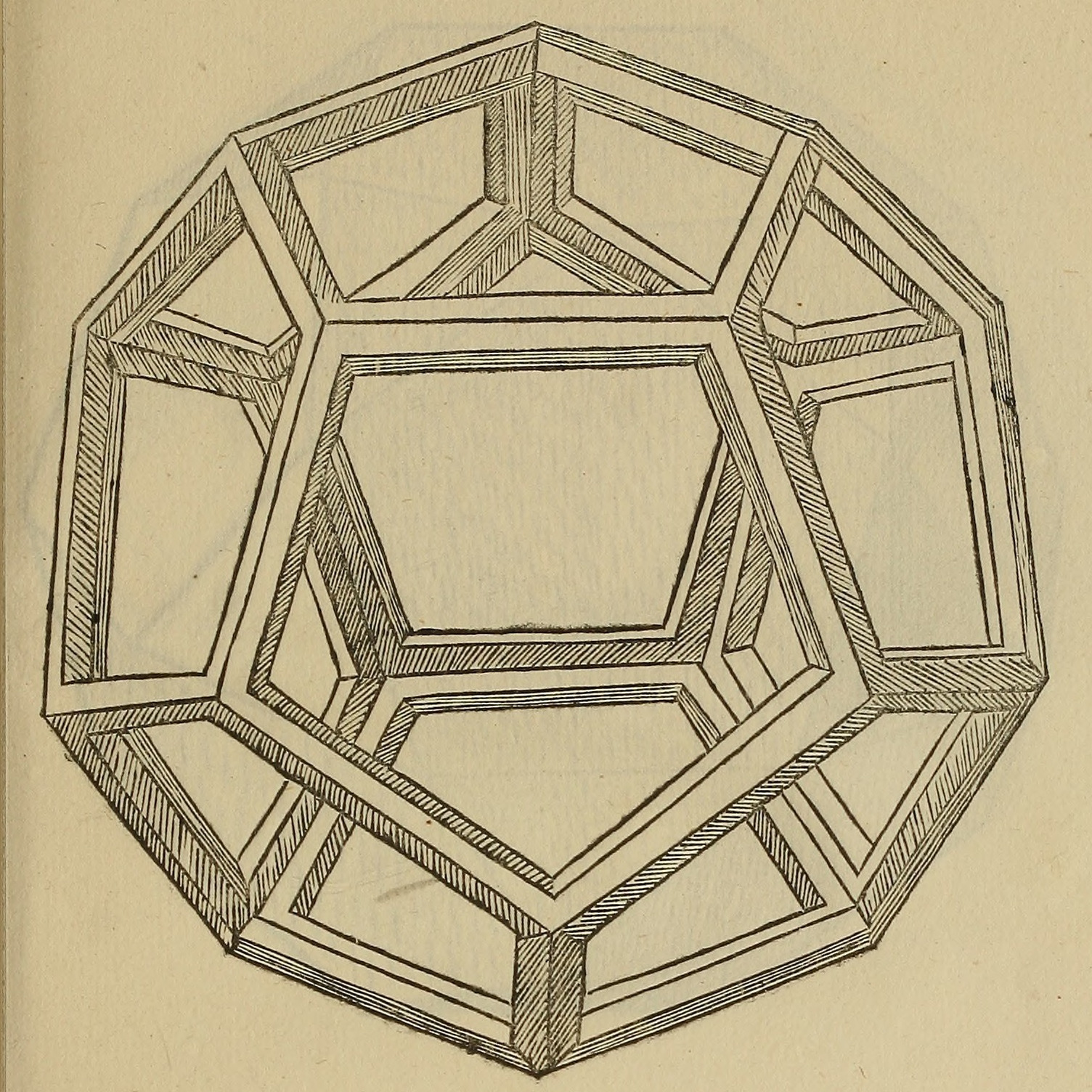 There are
There are

 The evolution of the modern Western digit for the numeral 5 cannot be traced back to the
The evolution of the modern Western digit for the numeral 5 cannot be traced back to the
The Number 5The Positive Integer 5
{{DEFAULTSORT:5 (Number) Integers 5 (number)
number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers c ...
, numeral and digit. It is the natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''Cardinal n ...
, and cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality (size) of sets. The cardinality of a finite set is a natural number: the number of elements in the set. Th ...
, following 4 and preceding 6, and is a prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
. It has attained significance throughout history in part because typical humans have five digits on each hand.
In mathematics
prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
, and the second super-prime
Super-prime numbers, also known as higher-order primes or prime-indexed primes (PIPs), are the subsequence of prime numbers that occupy prime-numbered positions within the sequence of all prime numbers.
The subsequence begins
:3, 5, 11, 17, 31, ...
. It is the first safe prime
In number theory, a prime number ''p'' is a if 2''p'' + 1 is also prime. The number 2''p'' + 1 associated with a Sophie Germain prime is called a . For example, 11 is a Sophie Germain prime and 2 × 11 + ...
, the first good prime A good prime is a prime number whose square is greater than the product of any two primes at the same number of positions before and after it in the sequence of primes.
That is, good prime satisfies the inequality
:p_n^2 > p_ \cdot p_
for all 1 � ...
, the first balanced prime In number theory, a balanced prime is a prime number with equal-sized prime gaps above and below it, so that it is equal to the arithmetic mean of the nearest primes above and below. Or to put it algebraically, given a prime number p_n, where is it ...
, and the first of three known Wilson prime
In number theory, a Wilson prime is a prime number p such that p^2 divides (p-1)!+1, where "!" denotes the factorial function; compare this with Wilson's theorem, which states that every prime p divides (p-1)!+1. Both are named for 18th-century E ...
s. Five is the second Fermat prime
In mathematics, a Fermat number, named after Pierre de Fermat, who first studied them, is a positive integer of the form
:F_ = 2^ + 1,
where ''n'' is a non-negative integer. The first few Fermat numbers are:
: 3, 5, 17, 257, 65537, 4294967 ...
and the third Mersenne prime
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form for some integer . They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17t ...
exponent, as well as the third Catalan number
In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles Cata ...
, and the third Sophie Germain prime
In number theory, a prime number ''p'' is a if 2''p'' + 1 is also prime. The number 2''p'' + 1 associated with a Sophie Germain prime is called a . For example, 11 is a Sophie Germain prime and 2 × 11 + ...
. Notably, 5 is equal to the sum of the ''only'' consecutive primes, 2 + 3, and is the only number that is part of more than one pair of twin prime
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair (41, 43). In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term ''twin pr ...
s, ( 3, 5) and (5, 7). It is also a sexy prime
In number theory, sexy primes are prime numbers that differ from each other by 6. For example, the numbers 5 and 11 are both sexy primes, because both are prime and .
The term "sexy prime" is a pun stemming from the Latin word for six: .
If o ...
with the fifth prime number and first prime repunit, 11. Five is the third factorial prime
A factorial prime is a prime number that is one less or one more than a factorial (all factorials greater than 1 are even).
The first 10 factorial primes (for ''n'' = 1, 2, 3, 4, 6, 7, 11, 12, 14) are :
: 2 (0! +&n ...
, an alternating factorial, and an Eisenstein prime
In mathematics, an Eisenstein prime is an Eisenstein integer
: z = a + b\,\omega, \quad \text \quad \omega = e^,
that is irreducible (or equivalently prime) in the ring-theoretic sense: its only Eisenstein divisors are the units , itself ...
with no imaginary part and real part of the form − . In particular, five is the first congruent number
In number theory, a congruent number is a positive integer that is the area of a right triangle with three rational number sides. A more general definition includes all positive rational numbers with this property.
The sequence of (integer) cong ...
, since it is the length of the hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equa ...
of the smallest integer-sided right triangle.
Five is the second Fermat prime
In mathematics, a Fermat number, named after Pierre de Fermat, who first studied them, is a positive integer of the form
:F_ = 2^ + 1,
where ''n'' is a non-negative integer. The first few Fermat numbers are:
: 3, 5, 17, 257, 65537, 4294967 ...
of the form + , and more generally the second Sierpiński number of the first kind, + . There are a total of five known Fermat primes, which also include 3, 17, 257, and 65537
65537 is the integer after 65536 and before 65538.
In mathematics
65537 is the largest known prime number of the form 2^ +1 (n = 4). Therefore, a regular polygon with 65537 sides is constructible with compass and unmarked straightedge. Johann ...
. The sum of the first 3 Fermat primes, 3, 5 and 17, yields 25 or 52, while 257 is the 55th prime number. Combinations from these 5 Fermat primes generate 31 polygons with an odd
Odd means unpaired, occasional, strange or unusual, or a person who is viewed as eccentric.
Odd may also refer to:
Acronym
* ODD (Text Encoding Initiative) ("One Document Does it all"), an abstracted literate-programming format for describing X ...
number of sides that can be construncted purely with a compass and straight-edge, which includes the five-sided regular pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
. Apropos, 31 is also equal to the sum of the maximum number of area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape
A shape or figure is a graphics, graphical representation of an obje ...
s inside a circle that are formed from the sides and diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek δ ...
s of the first five -sided polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed ''polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two toge ...
s, and equal to the maximum number of areas formed by a six-sided polygon; per Moser's circle problem.
The number 5 is the fifth Fibonacci number
In mathematics, the Fibonacci numbers, commonly denoted , form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors start the sequence from ...
, being 2 plus 3. It is the only Fibonacci number that is equal to its position aside from 1, which is both the first and second Fibonacci numbers. Five is also a Pell number
In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins , , , , an ...
and a Markov number
A Markov number or Markoff number is a positive integer ''x'', ''y'' or ''z'' that is part of a solution to the Markov Diophantine equation
:x^2 + y^2 + z^2 = 3xyz,\,
studied by .
The first few Markov numbers are
: 1, 2, 5, 13, 29, 34, 89 ...
, appearing in solutions to the Markov Diophantine equation: (1, 2, 5), (1, 5, 13), (2, 5, 29), (5, 13, 194), (5, 29, 433), ... ( lists Markov numbers that appear in solutions where one of the other two terms is 5). Whereas 5 is unique in the Fibonacci sequence, in the Perrin sequence 5 is both the fifth and sixth Perrin number
In mathematics, the Perrin numbers are defined by the recurrence relation
: for ,
with initial values
:.
The sequence of Perrin numbers starts with
: 3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, ...
The number of different maxima ...
s.
5 is the third Mersenne prime exponent of the form − , which yields : the prime index of the third Mersenne prime
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form for some integer . They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17t ...
and second double Mersenne prime
In mathematics, a double Mersenne number is a Mersenne number of the form
:M_ = 2^-1
where ''p'' is prime.
Examples
The first four terms of the sequence of double Mersenne numbers areChris Caldwell''Mersenne Primes: History, Theorems and Li ...
127, as well as the third double Mersenne prime exponent for the number 2,147,483,647
The number 2,147,483,647 is the eighth Mersenne prime, equal to 231 − 1. It is one of only four known double Mersenne primes.
The primality of this number was proven by Leonhard Euler, who reported the proof in a letter to Daniel ...
, which is the largest value that a signed 32-bit
In computer architecture, 32-bit computing refers to computer systems with a processor, memory, and other major system components that operate on data in 32-bit units. Compared to smaller bit widths, 32-bit computers can perform large calculation ...
integer field can hold. There are only four known double Mersenne prime numbers, with a fifth candidate double Mersenne prime = 223058...93951 − 1 too large to compute with current computers. In a related sequence, the first 5 terms in the sequence of Catalan–Mersenne numbers are the only known prime terms, with a sixth possible candidate in the order of 101037.7094. These prime sequences are conjectured to be prime up to a certain limit.
Every odd number greater than is the sum of at most five prime numbers, and every odd number greater than is conjectured to be expressible as the sum of three prime numbers. Helfgtott has provided a proof of the latter, also known as the odd Goldbach conjecture
In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, states that
: Every odd number greater than 5 can be expressed as the sum of three prime number, prime ...
, that is already widely acknowledged by mathematicians as it still undergoes peer-review
Peer review is the evaluation of work by one or more people with similar competencies as the producers of the work (peers). It functions as a form of self-regulation by qualified members of a profession within the relevant field. Peer review ...
.
The sums of the first five non-primes greater than zero + + + + and the first five prime numbers + + + + both equal ; the 7th triangular number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
and like a perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number.
T ...
, which also includes , the 31st triangular number and perfect number of the form −1( − ) with a of , by the Euclid–Euler theorem
The Euclid–Euler theorem is a theorem in number theory that relates perfect numbers to Mersenne primes. It states that an even number is perfect if and only if it has the form , where is a prime number. The theorem is named after mathematician ...
.
There are a total of five known unitary perfect number
A unitary perfect number is an integer which is the sum of its positive proper unitary divisors, not including the number itself (a divisor ''d'' of a number ''n'' is a unitary divisor if ''d'' and ''n''/''d'' share no common factors). Some perfect ...
s, which are numbers that are the sums of their positive proper
Proper may refer to:
Mathematics
* Proper map, in topology, a property of continuous function between topological spaces, if inverse images of compact subsets are compact
* Proper morphism, in algebraic geometry, an analogue of a proper map for ...
unitary divisor In mathematics, a natural number ''a'' is a unitary divisor (or Hall divisor) of a number ''b'' if ''a'' is a divisor of ''b'' and if ''a'' and \frac are coprime, having no common factor other than 1. Thus, 5 is a unitary divisor of 60, because 5 an ...
s. A sixth unitary number, if discovered, would have at least nine odd prime factors.
Five is conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis (still a conjecture) or Fermat's Last Theorem (a conjecture until proven in 19 ...
d to be the only odd untouchable number
An untouchable number is a positive integer that cannot be expressed as the sum of all the proper divisors of any positive integer (including the untouchable number itself). That is, these numbers are not in the image of the aliquot sum function. ...
, and if this is the case then five will be the only odd prime number that is not the base of an aliquot tree.
In figurate number
The term figurate number is used by different writers for members of different sets of numbers, generalizing from triangular numbers to different shapes (polygonal numbers) and different dimensions (polyhedral numbers). The term can mean
* polygon ...
s, 5 is a pentagonal number
A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical. The ...
, with the sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is calle ...
of pentagonal numbers starting: 1, 5, 12, 22, 35, ...
* 5 is a centered tetrahedral number
A centered tetrahedral number is a centered figurate number that represents a tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, ...
: 1, 5, 15, 35, 69, ... Every centered tetrahedral number with an index of 2, 3 or 4 modulo 5 is divisible by 5.
* 5 is a square pyramidal number
In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the number of stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broa ...
: 1, 5, 14, 30, 55, ... The sum of the first four members is 50 while the fifth indexed member in the sequence is 55.
* 5 is a centered square number
In elementary number theory, a centered square number is a centered figurate number that gives the number of dots in a square with a dot in the center and all other dots surrounding the center dot in successive square layers. That is, each cen ...
: 1, 5, 13, 25, 41, ... The fifth square number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals ...
or 52 is 25, which features in the proportions of the two smallest (3, 4, 5) and (5, 12, 13) ''primitive'' Pythagorean triple
A Pythagorean triple consists of three positive integers , , and , such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer . A primitive Pythagorean triple is ...
s.
The factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
of five, or ! = , is the sum of the first fifteen non-zero positive integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s, and 15th triangular number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
, which in turn is the sum of the first five non-zero positive integers and 5th triangular number. 35, which is the fourth or fifth pentagonal and tetrahedral number
A tetrahedral number, or triangular pyramidal number, is a figurate number that represents a pyramid with a triangular base and three sides, called a tetrahedron. The th tetrahedral number, , is the sum of the first triangular numbers, that is,
...
, is equal to the sum of the first five triangular numbers: 1, 3, 6, 10, 15.
5 is the value of the central cell
Cell most often refers to:
* Cell (biology), the functional basic unit of life
Cell may also refer to:
Locations
* Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery ...
of the only non-trivial normal magic square, also called the ''Lo Shu'' square. Its x array of squares has a magic constant
The magic constant or magic sum of a magic square is the sum of numbers in any row, column, or diagonal of the magic square. For example, the magic square shown below has a magic constant of 15. For a normal magic square of order ''n'' – that is ...
of , where the sums of its rows, columns, and diagonals are all equal to fifteen. 5 is also the value of the central cell the only non-trivial order-3 normal magic hexagon that is made of nineteen cells.
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An exa ...
equations of degree and below can be solved with radicals, while quintic equation
In algebra, a quintic function is a function of the form
:g(x)=ax^5+bx^4+cx^3+dx^2+ex+f,\,
where , , , , and are members of a field, typically the rational numbers, the real numbers or the complex numbers, and is nonzero. In other words, a q ...
s of degree 5, and higher, cannot generally be so solved. This is the Abel–Ruffini theorem
In mathematics, the Abel–Ruffini theorem (also known as Abel's impossibility theorem) states that there is no solution in radicals to general polynomial equations of degree five or higher with arbitrary coefficients. Here, ''general'' means th ...
. This is related to the fact that the symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group \m ...
is a solvable group
In mathematics, more specifically in the field of group theory, a solvable group or soluble group is a group that can be constructed from abelian groups using extensions. Equivalently, a solvable group is a group whose derived series terminates ...
for ''n'' ⩽ 4 and not solvable for ''n'' ⩾ 5.
Euler's identity
In mathematics, Euler's identity (also known as Euler's equation) is the equality
e^ + 1 = 0
where
: is Euler's number, the base of natural logarithms,
: is the imaginary unit, which by definition satisfies , and
: is pi, the ratio of the circ ...
, + = , contains five essential number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers c ...
s used widely in mathematics: Archimedes' constant , Euler's number
The number , also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of a logarithm, base of the natural logarithms. It is the Limit of a sequence, limit ...
, the imaginary number
An imaginary number is a real number multiplied by the imaginary unit , is usually used in engineering contexts where has other meanings (such as electrical current) which is defined by its property . The square of an imaginary number is . Fo ...
, unity
Unity may refer to:
Buildings
* Unity Building, Oregon, Illinois, US; a historic building
* Unity Building (Chicago), Illinois, US; a skyscraper
* Unity Buildings, Liverpool, UK; two buildings in England
* Unity Chapel, Wyoming, Wisconsin, US; a h ...
, and zero
0 (zero) is a number representing an empty quantity. In place-value notation
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or ...
, which makes this formula a renown example of beauty in mathematics.
In geometry
pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle aroun ...
, or five-pointed polygram
PolyGram N.V. was a multinational entertainment company and major music record label formerly based in the Netherlands. It was founded in 1962 as the Grammophon-Philips Group by Dutch corporation Philips and German corporation Siemens, to be a ...
, is the first proper star polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations ...
constructed from the diagonals of a regular pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
as self-intersecting edges that are proportioned in golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0,
where the Greek letter phi ( ...
, . Its internal geometry appears prominently in Penrose tilings, and is a facet
Facets () are flat faces on geometric shapes. The organization of naturally occurring facets was key to early developments in crystallography, since they reflect the underlying symmetry of the crystal structure. Gemstones commonly have facets cut ...
inside Kepler-Poinsot star polyhedra and Schläfli–Hess star polychora, represented by its Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
. A similar figure to the pentagram is a five-pointed simple
Simple or SIMPLE may refer to:
*Simplicity, the state or quality of being simple
Arts and entertainment
* ''Simple'' (album), by Andy Yorke, 2008, and its title track
* "Simple" (Florida Georgia Line song), 2018
* "Simple", a song by Johnn ...
isotoxal star ☆ without self-intersecting edges. Generally, star polytopes that are regular only exist in dimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), lin ...
s 2 ⩽ < 5.
In graph theory
In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are conne ...
, all graphs
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discre ...
with 4 or fewer vertices are planar
Planar is an adjective meaning "relating to a plane (geometry)".
Planar may also refer to:
Science and technology
* Planar (computer graphics), computer graphics pixel information from several bitplanes
* Planar (transmission line technologies), ...
, however, there is a graph with 5 vertices that is not: ''K''5, the complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is c ...
with 5 vertices, where every pair of distinct vertices in a pentagon is joined by unique edges belonging to a pentagram. By Kuratowski's theorem
In graph theory, Kuratowski's theorem is a mathematical forbidden graph characterization of planar graphs, named after Kazimierz Kuratowski. It states that a finite graph is planar if and only if it does not contain a subgraph that is a subdi ...
, a finite graph is planar iff
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is bicon ...
it does not contain a subgraph that is a subdivision of ''K''5, or the complete bipartite utility graph
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosopher ...
''K''3,3. A similar graph is the Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is n ...
, which is strongly connected
In the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of an arbitrary directed graph form a partition into subgraphs that ...
and also nonplanar. It is most easily described as graph of a pentagram ''embedded'' inside a pentagon, with a total of 5 crossings
Crossings may refer to:
* ''Crossings'' (Buffy novel), a 2002 original novel based on the U.S. television series ''Buffy the Vampire Slayer''
* Crossings (game), a two-player abstract strategy board game invented by Robert Abbott
* ''Crossings'' ...
, a girth
Girth may refer to:
;Mathematics
* Girth (functional analysis), the length of the shortest centrally symmetric simple closed curve on the unit sphere of a Banach space
* Girth (geometry), the perimeter of a parallel projection of a shape
* Girth ...
of 5, and a Thue number
In the mathematical area of graph theory, the Thue number of a graph is a variation of the chromatic index, defined by and named after mathematician Axel Thue, who studied the squarefree words used to define this number.
Alon et al. define a ''no ...
of 5. The Petersen graph, which is also a distance-regular graph
In the mathematical field of graph theory, a distance-regular graph is a regular graph such that for any two vertices and , the number of vertices at distance from and at distance from depends only upon , , and the distance between and .
...
, is one of only 5 known connected
Connected may refer to:
Film and television
* ''Connected'' (2008 film), a Hong Kong remake of the American movie ''Cellular''
* '' Connected: An Autoblogography About Love, Death & Technology'', a 2011 documentary film
* ''Connected'' (2015 TV ...
vertex-transitive
In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in ...
graphs with no Hamiltonian cycle
In the mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle that visits each vertex ...
s.Royle, G"Cubic Symmetric Graphs (The Foster Census)."
The
automorphism group
In mathematics, the automorphism group of an object ''X'' is the group consisting of automorphisms of ''X'' under composition of morphisms. For example, if ''X'' is a finite-dimensional vector space, then the automorphism group of ''X'' is the g ...
of the Petersen graph is the symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group \m ...
of order 120 = 5!.
The chromatic number
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices o ...
of the plane is at least five, depending on the choice of set-theoretical axioms: the minimum number of colors
Color (American English) or colour (British English) is the visual perceptual property deriving from the spectrum of light interacting with the photoreceptor cells of the eyes. Color categories and physical specifications of color are associa ...
required to color the plane such that no pair of points at a distance of 1 has the same color. Whereas the hexagonal Golomb graph
In graph theory, the Golomb graph is a polyhedral graph with 10 vertices and 18 edges. It is named after Solomon W. Golomb, who constructed it (with a non-planar embedding) as a unit distance graph that requires four colors in any graph colori ...
and the regular hexagonal tiling
In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of or (as a truncated triangular tiling).
English mathemat ...
generate chromatic numbers of 4 and 7, respectively, a chromatic coloring of 5 can be attained under a more complicated graph where multiple four-coloring Moser spindle
In graph theory, a branch of mathematics, the Moser spindle (also called the Mosers' spindle or Moser graph) is an undirected graph, named after mathematicians Leo Moser and his brother William, with seven vertices and eleven edges. It is a unit d ...
s are linked so that no monochromatic triples exist in any coloring of the overall graph, as that would generate an equilateral arrangement that tends toward a purely hexagonal structure
A structure is an arrangement and organization of interrelated elements in a material object or system, or the object or system so organized. Material structures include man-made objects such as buildings and machines and natural objects such as ...
.
The plane
Plane(s) most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
Plane or planes may also refer to:
Biology
* Plane (tree) or ''Platanus'', wetland native plant
* ''Planes' ...
contains a total of five Bravais lattice
In geometry and crystallography, a Bravais lattice, named after , is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
: \mathbf = n_1 \mathbf_1 + n_2 \mathbf_2 + n_ ...
s, or arrays of points defined by discrete translation
Translation is the communication of the Meaning (linguistic), meaning of a #Source and target languages, source-language text by means of an Dynamic and formal equivalence, equivalent #Source and target languages, target-language text. The ...
operations: hexagonal
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A '' regular hexagon'' has ...
, oblique
Oblique may refer to:
* an alternative name for the character usually called a slash (punctuation) ( / )
* Oblique angle, in geometry
*Oblique triangle, in geometry
*Oblique lattice, in geometry
* Oblique leaf base, a characteristic shape of the b ...
, rectangular
In Euclidean geometry, Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a par ...
, centered rectangular, and square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
lattices. The plane can also be tiled monohedrally with convex pentagons
In geometry, a pentagon (from the Greek language, Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple polygon, simple pentagon is ...
in fifteen different ways, three of which have Laves tiling
This table shows the 11 convex uniform tilings (regular and semiregular) of the Euclidean plane, and their dual tilings.
There are three regular and eight semiregular tilings in the plane. The semiregular tilings form new tilings from their dua ...
s as special cases.
Five points are needed to determine a conic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a specia ...
, in the same way that two points are needed to determine a line. A Veronese surface In mathematics, the Veronese surface is an algebraic surface in five-dimensional projective space, and is realized by the Veronese embedding, the embedding of the projective plane given by the complete linear system of conics. It is named after Giu ...
in the projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that do ...
of a conic generalizes a linear
Linearity is the property of a mathematical relationship (''function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear r ...
condition for a point to be contained inside a conic.
 There are
There are Platonic solids
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges c ...
in three-dimensional space
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position (geometry), position of an element (i.e., Point (m ...
: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron. The dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagon ...
in particular contains pentagonal
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
faces, while the icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrica ...
, its dual polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. ...
, has a vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
that is a regular pentagon. There are also :
☆ Regular polyhedron compounds: the stella octangula
The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depict ...
, compound of five tetrahedra, compound of five cubes, compound of five octahedra, and compound of ten tetrahedra. Icosahedral symmetry
In mathematics, and especially in geometry, an object has icosahedral symmetry if it has the same symmetries as a regular icosahedron. Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron (the dual of the ...
is isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
to the alternating group
In mathematics, an alternating group is the group of even permutations of a finite set. The alternating group on a set of elements is called the alternating group of degree , or the alternating group on letters and denoted by or
Basic prop ...
on 5 letters of order 120, realized by actions on these uniform polyhedron compounds.
☆ Space-filling convex polyhedra
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the wo ...
: the triangular prism, hexagonal prism
In geometry, the hexagonal prism is a prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 faces, 18 edges, and 12 vertices..
Since it has 8 faces, it is an octahedron. However, the term ''octahedron'' is primarily used to ...
, cube, truncated octahedron, and gyrobifastigium
In geometry, the gyrobifastigium is the 26th Johnson solid (). It can be constructed by joining two face-regular triangular prisms along corresponding square faces, giving a quarter-turn to one prism. It is the only Johnson solid that can tile ...
. While the cube is the only Platonic solid that can tessellate space on its own, the truncated octahedron and the gyrobifastigium are the only Archimedean and Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that isohedral, each face must be the same polygon, or that the same polygons join around each Vertex (geometry), ver ...
s, respectively, that can also tessellate space with their own copies.
☆ Cell-transitive
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its Face (geometry), faces are the same. More specifically, all faces must be not ...
parallelohedra: any parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidea ...
, as well as the rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.
Properties
The rhombic dodecahedro ...
and elongated dodecahedron
In geometry, the elongated dodecahedron, extended rhombic dodecahedron, rhombo-hexagonal dodecahedron or hexarhombic dodecahedron is a convex dodecahedron with 8 rhombic and 4 hexagonal faces. The hexagons can be made equilateral, or regular de ...
, and the hexagonal prism and truncated octahedron. The cube is a special case of a parallelepiped, with the rhombic dodecahedron the only Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. There are 13 Catalan solids. They are named for the Belgian mathematician Eugène Catalan, who first described them in 1865.
The Catalan sol ...
to tessellate space on its own.
☆ Regular abstract polyhedra, which include the excavated dodecahedron
In geometry, the excavated dodecahedron is a star polyhedron that looks like a dodecahedron with concave pentagonal pyramids in place of its faces. Its exterior surface represents the Ef1g1 stellation of the icosahedron. It appears in Magnus We ...
and the dodecadodecahedron
In geometry, the dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U36. It is the rectification of the great dodecahedron (and that of its dual, the small stellated dodecahedron). It was discovered independently by , and .
The e ...
. They have combinatorial symmetries transitive on flags
A flag is a piece of textile, fabric (most often rectangular or quadrilateral) with a distinctive design and colours. It is used as a symbol, a signalling device, or for decoration. The term ''flag'' is also used to refer to the graphic desi ...
of their elements, with topologies
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ho ...
equivalent to that of toroid
In mathematics, a toroid is a surface of revolution with a hole in the middle. The axis of revolution passes through the hole and so does not intersect the surface. For example, when a rectangle is rotated around an axis parallel to one of its ...
s and the ability to tile the hyperbolic plane
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai– Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P'' ...
.
The 5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It i ...
, or pentatope, is the self-dual fourth-dimensional analogue of the tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
, with Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean refl ...
symmetry of order 120 = 5 ! and group structure. Made of five tetrahedra, its Petrie polygon
In geometry, a Petrie polygon for a regular polytope of dimensions is a skew polygon in which every consecutive sides (but no ) belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a reg ...
is a regular pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
and its orthographic projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Two-dimensional space, two dimensions. Orthographic projection is a form of parallel projection in ...
is equivalent to the complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is c ...
''K''5. It is one of six regular 4-polytopes, made of thirty-one elements: five vertices, ten edges, ten faces
The face is the front of an animal's head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affe ...
, five tetrahedral cells and one 4-face
In solid geometry, a face is a flat surface (a planar region) that forms part of the boundary of a solid object; a three-dimensional solid bounded exclusively by faces is a ''polyhedron''.
In more technical treatments of the geometry of polyhedra ...
.
*A regular 120-cell, the dual ''polychoron'' to the regular 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from " ...
, can fit one hundred and twenty 5-cells. Also, five 24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, oct ...
s fit inside a small stellated 120-cell
In geometry, the small stellated 120-cell or stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
Related polytopes
It has the same edge arrangement as the great gr ...
, the first stellation
In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in ''n'' dimensions to form a new figure. Starting with an original figure, the process extends specific el ...
of the 120-cell.
*A subset of the vertices of the small stellated 120-cell are matched by the great duoantiprism star, which is the only uniform
A uniform is a variety of clothing worn by members of an organization while participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency services, se ...
nonconvex ''duoantiprismatic'' solution in the fourth dimension, constructed from the polytope
In elementary geometry, a polytope is a geometric object with flat sides (''faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -d ...
cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''×''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is
: A\ti ...
and made of fifty tetrahedra
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the o ...
, ten pentagrammic crossed antiprism
In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.
It differs from the pentagrammic antiprism by having oppo ...
s, ten pentagonal antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for ...
s, and fifty vertices.
*The grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope (4-dimensional uniform polytope) bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polytope ...
, which is the only known non-Wythoffian construction of a uniform polychoron, is made of twenty pentagonal antiprisms and three hundred tetrahedra, with a total of one hundred vertices and five hundred edges.
*The abstract four-dimensional 57-cell is made of fifty-seven hemi-icosahedral cells, in-which five surround each edge. The 11-cell
In mathematics, the 11-cell (or hendecachoron) is a self-dual abstract regular 4-polytope ( four-dimensional polytope). Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. It has Schläfli symbol , with 3 hemi-icosahedr ...
, another abstract 4-polytope with eleven vertices and fifty-five edges, is made of eleven hemi-dodecahedral cells each with fifteen dodecahedra. The skeleton
A skeleton is the structural frame that supports the body of an animal. There are several types of skeletons, including the exoskeleton, which is the stable outer shell of an organism, the endoskeleton, which forms the support structure inside ...
of the hemi-dodecahedron is the Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is n ...
.
Overall, the fourth dimension contains five Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group (named after Hermann Weyl) of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections th ...
s that form a finite number of uniform polychora: , , , , and , with four of these Coxeter groups capable of generating the same finite forms without ; accompanied by a fifth or sixth general group of unique 4-prisms of Platonic and Archimedean solids. There are also a total of five Coxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean refl ...
s that generate non-prismatic Eucledian honeycombs in 4-space, alongside five compact hyperbolic Coxeter groups that generate five regular compact hyperbolic honeycombs with finite facets
A facet is a flat surface of a geometric shape, e.g., of a cut gemstone.
Facet may also refer to:
Arts, entertainment, and media
* ''Facets'' (album), an album by Jim Croce
* ''Facets'', a 1980 album by jazz pianist Monty Alexander and his tri ...
, as with the order-5 5-cell honeycomb
In the geometry of hyperbolic 4-space, the order-5 5-cell honeycomb is one of five compact regular space-filling tessellations (or honeycombs). With Schläfli symbol , it has five 5-cells around each face. Its dual is the 120-cell honeycomb, . ...
and the order-5 120-cell honeycomb
In the geometry of hyperbolic 4-space, the order-5 120-cell honeycomb is one of five compact regular space-filling tessellations (or honeycombs). With Schläfli symbol , it has five 120-cells around each face. It is self- dual. It also has 600 1 ...
, both of which have five cells around each face. Compact hyperbolic honeycombs only exist through the fourth dimension, or rank 5, with paracompact hyperbolic solutions existing through rank 10. Likewise, analogues of three-dimensional icosahedral symmetry
In mathematics, and especially in geometry, an object has icosahedral symmetry if it has the same symmetries as a regular icosahedron. Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron (the dual of the ...
or four-dimensional symmetry do not exist in dimensions ''n'' ⩾ 5; however, there is the uniform
A uniform is a variety of clothing worn by members of an organization while participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency services, se ...
prismatic group × in the fifth dimension which contains prisms of regular and uniform 4-polytopes that have symmetry.
The 5-simplex
In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos−1(), or approximately 78.46°.
The 5-s ...
is the five-dimensional
A five-dimensional space is a space with five dimensions. In mathematics, a sequence of ''N'' numbers can represent a location in an ''N''-dimensional space. If interpreted physically, that is one more than the usual three spatial dimensions a ...
analogue of the 5-cell, or 4-simplex; the fifth iteration of -simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
es in any dimensions. The 5-simplex has the Coxeter group as its symmetry group, of order 720 = 6 !, whose group structure is represented by the symmetric group , the only finite symmetric group which has an outer automorphism In mathematics, the outer automorphism group of a group, , is the quotient, , where is the automorphism group of and ) is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted . If is trivial and has a t ...
. The 5-cube
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
It is represented by Schläfli symbol or , constructed as 3 tesseracts, ...
, made of ten tesseract
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eig ...
s and the 5-cell as its vertex figure, is also regular and one of thirty-one uniform 5-polytope
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope Facet (geometry), facets.
The complete set of convex uniform 5-polytopes ...
s under the Coxeter hypercubic group. The demipenteract
In five-dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a ''5-hypercube'' (penteract) with alternated vertices removed.
It was discovered by Thorold Gosset. Since it was the only semiregular 5- ...
, with one hundred and twenty cells, is the only fifth-dimensional semiregular polytope
In geometry, by Thorold Gosset's definition a semiregular polytope is usually taken to be a polytope that is vertex-transitive and has all its facets being regular polytopes. E.L. Elte compiled a longer list in 1912 as ''The Semiregular Polyt ...
, and has the rectified 5-cell
In four-dimensional geometry, the rectified 5-cell is a uniform 4-polytope composed of 5 regular tetrahedral and 5 regular octahedral cells. Each edge has one tetrahedron and two octahedra. Each vertex has two tetrahedra and three octahedra. In t ...
as its vertex figure, which is one of only three semiregular 4-polytopes alongside the rectified 600-cell
In geometry, the rectified 600-cell or rectified hexacosichoron is a convex uniform 4-polytope composed of 600 regular octahedra and 120 icosahedra cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two ico ...
and the snub 24-cell
In geometry, the snub 24-cell or snub disicositetrachoron is a convex uniform 4-polytope composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular face ...
. In the fifth dimension, there are five regular paracompact honeycombs, all with infinite
Infinite may refer to:
Mathematics
*Infinite set, a set that is not a finite set
*Infinity, an abstract concept describing something without any limit
Music
* Infinite (group), a South Korean boy band
*''Infinite'' (EP), debut EP of American m ...
facets
A facet is a flat surface of a geometric shape, e.g., of a cut gemstone.
Facet may also refer to:
Arts, entertainment, and media
* ''Facets'' (album), an album by Jim Croce
* ''Facets'', a 1980 album by jazz pianist Monty Alexander and his tri ...
and vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
s. There are exclusively twelve complex aperiotopes in complex spaces of dimensions ⩾ , with fifteen in and sixteen in ; alongside complex polytopes in and higher under simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
, hypercubic and orthoplex
In geometry, a cross-polytope, hyperoctahedron, orthoplex, or cocube is a regular, convex polytope that exists in ''n''- dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahed ...
groups, the latter with van Oss polytopes.
There are five exceptional Lie groups
In mathematics, a simple Lie group is a connected non-abelian Lie group ''G'' which does not have nontrivial connected normal subgroups. The list of simple Lie groups can be used to read off the list of simple Lie algebras and Riemannian symm ...
: , , , , and . The smallest of these, , can be represented in five-dimensional complex space and projected
Projected is an American rock supergroup consisting of Sevendust members John Connolly and Vinnie Hornsby, Alter Bridge and Creed drummer Scott Phillips, and former Submersed and current Tremonti guitarist Eric Friedman. The band released thei ...
in the same number of dimensions as a ball
A ball is a round object (usually spherical, but can sometimes be ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used f ...
rolling on top of another ball, whose motion
In physics, motion is the phenomenon in which an object changes its position with respect to time. Motion is mathematically described in terms of displacement, distance, velocity, acceleration, speed and frame of reference to an observer and mea ...
is described in two-dimensional space. , the largest of all five exceptional groups, also contains the other four as subgroup
In group theory, a branch of mathematics, given a group ''G'' under a binary operation ∗, a subset ''H'' of ''G'' is called a subgroup of ''G'' if ''H'' also forms a group under the operation ∗. More precisely, ''H'' is a subgroup ...
s and is constructed with one hundred and twenty quaternionic unit icosians that make up the vertices of the 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from " ...
. There are also five solvable group
In mathematics, more specifically in the field of group theory, a solvable group or soluble group is a group that can be constructed from abelian groups using extensions. Equivalently, a solvable group is a group whose derived series terminates ...
s that are excluded from finite simple group
Finite is the opposite of infinite. It may refer to:
* Finite number (disambiguation)
* Finite set, a set whose cardinality (number of elements) is some natural number
* Finite verb, a verb form that has a subject, usually being inflected or marked ...
s of Lie type.
The five Mathieu groups
In group theory, a topic in abstract algebra, the Mathieu groups are the five sporadic simple groups ''M''11, ''M''12, ''M''22, ''M''23 and ''M''24 introduced by . They are multiply transitive permutation groups on 11, 12, 22, 23 or 24 object ...
constitute the first generation in the happy family of sporadic groups
In mathematics, a sporadic group is one of the 26 exceptional groups found in the classification of finite simple groups.
A simple group is a group ''G'' that does not have any normal subgroups except for the trivial group and ''G'' itself. Th ...
. These are also the first five sporadic groups to have been described, defined as multiply transitive permutation groups on objects
Object may refer to:
General meanings
* Object (philosophy), a thing, being, or concept
** Object (abstract), an object which does not exist at any particular time or place
** Physical object, an identifiable collection of matter
* Goal, an ...
, with ∈
In mathematics, an element (or member) of a Set (mathematics), set is any one of the Equality (mathematics), distinct Mathematical object, objects that belong to that set.
Sets
Writing A = \ means that the elements of the set are the numbers 1, ...
. In particular, , the smallest of all sporadic groups, has a rank 3 action
Rank is the relative position, value, worth, complexity, power, importance, authority, level, etc. of a person or object within a ranking, such as:
Level or position in a hierarchical organization
* Academic rank
* Diplomatic rank
* Hierarchy
* ...
on fifty-five points from an induced action on unordered pair In mathematics, an unordered pair or pair set is a set of the form , i.e. a set having two elements ''a'' and ''b'' with no particular relation between them, where = . In contrast, an ordered pair (''a'', ''b'') has ''a'' as its first ...
s, as well as two five-dimensional
A five-dimensional space is a space with five dimensions. In mathematics, a sequence of ''N'' numbers can represent a location in an ''N''-dimensional space. If interpreted physically, that is one more than the usual three spatial dimensions a ...
faithful complex irreducible representations over the field
Field may refer to:
Expanses of open ground
* Field (agriculture), an area of land used for agricultural purposes
* Airfield, an aerodrome that lacks the infrastructure of an airport
* Battlefield
* Lawn, an area of mowed grass
* Meadow, a grass ...
with three elements, which is the lowest irreducible dimensional representation of all sporadic group over their respective fields with ''n'' elements. Of precisely five different conjugacy class
In mathematics, especially group theory, two elements a and b of a group are conjugate if there is an element g in the group such that b = gag^. This is an equivalence relation whose equivalence classes are called conjugacy classes. In other wor ...
es of maximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.
In group theory, a maximal subgroup ''H'' of a group ''G'' is a proper subgroup, such that no proper subgroup ''K'' contains ''H'' s ...
s of , one is the almost simple symmetric group (of order 5 !), and another is , also almost simple, that functions as a point stabilizer which has as its largest prime factor
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
in its group order
In mathematics, the order of a finite group is the number of its elements. If a group (mathematics), group is not finite, one says that its order is ''infinite''. The ''order'' of an element of a group (also called period length or period) is t ...
: 24·32·5 = 2·3·4·5·6 = 8·9·10 = 720. On the other hand, whereas is sharply 4-transitive, is sharply 5-transitive and is 5-transitive, and as such they are the only two 5-transitive groups that are not symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group \m ...
s or alternating group
In mathematics, an alternating group is the group of even permutations of a finite set. The alternating group on a set of elements is called the alternating group of degree , or the alternating group on letters and denoted by or
Basic prop ...
s. has the first five prime numbers as its distinct prime factors in its order of 27· 32·5· 7· 11, and is the smallest of five sporadic groups with five distinct prime factors in their order. All Mathieu groups are subgroups of , which under the Witt design
250px, thumbnail, The Fano plane is a Steiner triple system S(2,3,7). The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line.
In combinatorial mathematics, a Steiner system (named after Jakob Steiner) ...
of Steiner system
250px, thumbnail, The Fano plane is a Steiner triple system S(2,3,7). The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line.
In combinatorial mathematics, a Steiner system (named after Jakob Steiner) ...
S(5, 8, 24) emerges a construction of the extended binary Golay code that has as its automorphism group
In mathematics, the automorphism group of an object ''X'' is the group consisting of automorphisms of ''X'' under composition of morphisms. For example, if ''X'' is a finite-dimensional vector space, then the automorphism group of ''X'' is the g ...
. generates ''octads'' from code words
''Code Words'' is an Electronic publishing, online publication about computer programming produced by the Recurse Center retreat community. It began publishing in December 2014, and has a quarterly schedule.
The journal features original work by p ...
of Hamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string o ...
8 from the extended binary Golay code, one of five different Hamming weights the extended binary Golay code uses: 0, 8, 12, 16, and 24. The Witt design and the extended binary Golay code in turn can be used to generate a faithful construction of the 24-dimensional Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space, which is one of the best models for the kissing number problem. It was discovered by . It may also have been discovered (but not published) by E ...
Λ24, which is the subject of the second generation of seven sporadic groups that are subquotient In the mathematical fields of category theory and abstract algebra, a subquotient is a quotient object of a subobject. Subquotients are particularly important in abelian categories, and in group theory, where they are also known as sections, thou ...
s of the automorphism of the Leech lattice, Conway group .
There are five non-supersingular primes: 37, 43, 53, 61, and 67, all smaller than the largest of fifteen supersingular prime divisor
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
s of the friendly giant, 71.
List of basic calculations
In decimal
5 is the only prime number to end in the digit 5 indecimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral ...
because all other numbers written with a 5 in the ones place are multiples of five, which makes it a 1-automorphic number
In mathematics, an automorphic number (sometimes referred to as a circular number) is a natural number in a given number base b whose square "ends" in the same digits as the number itself.
Definition and properties
Given a number base b, a natura ...
.
All multiples of 5 will end in either 5 or , and vulgar fractions
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
with 5 or in the denominator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
do not yield infinite decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral ...
expansions because they are prime factors of 10, the base.
In the powers of 5, every power ends with the number five, and from 53 onward, if the exponent is odd
Odd means unpaired, occasional, strange or unusual, or a person who is viewed as eccentric.
Odd may also refer to:
Acronym
* ODD (Text Encoding Initiative) ("One Document Does it all"), an abstracted literate-programming format for describing X ...
, then the hundreds digit is 1, and if it is even, the hundreds digit is 6.
A number raised to the fifth power always ends in the same digit as .
Evolution of the Arabic digit

Indian system
In the game of chess, Indian Defence or Indian Game is a broad term for a group of openings characterised by the moves:
:1. d4 Nf6
They are all to varying degrees hypermodern defences, where Black invites White to establish an imposing presenc ...
, as for the digits 1 to 4. The Kushana and Gupta
Gupta () is a common surname or last name of Indian origin. It is based on the Sanskrit word गोप्तृ ''goptṛ'', which means 'guardian' or 'protector'. According to historian R. C. Majumdar, the surname ''Gupta'' was adopted by se ...
empires in what is now India
India, officially the Republic of India (Hindi: ), is a country in South Asia. It is the seventh-largest country by area, the second-most populous country, and the most populous democracy in the world. Bounded by the Indian Ocean on the so ...
had among themselves several different forms that bear no resemblance to the modern digit. The Nagari and Punjabi took these digits and all came up with forms that were similar to a lowercase "h" rotated 180°. The Ghubar Arabs transformed the digit in several different ways, producing from that were more similar to the digits 4 or 3 than to 5. It was from those digits that Europeans finally came up with the modern 5.
While the shape of the character for the digit 5 has an ascender in most modern typeface
A typeface (or font family) is the design of lettering that can include variations in size, weight (e.g. bold), slope (e.g. italic), width (e.g. condensed), and so on. Each of these variations of the typeface is a font.
There are list of type ...
s, in typefaces with text figures
Text figures (also known as non-lining, lowercase, old style, ranging, hanging, medieval, billing, or antique figures or numerals) are numerals designed with varying heights in a fashion that resembles a typical line of running text, hence the ...
the glyph usually has a descender
In typography and handwriting, a descender is the portion of a letter that extends below the baseline of a font.
For example, in the letter ''y'', the descender is the "tail", or that portion of the diagonal line which lies below the ''v'' c ...
, as, for example, in .
On the seven-segment display
A seven-segment display is a form of electronic display device for displaying decimal numerals that is an alternative to the more complex dot matrix displays.
Seven-segment displays are widely used in digital clocks, electronic meters, basic ...
of a calculator, it is represented by five segments at four successive turns from top to bottom, rotating counterclockwise first, then clockwise, and vice-versa.
Science
*Theatomic number
The atomic number or nuclear charge number (symbol ''Z'') of a chemical element is the charge number of an atomic nucleus. For ordinary nuclei, this is equal to the proton number (''n''p) or the number of protons found in the nucleus of every ...
of boron
Boron is a chemical element with the symbol B and atomic number 5. In its crystalline form it is a brittle, dark, lustrous metalloid; in its amorphous form it is a brown powder. As the lightest element of the ''boron group'' it has th ...
.
*The number of appendages on most starfish
Starfish or sea stars are star-shaped echinoderms belonging to the class Asteroidea (). Common usage frequently finds these names being also applied to ophiuroids, which are correctly referred to as brittle stars or basket stars. Starfish ...
, which exhibit pentamerism
Symmetry in biology refers to the symmetry observed in organisms, including plants, animals, fungi, and bacteria. External symmetry can be easily seen by just looking at an organism. For example, take the face of a human being which has a pla ...
.
*The most destructive known hurricanes
A tropical cyclone is a rapidly rotating storm system characterized by a low-pressure center, a closed low-level atmospheric circulation, strong winds, and a spiral arrangement of thunderstorms that produce heavy rain and squalls. Depend ...
rate as Category 5 on the Saffir–Simpson hurricane wind scale.
*The most destructive known tornado
A tornado is a violently rotating column of air that is in contact with both the surface of the Earth and a cumulonimbus cloud or, in rare cases, the base of a cumulus cloud. It is often referred to as a twister, whirlwind or cyclone, altho ...
es rate an F-5 on the Fujita scale
The Fujita scale (F-Scale; ), or Fujita–Pearson scale (FPP scale), is a scale for rating tornado intensity, based primarily on the damage tornadoes inflict on human-built structures and vegetation. The official Fujita scale category is determ ...
or EF-5 on the Enhanced Fujita scale
The Enhanced Fujita scale (abbreviated as EF-Scale) rates tornado intensity based on the severity of the damage they cause. It is used in some countries, including the United States, Canada, China, and Mongolia.
The Enhanced Fujita scale repla ...
.
Astronomy
*Messier object
The Messier objects are a set of 110 astronomical objects catalogued by the French astronomer Charles Messier in his ''Catalogue des Nébuleuses et des Amas d'Étoiles'' (''Catalogue of Nebulae and Star Clusters'').
Because Messier was only int ...
M5, a magnitude 7.0 globular cluster
A globular cluster is a spheroidal conglomeration of stars. Globular clusters are bound together by gravity, with a higher concentration of stars towards their centers. They can contain anywhere from tens of thousands to many millions of membe ...
in the constellation Serpens
Serpens ( grc, , , the Serpent) is a constellation in the northern celestial hemisphere. One of the 48 constellations listed by the 2nd-century astronomer Ptolemy, it remains one of the 88 modern constellations designated by the International ...
.
*The New General Catalogue
The ''New General Catalogue of Nebulae and Clusters of Stars'' (abbreviated NGC) is an astronomical catalogue of deep-sky objects compiled by John Louis Emil Dreyer in 1888. The NGC contains 7,840 objects, including galaxies, star clusters and ...
br>objectNGC 5
NGC commonly refers to:
* New General Catalogue of Nebulae and Clusters of Stars, a catalogue of deep sky objects in astronomy
NGC may also refer to:
Companies
* NGC Corporation, name of US electric company Dynegy, Inc. from 1995 to 1998
* Nati ...
, a magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
13 spiral galaxy
Spiral galaxies form a class of galaxy originally described by Edwin Hubble in his 1936 work ''The Realm of the Nebulae''constellation
A constellation is an area on the celestial sphere in which a group of visible stars forms Asterism (astronomy), a perceived pattern or outline, typically representing an animal, mythological subject, or inanimate object.
The origins of the e ...
Andromeda.
*The Roman numeral V stands for dwarfs (main sequence
In astronomy, the main sequence is a continuous and distinctive band of stars that appears on plots of stellar color versus brightness. These color-magnitude plots are known as Hertzsprung–Russell diagrams after their co-developers, Ejnar Her ...
stars) in the Yerkes spectral classification scheme
In astronomy, stellar classification is the classification of stars based on their stellar spectrum, spectral characteristics. Electromagnetic radiation from the star is analyzed by splitting it with a Prism (optics), prism or diffraction grati ...
.
*The Roman numeral V (usually) stands for the fifth-discovered satellite of a planet or minor planet (e.g. Jupiter V).
*There are five Lagrangian point
In celestial mechanics, the Lagrange points (; also Lagrangian points or libration points) are points of equilibrium for small-mass objects under the influence of two massive orbiting bodies. Mathematically, this involves the solution of th ...
s in a two-body system.
Biology
*There are generally considered to be five senses. *The five basictaste
The gustatory system or sense of taste is the sensory system that is partially responsible for the perception of taste (flavor). Taste is the perception produced or stimulated when a substance in the mouth reacts chemically with taste receptor ...
s are sweetness, sweet, taste#Saltiness, salty, taste#Sourness, sour, taste#Bitterness, bitter, and umami.
*Almost all amphibians, reptiles, and mammals which have fingers or toes have five of them on each extremity.
Computing
*5 is the ASCII code of the Enquiry character, which is abbreviated to ENQ.Religion and culture
Hinduism
*The god Shiva has five faces and his mantra is also called (five-worded) mantra. *The goddess Saraswati, goddess of knowledge and intellectual is associated with or the number 5. *There are Pancha Bhoota, five elements in the universe according to Hindu cosmology: (earth, fire, water, air and space respectively). *The most sacred tree in Hinduism has 5 leaves in every leaf stunt. *Most of the flowers have 5 petals in them. *The epic Mahabharata revolves around the battle between Duryodhana and his 99 other brothers and the 5 pandava princes—Yudhisthira, Dharma, Arjuna, Bhima, Nakula and Sahadeva.Christianity
*There are traditionally Five Wounds, five wounds of Jesus Christ in Christianity: the Flagellation of Christ, Scourging at the Pillar, Crown of Thorns, the Crowning with Thorns, the wounds in Christ's hands, the wounds in Christ's feet, and the Holy Lance, Side Wound of Christ.Gnosticism
*The number five was an important symbolic number in Manichaeism, with heavenly beings, concepts, and others often grouped in sets of five. *Five Seals in Sethianism *Five Trees in the Gospel of ThomasIslam
*The Five Pillars of Islam *Muslims pray to Allah five times a day *According to Shia Muslims, the Panjetan-e-Pak, Panjetan or the Five Holy Purified Ones are the members of Muhammad's family: Muhammad, Ali, Fatimah, Hasan ibn Ali, Hasan, and Husayn ibn Ali, Husayn and are often symbolically represented by an image of the Hamsa, Khamsa.Judaism
*The Torah contains five books—Book of Genesis, Genesis, Book of Exodus, Exodus, Book of Leviticus, Leviticus, Book of Numbers, Numbers, and Book of Deuteronomy, Deuteronomy—which are collectively called the Five Books of Moses, the Pentateuch (Greek language, Greek for "five containers", referring to the scroll cases in which the books were kept), or Chumash (Judaism), Humash (, Hebrew language, Hebrew for "fifth"). *The book of Psalms is arranged into five books, paralleling the Five Books of Moses. *The Hamsa, Khamsa, an ancient symbol shaped like a hand with four fingers and one thumb, is used as a protective amulet by Jews; that same symbol is also very popular in Arabic culture, known to protect from envy and the evil eye.Sikhism
*The five sacred Sikh symbols prescribed by Guru Gobind Singh are commonly known as or the "The Five Ks, Five Ks" because they start with letter K representing in the Punjabi language's Gurmukhi script. They are: (unshorn hair), (the comb), (the steel bracelet), (the soldier's shorts), and (the sword) (in Gurmukhi: ). Also, there are five deadly evils: (lust), (anger), (attachment), (greed), and (ego).Daoism
*Wuxing (Chinese philosophy), 5 Elements *Three Sovereigns and Five Emperors, 5 EmperorsOther religions and cultures
*According to ancient Greek philosophers such as Aristotle, the universe is made up of five classical elements: water (classical element), water, earth (classical element), earth, air (classical element), air, fire (classical element), fire, and aether (classical element), ether. This concept was later adopted by medieval alchemists and more recently by practitioners of Neo-Pagan religions such as Wicca. *Thepentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle aroun ...
, or five-pointed star, bears religious significance in various faiths including Baháʼí Faith, Baháʼí, Christianity, Freemasonry, Satanism, Taoism, Thelema, and Wicca.
*In Cantonese, "five" sounds like the word "not" (character: ). When five appears in front of a lucky number, e.g. "58", the result is considered unlucky.
*In East Asian tradition, there are five elements: (water (Wu Xing), water, fire (Wu Xing), fire, earth (Wu Xing), earth, tree (Wu Xing), wood, and metal (Wu Xing), metal). The Japanese language, Japanese names for the week-day names, days of the week, Tuesday through Saturday, come from these elements via the identification of the elements with the Classical planet, five planets visible with the naked eye. Also, the traditional Japanese calendar has a five-day weekly cycle that can be still observed in printed mixed calendars combining Western, Chinese-Buddhist, and Japanese names for each weekday.
*In numerology, 5 or a series of 555 (number), 555, is often associated with change, evolution, love and abundance.
*Members of The Nation of Gods and Earths, a primarily African American religious organization, call themselves the "Five-Percenters" because they believe that only 5% of mankind is truly enlightened.
Art, entertainment, and media
Fictional entities
*James the Red Engine, a fictional character numbered 5. *Johnny 5 is the lead character in the film ''Short Circuit'' (1986) *Number Five is a character in Lorien Legacies *Sankara Stones, five magical rocks in ''Indiana Jones and the Temple of Doom'' that are sought by the Thuggees for evil purposes *The Mach Five , the racing car Speed Racer ( in the Japanese version) drives in the anime series of the same name (known as "Mach Go! Go! Go!" in Japan) *In the works of J. R. R. Tolkien, five wizards (Saruman, Gandalf, Radagast, Blue Wizards, Alatar and Pallando) are sent to Middle-earth to aid against the threat of the Dark Lord Sauron *In the ''A Song of Ice and Fire'' series, the War of the Five Kings is fought between different claimants to the Iron Throne of Westeros, as well as to the thrones of the individual regions of Westeros (Joffrey Baratheon, Stannis Baratheon, Renly Baratheon, Robb Stark and Balon Greyjoy) *In ''The Wheel of Time'' series, the "Emond's Field Five" are a group of five of the series' main characters who all come from the village of Emond's Field (Rand al'Thor, Matrim Cauthon, Perrin Aybara, Egwene al'Vere and Nynaeve al'Meara) *Myst (series), ''Myst'' uses the number 5 as a unique base counting system. In ''The Myst Reader'' series, it is further explained that the number 5 is considered a holy number in the fictional D'ni society. *Number Five is also a character in The Umbrella Academy comic book and TV series adaptationFilms
*Towards the end of the film ''Monty Python and the Holy Grail'' (1975), the character of King Arthur repeatedly confuses the number five with the number 3, three. *''Five Go Mad in Dorset'' (1982) was the first of the long-running series of ''The Comic Strip, The Comic Strip Presents...'' television comedy films *''The Fifth Element'' (1997), a science fiction film * ''Fast Five'' (2011), the fifth installment of the The Fast and the Furious (series), ''Fast and Furious'' film series. *''V for Vendetta (film), V for Vendetta'' (2005), produced by Warner Bros., directed by James McTeigue, and adapted from Alan Moore's graphic novel ''V for Vendetta'' prominently features number 5 and Roman Numeral V; the story is based on the historical event in which a group of men attempted to destroy Parliament on November 5, 1605Music
Groups
*Five (group), a UK Boy band *The Five (composers), 19th-century Russian composers *5 Seconds of Summer, pop band that originated in Sydney, Australia *Five Americans, American rock band active 1965–1969 *Five Finger Death Punch, American heavy metal band from Las Vegas, Nevada. Active 2005–present *Five Man Electrical Band, Canadian rock group billed (and active) as the Five Man Electrical Band, 1969–1975 *Maroon 5, American pop rock band that originated in Los Angeles, California *MC5, American punk rock band *Pentatonix, a Grammy-winning a cappella group originated in Arlington, Texas *The 5th Dimension, American pop vocal group, active 1977–present *The Dave Clark Five, a.k.a. DC5, an English pop rock group comprising Dave Clark (musician), Dave Clark, Lenny Davidson, Rick Huxley, Denis Payton, and Mike Smith (Dave Clark Five), Mike Smith; active 1958–1970 *The Jackson 5, American pop rock group featuring various members of the Jackson family; they were billed (and active) as The Jackson 5, 1966–1975 *Hi-5 (Australian group), Hi-5, Australian pop kids group, where it has several international adaptations, and several members throughout the history of the band. It was also a TV show. *We Five: American folk rock group active 1965–1967 and 1968–1977 *Grandmaster Flash and the Furious Five: American rap group, 1970–80's *Fifth Harmony, an American girl group. *Ben Folds Five, an American alternative rock trio, 1993–2000, 2008 and 2011–2013 *R5 (band), an American pop and alternative rock group, 2009–2018Other uses
*A perfect fifth is the most consonant harmony, and is the basis for most western tuning systems. *Modern musical notation uses a staff (music), musical staff made of five horizontal lines. *In harmonics – the fifth harmonic series (music), partial (or 4th overtone) of a fundamental frequency, fundamental has a frequency ratio of 5:1 to the frequency of that fundamental. This ratio corresponds to the interval of 2 octaves plus a pure major third. Thus, the interval of 5:4 is the interval of the pure third. A major and minor, major Triad (music), triad chord (music), chord when played in just intonation (most often the case in a cappella vocal ensemble singing), will contain such a pure major third. *The number of completed, numbered piano concertos of Ludwig van Beethoven, Sergei Prokofiev, and Camille Saint-Saëns. *Using the Latin root, five musicians are called a quintet. *A scale with five notes per octave is called a pentatonic scale. *Five is the lowest possible number that can be the top number of a time signature with an asymmetric meter (music), meter.Television
;Stations *Channel 5 (UK), a television channel that broadcasts in the United Kingdom *5 (TV channel) (''formerly known as ABC 5 and TV5'') (DWET-TV channel 5 In Metro Manila) a television network in the Philippines. ; ;Series *''Babylon 5'', a science fiction television series *The number 5 features in the television series Battlestar Galactica (2004 TV series), ''Battlestar Galactica'' in regards to the Final Five (Battlestar Galactica), Final Five cylons and the Temple of Five *Hi-5 (Australian TV series), ''Hi-5'' (Australian TV series), a television series from Australia *Hi-5 (UK TV series), ''Hi-5'' (UK TV series), a television show from the United Kingdom *Hi-5 Philippines, ''Hi-5'' Philippines a television show from the Philippines *''Odyssey 5'', a 2002 science fiction television series *''Tillbaka till Vintergatan'', a Swedish children's television series featuring a character named "Femman" (meaning five), who can only utter the word 'five'. *''The Five (talk show), The Five'' The Five (talk show), (talk show): Fox News Channel roundtable current events television show, premiered 2011, so-named for its panel of five commentators. *''Yes! PreCure 5'' is a 2007 anime series which follows the adventures of Nozomi and her friends. It is also followed by the 2008 sequel ''Yes! Pretty Cure 5 GoGo!'' *''The Quintessential Quintuplets'' is a 2019 slice of life romance anime series which follows the everyday life of five identical quintuplets and their interactions with their tutor. It has two seasons, and a final movie is scheduled in summer 2022. *Hawaii Five-0 (2010 TV series), ''Hawaii Five-0'', CBS American TV series.Literature
*The Famous Five (novel series), ''The Famous Five'' is a series of children's books by British writer Enid Blyton *''The Power of Five'' is a series of children's books by British writer and screenwriter Anthony Horowitz *''The Fall of Five'' is a book written under the collective pseudonym Pittacus Lore in the series ''Lorien Legacies'' *''The Book of Five Rings'' is a text on kenjutsu and the martial arts in general, written by the swordsman Miyamoto Musashi circa 1645 *''Slaughterhouse-Five'' is a book by Kurt Vonnegut about World War IISports
*The Olympic Games have five interlocked rings as their symbol, representing the number of inhabited continents represented by the Olympians (Europe, Asia, Africa, Australia and Oceania, and the Americas). * In AFL Women's, the top level of Women's Australian rules football, women's Australian rules football, each team is allowed 5 "Interchange (Australian rules football), interchanges" (substitute players), who can be freely substituted at any time. *In Baseball scorekeeping#Defensive positions, baseball scorekeeping, the number 5 represents the third baseman's position. *In basketball: **The number 5 is used to represent the position of center (basketball), center. **Each team has five players on the court at a given time. Thus, the phrase "five on five" is commonly used to describe standard competitive basketball. **The Five-second rule (basketball), "5-second rule" refers to several related rules designed to promote continuous play. In all cases, violation of the rule results in a turnover. **Under the FIBA (used for all international play, and most non-US leagues) and College basketball, NCAA women's rule sets, a team begins shooting Bonus (basketball), bonus free throws once its opponent has committed five Personal foul (basketball), personal fouls in a quarter. **Under the FIBA rules, A player fouls out and must leave the game after committing five fouls *Five-a-side football is a variation of association football in which each team fields five players. *In ice hockey: ** A major penalty lasts five minutes. ** There are five different ways that a player can score a goal (teams at even strength, team on the power play, team playing shorthanded, penalty shot, and empty net). ** The area between the goaltender's legs is known as the five-hole. *In most rugby league competitions, the starting Rugby league positions#Wing, left wing wears this number. An exception is the Super League, which uses static squad numbering. *In rugby union: ** A Try (rugby), try is worth 5 points. ** One of the two starting Lock (rugby union), lock forwards wears number 5, and usually jumps at number 4 in the line-out (rugby union), line-out. ** In the National Rugby League (France), French variation of the Rugby union bonus points system, bonus points system, a bonus point in the league standings is awarded to a team that loses by 5 or fewer points.Technology
*5 is the most common number of gears for automobiles with manual transmission. *In radio communication, the term "Five by five" is used to indicate perfect signal strength and clarity. *On almost all devices with a numeric keypad such as telephones, computers, etc., the 5 key has a raised dot or raised bar to make dialing easier. Persons who are blind or have low vision find it useful to be able to feel the keys of a telephone. All other numbers can be found with their relative position around the 5 button (on computer keyboards, the 5 key of the numeric keypad, numpad has the raised dot or bar, but the 5 key that shifts with % does not). *On most telephones, the 5 key is associated with the letters J, K, and L, but on some of the BlackBerry phones, it is the key for G and H. *The Pentium, coined by Intel Corporation, is a fifth-generation x86 architecture microprocessor. *The resin identification code used in recycling to identify polypropylene.Miscellaneous fields
Five can refer to: *"Give me five" is a common phrase used preceding a high five. *An informal term for the British Security Service, MI5. *Five babies born at one time are multiple birth, quintuplets. The most famous set of quintuplets were the Dionne quintuplets born in the 1930s. *In the United States legal system, the Fifth Amendment to the United States Constitution can be referred to in court as "pleading the fifth", absolving the defendant from self-incrimination. *Pentameter is verse with five repeating feet per line; iambic pentameter was the most popular form in William Shakespeare, Shakespeare. *Aether (classical element), Quintessence, meaning "fifth element", refers to the elusive fifth element that completes the basic four elements (water, fire, air, and earth) *The designation of an Interstate Highway System, Interstate Highway (Interstate 5) that runs from San Diego, California to Blaine, Washington. In addition, all major north-south Interstate Highways in the United States end in 5. *In the computer game ''Riven'', 5 is considered a holy number, and is a recurring theme throughout the game, appearing in hundreds of places, from the number of islands in the game to the number of bolts on pieces of machinery. *''The Garden of Cyrus'' (1658) by Sir Thomas Browne is a Pythagorean discourse based upon the number 5. *The holy number of Discordianism, as dictated by the Discordianism#Law of Fives, Law of Fives. *The number of Justices on the Supreme Court of the United States necessary to render a majority decision. *The number of dots in a quincunx. *The number of permanent members with veto power on the United Nations Security Council. *The number of sides and the number of angles in a pentagon. *The number of points in apentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle aroun ...
.
*The number of Korotkoff sounds when measuring blood pressure
*The drink Five Alive is named for its five ingredients. The drink Punch (drink), punch derives its name after the Sanskrit पञ्च (pañc) for having five ingredients.
*The Keating Five were five United States Senate, United States Senators accused of corruption in 1989.
*The Inferior Five: Merryman, Awkwardman, The Blimp, White Feather, and Dumb Bunny. DC Comics parody superhero team.
*Chanel No. 5, No. 5 is the name of the iconic fragrance created by Coco Chanel.
*The Committee of Five was delegated to draft the United States United States Declaration of Independence, Declaration of Independence.
*The five-second rule is a commonly used rule of thumb for dropped food.
*555 95472, usually referred to simply as 5, is a minor male character in the comic strip ''Peanuts''.
See also
*Five Families *Five Nations (disambiguation) *555 (number) *List of highways numbered 5References
*Wells, D. ''The Penguin Dictionary of Curious and Interesting Numbers'' London: Penguin Group. (1987): 58–67External links
* *The Number 5
{{DEFAULTSORT:5 (Number) Integers 5 (number)