|
Parallelohedron
In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron. Classification Every parallelohedron is a zonohedron, constructed as the Minkowski sum of between three and six line segments. Each of these line segments can have any positive real number as its length, and each edge of a parallelohedron is parallel to one of these generating segments, with the same length. If the length of a segments of a parallelohedron generated from four or more segments is reduced to zero, the result is that the polyhedron degenerates to a simpler form, a parallelohedron formed from one fewer segment. As a zonohedron, these shap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelohedron Edges Cube
In geometry, a parallelohedron is a polyhedron that can be Translation (geometry), translated without rotations in 3-dimensional Euclidean space to fill space with a Honeycomb (geometry), honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron. Classification Every parallelohedron is a zonohedron, constructed as the Minkowski sum of between three and six line segments. Each of these line segments can have any positive real number as its length, and each edge of a parallelohedron is parallel to one of these generating segments, with the same length. If the length of a segments of a parallelohedron generated from four or more segments is reduced to zero, the result is that the polyhedron Degeneracy (mathematics), degenerates to a simpler form, a para ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
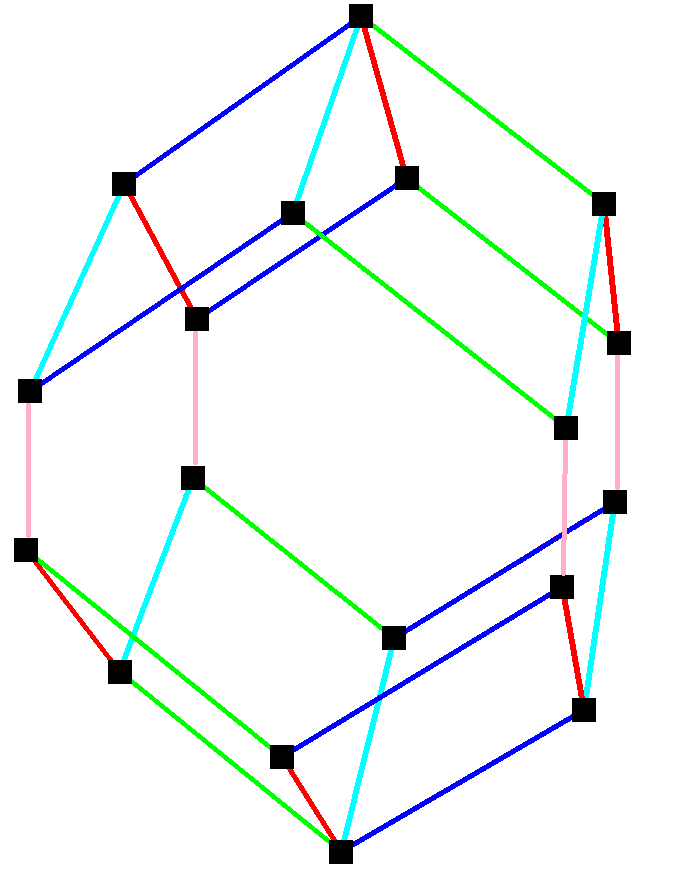
Parallelohedron Edges Elongated Rhombic Dodecahedron
In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron. Classification Every parallelohedron is a zonohedron, constructed as the Minkowski sum of between three and six line segments. Each of these line segments can have any positive real number as its length, and each edge of a parallelohedron is parallel to one of these generating segments, with the same length. If the length of a segments of a parallelohedron generated from four or more segments is reduced to zero, the result is that the polyhedron degenerates to a simpler form, a parallelohedron formed from one fewer segment. As a zonohedron, these shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelohedron Edges Hexagonal Prism
In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron. Classification Every parallelohedron is a zonohedron, constructed as the Minkowski sum of between three and six line segments. Each of these line segments can have any positive real number as its length, and each edge of a parallelohedron is parallel to one of these generating segments, with the same length. If the length of a segments of a parallelohedron generated from four or more segments is reduced to zero, the result is that the polyhedron degenerates to a simpler form, a parallelohedron formed from one fewer segment. As a zonohedron, these shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelohedron Edges Rhombic Dodecahedron
In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron. Classification Every parallelohedron is a zonohedron, constructed as the Minkowski sum of between three and six line segments. Each of these line segments can have any positive real number as its length, and each edge of a parallelohedron is parallel to one of these generating segments, with the same length. If the length of a segments of a parallelohedron generated from four or more segments is reduced to zero, the result is that the polyhedron degenerates to a simpler form, a parallelohedron formed from one fewer segment. As a zonohedron, these shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelohedron Edge Truncated Octahedron
In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron. Classification Every parallelohedron is a zonohedron, constructed as the Minkowski sum of between three and six line segments. Each of these line segments can have any positive real number as its length, and each edge of a parallelohedron is parallel to one of these generating segments, with the same length. If the length of a segments of a parallelohedron generated from four or more segments is reduced to zero, the result is that the polyhedron degenerates to a simpler form, a parallelohedron formed from one fewer segment. As a zonohedron, these shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Honeycomb (geometry)
In geometry, a honeycomb is a ''space filling'' or '' close packing'' of polyhedral or higher-dimensional ''cells'', so that there are no gaps. It is an example of the more general mathematical ''tiling'' or ''tessellation'' in any number of dimensions. Its dimension can be clarified as ''n''-honeycomb for a honeycomb of ''n''-dimensional space. Honeycombs are usually constructed in ordinary Euclidean ("flat") space. They may also be constructed in non-Euclidean spaces, such as hyperbolic honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space. Classification There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered. The simplest honeycombs to build are formed from stacked layers or ''slabs'' of prisms based on some tessellations of the plane. In particu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zonohedron
In geometry, a zonohedron is a convex polyhedron that is centrally symmetric, every face of which is a polygon that is centrally symmetric (a zonogon). Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional projection of a hypercube. Zonohedra were originally defined and studied by E. S. Fedorov, a Russian crystallographer. More generally, in any dimension, the Minkowski sum of line segments forms a polytope known as a zonotope. Zonohedra that tile space The original motivation for studying zonohedra is that the Voronoi diagram of any lattice forms a convex uniform honeycomb in which the cells are zonohedra. Any zonohedron formed in this way can tessellate 3-dimensional space and is called a primary parallelohedron. Each primary parallelohedron is combinatorially equivalent to one of five types: the rhombohedron (including the cube), hexagonal prism, truncated octahedron, rhomb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Dodecahedron
In geometry, the elongated dodecahedron, extended rhombic dodecahedron, rhombo-hexagonal dodecahedron or hexarhombic dodecahedron is a convex dodecahedron with 8 rhombic and 4 hexagonal faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a rhombic dodecahedron elongated by a square prism. Parallelohedron Along with the rhombic dodecahedron, it is a space-filling polyhedron, one of the five types of parallelohedron identified by Evgraf Fedorov that tile space face-to-face by translations. It has 5 sets of parallel edges, called zones or belts. : Tessellation * It can tesselate all space by translations. * It is the Wigner–Seitz cell for certain body-centered tetragonal lattices. This is related to the rhombic dodecahedral honeycomb with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a square tiling with the rhombi projected into squares. Var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron. Properties The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long face-diagonal length is exactly times the short face-diagonal length; thus, the acute angles on each face measure arccos(), or approximately 70.53°. Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on its set of faces. In elementary terms, this means that for any two faces A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic dodecahedron can be viewed as the convex hull of the union of the vertices of a cube and an octahedron. The 6 vertices where 4 rhombi meet corres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron. Properties The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long face-diagonal length is exactly times the short face-diagonal length; thus, the acute angles on each face measure arccos(), or approximately 70.53°. Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on its set of faces. In elementary terms, this means that for any two faces A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic dodecahedron can be viewed as the convex hull of the union of the vertices of a cube and an octahedron. The 6 vertices where 4 rhombi meet corres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Dodecahedron
In geometry, the elongated dodecahedron, extended rhombic dodecahedron, rhombo-hexagonal dodecahedron or hexarhombic dodecahedron is a convex dodecahedron with 8 rhombic and 4 hexagonal faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a rhombic dodecahedron elongated by a square prism. Parallelohedron Along with the rhombic dodecahedron, it is a space-filling polyhedron, one of the five types of parallelohedron identified by Evgraf Fedorov that tile space face-to-face by translations. It has 5 sets of parallel edges, called zones or belts. : Tessellation * It can tesselate all space by translations. * It is the Wigner–Seitz cell for certain body-centered tetragonal lattices. This is related to the rhombic dodecahedral honeycomb with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a square tiling with the rhombi projected into squares. Var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate (or "pack") 3-dimensional space, as a permutohedron. The truncated octahedron was called the "mecon" by Buckminster Fuller. Its dual polyhedron is the tetrakis hexahedron. If the original truncated octahedron has unit edge length, its dual tetrakis hexahedron has edge lengths and . Construction A truncated octahedron is constructed from a regular octahedron with side length 3''a'' by the removal of six right square pyramids, one from each point. These pyramids have both base side length (''a'') and lateral s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |