truncated octahedron

In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagons and 6 squares), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron G_IV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate (or "pack") 3-dimensional space, as a permutohedron.

The truncated octahedron was called the "mecon" by Buckminster Fuller.

Its dual polyhedron is the tetrakis hexahedron. If the original truncated octahedron has unit edge length, its dual tetrakis hexahedron has edge lengths and .

Construction

A truncated octahedron is constructed from a regular octahedron with side length 3''a'' by the removal of six right square pyramids, one from each point. These pyramids have both base side length (''a'') and lateral side length (''e'') of ''a'', to form equilateral triangles. The base area is then ''a''². Note that this shape is exactly similar to half an octahedron or Johnson solid J₁.

From the properties of square pyramids, we can now find the slant height, ''s'', and the height, ''h'', of the pyramid:
:$\begin h &= \sqrt &&= \tfraca \\ s &= \sqrt &&= \sqrt &&= \tfraca \end$

The volume, ''V'', of the pyramid is given by:
:$V = \tfraca^2h = \tfraca^3$

Because six pyramids are removed by truncation, there is a total lost volume of ''a''³.

Orthogonal projections

The truncated octahedron has five special orthogonal projections, centered, on a vertex, on two types of edges, and two types of faces: Hexagon, and square. The last two correspond to the B₂ and A₂ Coxeter planes.

Spherical tiling

The truncated octahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Coordinates

All permutations of (0, ±1, ±2) are Cartesian coordinates of the vertices of a truncated octahedron of edge length a = √2 centered at the origin. The vertices are thus also the corners of 12 rectangles whose long edges are parallel to the coordinate axes.

The edge vectors have Cartesian coordinates and permutations of these. The face normals (normalized cross products of edges that share a common vertex) of the 6 square faces are , and . The face normals of the 8 hexagonal faces are . The dot product between pairs of two face normals is the cosine of the dihedral angle between adjacent faces, either − or −. The dihedral angle is approximately 1.910633 radians (109.471° ) at edges shared by two hexagons or 2.186276 radians (125.263° ) at edges shared by a hexagon and a square.

Dissection

The truncated octahedron can be dissected into a central octahedron, surrounded by 8 triangular cupolae on each face, and 6 square pyramids above the vertices.

Removing the central octahedron and 2 or 4 triangular cupolae creates two Stewart toroids, with dihedral and tetrahedral symmetry:

Permutohedron

The truncated octahedron can also be represented by even more symmetric coordinates in four dimensions: all permutations of (1, 2, 3, 4) form the vertices of a truncated octahedron in the three-dimensional subspace . Therefore, the truncated octahedron is the permutohedron of order 4: each vertex corresponds to a permutation of (1, 2, 3, 4) and each edge represents a single pairwise swap of two elements.

Area and volume

The surface area ''S'' and the volume ''V'' of a truncated octahedron of edge length ''a'' are:
:$\begin S &= \left(6+12\sqrt\right) a^2 &&\approx 26.784\,6097a^2 \\ V &= 8\sqrt a^3 &&\approx 11.313\,7085a^3. \end$

Uniform colorings

There are two uniform colorings, with tetrahedral symmetry and octahedral symmetry, and two 2-uniform coloring with dihedral symmetry as a ''truncated triangular antiprism''. The constructional names are given for each. Their Conway polyhedron notation is given in parentheses.

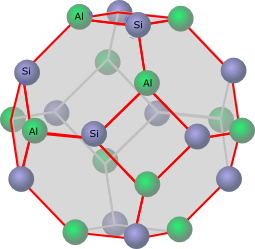
Chemistry

The truncated octahedron exists in the structure of the faujasite crystals.
:

Data hiding

The truncated octahedron (in fact, the generalized truncated octahedron) appears in the error analysis of quantization index modulation (QIM) in conjunction with repetition coding.

Related polyhedra

The truncated octahedron is one of a family of uniform polyhedra related to the cube and regular octahedron.

It also exists as the omnitruncate of the tetrahedron family:

Symmetry mutations

This polyhedron is a member of a sequence of uniform patterns with vertex figure (4.6.2''p'') and Coxeter–Dynkin diagram . For ''p'' < 6, the members of the sequence are omnitruncated polyhedra ( zonohedra), shown below as spherical tilings. For ''p'' > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.

The truncated octahedron is topologically related as a part of sequence of uniform polyhedra and tilings with vertex figures ''n''.6.6, extending into the hyperbolic plane:

The truncated octahedron is topologically related as a part of sequence of uniform polyhedra and tilings with vertex figures 4.2''n''.2''n'', extending into the hyperbolic plane:

Related polytopes

The '' truncated octahedron'' ( bitruncated cube), is first in a sequence of bitruncated hypercubes:

It is possible to slice a tesseract by a hyperplane so that its sliced cross-section is a truncated octahedron.

Tessellations

The truncated octahedron exists in three different convex uniform honeycombs ( space-filling tessellations):

The cell-transitive bitruncated cubic honeycomb can also be seen as the Voronoi tessellation of the body-centered cubic lattice. The truncated octahedron is one of five three-dimensional primary parallelohedra.

Objects

14-sided Chinese dice from warring states period.jpg , ancient Chinese die
CvO 2.jpg , sculpture in Bonn
DaYan Gem solved cubemeister com.jpg , Rubik's Cube variant
Polydron 1170197.jpg , model made with Polydron construction set
Pyrite-249304.jpg , Pyrite crystal

Truncated octahedral graph

In the mathematical field of graph theory, a truncated octahedral graph is the graph of vertices and edges of the truncated octahedron. It has 24 vertices and 36 edges, and is a cubic Archimedean graph. It has book thickness 3 and queue number 2.

As a Hamiltonian cubic graph, it can be represented by LCF notation in multiple ways: , −7, 7, −3sup>6, , −11, 11, 7, 5, −5, −7, −11, 11, −5, −7, 7sup>2, and ��11, 5, −3, −7, −9, 3, −5, 5, −3, 9, 7, 3, −5, 11, −3, 7, 5, −7, −9, 9, 7, −5, −7, 3

References

* (Section 3–9)
*
*
*
*
*
*

External links

*
**
*
*
Editable printable net of a truncated octahedron with interactive 3D view

{{Polyhedron navigator

Uniform polyhedra
Archimedean solids
Space-filling polyhedra
Truncated tilings
Zonohedra