|
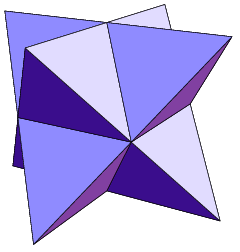
Regular Icosahedron
The regular icosahedron (or simply ''icosahedron'') is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with Regular polygon, regular faces to each of its pentagonal faces, or by putting points onto the cube. The resulting polyhedron has 20 equilateral triangles as its faces, 30 edges, and 12 vertices. It is an example of a Platonic solid and of a deltahedron. The icosahedral graph represents the Skeleton (topology), skeleton of a regular icosahedron. Many polyhedra are constructed from the regular icosahedron. A notable example is the stellation of regular icosahedron, which consists of 59 polyhedrons. The great dodecahedron, one of the Kepler–Poinsot polyhedra, is constructed by either stellation or faceting. Some of the Johnson solids can be constructed by removing the pentagonal pyramids. The regular icosahedron's dual polyhedron is the regular dodecahedron, and their relation has a historical background on the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Deltahedron
A deltahedron is a polyhedron whose faces are all equilateral triangles. The deltahedron was named by Martyn Cundy, after the Greek capital letter delta resembling a triangular shape Δ. Deltahedra can be categorized by the property of convexity. The simplest convex deltahedron is the regular tetrahedron, a pyramid with four equilateral triangles. There are eight convex deltahedra, which can be used in the applications of chemistry as in the polyhedral skeletal electron pair theory and chemical compounds. There are infinitely many concave deltahedra. Strictly convex deltahedron A polyhedron is said to be ''convex'' if a line between any two of its vertices lies either within its interior or on its boundary, and additionally, if no two faces are coplanar (lying in the same plane) and no two edges are collinear (segments of the same line), it can be considered as being strictly convex. Of the eight convex deltahedra, three are Platonic solids and five are Johnson solids. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Skeleton (topology)
In mathematics, particularly in algebraic topology, the of a topological space presented as a simplicial complex (resp. CW complex) refers to the subspace that is the union of the simplices of (resp. cells of ) of dimensions In other words, given an inductive definition of a complex, the is obtained by stopping at the . These subspaces increase with . The is a discrete space, and the a topological graph. The skeletons of a space are used in obstruction theory, to construct spectral sequences by means of filtrations, and generally to make inductive arguments. They are particularly important when has infinite dimension, in the sense that the do not become constant as In geometry In geometry, a of P (functionally represented as skel''k''(''P'')) consists of all elements of dimension up to ''k''. For example: : skel0(cube) = 8 vertices : skel1(cube) = 8 vertices, 12 edges : skel2(cube) = 8 vertices, 12 edges, 6 square faces For simplicial sets The above ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pentagonal Pyramid
In geometry, a pentagonal pyramid is a Pyramid (geometry), pyramid with a pentagon base and five triangular faces, having a total of six faces. It is categorized as a Johnson solid if all of the edges are equal in length, forming Equilateral triangle, equilateral triangular faces and a regular pentagonal base. Pentagonal pyramids occur as pieces and tools in the construction of many polyhedra. They also appear in the field of natural science, as in stereochemistry where the shape can be described as the pentagonal pyramidal molecular geometry, as well as the study of Capsid, shell assembling in the underlying potential energy surfaces and disclination in fivelings and related shapes such as pyramidal copper and other metal nanowires. Properties A pentagonal pyramid has six vertices, ten edges, and six faces. One of its faces is pentagon, a ''base'' of the pyramid; five others are triangles. Five of the edges make up the pentagon by connecting its five vertices, and the other fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tabletop Role-playing Games
A tabletop role-playing game (TTRPG or TRPG), also known as a pen-and-paper role-playing game, is a kind of role-playing game (RPG) in which the participants describe their characters' actions through speech and sometimes movements. Participants determine the actions of their characters based on their characterization, and the actions succeed or fail according to a set formal system of rules and guidelines, usually involving randomization (such as through dice). Within the rules, players have the freedom to improvise, and their choices shape the direction and outcome of the game. Neither pen and paper nor a table are strictly necessary for a game to count as a TTRPG; rather, the terms ''pen-and-paper'' and ''tabletop'' are typically used to distinguish this format of RPG from role-playing video games or live action role-playing games. Online play of TTRPGs through videoconferencing has become common since the COVID-19 pandemic. Some common examples of tabletop role-playing games in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
D20 System
The d20 System is a role-playing game system published in 2000 by Wizards of the Coast, originally developed for the Editions of Dungeons & Dragons#Dungeons & Dragons 3rd edition, 3rd edition of ''Dungeons & Dragons''. The system is named after the Dice#Common variations, 20-sided dice which are central to the core mechanics of many actions in the game. Much of the d20 System was released as the System Reference Document (SRD) under the Open Game License (OGL) as Open gaming, Open Game Content (OGC), which allows commercial and non-commercial publishers to release modifications or supplements to the system without paying for the use of the system's associated intellectual property, which is owned by Wizards of the Coast. The original impetus for the open licensing of the d20 System involved the economics of producing role-playing games (RPGs). Game supplements suffered significantly more diminished sales over time than the core books required to play the game. Ryan Dancey, Brand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cartography
Cartography (; from , 'papyrus, sheet of paper, map'; and , 'write') is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an imagined reality) can be modeled in ways that communicate spatial information effectively. The fundamental objectives of traditional cartography are to: * Set the map's agenda and select traits of the object to be mapped. This is the concern of map editing. Traits may be physical, such as roads or land masses, or may be abstract, such as toponyms or political boundaries. * Represent the terrain of the mapped object on flat media. This is the concern of map projections. * Eliminate the mapped object's characteristics that are irrelevant to the map's purpose. This is the concern of Cartographic generalization, generalization. * Reduce the complexity of the characteristics that will be mapped. This is also the concern of generalization. * Orchestrate the elements ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Capsid
A capsid is the protein shell of a virus, enclosing its genetic material. It consists of several oligomeric (repeating) structural subunits made of protein called protomers. The observable 3-dimensional morphological subunits, which may or may not correspond to individual proteins, are called capsomeres. The proteins making up the capsid are called capsid proteins or viral coat proteins (VCP). The virus genomic component inside the capsid, along with occasionally present virus core protein, is called the virus core. The capsid and core together are referred to as a nucleocapsid (cf. also virion). Capsids are broadly classified according to their structure. The majority of the viruses have capsids with either helical or icosahedral structure. Some viruses, such as bacteriophages, have developed more complicated structures due to constraints of elasticity and electrostatics. The icosahedral shape, which has 20 equilateral triangular faces, approximates a sphere, while th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from "tetrahedral complex") and a polytetrahedron, being bounded by tetrahedral Cell (geometry), cells. The 600-cell's boundary is composed of 600 Tetrahedron, tetrahedral Cell (mathematics), cells with 20 meeting at each vertex. Together they form 1200 triangular faces, 720 edges, and 120 vertices. It is the 4-Four-dimensional space#Dimensional analogy, dimensional analogue of the icosahedron, since it has five Tetrahedron, tetrahedra meeting at every edge, just as the icosahedron has five triangles meeting at every vertex. Its dual polytope is the 120-cell. Geometry The 600-cell is the fifth in the sequence of 6 convex regular 4-polytopes (in order of complexity and size at the same radius). It can be deconstructed into twenty-five overla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Polytope
In elementary geometry, a polytope is a geometric object with flat sides ('' faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an -dimensional polytope or -polytope. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope. In this context, "flat sides" means that the sides of a -polytope consist of -polytopes that may have -polytopes in common. Some theories further generalize the idea to include such objects as unbounded apeirotopes and tessellations, decompositions or tilings of curved manifolds including spherical polyhedra, and set-theoretic abstract polytopes. Polytopes of more than three dimensions were first discovered by Ludwig Schläfli before 1853, who called such a figure a polyschem. The German term ''Polytop'' was coined by the mathematician Reinhold Hoppe, and was introduced to English mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Johnson Solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, solids with such a property: the first solids are the Pyramid (geometry), pyramids, Cupola (geometry), cupolas, and a Rotunda (geometry), rotunda; some of the solids may be constructed by attaching with those previous solids, whereas others may not. Definition and background A Johnson solid is a convex polyhedron whose faces are all regular polygons. The convex polyhedron means as bounded intersections of finitely many Half-space (geometry), half-spaces, or as the convex hull of finitely many points. Although there is no restriction that any given regular polygon cannot be a face of a Johnson solid, some authors required that Johnson solids are not Uniform polyhedron, uniform. This means that a Johnson solid is not a Platonic solid, Arc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Faceting
Stella octangula as a faceting of the cube In geometry, faceting (also spelled facetting) is the process of removing parts of a polygon, polyhedron or polytope, without creating any new Vertex (geometry), vertices. New edges of a faceted polyhedron may be created along face diagonals or internal space diagonals. A ''faceted polyhedron'' will have two faces on each edge and creates new polyhedra or compounds of polyhedra. Faceting is the reciprocal or duality (mathematics), dual process to ''stellation''. For every stellation of some convex polytope, there exists a dual faceting of the dual polytope. Faceted polygons For example, a regular pentagon has one symmetry faceting, the pentagram, and the regular hexagon has two symmetric facetings, one as a polygon, and one as a compound of two triangles. Faceted polyhedra The regular icosahedron can be faceted into three regular Kepler–Poinsot polyhedron, Kepler–Poinsot polyhedra: small stellated dodecahedron, great dodeca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |