Optics on:
[Wikipedia]
[Google]
[Amazon]
 Optics is the branch of
Optics is the branch of
 Optics began with the development of lenses by the
Optics began with the development of lenses by the  During the
During the
 Classical optics is divided into two main branches: geometrical (or ray) optics and physical (or wave) optics. In geometrical optics, light is considered to travel in straight lines, while in physical optics, light is considered as an electromagnetic wave.
Geometrical optics can be viewed as an approximation of physical optics that applies when the wavelength of the light used is much smaller than the size of the optical elements in the system being modelled.
Classical optics is divided into two main branches: geometrical (or ray) optics and physical (or wave) optics. In geometrical optics, light is considered to travel in straight lines, while in physical optics, light is considered as an electromagnetic wave.
Geometrical optics can be viewed as an approximation of physical optics that applies when the wavelength of the light used is much smaller than the size of the optical elements in the system being modelled.
 ''Geometrical optics'', or ''ray optics'', describes the propagation of light in terms of "rays" which travel in straight lines, and whose paths are governed by the laws of reflection and refraction at interfaces between different media. These laws were discovered empirically as far back as 984 AD and have been used in the design of optical components and instruments from then until the present day. They can be summarised as follows:
When a ray of light hits the boundary between two transparent materials, it is divided into a reflected and a refracted ray.
* The law of reflection says that the reflected ray lies in the plane of incidence, and the angle of reflection equals the angle of incidence.
* The law of refraction says that the refracted ray lies in the plane of incidence, and the sine of the angle of incidence divided by the sine of the angle of refraction is a constant: where is a constant for any two materials and a given wavelength of light. If the first material is air or vacuum, is the
''Geometrical optics'', or ''ray optics'', describes the propagation of light in terms of "rays" which travel in straight lines, and whose paths are governed by the laws of reflection and refraction at interfaces between different media. These laws were discovered empirically as far back as 984 AD and have been used in the design of optical components and instruments from then until the present day. They can be summarised as follows:
When a ray of light hits the boundary between two transparent materials, it is divided into a reflected and a refracted ray.
* The law of reflection says that the reflected ray lies in the plane of incidence, and the angle of reflection equals the angle of incidence.
* The law of refraction says that the refracted ray lies in the plane of incidence, and the sine of the angle of incidence divided by the sine of the angle of refraction is a constant: where is a constant for any two materials and a given wavelength of light. If the first material is air or vacuum, is the
 Reflections can be divided into two types: specular reflection and diffuse reflection. Specular reflection describes the gloss of surfaces such as mirrors, which reflect light in a simple, predictable way. This allows for the production of reflected images that can be associated with an actual ( real) or extrapolated ( virtual) location in space. Diffuse reflection describes non-glossy materials, such as paper or rock. The reflections from these surfaces can only be described statistically, with the exact distribution of the reflected light depending on the microscopic structure of the material. Many diffuse reflectors are described or can be approximated by Lambert's cosine law, which describes surfaces that have equal luminance when viewed from any angle. Glossy surfaces can give both specular and diffuse reflection.
In specular reflection, the direction of the reflected ray is determined by the angle the incident ray makes with the
Reflections can be divided into two types: specular reflection and diffuse reflection. Specular reflection describes the gloss of surfaces such as mirrors, which reflect light in a simple, predictable way. This allows for the production of reflected images that can be associated with an actual ( real) or extrapolated ( virtual) location in space. Diffuse reflection describes non-glossy materials, such as paper or rock. The reflections from these surfaces can only be described statistically, with the exact distribution of the reflected light depending on the microscopic structure of the material. Many diffuse reflectors are described or can be approximated by Lambert's cosine law, which describes surfaces that have equal luminance when viewed from any angle. Glossy surfaces can give both specular and diffuse reflection.
In specular reflection, the direction of the reflected ray is determined by the angle the incident ray makes with the
 Refraction occurs when light travels through an area of space that has a changing index of refraction; this principle allows for lenses and the focusing of light. The simplest case of refraction occurs when there is an interface between a uniform medium with index of refraction and another medium with index of refraction . In such situations, Snell's Law describes the resulting deflection of the light ray:
where and are the angles between the normal (to the interface) and the incident and refracted waves, respectively.
The index of refraction of a medium is related to the speed, , of light in that medium by
where is the speed of light in vacuum.
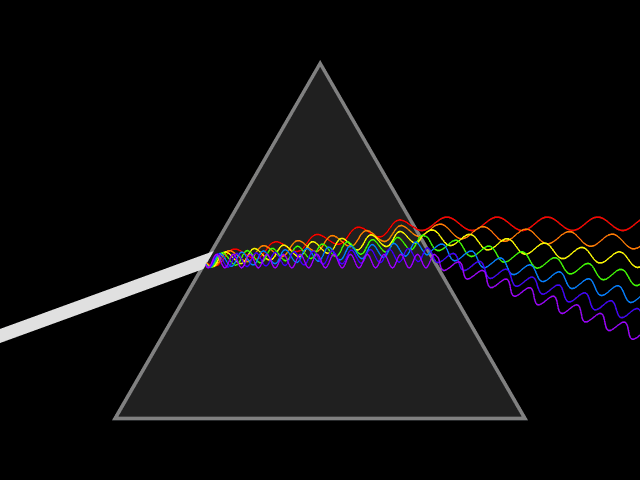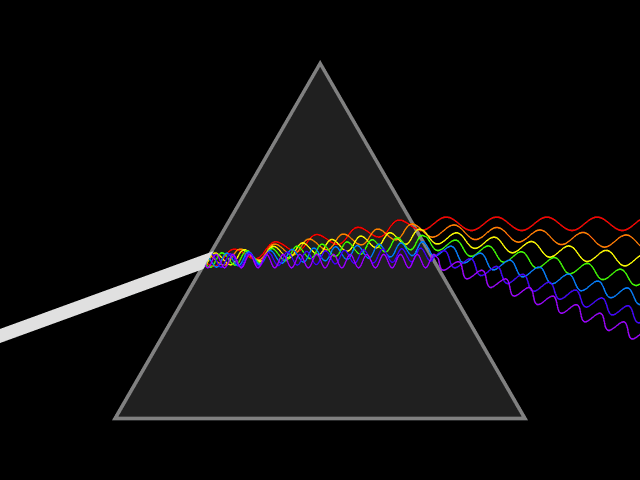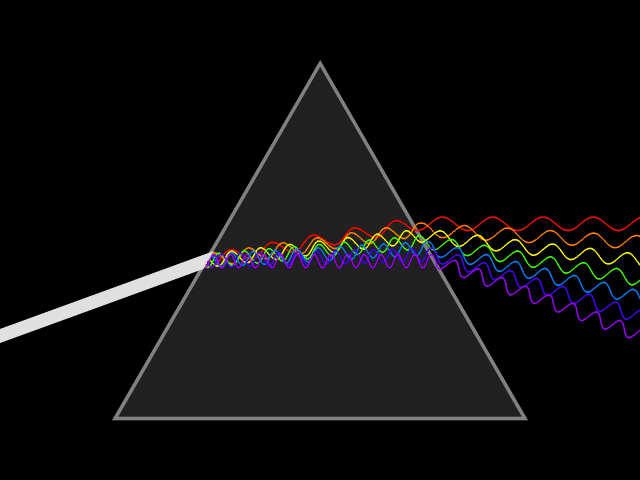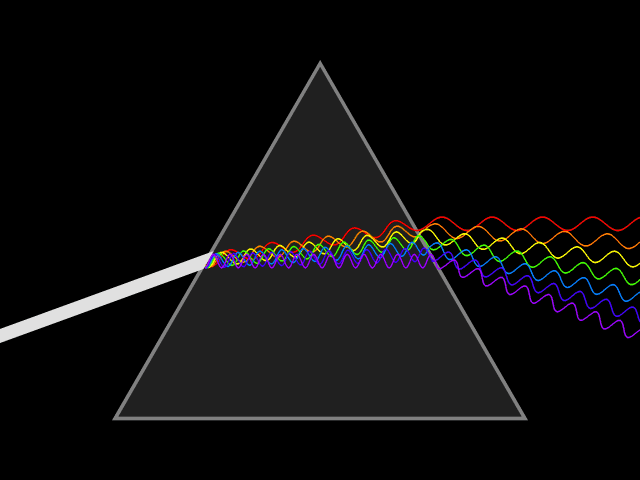
Snell's Law can be used to predict the deflection of light rays as they pass through linear media as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a prism results in the light ray being deflected depending on the shape and orientation of the prism. In most materials, the index of refraction varies with the frequency of the light, known as dispersion. Taking this into account, Snell's Law can be used to predict how a prism will disperse light into a spectrum. The discovery of this phenomenon when passing light through a prism is famously attributed to Isaac Newton.
Some media have an index of refraction which varies gradually with position and, therefore, light rays in the medium are curved. This effect is responsible for mirages seen on hot days: a change in index of refraction air with height causes light rays to bend, creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Optical materials with varying indexes of refraction are called gradient-index (GRIN) materials. Such materials are used to make gradient-index optics.
For light rays travelling from a material with a high index of refraction to a material with a low index of refraction, Snell's law predicts that there is no when is large. In this case, no transmission occurs; all the light is reflected. This phenomenon is called total internal reflection and allows for fibre optics technology. As light travels down an optical fibre, it undergoes total internal reflection allowing for essentially no light to be lost over the length of the cable.
Refraction occurs when light travels through an area of space that has a changing index of refraction; this principle allows for lenses and the focusing of light. The simplest case of refraction occurs when there is an interface between a uniform medium with index of refraction and another medium with index of refraction . In such situations, Snell's Law describes the resulting deflection of the light ray:
where and are the angles between the normal (to the interface) and the incident and refracted waves, respectively.
The index of refraction of a medium is related to the speed, , of light in that medium by
where is the speed of light in vacuum.
Snell's Law can be used to predict the deflection of light rays as they pass through linear media as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a prism results in the light ray being deflected depending on the shape and orientation of the prism. In most materials, the index of refraction varies with the frequency of the light, known as dispersion. Taking this into account, Snell's Law can be used to predict how a prism will disperse light into a spectrum. The discovery of this phenomenon when passing light through a prism is famously attributed to Isaac Newton.
Some media have an index of refraction which varies gradually with position and, therefore, light rays in the medium are curved. This effect is responsible for mirages seen on hot days: a change in index of refraction air with height causes light rays to bend, creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Optical materials with varying indexes of refraction are called gradient-index (GRIN) materials. Such materials are used to make gradient-index optics.
For light rays travelling from a material with a high index of refraction to a material with a low index of refraction, Snell's law predicts that there is no when is large. In this case, no transmission occurs; all the light is reflected. This phenomenon is called total internal reflection and allows for fibre optics technology. As light travels down an optical fibre, it undergoes total internal reflection allowing for essentially no light to be lost over the length of the cable.
 Incoming parallel rays are focused by a converging lens onto a spot one focal length from the lens, on the far side of the lens. This is called the rear focal point of the lens. Rays from an object at a finite distance are focused further from the lens than the focal distance; the closer the object is to the lens, the further the image is from the lens.
With diverging lenses, incoming parallel rays diverge after going through the lens, in such a way that they seem to have originated at a spot one focal length in front of the lens. This is the lens's front focal point. Rays from an object at a finite distance are associated with a virtual image that is closer to the lens than the focal point, and on the same side of the lens as the object. The closer the object is to the lens, the closer the virtual image is to the lens. As with mirrors, upright images produced by a single lens are virtual, while inverted images are real.
Lenses suffer from aberrations that distort images. ''Monochromatic aberrations'' occur because the geometry of the lens does not perfectly direct rays from each object point to a single point on the image, while chromatic aberration occurs because the index of refraction of the lens varies with the wavelength of the light.
Incoming parallel rays are focused by a converging lens onto a spot one focal length from the lens, on the far side of the lens. This is called the rear focal point of the lens. Rays from an object at a finite distance are focused further from the lens than the focal distance; the closer the object is to the lens, the further the image is from the lens.
With diverging lenses, incoming parallel rays diverge after going through the lens, in such a way that they seem to have originated at a spot one focal length in front of the lens. This is the lens's front focal point. Rays from an object at a finite distance are associated with a virtual image that is closer to the lens than the focal point, and on the same side of the lens as the object. The closer the object is to the lens, the closer the virtual image is to the lens. As with mirrors, upright images produced by a single lens are virtual, while inverted images are real.
Lenses suffer from aberrations that distort images. ''Monochromatic aberrations'' occur because the geometry of the lens does not perfectly direct rays from each object point to a single point on the image, while chromatic aberration occurs because the index of refraction of the lens varies with the wavelength of the light.

 Since the HuygensŌĆōFresnel principle states that every point of a wavefront is associated with the production of a new disturbance, it is possible for a wavefront to interfere with itself constructively or destructively at different locations producing bright and dark fringes in regular and predictable patterns. Interferometry is the science of measuring these patterns, usually as a means of making precise determinations of distances or angular resolutions. The Michelson interferometer was a famous instrument which used interference effects to accurately measure the speed of light.
The appearance of thin films and coatings is directly affected by interference effects. Antireflective coatings use destructive interference to reduce the reflectivity of the surfaces they coat, and can be used to minimise glare and unwanted reflections. The simplest case is a single layer with a thickness of one-fourth the wavelength of incident light. The reflected wave from the top of the film and the reflected wave from the film/material interface are then exactly 180┬░ out of phase, causing destructive interference. The waves are only exactly out of phase for one wavelength, which would typically be chosen to be near the centre of the visible spectrum, around 550 nm. More complex designs using multiple layers can achieve low reflectivity over a broad band, or extremely low reflectivity at a single wavelength.
Constructive interference in thin films can create a strong reflection of light in a range of wavelengths, which can be narrow or broad depending on the design of the coating. These films are used to make dielectric mirrors, interference filters, heat reflectors, and filters for colour separation in colour television cameras. This interference effect is also what causes the colourful rainbow patterns seen in oil slicks.
Since the HuygensŌĆōFresnel principle states that every point of a wavefront is associated with the production of a new disturbance, it is possible for a wavefront to interfere with itself constructively or destructively at different locations producing bright and dark fringes in regular and predictable patterns. Interferometry is the science of measuring these patterns, usually as a means of making precise determinations of distances or angular resolutions. The Michelson interferometer was a famous instrument which used interference effects to accurately measure the speed of light.
The appearance of thin films and coatings is directly affected by interference effects. Antireflective coatings use destructive interference to reduce the reflectivity of the surfaces they coat, and can be used to minimise glare and unwanted reflections. The simplest case is a single layer with a thickness of one-fourth the wavelength of incident light. The reflected wave from the top of the film and the reflected wave from the film/material interface are then exactly 180┬░ out of phase, causing destructive interference. The waves are only exactly out of phase for one wavelength, which would typically be chosen to be near the centre of the visible spectrum, around 550 nm. More complex designs using multiple layers can achieve low reflectivity over a broad band, or extremely low reflectivity at a single wavelength.
Constructive interference in thin films can create a strong reflection of light in a range of wavelengths, which can be narrow or broad depending on the design of the coating. These films are used to make dielectric mirrors, interference filters, heat reflectors, and filters for colour separation in colour television cameras. This interference effect is also what causes the colourful rainbow patterns seen in oil slicks.
 Diffraction is the process by which light interference is most commonly observed. The effect was first described in 1665 by
Diffraction is the process by which light interference is most commonly observed. The effect was first described in 1665 by
 Refractive processes take place in the physical optics limit, where the wavelength of light is similar to other distances, as a kind of scattering. The simplest type of scattering is Thomson scattering which occurs when electromagnetic waves are deflected by single particles. In the limit of Thomson scattering, in which the wavelike nature of light is evident, light is dispersed independent of the frequency, in contrast to Compton scattering which is frequency-dependent and strictly a quantum mechanical process, involving the nature of light as particles. In a statistical sense, elastic scattering of light by numerous particles much smaller than the wavelength of the light is a process known as Rayleigh scattering while the similar process for scattering by particles that are similar or larger in wavelength is known as Mie scattering with the Tyndall effect being a commonly observed result. A small proportion of light scattering from atoms or molecules may undergo Raman scattering, wherein the frequency changes due to excitation of the atoms and molecules. Brillouin scattering occurs when the frequency of light changes due to local changes with time and movements of a dense material.
Dispersion occurs when different frequencies of light have different phase velocities, due either to material properties (''material dispersion'') or to the geometry of an
Refractive processes take place in the physical optics limit, where the wavelength of light is similar to other distances, as a kind of scattering. The simplest type of scattering is Thomson scattering which occurs when electromagnetic waves are deflected by single particles. In the limit of Thomson scattering, in which the wavelike nature of light is evident, light is dispersed independent of the frequency, in contrast to Compton scattering which is frequency-dependent and strictly a quantum mechanical process, involving the nature of light as particles. In a statistical sense, elastic scattering of light by numerous particles much smaller than the wavelength of the light is a process known as Rayleigh scattering while the similar process for scattering by particles that are similar or larger in wavelength is known as Mie scattering with the Tyndall effect being a commonly observed result. A small proportion of light scattering from atoms or molecules may undergo Raman scattering, wherein the frequency changes due to excitation of the atoms and molecules. Brillouin scattering occurs when the frequency of light changes due to local changes with time and movements of a dense material.
Dispersion occurs when different frequencies of light have different phase velocities, due either to material properties (''material dispersion'') or to the geometry of an  Material dispersion is often characterised by the Abbe number, which gives a simple measure of dispersion based on the index of refraction at three specific wavelengths. Waveguide dispersion is dependent on the propagation constant. Both kinds of dispersion cause changes in the group characteristics of the wave, the features of the wave packet that change with the same frequency as the amplitude of the electromagnetic wave. "Group velocity dispersion" manifests as a spreading-out of the signal "envelope" of the radiation and can be quantified with a group dispersion delay parameter:
where is the group velocity. For a uniform medium, the group velocity is
where is the index of refraction and is the speed of light in a vacuum. This gives a simpler form for the dispersion delay parameter:
If is less than zero, the medium is said to have ''positive dispersion'' or normal dispersion. If is greater than zero, the medium has ''negative dispersion''. If a light pulse is propagated through a normally dispersive medium, the result is the higher frequency components slow down more than the lower frequency components. The pulse therefore becomes ''positively chirped'', or ''up-chirped'', increasing in frequency with time. This causes the spectrum coming out of a prism to appear with red light the least refracted and blue/violet light the most refracted. Conversely, if a pulse travels through an anomalously (negatively) dispersive medium, high-frequency components travel faster than the lower ones, and the pulse becomes ''negatively chirped'', or ''down-chirped'', decreasing in frequency with time.
The result of group velocity dispersion, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on optical fibres, since if dispersion is too high, a group of pulses representing information will each spread in time and merge, making it impossible to extract the signal.
Material dispersion is often characterised by the Abbe number, which gives a simple measure of dispersion based on the index of refraction at three specific wavelengths. Waveguide dispersion is dependent on the propagation constant. Both kinds of dispersion cause changes in the group characteristics of the wave, the features of the wave packet that change with the same frequency as the amplitude of the electromagnetic wave. "Group velocity dispersion" manifests as a spreading-out of the signal "envelope" of the radiation and can be quantified with a group dispersion delay parameter:
where is the group velocity. For a uniform medium, the group velocity is
where is the index of refraction and is the speed of light in a vacuum. This gives a simpler form for the dispersion delay parameter:
If is less than zero, the medium is said to have ''positive dispersion'' or normal dispersion. If is greater than zero, the medium has ''negative dispersion''. If a light pulse is propagated through a normally dispersive medium, the result is the higher frequency components slow down more than the lower frequency components. The pulse therefore becomes ''positively chirped'', or ''up-chirped'', increasing in frequency with time. This causes the spectrum coming out of a prism to appear with red light the least refracted and blue/violet light the most refracted. Conversely, if a pulse travels through an anomalously (negatively) dispersive medium, high-frequency components travel faster than the lower ones, and the pulse becomes ''negatively chirped'', or ''down-chirped'', decreasing in frequency with time.
The result of group velocity dispersion, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on optical fibres, since if dispersion is too high, a group of pulses representing information will each spread in time and merge, making it impossible to extract the signal.
In the leftmost figure above, the and components of the light wave are in phase. In this case, the ratio of their strengths is constant, so the direction of the electric vector (the vector sum of these two components) is constant. Since the tip of the vector traces out a single line in the plane, this special case is called linear polarisation. The direction of this line depends on the relative amplitudes of the two components.
In the middle figure, the two orthogonal components have the same amplitudes and are 90┬░ out of phase. In this case, one component is zero when the other component is at maximum or minimum amplitude. There are two possible phase relationships that satisfy this requirement: the component can be 90┬░ ahead of the component or it can be 90┬░ behind the component. In this special case, the electric vector traces out a circle in the plane, so this polarisation is called circular polarisation. The rotation direction in the circle depends on which of the two-phase relationships exists and corresponds to ''right-hand circular polarisation'' and ''left-hand circular polarisation''.
In all other cases, where the two components either do not have the same amplitudes and/or their phase difference is neither zero nor a multiple of 90┬░, the polarisation is called elliptical polarisation because the electric vector traces out an
 Media that reduce the amplitude of certain polarisation modes are called ''dichroic'', with devices that block nearly all of the radiation in one mode known as ''polarising filters'' or simply " polarisers". Malus' law, which is named after ├ētienne-Louis Malus, says that when a perfect polariser is placed in a linear polarised beam of light, the intensity, , of the light that passes through is given by
where is the initial intensity, and is the angle between the light's initial polarisation direction and the axis of the polariser.
A beam of unpolarised light can be thought of as containing a uniform mixture of linear polarisations at all possible angles. Since the average value of is 1/2, the transmission coefficient becomes
In practice, some light is lost in the polariser and the actual transmission of unpolarised light will be somewhat lower than this, around 38% for Polaroid-type polarisers but considerably higher (>49.9%) for some birefringent prism types.
In addition to birefringence and dichroism in extended media, polarisation effects can also occur at the (reflective) interface between two materials of different refractive index. These effects are treated by the Fresnel equations. Part of the wave is transmitted and part is reflected, with the ratio depending on the angle of incidence and the angle of refraction. In this way, physical optics recovers Brewster's angle. When light reflects from a thin film on a surface, interference between the reflections from the film's surfaces can produce polarisation in the reflected and transmitted light.
Media that reduce the amplitude of certain polarisation modes are called ''dichroic'', with devices that block nearly all of the radiation in one mode known as ''polarising filters'' or simply " polarisers". Malus' law, which is named after ├ētienne-Louis Malus, says that when a perfect polariser is placed in a linear polarised beam of light, the intensity, , of the light that passes through is given by
where is the initial intensity, and is the angle between the light's initial polarisation direction and the axis of the polariser.
A beam of unpolarised light can be thought of as containing a uniform mixture of linear polarisations at all possible angles. Since the average value of is 1/2, the transmission coefficient becomes
In practice, some light is lost in the polariser and the actual transmission of unpolarised light will be somewhat lower than this, around 38% for Polaroid-type polarisers but considerably higher (>49.9%) for some birefringent prism types.
In addition to birefringence and dichroism in extended media, polarisation effects can also occur at the (reflective) interface between two materials of different refractive index. These effects are treated by the Fresnel equations. Part of the wave is transmitted and part is reflected, with the ratio depending on the angle of incidence and the angle of refraction. In this way, physical optics recovers Brewster's angle. When light reflects from a thin film on a surface, interference between the reflections from the film's surfaces can produce polarisation in the reflected and transmitted light.
 Most sources of electromagnetic radiation contain a large number of atoms or molecules that emit light. The orientation of the electric fields produced by these emitters may not be
Most sources of electromagnetic radiation contain a large number of atoms or molecules that emit light. The orientation of the electric fields produced by these emitters may not be
 A laser is a device that emits light, a kind of electromagnetic radiation, through a process called '' stimulated emission''. The term ''laser'' is an
A laser is a device that emits light, a kind of electromagnetic radiation, through a process called '' stimulated emission''. The term ''laser'' is an
 The human eye functions by focusing light onto a layer of photoreceptor cells called the retina, which forms the inner lining of the back of the eye. The focusing is accomplished by a series of transparent media. Light entering the eye passes first through the cornea, which provides much of the eye's optical power. The light then continues through the fluid just behind the corneaŌĆöthe anterior chamber, then passes through the pupil. The light then passes through the lens, which focuses the light further and allows adjustment of focus. The light then passes through the main body of fluid in the eyeŌĆöthe vitreous humour, and reaches the retina. The cells in the retina line the back of the eye, except for where the optic nerve exits; this results in a blind spot.
There are two types of photoreceptor cells, rods and cones, which are sensitive to different aspects of light. Rod cells are sensitive to the intensity of light over a wide frequency range, thus are responsible for black-and-white vision. Rod cells are not present on the fovea, the area of the retina responsible for central vision, and are not as responsive as cone cells to spatial and temporal changes in light. There are, however, twenty times more rod cells than cone cells in the retina because the rod cells are present across a wider area. Because of their wider distribution, rods are responsible for peripheral vision.
In contrast, cone cells are less sensitive to the overall intensity of light, but come in three varieties that are sensitive to different frequency-ranges and thus are used in the perception of
The human eye functions by focusing light onto a layer of photoreceptor cells called the retina, which forms the inner lining of the back of the eye. The focusing is accomplished by a series of transparent media. Light entering the eye passes first through the cornea, which provides much of the eye's optical power. The light then continues through the fluid just behind the corneaŌĆöthe anterior chamber, then passes through the pupil. The light then passes through the lens, which focuses the light further and allows adjustment of focus. The light then passes through the main body of fluid in the eyeŌĆöthe vitreous humour, and reaches the retina. The cells in the retina line the back of the eye, except for where the optic nerve exits; this results in a blind spot.
There are two types of photoreceptor cells, rods and cones, which are sensitive to different aspects of light. Rod cells are sensitive to the intensity of light over a wide frequency range, thus are responsible for black-and-white vision. Rod cells are not present on the fovea, the area of the retina responsible for central vision, and are not as responsive as cone cells to spatial and temporal changes in light. There are, however, twenty times more rod cells than cone cells in the retina because the rod cells are present across a wider area. Because of their wider distribution, rods are responsible for peripheral vision.
In contrast, cone cells are less sensitive to the overall intensity of light, but come in three varieties that are sensitive to different frequency-ranges and thus are used in the perception of
 Optical illusions (also called visual illusions) are characterized by visually perceived images that differ from objective reality. The information gathered by the eye is processed in the brain to give a percept that differs from the object being imaged. Optical illusions can be the result of a variety of phenomena including physical effects that create images that are different from the objects that make them, the physiological effects on the eyes and brain of excessive stimulation (e.g. brightness, tilt, colour, movement), and cognitive illusions where the eye and brain make unconscious inferences.
Cognitive illusions include some which result from the unconscious misapplication of certain optical principles. For example, the Ames room, Hering, M├╝ller-Lyer, Orbison, Ponzo, Sander, and Wundt illusions all rely on the suggestion of the appearance of distance by using converging and diverging lines, in the same way that parallel light rays (or indeed any set of parallel lines) appear to converge at a vanishing point at infinity in two-dimensionally rendered images with artistic perspective. This suggestion is also responsible for the famous moon illusion where the moon, despite having essentially the same angular size, appears much larger near the
Optical illusions (also called visual illusions) are characterized by visually perceived images that differ from objective reality. The information gathered by the eye is processed in the brain to give a percept that differs from the object being imaged. Optical illusions can be the result of a variety of phenomena including physical effects that create images that are different from the objects that make them, the physiological effects on the eyes and brain of excessive stimulation (e.g. brightness, tilt, colour, movement), and cognitive illusions where the eye and brain make unconscious inferences.
Cognitive illusions include some which result from the unconscious misapplication of certain optical principles. For example, the Ames room, Hering, M├╝ller-Lyer, Orbison, Ponzo, Sander, and Wundt illusions all rely on the suggestion of the appearance of distance by using converging and diverging lines, in the same way that parallel light rays (or indeed any set of parallel lines) appear to converge at a vanishing point at infinity in two-dimensionally rendered images with artistic perspective. This suggestion is also responsible for the famous moon illusion where the moon, despite having essentially the same angular size, appears much larger near the

 The optics of photography involves both lenses and the medium in which the electromagnetic radiation is recorded, whether it be a plate,
The optics of photography involves both lenses and the medium in which the electromagnetic radiation is recorded, whether it be a plate,
 The unique optical properties of the atmosphere cause a wide range of spectacular optical phenomena. The blue colour of the sky is a direct result of Rayleigh scattering which redirects higher frequency (blue) sunlight back into the field of view of the observer. Because blue light is scattered more easily than red light, the sun takes on a reddish hue when it is observed through a thick atmosphere, as during a sunrise or
The unique optical properties of the atmosphere cause a wide range of spectacular optical phenomena. The blue colour of the sky is a direct result of Rayleigh scattering which redirects higher frequency (blue) sunlight back into the field of view of the observer. Because blue light is scattered more easily than red light, the sun takes on a reddish hue when it is observed through a thick atmosphere, as during a sunrise or
Light and Matter
ŌĆō an open-source textbook, containing a treatment of optics in ch. 28ŌĆō32
Optics2001
ŌĆō Optics library and community
Fundamental Optics
ŌĆō Melles Griot Technical Guide
Physics of Light and Optics
ŌĆō
Optics for PV
ŌĆō a step-by-step introduction to classical optics ;Further reading
b
;Societies * European Optical Society ŌĆ
link
* The Optical Society (OSA) ŌĆ
link
* SPIE ŌĆ
link
* European Photonics Industry Consortium ŌĆ
link
{{Authority control > > Applied and interdisciplinary physics Atomic, molecular, and optical physics Natural philosophy
 Optics is the branch of
Optics is the branch of physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
that studies the behaviour and properties of light
Light, visible light, or visible radiation is electromagnetic radiation that can be visual perception, perceived by the human eye. Visible light spans the visible spectrum and is usually defined as having wavelengths in the range of 400ŌĆō ...
, including its interactions with matter
In classical physics and general chemistry, matter is any substance that has mass and takes up space by having volume. All everyday objects that can be touched are ultimately composed of atoms, which are made up of interacting subatomic pa ...
and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet
Ultraviolet radiation, also known as simply UV, is electromagnetic radiation of wavelengths of 10ŌĆō400 nanometers, shorter than that of visible light, but longer than X-rays. UV radiation is present in sunlight and constitutes about 10% of ...
, and infrared
Infrared (IR; sometimes called infrared light) is electromagnetic radiation (EMR) with wavelengths longer than that of visible light but shorter than microwaves. The infrared spectral band begins with the waves that are just longer than those ...
light. Light is a type of electromagnetic radiation
In physics, electromagnetic radiation (EMR) is a self-propagating wave of the electromagnetic field that carries momentum and radiant energy through space. It encompasses a broad spectrum, classified by frequency or its inverse, wavelength ...
, and other forms of electromagnetic radiation such as X-ray
An X-ray (also known in many languages as R├Čntgen radiation) is a form of high-energy electromagnetic radiation with a wavelength shorter than those of ultraviolet rays and longer than those of gamma rays. Roughly, X-rays have a wavelength ran ...
s, microwave
Microwave is a form of electromagnetic radiation with wavelengths shorter than other radio waves but longer than infrared waves. Its wavelength ranges from about one meter to one millimeter, corresponding to frequency, frequencies between 300&n ...
s, and radio waves exhibit similar properties.
Most optical phenomena can be accounted for by using the classical electromagnetic description of light, however complete electromagnetic descriptions of light are often difficult to apply in practice. Practical optics is usually done using simplified models. The most common of these, geometric optics
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician ...
, treats light as a collection of rays that travel in straight lines and bend when they pass through or reflect from surfaces. Physical optics is a more comprehensive model of light, which includes wave
In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance (change from List of types of equilibrium, equilibrium) of one or more quantities. ''Periodic waves'' oscillate repeatedly about an equilibrium ...
effects such as diffraction
Diffraction is the deviation of waves from straight-line propagation without any change in their energy due to an obstacle or through an aperture. The diffracting object or aperture effectively becomes a secondary source of the Wave propagation ...
and interference that cannot be accounted for in geometric optics. Historically, the ray-based model of light was developed first, followed by the wave model of light. Progress in electromagnetic theory in the 19th century led to the discovery that light waves were in fact electromagnetic radiation.
Some phenomena depend on light having both wave-like and particle-like properties. Explanation of these effects requires quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
. When considering light's particle-like properties, the light is modelled as a collection of particles called "photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s". Quantum optics deals with the application of quantum mechanics to optical systems.
Optical science is relevant to and studied in many related disciplines including astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
, various engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
fields, photography
Photography is the visual arts, art, application, and practice of creating images by recording light, either electronically by means of an image sensor, or chemically by means of a light-sensitive material such as photographic film. It is empl ...
, and medicine
Medicine is the science and Praxis (process), practice of caring for patients, managing the Medical diagnosis, diagnosis, prognosis, Preventive medicine, prevention, therapy, treatment, Palliative care, palliation of their injury or disease, ...
(particularly ophthalmology
Ophthalmology (, ) is the branch of medicine that deals with the diagnosis, treatment, and surgery of eye diseases and disorders.
An ophthalmologist is a physician who undergoes subspecialty training in medical and surgical eye care. Following a ...
and optometry
Optometry is the healthcare practice concerned with examining the eyes for visual defects, prescribing corrective lenses, and detecting eye abnormalities.
In the United States and Canada, optometrists are those that hold a post-baccalaureate f ...
, in which it is called physiological optics). Practical applications of optics are found in a variety of technologies and everyday objects, including mirrors, lenses, telescopes
A telescope is a device used to observe distant objects by their emission, Absorption (electromagnetic radiation), absorption, or Reflection (physics), reflection of electromagnetic radiation. Originally, it was an optical instrument using len ...
, microscope
A microscope () is a laboratory equipment, laboratory instrument used to examine objects that are too small to be seen by the naked eye. Microscopy is the science of investigating small objects and structures using a microscope. Microscopic ...
s, laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of electromagnetic radiation. The word ''laser'' originated as an acronym for light amplification by stimulated emission of radi ...
s, and fibre optics.
History
 Optics began with the development of lenses by the
Optics began with the development of lenses by the ancient Egypt
Ancient Egypt () was a cradle of civilization concentrated along the lower reaches of the Nile River in Northeast Africa. It emerged from prehistoric Egypt around 3150BC (according to conventional Egyptian chronology), when Upper and Lower E ...
ians and Mesopotamia
Mesopotamia is a historical region of West Asia situated within the TigrisŌĆōEuphrates river system, in the northern part of the Fertile Crescent. Today, Mesopotamia is known as present-day Iraq and forms the eastern geographic boundary of ...
ns. The earliest known lenses, made from polished crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
, often quartz
Quartz is a hard, crystalline mineral composed of silica (silicon dioxide). The Atom, atoms are linked in a continuous framework of SiO4 siliconŌĆōoxygen Tetrahedral molecular geometry, tetrahedra, with each oxygen being shared between two tet ...
, date from as early as 2000 BC from Crete
Crete ( ; , Modern Greek, Modern: , Ancient Greek, Ancient: ) is the largest and most populous of the Greek islands, the List of islands by area, 88th largest island in the world and the List of islands in the Mediterranean#By area, fifth la ...
(Archaeological Museum of Heraclion, Greece). Lenses from Rhodes
Rhodes (; ) is the largest of the Dodecanese islands of Greece and is their historical capital; it is the List of islands in the Mediterranean#By area, ninth largest island in the Mediterranean Sea. Administratively, the island forms a separ ...
date around 700 BC, as do Assyria
Assyria (Neo-Assyrian cuneiform: , ''m─üt A┼Ī┼Īur'') was a major ancient Mesopotamian civilization that existed as a city-state from the 21st century BC to the 14th century BC and eventually expanded into an empire from the 14th century BC t ...
n lenses such as the Nimrud lens. The ancient Roman
In modern historiography, ancient Rome is the Roman people, Roman civilisation from the founding of Rome, founding of the Italian city of Rome in the 8th century BC to the Fall of the Western Roman Empire, collapse of the Western Roman Em ...
s and Greeks
Greeks or Hellenes (; , ) are an ethnic group and nation native to Greece, Greek Cypriots, Cyprus, Greeks in Albania, southern Albania, Greeks in Turkey#History, Anatolia, parts of Greeks in Italy, Italy and Egyptian Greeks, Egypt, and to a l ...
filled glass spheres with water to make lenses. These practical developments were followed by the development of theories of light and vision by ancient Greek and Indian philosophers, and the development of geometrical optics in the Greco-Roman world
The Greco-Roman world , also Greco-Roman civilization, Greco-Roman culture or Greco-Latin culture (spelled Gr├”co-Roman or Graeco-Roman in British English), as understood by modern scholars and writers, includes the geographical regions and co ...
. The word ''optics'' comes from the ancient Greek
Ancient Greek (, ; ) includes the forms of the Greek language used in ancient Greece and the classical antiquity, ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Greek ...
word , .
Greek philosophy on optics broke down into two opposing theories on how vision worked, the intromission theory and the emission theory. The intromission approach saw vision as coming from objects casting off copies of themselves (called eidola) that were captured by the eye. With many propagators including Democritus
Democritus (, ; , ''D─ōm├│kritos'', meaning "chosen of the people"; ŌĆō ) was an Ancient Greece, Ancient Greek Pre-Socratic philosophy, pre-Socratic philosopher from Abdera, Thrace, Abdera, primarily remembered today for his formulation of an ...
, Epicurus
Epicurus (, ; ; 341ŌĆō270 BC) was an Greek philosophy, ancient Greek philosopher who founded Epicureanism, a highly influential school of philosophy that asserted that philosophy's purpose is to attain as well as to help others attain tranqui ...
, Aristotle
Aristotle (; 384ŌĆō322 BC) was an Ancient Greek philosophy, Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, a ...
and their followers, this theory seems to have some contact with modern theories of what vision really is, but it remained only speculation lacking any experimental foundation.
Plato
Plato ( ; Greek language, Greek: , ; born BC, died 348/347 BC) was an ancient Greek philosopher of the Classical Greece, Classical period who is considered a foundational thinker in Western philosophy and an innovator of the writte ...
first articulated the emission theory, the idea that visual perception
Visual perception is the ability to detect light and use it to form an image of the surrounding Biophysical environment, environment. Photodetection without image formation is classified as ''light sensing''. In most vertebrates, visual percept ...
is accomplished by rays emitted by the eyes. He also commented on the parity reversal of mirrors in '' Timaeus''. Some hundred years later, Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
(4thŌĆō3rd century BC) wrote a treatise entitled ''Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
'' where he linked vision to geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, creating ''geometrical optics''. He based his work on Plato's emission theory wherein he described the mathematical rules of perspective and described the effects of refraction
In physics, refraction is the redirection of a wave as it passes from one transmission medium, medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commo ...
qualitatively, although he questioned that a beam of light from the eye could instantaneously light up the stars every time someone blinked. Euclid stated the principle of shortest trajectory of light, and considered multiple reflections on flat and spherical mirrors.
Ptolemy
Claudius Ptolemy (; , ; ; ŌĆō 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzant ...
, in his treatise ''Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
'', held an extramission-intromission theory of vision: the rays (or flux) from the eye formed a cone, the vertex being within the eye, and the base defining the visual field. The rays were sensitive, and conveyed information back to the observer's intellect about the distance and orientation of surfaces. He summarized much of Euclid and went on to describe a way to measure the angle of refraction, though he failed to notice the empirical relationship between it and the angle of incidence. Plutarch
Plutarch (; , ''Plo├║tarchos'', ; ŌĆō 120s) was a Greek Middle Platonist philosopher, historian, biographer, essayist, and priest at the Temple of Apollo (Delphi), Temple of Apollo in Delphi. He is known primarily for his ''Parallel Lives'', ...
(1stŌĆō2nd century AD) described multiple reflections on spherical mirrors and discussed the creation of magnified and reduced images, both real and imaginary, including the case of chirality of the images.
 During the
During the Middle Ages
In the history of Europe, the Middle Ages or medieval period lasted approximately from the 5th to the late 15th centuries, similarly to the post-classical period of global history. It began with the fall of the Western Roman Empire and ...
, Greek ideas about optics were resurrected and extended by writers in the Muslim world
The terms Islamic world and Muslim world commonly refer to the Islamic community, which is also known as the Ummah. This consists of all those who adhere to the religious beliefs, politics, and laws of Islam or to societies in which Islam is ...
. One of the earliest of these was Al-Kindi (ŌĆō873) who wrote on the merits of Aristotelian and Euclidean ideas of optics, favouring the emission theory since it could better quantify optical phenomena. In 984, the Persia
Iran, officially the Islamic Republic of Iran (IRI) and also known as Persia, is a country in West Asia. It borders Iraq to the west, Turkey, Azerbaijan, and Armenia to the northwest, the Caspian Sea to the north, Turkmenistan to the nort ...
n mathematician Ibn Sahl wrote the treatise "On burning mirrors and lenses", correctly describing a law of refraction equivalent to Snell's law. He used this law to compute optimum shapes for lenses and curved mirrors. In the early 11th century, Alhazen (Ibn al-Haytham) wrote the '' Book of Optics'' (''Kitab al-manazir'') in which he explored reflection and refraction and proposed a new system for explaining vision and light based on observation and experiment. He rejected the "emission theory" of Ptolemaic optics with its rays being emitted by the eye, and instead put forward the idea that light reflected in all directions in straight lines from all points of the objects being viewed and then entered the eye, although he was unable to correctly explain how the eye captured the rays. Alhazen's work was largely ignored in the Arabic world but it was anonymously translated into Latin around 1200 A.D. and further summarised and expanded on by the Polish monk Witelo making it a standard text on optics in Europe for the next 400 years.
In the 13th century in medieval Europe, English bishop Robert Grosseteste wrote on a wide range of scientific topics, and discussed light from four different perspectives: an epistemology
Epistemology is the branch of philosophy that examines the nature, origin, and limits of knowledge. Also called "the theory of knowledge", it explores different types of knowledge, such as propositional knowledge about facts, practical knowle ...
of light, a metaphysics
Metaphysics is the branch of philosophy that examines the basic structure of reality. It is traditionally seen as the study of mind-independent features of the world, but some theorists view it as an inquiry into the conceptual framework of ...
or cosmogony of light, an etiology or physics of light, and a theology
Theology is the study of religious belief from a Religion, religious perspective, with a focus on the nature of divinity. It is taught as an Discipline (academia), academic discipline, typically in universities and seminaries. It occupies itse ...
of light, basing it on the works of Aristotle and Platonism. Grosseteste's most famous disciple, Roger Bacon
Roger Bacon (; or ', also '' Rogerus''; ), also known by the Scholastic accolades, scholastic accolade ''Doctor Mirabilis'', was a medieval English polymath, philosopher, scientist, theologian and Franciscans, Franciscan friar who placed co ...
, wrote works citing a wide range of recently translated optical and philosophical works, including those of Alhazen, Aristotle, Avicenna
Ibn Sina ( ŌĆō 22 June 1037), commonly known in the West as Avicenna ( ), was a preeminent philosopher and physician of the Muslim world, flourishing during the Islamic Golden Age, serving in the courts of various Iranian peoples, Iranian ...
, Averroes, Euclid, al-Kindi, Ptolemy, Tideus, and Constantine the African. Bacon was able to use parts of glass spheres as magnifying glasses to demonstrate that light reflects from objects rather than being released from them.
The first wearable eyeglasses were invented in Italy around 1286.
This was the start of the optical industry of grinding and polishing lenses for these "spectacles", first in Venice and Florence in the thirteenth century, and later in the spectacle making centres in both the Netherlands and Germany. Spectacle makers created improved types of lenses for the correction of vision based more on empirical knowledge gained from observing the effects of the lenses rather than using the rudimentary optical theory of the day (theory which for the most part could not even adequately explain how spectacles worked). This practical development, mastery, and experimentation with lenses led directly to the invention of the compound optical microscope around 1595, and the refracting telescope
A refracting telescope (also called a refractor) is a type of optical telescope that uses a lens (optics), lens as its objective (optics), objective to form an image (also referred to a dioptrics, dioptric telescope). The refracting telescope d ...
in 1608, both of which appeared in the spectacle making centres in the Netherlands.
In the early 17th century, Johannes Kepler
Johannes Kepler (27 December 1571 ŌĆō 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...
expanded on geometric optics in his writings, covering lenses, reflection by flat and curved mirrors, the principles of pinhole cameras, inverse-square law governing the intensity of light, and the optical explanations of astronomical phenomena such as lunar and solar eclipse
A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby obscuring the view of the Sun from a small part of Earth, totally or partially. Such an alignment occurs approximately every six months, during the eclipse season i ...
s and astronomical parallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different sightline, lines of sight and is measured by the angle or half-angle of inclination between those two lines. Due to perspective (graphica ...
. He was also able to correctly deduce the role of the retina as the actual organ that recorded images, finally being able to scientifically quantify the effects of different types of lenses that spectacle makers had been observing over the previous 300 years. After the invention of the telescope, Kepler set out the theoretical basis on how they worked and described an improved version, known as the '' Keplerian telescope'', using two convex lenses to produce higher magnification.
Optical theory progressed in the mid-17th century with treatises written by philosopher Ren├® Descartes
Ren├® Descartes ( , ; ; 31 March 1596 ŌĆō 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramou ...
, which explained a variety of optical phenomena including reflection and refraction by assuming that light was emitted by objects which produced it. This differed substantively from the ancient Greek emission theory. In the late 1660s and early 1670s, Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
expanded Descartes's ideas into a corpuscle theory of light, famously determining that white light was a mix of colours that can be separated into its component parts with a prism. In 1690, Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 ŌĆō 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution ...
proposed a wave theory for light based on suggestions that had been made by Robert Hooke in 1664. Hooke himself publicly criticised Newton's theories of light and the feud between the two lasted until Hooke's death. In 1704, Newton published ''Opticks
''Opticks: or, A Treatise of the Reflexions, Refractions, Inflexions and Colours of Light'' is a collection of three books by Isaac Newton that was published in English language, English in 1704 (a scholarly Latin translation appeared in 1706). ...
'' and, at the time, partly because of his success in other areas of physics, he was generally considered to be the victor in the debate over the nature of light.
Newtonian optics was generally accepted until the early 19th century when Thomas Young and Augustin-Jean Fresnel conducted experiments on the interference of light that firmly established light's wave nature. Young's famous double slit experiment showed that light followed the superposition principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So th ...
, which is a wave-like property not predicted by Newton's corpuscle theory. This work led to a theory of diffraction for light and opened an entire area of study in physical optics. Wave optics was successfully unified with electromagnetic theory by James Clerk Maxwell
James Clerk Maxwell (13 June 1831 ŌĆō 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism an ...
in the 1860s.
The next development in optical theory came in 1899 when Max Planck
Max Karl Ernst Ludwig Planck (; ; 23 April 1858 ŌĆō 4 October 1947) was a German Theoretical physics, theoretical physicist whose discovery of energy quantum, quanta won him the Nobel Prize in Physics in 1918.
Planck made many substantial con ...
correctly modelled blackbody radiation by assuming that the exchange of energy between light and matter only occurred in discrete amounts he called ''quanta''. In 1905, Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His massŌĆōenergy equivalence f ...
published the theory of the photoelectric effect that firmly established the quantization of light itself. In 1913, Niels Bohr
Niels Henrik David Bohr (, ; ; 7 October 1885 ŌĆō 18 November 1962) was a Danish theoretical physicist who made foundational contributions to understanding atomic structure and old quantum theory, quantum theory, for which he received the No ...
showed that atoms could only emit discrete amounts of energy, thus explaining the discrete lines seen in emission and absorption spectra. The understanding of the interaction between light and matter that followed from these developments not only formed the basis of quantum optics but also was crucial for the development of quantum mechanics as a whole. The ultimate culmination, the theory of quantum electrodynamics
In particle physics, quantum electrodynamics (QED) is the Theory of relativity, relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quant ...
, explains all optics and electromagnetic processes in general as the result of the exchange of real and virtual photons. Quantum optics gained practical importance with the inventions of the maser in 1953 and of the laser in 1960.
Following the work of Paul Dirac in quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct phy ...
, George Sudarshan, Roy J. Glauber, and Leonard Mandel applied quantum theory to the electromagnetic field in the 1950s and 1960s to gain a more detailed understanding of photodetection and the statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
of light.
Classical optics
 Classical optics is divided into two main branches: geometrical (or ray) optics and physical (or wave) optics. In geometrical optics, light is considered to travel in straight lines, while in physical optics, light is considered as an electromagnetic wave.
Geometrical optics can be viewed as an approximation of physical optics that applies when the wavelength of the light used is much smaller than the size of the optical elements in the system being modelled.
Classical optics is divided into two main branches: geometrical (or ray) optics and physical (or wave) optics. In geometrical optics, light is considered to travel in straight lines, while in physical optics, light is considered as an electromagnetic wave.
Geometrical optics can be viewed as an approximation of physical optics that applies when the wavelength of the light used is much smaller than the size of the optical elements in the system being modelled.
Geometrical optics
refractive index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refrac ...
of the second material.
The laws of reflection and refraction can be derived from Fermat's principle which states that ''the path taken between two points by a ray of light is the path that can be traversed in the least time.''
Approximations
Geometric optics is often simplified by making the paraxial approximation, or "small angle approximation". The mathematical behaviour then becomes linear, allowing optical components and systems to be described by simple matrices. This leads to the techniques ofGaussian optics
Gaussian optics is a technique in geometrical optics that describes the behaviour of light rays in optical systems by using the paraxial approximation, in which only rays which make small angles with the optical axis of the system are considered. ...
and ''paraxial ray tracing'', which are used to find basic properties of optical systems, such as approximate image
An image or picture is a visual representation. An image can be Two-dimensional space, two-dimensional, such as a drawing, painting, or photograph, or Three-dimensional space, three-dimensional, such as a carving or sculpture. Images may be di ...
and object positions and magnifications.
Reflections
surface normal
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the ...
, a line perpendicular to the surface at the point where the ray hits. The incident and reflected rays and the normal lie in a single plane, and the angle between the reflected ray and the surface normal is the same as that between the incident ray and the normal. This is known as the Law of Reflection.
For flat mirrors, the law of reflection implies that images of objects are upright and the same distance behind the mirror as the objects are in front of the mirror. The image size is the same as the object size. The law also implies that mirror image
A mirror image (in a plane mirror) is a reflection (physics), reflected duplication of an object that appears almost identical, but is reversed in the direction perpendicular to the mirror surface. As an optical phenomenon, optical effect, it r ...
s are parity inverted, which we perceive as a left-right inversion. Images formed from reflection in two (or any even number of) mirrors are not parity inverted. Corner reflectors produce reflected rays that travel back in the direction from which the incident rays came. This is called retroreflection.
Mirrors with curved surfaces can be modelled by ray tracing and using the law of reflection at each point on the surface. For mirrors with parabolic surfaces, parallel rays incident on the mirror produce reflected rays that converge at a common focus. Other curved surfaces may also focus light, but with aberrations due to the diverging shape causing the focus to be smeared out in space. In particular, spherical mirrors exhibit spherical aberration. Curved mirrors can form images with a magnification greater than or less than one, and the magnification can be negative, indicating that the image is inverted. An upright image formed by reflection in a mirror is always virtual, while an inverted image is real and can be projected onto a screen.
Refractions
=Lenses
= A device that produces converging or diverging light rays due to refraction is known as a ''lens''. Lenses are characterized by theirfocal length
The focal length of an Optics, optical system is a measure of how strongly the system converges or diverges light; it is the Multiplicative inverse, inverse of the system's optical power. A positive focal length indicates that a system Converge ...
: a converging lens has positive focal length, while a diverging lens has negative focal length. Smaller focal length indicates that the lens has a stronger converging or diverging effect. The focal length of a simple lens in air is given by the lensmaker's equation.
Ray tracing can be used to show how images are formed by a lens. For a thin lens in air, the location of the image is given by the simple equation
where is the distance from the object to the lens, is the distance from the lens to the image, and is the focal length of the lens. In the sign convention used here, the object and image distances are positive if the object and image are on opposite sides of the lens.
Physical optics
In physical optics, light is considered to propagate as waves. This model predicts phenomena such as interference and diffraction, which are not explained by geometric optics. Thespeed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
waves in air is approximately 3.0├Ś108 m/s (exactly 299,792,458 m/s in vacuum). The wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.
In other words, it is the distance between consecutive corresponding points of the same ''phase (waves ...
of visible light waves varies between 400 and 700 nm, but the term "light" is also often applied to infrared (0.7ŌĆō300 ╬╝m) and ultraviolet radiation (10ŌĆō400 nm).
The wave model can be used to make predictions about how an optical system will behave without requiring an explanation of what is "waving" in what medium. Until the middle of the 19th century, most physicists believed in an "ethereal" medium in which the light disturbance propagated. The existence of electromagnetic waves was predicted in 1865 by Maxwell's equations
Maxwell's equations, or MaxwellŌĆōHeaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, Electrical network, electr ...
. These waves propagate at the speed of light and have varying electric and magnetic fields which are orthogonal to one another, and also to the direction of propagation of the waves. Light waves are now generally treated as electromagnetic waves except when quantum mechanical effects have to be considered.
Modelling and design of optical systems using physical optics
Many simplified approximations are available for analysing and designing optical systems. Most of these use a single scalar quantity to represent the electric field of the light wave, rather than using a vector model with orthogonal electric and magnetic vectors.M. Born and E. Wolf (1999). ''Principle of Optics''. Cambridge: Cambridge University Press. . The HuygensŌĆōFresnel equation is one such model. This was derived empirically by Fresnel in 1815, based on Huygens' hypothesis that each point on a wavefront generates a secondary spherical wavefront, which Fresnel combined with the principle of superposition of waves. The Kirchhoff diffraction equation, which is derived using Maxwell's equations, puts the Huygens-Fresnel equation on a firmer physical foundation. Examples of the application of HuygensŌĆōFresnel principle can be found in the articles on diffraction and Fraunhofer diffraction. More rigorous models, involving the modelling of both electric and magnetic fields of the light wave, are required when dealing with materials whose electric and magnetic properties affect the interaction of light with the material. For instance, the behaviour of a light wave interacting with a metal surface is quite different from what happens when it interacts with a dielectric material. A vector model must also be used to model polarised light. Numerical modeling techniques such as the finite element method, the boundary element method and the transmission-line matrix method can be used to model the propagation of light in systems which cannot be solved analytically. Such models are computationally demanding and are normally only used to solve small-scale problems that require accuracy beyond that which can be achieved with analytical solutions. All of the results from geometrical optics can be recovered using the techniques of Fourier optics which apply many of the same mathematical and analytical techniques used in acoustic engineering andsignal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomograph ...
.
Gaussian beam propagation is a simple paraxial physical optics model for the propagation of coherent radiation such as laser beams. This technique partially accounts for diffraction, allowing accurate calculations of the rate at which a laser beam expands with distance, and the minimum size to which the beam can be focused. Gaussian beam propagation thus bridges the gap between geometric and physical optics.
Superposition and interference
In the absence of nonlinear effects, the superposition principle can be used to predict the shape of interacting waveforms through the simple addition of the disturbances. This interaction of waves to produce a resulting pattern is generally termed "interference" and can result in a variety of outcomes. If two waves of the same wavelength and frequency are ''in phase'', both the wave crests and wave troughs align. This results in constructive interference and an increase in the amplitude of the wave, which for light is associated with a brightening of the waveform in that location. Alternatively, if the two waves of the same wavelength and frequency are out of phase, then the wave crests will align with wave troughs and vice versa. This results in destructive interference and a decrease in the amplitude of the wave, which for light is associated with a dimming of the waveform at that location. See below for an illustration of this effect. Since the HuygensŌĆōFresnel principle states that every point of a wavefront is associated with the production of a new disturbance, it is possible for a wavefront to interfere with itself constructively or destructively at different locations producing bright and dark fringes in regular and predictable patterns. Interferometry is the science of measuring these patterns, usually as a means of making precise determinations of distances or angular resolutions. The Michelson interferometer was a famous instrument which used interference effects to accurately measure the speed of light.
The appearance of thin films and coatings is directly affected by interference effects. Antireflective coatings use destructive interference to reduce the reflectivity of the surfaces they coat, and can be used to minimise glare and unwanted reflections. The simplest case is a single layer with a thickness of one-fourth the wavelength of incident light. The reflected wave from the top of the film and the reflected wave from the film/material interface are then exactly 180┬░ out of phase, causing destructive interference. The waves are only exactly out of phase for one wavelength, which would typically be chosen to be near the centre of the visible spectrum, around 550 nm. More complex designs using multiple layers can achieve low reflectivity over a broad band, or extremely low reflectivity at a single wavelength.
Constructive interference in thin films can create a strong reflection of light in a range of wavelengths, which can be narrow or broad depending on the design of the coating. These films are used to make dielectric mirrors, interference filters, heat reflectors, and filters for colour separation in colour television cameras. This interference effect is also what causes the colourful rainbow patterns seen in oil slicks.
Since the HuygensŌĆōFresnel principle states that every point of a wavefront is associated with the production of a new disturbance, it is possible for a wavefront to interfere with itself constructively or destructively at different locations producing bright and dark fringes in regular and predictable patterns. Interferometry is the science of measuring these patterns, usually as a means of making precise determinations of distances or angular resolutions. The Michelson interferometer was a famous instrument which used interference effects to accurately measure the speed of light.
The appearance of thin films and coatings is directly affected by interference effects. Antireflective coatings use destructive interference to reduce the reflectivity of the surfaces they coat, and can be used to minimise glare and unwanted reflections. The simplest case is a single layer with a thickness of one-fourth the wavelength of incident light. The reflected wave from the top of the film and the reflected wave from the film/material interface are then exactly 180┬░ out of phase, causing destructive interference. The waves are only exactly out of phase for one wavelength, which would typically be chosen to be near the centre of the visible spectrum, around 550 nm. More complex designs using multiple layers can achieve low reflectivity over a broad band, or extremely low reflectivity at a single wavelength.
Constructive interference in thin films can create a strong reflection of light in a range of wavelengths, which can be narrow or broad depending on the design of the coating. These films are used to make dielectric mirrors, interference filters, heat reflectors, and filters for colour separation in colour television cameras. This interference effect is also what causes the colourful rainbow patterns seen in oil slicks.
Diffraction and optical resolution
Francesco Maria Grimaldi
Francesco Maria Grimaldi (2 April 1618 ŌĆō 28 December 1663) was an Italian Jesuit priest, mathematician and physicist who taught at the Jesuit college in Bologna. He was born in Bologna to Paride Grimaldi and Anna Cattani.
Work
Between 164 ...
, who also coined the term from the Latin . Later that century, Robert Hooke and Isaac Newton also described phenomena now known to be diffraction in Newton's rings while James Gregory recorded his observations of diffraction patterns from bird feathers.
The first physical optics model of diffraction that relied on the HuygensŌĆōFresnel principle was developed in 1803 by Thomas Young in his interference experiments with the interference patterns of two closely spaced slits. Young showed that his results could only be explained if the two slits acted as two unique sources of waves rather than corpuscles. In 1815 and 1818, Augustin-Jean Fresnel firmly established the mathematics of how wave interference can account for diffraction.
The simplest physical models of diffraction use equations that describe the angular separation of light and dark fringes due to light of a particular wavelength (). In general, the equation takes the form
where is the separation between two wavefront sources (in the case of Young's experiments, it was two slits), is the angular separation between the central fringe and the order fringe, where the central maximum is .
This equation is modified slightly to take into account a variety of situations such as diffraction through a single gap, diffraction through multiple slits, or diffraction through a diffraction grating
In optics, a diffraction grating is an optical grating with a periodic structure that diffraction, diffracts light, or another type of electromagnetic radiation, into several beams traveling in different directions (i.e., different diffractio ...
that contains a large number of slits at equal spacing. More complicated models of diffraction require working with the mathematics of Fresnel or Fraunhofer diffraction.
X-ray diffraction
X-ray diffraction is a generic term for phenomena associated with changes in the direction of X-ray beams due to interactions with the electrons around atoms. It occurs due to elastic scattering, when there is no change in the energy of the waves. ...
makes use of the fact that atoms in a crystal have regular spacing at distances that are on the order of one angstrom. To see diffraction patterns, x-rays with similar wavelengths to that spacing are passed through the crystal. Since crystals are three-dimensional objects rather than two-dimensional gratings, the associated diffraction pattern varies in two directions according to Bragg reflection, with the associated bright spots occurring in unique patterns and being twice the spacing between atoms.
Diffraction effects limit the ability of an optical detector to optically resolve separate light sources. In general, light that is passing through an aperture will experience diffraction and the best images that can be created (as described in diffraction-limited optics) appear as a central spot with surrounding bright rings, separated by dark nulls; this pattern is known as an Airy pattern, and the central bright lobe as an Airy disk. The size of such a disk is given by where is the angular resolution, is the wavelength of the light, and is the diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions a ...
of the lens aperture. If the angular separation of the two points is significantly less than the Airy disk angular radius, then the two points cannot be resolved in the image, but if their angular separation is much greater than this, distinct images of the two points are formed and they can therefore be resolved. Rayleigh defined the somewhat arbitrary " Rayleigh criterion" that two points whose angular separation is equal to the Airy disk radius (measured to first null, that is, to the first place where no light is seen) can be considered to be resolved. It can be seen that the greater the diameter of the lens or its aperture, the finer the resolution. Interferometry, with its ability to mimic extremely large baseline apertures, allows for the greatest angular resolution possible.
For astronomical imaging, the atmosphere prevents optimal resolution from being achieved in the visible spectrum due to the atmospheric scattering
In physics, scattering is a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities (including particles and radiat ...
and dispersion which cause stars to twinkle. Astronomers refer to this effect as the quality of astronomical seeing. Techniques known as adaptive optics have been used to eliminate the atmospheric disruption of images and achieve results that approach the diffraction limit.
Dispersion and scattering
 Refractive processes take place in the physical optics limit, where the wavelength of light is similar to other distances, as a kind of scattering. The simplest type of scattering is Thomson scattering which occurs when electromagnetic waves are deflected by single particles. In the limit of Thomson scattering, in which the wavelike nature of light is evident, light is dispersed independent of the frequency, in contrast to Compton scattering which is frequency-dependent and strictly a quantum mechanical process, involving the nature of light as particles. In a statistical sense, elastic scattering of light by numerous particles much smaller than the wavelength of the light is a process known as Rayleigh scattering while the similar process for scattering by particles that are similar or larger in wavelength is known as Mie scattering with the Tyndall effect being a commonly observed result. A small proportion of light scattering from atoms or molecules may undergo Raman scattering, wherein the frequency changes due to excitation of the atoms and molecules. Brillouin scattering occurs when the frequency of light changes due to local changes with time and movements of a dense material.
Dispersion occurs when different frequencies of light have different phase velocities, due either to material properties (''material dispersion'') or to the geometry of an
Refractive processes take place in the physical optics limit, where the wavelength of light is similar to other distances, as a kind of scattering. The simplest type of scattering is Thomson scattering which occurs when electromagnetic waves are deflected by single particles. In the limit of Thomson scattering, in which the wavelike nature of light is evident, light is dispersed independent of the frequency, in contrast to Compton scattering which is frequency-dependent and strictly a quantum mechanical process, involving the nature of light as particles. In a statistical sense, elastic scattering of light by numerous particles much smaller than the wavelength of the light is a process known as Rayleigh scattering while the similar process for scattering by particles that are similar or larger in wavelength is known as Mie scattering with the Tyndall effect being a commonly observed result. A small proportion of light scattering from atoms or molecules may undergo Raman scattering, wherein the frequency changes due to excitation of the atoms and molecules. Brillouin scattering occurs when the frequency of light changes due to local changes with time and movements of a dense material.
Dispersion occurs when different frequencies of light have different phase velocities, due either to material properties (''material dispersion'') or to the geometry of an optical waveguide
An optical waveguide is a physical structure that guides electromagnetic waves in the optical spectrum. Common types of optical waveguides include optical fiber waveguides, transparent dielectric waveguides made of plastic and glass, liquid ligh ...
(''waveguide dispersion''). The most familiar form of dispersion is a decrease in index of refraction with increasing wavelength, which is seen in most transparent materials. This is called "normal dispersion". It occurs in all dielectric materials, in wavelength ranges where the material does not absorb light. In wavelength ranges where a medium has significant absorption, the index of refraction can increase with wavelength. This is called "anomalous dispersion".
The separation of colours by a prism is an example of normal dispersion. At the surfaces of the prism, Snell's law predicts that light incident at an angle to the normal will be refracted at an angle . Thus, blue light, with its higher refractive index, is bent more strongly than red light, resulting in the well-known rainbow pattern.
 Material dispersion is often characterised by the Abbe number, which gives a simple measure of dispersion based on the index of refraction at three specific wavelengths. Waveguide dispersion is dependent on the propagation constant. Both kinds of dispersion cause changes in the group characteristics of the wave, the features of the wave packet that change with the same frequency as the amplitude of the electromagnetic wave. "Group velocity dispersion" manifests as a spreading-out of the signal "envelope" of the radiation and can be quantified with a group dispersion delay parameter:
where is the group velocity. For a uniform medium, the group velocity is
where is the index of refraction and is the speed of light in a vacuum. This gives a simpler form for the dispersion delay parameter:
If is less than zero, the medium is said to have ''positive dispersion'' or normal dispersion. If is greater than zero, the medium has ''negative dispersion''. If a light pulse is propagated through a normally dispersive medium, the result is the higher frequency components slow down more than the lower frequency components. The pulse therefore becomes ''positively chirped'', or ''up-chirped'', increasing in frequency with time. This causes the spectrum coming out of a prism to appear with red light the least refracted and blue/violet light the most refracted. Conversely, if a pulse travels through an anomalously (negatively) dispersive medium, high-frequency components travel faster than the lower ones, and the pulse becomes ''negatively chirped'', or ''down-chirped'', decreasing in frequency with time.
The result of group velocity dispersion, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on optical fibres, since if dispersion is too high, a group of pulses representing information will each spread in time and merge, making it impossible to extract the signal.
Material dispersion is often characterised by the Abbe number, which gives a simple measure of dispersion based on the index of refraction at three specific wavelengths. Waveguide dispersion is dependent on the propagation constant. Both kinds of dispersion cause changes in the group characteristics of the wave, the features of the wave packet that change with the same frequency as the amplitude of the electromagnetic wave. "Group velocity dispersion" manifests as a spreading-out of the signal "envelope" of the radiation and can be quantified with a group dispersion delay parameter:
where is the group velocity. For a uniform medium, the group velocity is
where is the index of refraction and is the speed of light in a vacuum. This gives a simpler form for the dispersion delay parameter:
If is less than zero, the medium is said to have ''positive dispersion'' or normal dispersion. If is greater than zero, the medium has ''negative dispersion''. If a light pulse is propagated through a normally dispersive medium, the result is the higher frequency components slow down more than the lower frequency components. The pulse therefore becomes ''positively chirped'', or ''up-chirped'', increasing in frequency with time. This causes the spectrum coming out of a prism to appear with red light the least refracted and blue/violet light the most refracted. Conversely, if a pulse travels through an anomalously (negatively) dispersive medium, high-frequency components travel faster than the lower ones, and the pulse becomes ''negatively chirped'', or ''down-chirped'', decreasing in frequency with time.
The result of group velocity dispersion, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on optical fibres, since if dispersion is too high, a group of pulses representing information will each spread in time and merge, making it impossible to extract the signal.
Polarisation
Polarisation is a general property of waves that describes the orientation of their oscillations. For transverse waves such as many electromagnetic waves, it describes the orientation of the oscillations in the plane perpendicular to the wave's direction of travel. The oscillations may be oriented in a single direction ( linear polarisation), or the oscillation direction may rotate as the wave travels ( circular or elliptical polarisation). Circularly polarised waves can rotate rightward or leftward in the direction of travel, and which of those two rotations is present in a wave is called the wave's chirality. The typical way to consider polarisation is to keep track of the orientation of the electric field vector as the electromagnetic wave propagates. The electric field vector of a plane wave may be arbitrarily divided into two perpendicularcomponents
Component may refer to:
In engineering, science, and technology Generic systems
*System components, an entity with discrete structure, such as an assembly or software module, within a system considered at a particular level of analysis
* Lumped e ...
labeled and (with indicating the direction of travel). The shape traced out in the x-y plane by the electric field vector is a Lissajous figure that describes the ''polarisation state''. The following figures show some examples of the evolution of the electric field vector (blue), with time (the vertical axes), at a particular point in space, along with its and components (red/left and green/right), and the path traced by the vector in the plane (purple): The same evolution would occur when looking at the electric field at a particular time while evolving the point in space, along the direction opposite to propagation.
ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
in the plane (the ''polarisation ellipse''). This is shown in the above figure on the right. Detailed mathematics of polarisation is done using Jones calculus and is characterised by the Stokes parameters.
=Changing polarisation
= Media that have different indexes of refraction for different polarisation modes are called '' birefringent''. Well known manifestations of this effect appear in optical wave plates/retarders (linear modes) and in Faraday rotation/ optical rotation (circular modes). If the path length in the birefringent medium is sufficient, plane waves will exit the material with a significantly different propagation direction, due to refraction. For example, this is the case with macroscopic crystals ofcalcite
Calcite is a Carbonate minerals, carbonate mineral and the most stable Polymorphism (materials science), polymorph of calcium carbonate (CaCO3). It is a very common mineral, particularly as a component of limestone. Calcite defines hardness 3 on ...
, which present the viewer with two offset, orthogonally polarised images of whatever is viewed through them. It was this effect that provided the first discovery of polarisation, by Erasmus Bartholinus in 1669. In addition, the phase shift, and thus the change in polarisation state, is usually frequency dependent, which, in combination with dichroism
In optics, a dichroic material is either one which causes visible light to be split up into distinct beams of different wavelengths (colours) (not to be confused with Dispersion (optics), dispersion), or one in which light rays having different P ...
, often gives rise to bright colours and rainbow-like effects. In mineralogy
Mineralogy is a subject of geology specializing in the scientific study of the chemistry, crystal structure, and physical (including optical mineralogy, optical) properties of minerals and mineralized artifact (archaeology), artifacts. Specific s ...
, such properties, known as pleochroism, are frequently exploited for the purpose of identifying minerals using polarisation microscopes. Additionally, many plastics that are not normally birefringent will become so when subject to mechanical stress, a phenomenon which is the basis of photoelasticity. Non-birefringent methods, to rotate the linear polarisation of light beams, include the use of prismatic polarisation rotators which use total internal reflection in a prism set designed for efficient collinear transmission.
=Natural light
= Most sources of electromagnetic radiation contain a large number of atoms or molecules that emit light. The orientation of the electric fields produced by these emitters may not be
Most sources of electromagnetic radiation contain a large number of atoms or molecules that emit light. The orientation of the electric fields produced by these emitters may not be correlated
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistic ...
, in which case the light is said to be ''unpolarised''. If there is partial correlation between the emitters, the light is ''partially polarised''. If the polarisation is consistent across the spectrum of the source, partially polarised light can be described as a superposition of a completely unpolarised component, and a completely polarised one. One may then describe the light in terms of the degree of polarisation, and the parameters of the polarisation ellipse.
Light reflected by shiny transparent materials is partly or fully polarised, except when the light is normal (perpendicular) to the surface. It was this effect that allowed the mathematician ├ētienne-Louis Malus to make the measurements that allowed for his development of the first mathematical models for polarised light. Polarisation occurs when light is scattered in the atmosphere
An atmosphere () is a layer of gases that envelop an astronomical object, held in place by the gravity of the object. A planet retains an atmosphere when the gravity is great and the temperature of the atmosphere is low. A stellar atmosph ...
. The scattered light produces the brightness and colour in clear skies. This partial polarisation of scattered light can be taken advantage of using polarising filters to darken the sky in photographs. Optical polarisation is principally of importance in chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
due to circular dichroism
Circular dichroism (CD) is dichroism involving circular polarization, circularly polarized light, i.e., the differential Absorption (electromagnetic radiation), absorption of left- and right-handed light. Left-hand circular (LHC) and right-hand ci ...
and optical rotation (''circular birefringence'') exhibited by optically active ( chiral) molecules
A molecule is a group of two or more atoms that are held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions that satisfy this criterion. In quantum physics, organic chemistry ...
.
Modern optics
''Modern optics'' encompasses the areas of optical science and engineering that became popular in the 20th century. These areas of optical science typically relate to the electromagnetic or quantum properties of light but do include other topics. A major subfield of modern optics, quantum optics, deals with specifically quantum mechanical properties of light. Quantum optics is not just theoretical; some modern devices, such as lasers, have principles of operation that depend on quantum mechanics. Light detectors, such as photomultipliers and channeltrons, respond to individual photons. Electronicimage sensor An image sensor or imager is a sensor that detects and conveys information used to form an image. It does so by converting the variable attenuation of light waves (as they refraction, pass through or reflection (physics), reflect off objects) into s ...
s, such as CCDs, exhibit shot noise
Shot noise or Poisson noise is a type of noise which can be modeled by a Poisson process.
In electronics shot noise originates from the discrete nature of electric charge. Shot noise also occurs in photon counting in optical devices, where s ...
corresponding to the statistics of individual photon events. Light-emitting diode
A light-emitting diode (LED) is a semiconductor device that emits light when current flows through it. Electrons in the semiconductor recombine with electron holes, releasing energy in the form of photons. The color of the light (corre ...
s and photovoltaic cell
A solar cell, also known as a photovoltaic cell (PV cell), is an electronic device that converts the energy of light directly into electricity by means of the photovoltaic effect.
s, too, cannot be understood without quantum mechanics. In the study of these devices, quantum optics often overlaps with quantum electronics.
Specialty areas of optics research include the study of how light interacts with specific materials as in crystal optics and metamaterials. Other research focuses on the phenomenology of electromagnetic waves as in singular optics, non-imaging optics, non-linear optics, statistical optics, and radiometry
Radiometry is a set of techniques for measurement, measuring electromagnetic radiation, including visible light. Radiometric techniques in optics characterize the distribution of the radiation's power (physics), power in space, as opposed to phot ...
. Additionally, computer engineers have taken an interest in integrated optics, machine vision
Machine vision is the technology and methods used to provide image, imaging-based automation, automatic inspection and analysis for such applications as automatic inspection, process control, and robot guidance, usually in industry. Machine vision ...
, and photonic computing as possible components of the "next generation" of computers.
Today, the pure science of optics is called optical science or optical physics to distinguish it from applied optical sciences, which are referred to as optical engineering
Optical engineering is the field of engineering encompassing the physical phenomena and technologies associated with the generation, transmission, manipulation, detection, and utilization of light. Optical engineers use the science of optics to ...
. Prominent subfields of optical engineering include illumination engineering, photonics, and optoelectronics with practical applications like lens design, fabrication and testing of optical components
Fabrication may refer to:
* Manufacturing, specifically the crafting of individual parts as a solo product or as part of a larger combined product.
Processes in arts, crafts and manufacturing
*Semiconductor device fabrication, the process used t ...
, and image processing
An image or picture is a visual representation. An image can be two-dimensional, such as a drawing, painting, or photograph, or three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a pr ...
. Some of these fields overlap, with nebulous boundaries between the subjects' terms that mean slightly different things in different parts of the world and in different areas of industry. A professional community of researchers in nonlinear optics has developed in the last several decades due to advances in laser technology.
Lasers
 A laser is a device that emits light, a kind of electromagnetic radiation, through a process called '' stimulated emission''. The term ''laser'' is an
A laser is a device that emits light, a kind of electromagnetic radiation, through a process called '' stimulated emission''. The term ''laser'' is an acronym
An acronym is a type of abbreviation consisting of a phrase whose only pronounced elements are the initial letters or initial sounds of words inside that phrase. Acronyms are often spelled with the initial Letter (alphabet), letter of each wor ...
for . Laser light is usually spatially coherent, which means that the light either is emitted in a narrow, low-divergence beam, or can be converted into one with the help of optical components such as lenses. Because the microwave equivalent of the laser, the ''maser'', was developed first, devices that emit microwave and radio
Radio is the technology of communicating using radio waves. Radio waves are electromagnetic waves of frequency between 3 hertz (Hz) and 300 gigahertz (GHz). They are generated by an electronic device called a transmitter connec ...
frequencies are usually called ''masers''.
The first working laser was demonstrated on 16 May 1960 by Theodore Maiman
Theodore Harold Maiman (July 11, 1927 ŌĆō May 5, 2007) was an American engineer and physicist who is widely credited with the invention of the laser.Johnson, John Jr. (May 11, 2008). "Theodore H. Maiman, at age 32; scientist created the first L ...
at Hughes Research Laboratories. When first invented, they were called "a solution looking for a problem". Since then, lasers have become a multibillion-dollar industry, finding utility in thousands of highly varied applications. The first application of lasers visible in the daily lives of the general population was the supermarket barcode scanner, introduced in 1974. The laserdisc
LaserDisc (LD) is a home video format and the first commercial optical disc storage medium. It was developed by Philips, Pioneer Corporation, Pioneer, and the movie studio MCA Inc., MCA. The format was initially marketed in the United State ...
player, introduced in 1978, was the first successful consumer product to include a laser, but the compact disc
The compact disc (CD) is a Digital media, digital optical disc data storage format co-developed by Philips and Sony to store and play digital audio recordings. It employs the Compact Disc Digital Audio (CD-DA) standard and was capable of hol ...
player was the first laser-equipped device to become truly common in consumers' homes, beginning in 1982. These optical storage devices use a semiconductor laser less than a millimetre wide to scan the surface of the disc for data retrieval. Fibre-optic communication
Fiber-optic communication is a form of optical communication for transmitting information from one place to another by sending pulses of infrared or visible light through an optical fiber. The light is a form of carrier wave that is modul ...
relies on lasers to transmit large amounts of information at the speed of light. Other common applications of lasers include laser printers and laser pointer
A laser pointer or laser pen is a (typically battery-powered) handheld device that uses a laser diode to emit a narrow low-power visible laser beam (i.e. Coherence (physics), coherent light) to highlight something of interest with a small brigh ...
s. Lasers are used in medicine in areas such as bloodless surgery, laser eye surgery, and laser capture microdissection and in military applications such as missile defence systems, electro-optical countermeasures (EOCM), and lidar
Lidar (, also LIDAR, an acronym of "light detection and ranging" or "laser imaging, detection, and ranging") is a method for determining ranging, ranges by targeting an object or a surface with a laser and measuring the time for the reflected li ...
. Lasers are also used in holograms, bubblegrams, laser light shows, and laser hair removal.
KapitsaŌĆōDirac effect
The KapitsaŌĆōDirac effect causes beams of particles to diffract as the result of meeting a standing wave of light. Light can be used to position matter using various phenomena (see optical tweezers).Applications
Optics is part of everyday life. The ubiquity ofvisual system
The visual system is the physiological basis of visual perception (the ability to perception, detect and process light). The system detects, phototransduction, transduces and interprets information concerning light within the visible range to ...
s in biology indicates the central role optics plays as the science of one of the five senses. Many people benefit from eyeglasses or contact lenses, and optics are integral to the functioning of many consumer goods including cameras. Rainbows and mirages are examples of optical phenomena. Optical communication
Optical communication, also known as optical telecommunication, is communication at a distance using light to carry information. It can be performed visually or by using electronic devices. The earliest basic forms of optical communication date ...
provides the backbone for both the Internet
The Internet (or internet) is the Global network, global system of interconnected computer networks that uses the Internet protocol suite (TCP/IP) to communicate between networks and devices. It is a internetworking, network of networks ...
and modern telephony
Telephony ( ) is the field of technology involving the development, application, and deployment of telecommunications services for the purpose of electronic transmission of voice, fax, or data, between distant parties. The history of telephony is ...
.
Human eye
colour
Color (or colour in Commonwealth English; see spelling differences) is the visual perception based on the electromagnetic spectrum. Though color is not an inherent property of matter, color perception is related to an object's light absorp ...
and photopic vision. Cone cells are highly concentrated in the fovea and have a high visual acuity meaning that they are better at spatial resolution than rod cells. Since cone cells are not as sensitive to dim light as rod cells, most night vision
Night vision is the ability to see in low-light conditions, either naturally with scotopic vision or through a night-vision device. Night vision requires both sufficient spectral range and sufficient intensity range. Humans have poor night v ...
is limited to rod cells. Likewise, since cone cells are in the fovea, central vision (including the vision needed to do most reading, fine detail work such as sewing, or careful examination of objects) is done by cone cells.
Ciliary muscles around the lens allow the eye's focus to be adjusted. This process is known as accommodation. The near point and far point define the nearest and farthest distances from the eye at which an object can be brought into sharp focus. For a person with normal vision, the far point is located at infinity. The near point's location depends on how much the muscles can increase the curvature of the lens, and how inflexible the lens has become with age. Optometrists, ophthalmologist
Ophthalmology (, ) is the branch of medicine that deals with the diagnosis, treatment, and surgery of eye diseases and disorders.
An ophthalmologist is a physician who undergoes subspecialty training in medical and surgical eye care. Following a ...
s, and opticians usually consider an appropriate near point to be closer than normal reading distanceŌĆöapproximately 25 cm.
Defects in vision can be explained using optical principles. As people age, the lens becomes less flexible and the near point recedes from the eye, a condition known as presbyopia
Presbyopia is a physiological insufficiency of optical Accommodation (vertebrate eye), accommodation associated with the aging of the human eye, eye; it results in progressively worsening ability to focus clearly on close objects. Also known as ...
. Similarly, people suffering from hyperopia cannot decrease the focal length of their lens enough to allow for nearby objects to be imaged on their retina. Conversely, people who cannot increase the focal length of their lens enough to allow for distant objects to be imaged on the retina suffer from myopia and have a far point that is considerably closer than infinity. A condition known as astigmatism results when the cornea is not spherical but instead is more curved in one direction. This causes horizontally extended objects to be focused on different parts of the retina than vertically extended objects, and results in distorted images.
All of these conditions can be corrected using corrective lenses. For presbyopia and hyperopia, a converging lens provides the extra curvature necessary to bring the near point closer to the eye while for myopia a diverging lens
Divergence is a mathematical function that associates a scalar with every point of a vector field.
Divergence, divergent, or variants of the word, may also refer to:
Mathematics
* Divergence (computer science), a computation which does not ter ...
provides the curvature necessary to send the far point to infinity. Astigmatism is corrected with a cylindrical surface lens that curves more strongly in one direction than in another, compensating for the non-uniformity of the cornea.
The optical power of corrective lenses is measured in diopters, a value equal to the reciprocal of the focal length measured in metres; with a positive focal length corresponding to a converging lens and a negative focal length corresponding to a diverging lens. For lenses that correct for astigmatism as well, three numbers are given: one for the spherical power, one for the cylindrical power, and one for the angle of orientation of the astigmatism.
Visual effects
 Optical illusions (also called visual illusions) are characterized by visually perceived images that differ from objective reality. The information gathered by the eye is processed in the brain to give a percept that differs from the object being imaged. Optical illusions can be the result of a variety of phenomena including physical effects that create images that are different from the objects that make them, the physiological effects on the eyes and brain of excessive stimulation (e.g. brightness, tilt, colour, movement), and cognitive illusions where the eye and brain make unconscious inferences.
Cognitive illusions include some which result from the unconscious misapplication of certain optical principles. For example, the Ames room, Hering, M├╝ller-Lyer, Orbison, Ponzo, Sander, and Wundt illusions all rely on the suggestion of the appearance of distance by using converging and diverging lines, in the same way that parallel light rays (or indeed any set of parallel lines) appear to converge at a vanishing point at infinity in two-dimensionally rendered images with artistic perspective. This suggestion is also responsible for the famous moon illusion where the moon, despite having essentially the same angular size, appears much larger near the
Optical illusions (also called visual illusions) are characterized by visually perceived images that differ from objective reality. The information gathered by the eye is processed in the brain to give a percept that differs from the object being imaged. Optical illusions can be the result of a variety of phenomena including physical effects that create images that are different from the objects that make them, the physiological effects on the eyes and brain of excessive stimulation (e.g. brightness, tilt, colour, movement), and cognitive illusions where the eye and brain make unconscious inferences.
Cognitive illusions include some which result from the unconscious misapplication of certain optical principles. For example, the Ames room, Hering, M├╝ller-Lyer, Orbison, Ponzo, Sander, and Wundt illusions all rely on the suggestion of the appearance of distance by using converging and diverging lines, in the same way that parallel light rays (or indeed any set of parallel lines) appear to converge at a vanishing point at infinity in two-dimensionally rendered images with artistic perspective. This suggestion is also responsible for the famous moon illusion where the moon, despite having essentially the same angular size, appears much larger near the horizon
The horizon is the apparent curve that separates the surface of a celestial body from its sky when viewed from the perspective of an observer on or near the surface of the relevant body. This curve divides all viewing directions based on whethe ...
than it does at zenith
The zenith (, ) is the imaginary point on the celestial sphere directly "above" a particular location. "Above" means in the vertical direction (Vertical and horizontal, plumb line) opposite to the gravity direction at that location (nadir). The z ...
. This illusion so confounded Ptolemy
Claudius Ptolemy (; , ; ; ŌĆō 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzant ...
that he incorrectly attributed it to atmospheric refraction when he described it in his treatise, ''Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
''.
Another type of optical illusion exploits broken patterns to trick the mind into perceiving symmetries or asymmetries that are not present. Examples include the caf├® wall, Ehrenstein, Fraser spiral, Poggendorff, and Z├Čllner illusions. Related, but not strictly illusions, are patterns that occur due to the superimposition of periodic structures. For example, transparent tissues with a grid structure produce shapes known as moir├® patterns, while the superimposition of periodic transparent patterns comprising parallel opaque lines or curves produces line moir├® patterns.
Optical instruments
Single lenses have a variety of applications including photographic lenses, corrective lenses, and magnifying glasses while single mirrors are used in parabolic reflectors and rear-view mirrors. Combining a number of mirrors, prisms, and lenses produces compound optical instruments which have practical uses. For example, aperiscope
A periscope is an instrument for observation over, around or through an object, obstacle or condition that prevents direct line-of-sight observation from an observer's current position.
In its simplest form, it consists of an outer case with ...
is simply two plane mirrors aligned to allow for viewing around obstructions. The most famous compound optical instruments in science are the microscope and the telescope which were both invented by the Dutch in the late 16th century.
Microscopes were first developed with just two lenses: an objective lens and an eyepiece. The objective lens is essentially a magnifying glass and was designed with a very small focal length while the eyepiece generally has a longer focal length. This has the effect of producing magnified images of close objects. Generally, an additional source of illumination is used since magnified images are dimmer due to the conservation of energy and the spreading of light rays over a larger surface area. Modern microscopes, known as ''compound microscopes'' have many lenses in them (typically four) to optimize the functionality and enhance image stability. A slightly different variety of microscope, the comparison microscope, looks at side-by-side images to produce a stereoscopic binocular view that appears three dimensional when used by humans.
The first telescopes, called refracting telescopes, were also developed with a single objective and eyepiece lens. In contrast to the microscope, the objective lens of the telescope was designed with a large focal length to avoid optical aberrations. The objective focuses an image of a distant object at its focal point which is adjusted to be at the focal point of an eyepiece of a much smaller focal length. The main goal of a telescope is not necessarily magnification, but rather the collection of light which is determined by the physical size of the objective lens. Thus, telescopes are normally indicated by the diameters of their objectives rather than by the magnification which can be changed by switching eyepieces. Because the magnification of a telescope is equal to the focal length of the objective divided by the focal length of the eyepiece, smaller focal-length eyepieces cause greater magnification.
Since crafting large lenses is much more difficult than crafting large mirrors, most modern telescopes are ''reflecting telescope
A reflecting telescope (also called a reflector) is a telescope that uses a single or a combination of curved mirrors that reflect light and form an image. The reflecting telescope was invented in the 17th century by Isaac Newton as an alternati ...
s'', that is, telescopes that use a primary mirror rather than an objective lens. The same general optical considerations apply to reflecting telescopes that applied to refracting telescopes, namely, the larger the primary mirror, the more light collected, and the magnification is still equal to the focal length of the primary mirror divided by the focal length of the eyepiece. Professional telescopes generally do not have eyepieces and instead place an instrument (often a charge-coupled device) at the focal point instead.
Photography

 The optics of photography involves both lenses and the medium in which the electromagnetic radiation is recorded, whether it be a plate,
The optics of photography involves both lenses and the medium in which the electromagnetic radiation is recorded, whether it be a plate, film
A film, also known as a movie or motion picture, is a work of visual art that simulates experiences and otherwise communicates ideas, stories, perceptions, emotions, or atmosphere through the use of moving images that are generally, sinc ...
, or charge-coupled device. Photographers must consider the reciprocity of the camera and the shot which is summarized by the relation
:Exposure ŌłØ ApertureArea ├Ś ExposureTime ├Ś SceneLuminance
In other words, the smaller the aperture (giving greater depth of focus), the less light coming in, so the length of time has to be increased (leading to possible blurriness if motion occurs). An example of the use of the law of reciprocity is the Sunny 16 rule which gives a rough estimate for the settings needed to estimate the proper exposure in daylight.
A camera's aperture is measured by a unitless number called the f-number or f-stop, #, often notated as , and given by
:
where is the focal length, and is the diameter of the entrance pupil. By convention, "#" is treated as a single symbol, and specific values of # are written by replacing the number sign
The symbol is known as the number sign, hash, (or in North America) the pound sign. The symbol has historically been used for a wide range of purposes including the designation of an ordinal number and as a Typographic ligature, ligatured abbre ...
with the value. The two ways to increase the f-stop are to either decrease the diameter of the entrance pupil or change to a longer focal length (in the case of a zoom lens, this can be done by simply adjusting the lens). Higher f-numbers also have a larger depth of field due to the lens approaching the limit of a pinhole camera which is able to focus all images perfectly, regardless of distance, but requires very long exposure times.
The field of view that the lens will provide changes with the focal length of the lens. There are three basic classifications based on the relationship to the diagonal size of the film or sensor size of the camera to the focal length of the lens:
* Normal lens: angle of view of about 50┬░ (called ''normal'' because this angle considered roughly equivalent to human vision) and a focal length approximately equal to the diagonal of the film or sensor.
* Wide-angle lens: angle of view wider than 60┬░ and focal length shorter than a normal lens.
* Long focus lens: angle of view narrower than a normal lens. This is any lens with a focal length longer than the diagonal measure of the film or sensor. The most common type of long focus lens is the telephoto lens, a design that uses a special ''telephoto group'' to be physically shorter than its focal length.
Modern zoom lenses may have some or all of these attributes.
The absolute value for the exposure time required depends on how sensitive to light the medium being used is (measured by the film speed, or, for digital media, by the quantum efficiency). Early photography used media that had very low light sensitivity, and so exposure times had to be long even for very bright shots. As technology has improved, so has the sensitivity through film cameras and digital cameras.
Other results from physical and geometrical optics apply to camera optics. For example, the maximum resolution capability of a particular camera set-up is determined by the diffraction limit associated with the pupil size and given, roughly, by the Rayleigh criterion.
Atmospheric optics
 The unique optical properties of the atmosphere cause a wide range of spectacular optical phenomena. The blue colour of the sky is a direct result of Rayleigh scattering which redirects higher frequency (blue) sunlight back into the field of view of the observer. Because blue light is scattered more easily than red light, the sun takes on a reddish hue when it is observed through a thick atmosphere, as during a sunrise or
The unique optical properties of the atmosphere cause a wide range of spectacular optical phenomena. The blue colour of the sky is a direct result of Rayleigh scattering which redirects higher frequency (blue) sunlight back into the field of view of the observer. Because blue light is scattered more easily than red light, the sun takes on a reddish hue when it is observed through a thick atmosphere, as during a sunrise or sunset
Sunset (or sundown) is the disappearance of the Sun at the end of the Sun path, below the horizon of the Earth (or any other astronomical object in the Solar System) due to its Earth's rotation, rotation. As viewed from everywhere on Earth, it ...
. Additional particulate matter in the sky can scatter different colours at different angles creating colourful glowing skies at dusk and dawn. Scattering off of ice crystals and other particles in the atmosphere are responsible for halos, afterglows, coronas, rays of sunlight, and sun dogs. The variation in these kinds of phenomena is due to different particle sizes and geometries.
Mirages are optical phenomena in which light rays are bent due to thermal variations in the refraction index of air, producing displaced or heavily distorted images of distant objects. Other dramatic optical phenomena associated with this include the Novaya Zemlya effect where the sun appears to rise earlier than predicted with a distorted shape. A spectacular form of refraction occurs with a temperature inversion called the Fata Morgana where objects on the horizon or even beyond the horizon, such as islands, cliffs, ships or icebergs, appear elongated and elevated, like "fairy tale castles".
Rainbows are the result of a combination of internal reflection and dispersive refraction of light in raindrops. A single reflection off the backs of an array of raindrops produces a rainbow with an angular size on the sky that ranges from 40┬░ to 42┬░ with red on the outside. Double rainbows are produced by two internal reflections with angular size of 50.5┬░ to 54┬░ with violet on the outside. Because rainbows are seen with the sun 180┬░ away from the centre of the rainbow, rainbows are more prominent the closer the sun is to the horizon.
See also
* Ion optics * Important publications in optics * List of optical topics * List of textbooks in electromagnetismReferences
Works cited
* *Further reading
* * * * *External links
;Relevant discussions * ;Textbooks and tutorialsLight and Matter
ŌĆō an open-source textbook, containing a treatment of optics in ch. 28ŌĆō32
Optics2001
ŌĆō Optics library and community
Fundamental Optics
ŌĆō Melles Griot Technical Guide
Physics of Light and Optics
ŌĆō
Brigham Young University
Brigham Young University (BYU) is a Private education, private research university in Provo, Utah, United States. It was founded in 1875 by religious leader Brigham Young and is the flagship university of the Church Educational System sponsore ...
Undergraduate Book
Optics for PV
ŌĆō a step-by-step introduction to classical optics ;Further reading
b
;Societies * European Optical Society ŌĆ
link
* The Optical Society (OSA) ŌĆ
link
* SPIE ŌĆ
link
* European Photonics Industry Consortium ŌĆ
link
{{Authority control > > Applied and interdisciplinary physics Atomic, molecular, and optical physics Natural philosophy