|
Focus (optics)
In geometrical optics, a focus, also called an image point, is a point where light rays originating from a point on the object converge. Although the focus is conceptually a point, physically the focus has a spatial extent, called the blur circle. This non-ideal focusing may be caused by aberrations of the imaging optics. In the absence of significant aberrations, the smallest possible blur circle is the Airy disc, which is caused by diffraction from the optical system's aperture. Aberrations tend to worsen as the aperture diameter increases, while the Airy circle is smallest for large apertures. An image, or image point or region, is in focus if light from object points is converged almost as much as possible in the image, and out of focus if light is not well converged. The border between these is sometimes defined using a "circle of confusion" criterion. A principal focus or focal point is a special focus: * For a lens, or a spherical or parabolic mirror, it is a point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focusing On Retina
Focusing may refer to: * Adjusting an optical system to minimize defocus aberration * Focusing (psychotherapy), a psychotherapeutic technique See also *Focus (other) {{dab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytic geometry, Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focus (geometry)
In geometry, focuses or foci (), singular focus, are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an ''n''-ellipse. Conic sections Defining conics in terms of two foci An ellipse can be defined as the locus of points for which the sum of the distances to two given foci is constant. A circle is the special case of an ellipse in which the two foci coincide with each other. Thus, a circle can be more simply defined as the locus of points each of which is a fixed distance from a single given focus. A circle can also be defined as the circle of Apollonius, in terms of two different foci, as the locus of points having a fixed ratio of distances to the two foci. A parabola is a li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Far Point
In visual perception, the far point is the farthest point at which an object can be placed (along the optical axis of the eye) for its image to be focused on the retina within the eye's accommodation. It is sometimes described as the farthest point from the eye at which images are clear. The other limit of eye's accommodation is the near point. For an unaccommodated emmetropic eye, the far point is at infinity, but for the sake of practicality, infinity is considered to be because the accommodation change from 6 m to infinity is negligible. See visual acuity or Snellen chart for details about 6/6 (m) or 20/20 (ft) vision. For an unaccommodated myopic eye, the far point is closer than 6 m. It depends upon the refractive error of the person's eye. For an unaccommodated hypermetropic eye, incident light must be converging before entering the eye so as to focus on the retina. In this case (the hypermetropic eye) the focus point is behind the retina in virtual space, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Depth Of Focus
Depth of focus is a lens optics concept that measures the tolerance of placement of the image plane (the film plane in a camera) in relation to the lens. In a camera, depth of focus indicates the tolerance of the film's displacement within the camera and is therefore sometimes referred to as "lens-to-film tolerance". ''Depth of focus'' versus ''depth of field'' The phrase ''depth of focus'' is sometimes erroneously used to refer to the ''depth of field'' (DOF), which is the area in front of the lens in acceptable focus, whereas the true meaning of ''depth of focus'' refers to the zone behind the lens wherein the film plane or sensor is placed to produce an in-focus image. ''Depth of focus'' can have two slightly different meanings. The first is the distance over which the image plane can be displaced while a single object plane remains in acceptably sharp focus; the second is the image-side conjugate of depth of field. With the first meaning, the depth of focus is symmetrical ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Depth Of Field
The depth of field (DOF) is the distance between the nearest and the furthest objects that are in acceptably sharp focus in an image captured with a camera. Factors affecting depth of field For cameras that can only focus on one object distance at a time, depth of field is the distance between the nearest and the farthest objects that are in acceptably sharp focus. "Acceptably sharp focus" is defined using a property called the "circle of confusion". The depth of field can be determined by focal length, distance to subject, the acceptable circle of confusion size, and aperture. Limitations of depth of field can sometimes be overcome with various techniques and equipment. The approximate depth of field can be given by: : \text \approx \frac for a given circle of confusion (c), focal length (f), f-number (N), and distance to subject (u). As distance or the size of the acceptable circle of confusion increases, the depth of field increases; however, increasing the size of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Defocus Aberration
In optics, defocus is the aberration in which an image is simply out of focus. This aberration is familiar to anyone who has used a camera, videocamera, microscope, telescope, or binoculars. Optically, defocus refers to a translation of the focus along the optical axis away from the detection surface. In general, defocus reduces the sharpness and contrast of the image. What should be sharp, high-contrast edges in a scene become gradual transitions. Fine detail in the scene is blurred or even becomes invisible. Nearly all image-forming optical devices incorporate some form of focus adjustment to minimize defocus and maximize image quality. In optics and photography The degree of image blurring for a given amount of focus shift depends inversely on the lens f-number. Low f-numbers, such as to 2.8, are very sensitive to defocus and have very shallow depths of focus. High f-numbers, in the 16 to 32 range, are highly tolerant of defocus, and consequently have large dep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardinal Point (optics)
In Gaussian optics, the cardinal points consist of three pairs of points located on the optical axis of a rotationally symmetric, focal, optical system. These are the '' focal points'', the principal points, and the nodal points. For ''ideal'' systems, the basic imaging properties such as image size, location, and orientation are completely determined by the locations of the cardinal points; in fact only four points are necessary: the focal points and either the principal or nodal points. The only ideal system that has been achieved in practice is the plane mirror, however the cardinal points are widely used to ''approximate'' the behavior of real optical systems. Cardinal points provide a way to analytically simplify a system with many components, allowing the imaging characteristics of the system to be approximately determined with simple calculations. Explanation The cardinal points lie on the optical axis of the optical system. Each point is defined by the effect the opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autofocus
An autofocus (or AF) optical system uses a sensor, a control system and a motor to focus on an automatically or manually selected point or area. An electronic rangefinder has a display instead of the motor; the adjustment of the optical system has to be done manually until indication. Autofocus methods are distinguished as active, passive or hybrid types. Autofocus systems rely on one or more sensors to determine correct focus. Some AF systems rely on a single sensor, while others use an array of sensors. Most modern SLR cameras use through-the-lens optical sensors, with a separate sensor array providing light metering, although the latter can be programmed to prioritize its metering to the same area as one or more of the AF sensors. Through-the-lens optical autofocusing is usually speedier and more precise than manual focus with an ordinary viewfinder, although more precise manual focus can be achieved with special accessories such as focusing magnifiers. Autofocus accuracy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
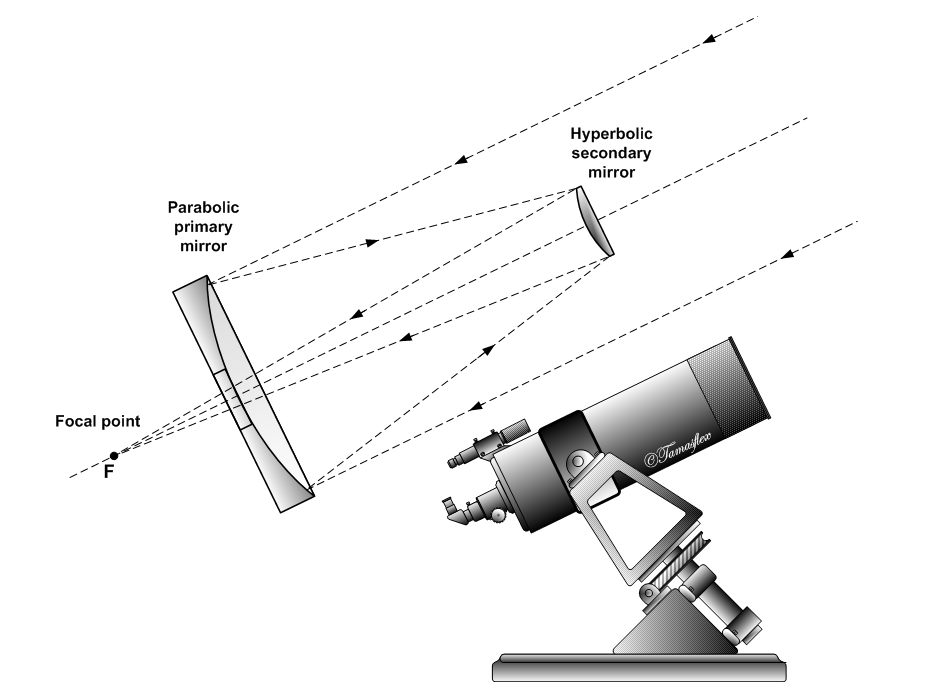
Cassegrain Reflector
The Cassegrain reflector is a combination of a primary concave mirror and a secondary convex mirror, often used in optical telescopes and radio antennas, the main characteristic being that the optical path folds back onto itself, relative to the optical system's primary mirror entrance aperture. This design puts the focal point at a convenient location behind the primary mirror and the convex secondary adds a telephoto effect creating a much longer focal length in a mechanically short system. In a symmetrical Cassegrain both mirrors are aligned about the optical axis, and the primary mirror usually contains a hole in the center, thus permitting the light to reach an eyepiece, a camera, or an image sensor. Alternatively, as in many radio telescopes, the final focus may be in front of the primary. In an asymmetrical Cassegrain, the mirror(s) may be tilted to avoid obscuration of the primary or to avoid the need for a hole in the primary mirror (or both). The classic Cassegrain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focus (geometry)
In geometry, focuses or foci (), singular focus, are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an ''n''-ellipse. Conic sections Defining conics in terms of two foci An ellipse can be defined as the locus of points for which the sum of the distances to two given foci is constant. A circle is the special case of an ellipse in which the two foci coincide with each other. Thus, a circle can be more simply defined as the locus of points each of which is a fixed distance from a single given focus. A circle can also be defined as the circle of Apollonius, in terms of two different foci, as the locus of points having a fixed ratio of distances to the two foci. A parabola is a li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Mirrors
A curved mirror is a mirror with a curved reflecting surface. The surface may be either ''convex'' (bulging outward) or ''concave'' (recessed inward). Most curved mirrors have surfaces that are shaped like part of a sphere, but other shapes are sometimes used in optical devices. The most common non-spherical type are parabolic reflectors, found in optical devices such as reflecting telescopes that need to image distant objects, since spherical mirror systems, like spherical Lens (optics), lenses, suffer from spherical aberration. Distorting mirrors are used for entertainment. They have convex and concave regions that produce deliberately distorted images. They also provide highly magnified or highly diminished (smaller) images when the object is placed at certain distances. Convex mirrors A convex mirror or diverging mirror is a curved mirror in which the reflective surface bulges towards the light source. Convex mirrors reflect light outwards, therefore they are not used to f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |