|
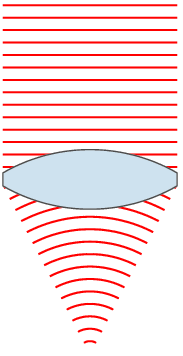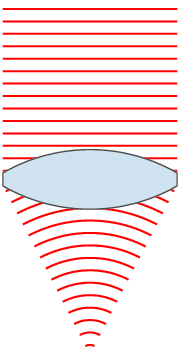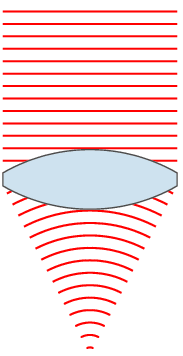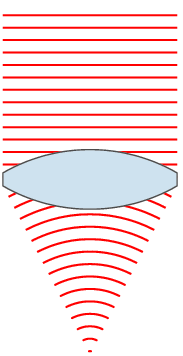
Thin Lens
In optics, a thin lens is a lens with a thickness (distance along the optical axis between the two surfaces of the lens) that is negligible compared to the radii of curvature of the lens surfaces. Lenses whose thickness is not negligible are sometimes called ''thick lenses''. The thin lens approximation ignores optical effects due to the thickness of lenses and simplifies ray tracing calculations. It is often combined with the paraxial approximation in techniques such as ray transfer matrix analysis. Focal length The focal length, ''f'', of a lens in air is given by the lensmaker's equation: :\frac = (n-1) \left \frac - \frac + \frac \right where ''n'' is the index of refraction of the lens material, and ''R''1 and ''R''2 are the radii of curvature of the two surfaces. For a thin lens, ''d'' is much smaller than one of the radii of curvature (either ''R''1 or ''R''2). In these conditions, the last term of the Lensmaker's equation becomes negligible, and the focal length of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Because light is an electromagnetic wave, other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties. Most optical phenomena can be accounted for by using the classical electromagnetic description of light. Complete electromagnetic descriptions of light are, however, often difficult to apply in practice. Practical optics is usually done using simplified models. The most common of these, geometric optics, treats light as a collection of rays that travel in straight lines and bend when they pass through or reflect from surfaces. Physical optics is a more comprehensive model of light, which includes wave effects such as diffraction and interference that cannot be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lens (optics)
A lens is a transmissive optical device which focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements''), usually arranged along a common axis. Lenses are made from materials such as glass or plastic, and are ground and polished or molded to a desired shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing. Devices that similarly focus or disperse waves and radiation other than visible light are also called lenses, such as microwave lenses, electron lenses, acoustic lenses, or explosive lenses. Lenses are used in various imaging devices like telescopes, binoculars and cameras. They are also used as visual aids in glasses to correct defects of vision such as myopia and hypermetropia. History The word ''lens'' comes from '' lēns'', the Latin name of the lentil (a seed of a lentil plant), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Axis
An optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens, microscope or telescopic sight. The optical axis is an imaginary line that defines the path along which light propagates through the system, up to first approximation. For a system composed of simple lenses and mirrors, the axis passes through the center of curvature of each surface, and coincides with the axis of rotational symmetry. The optical axis is often coincident with the system's mechanical axis, but not always, as in the case of off-axis optical systems. For an optical fiber, the optical axis is along the center of the fiber core, and is also known as the ''fiber axis''. See also * Ray (optics) * Cardinal point (optics) * Antenna boresight In telecommunications and radar engineering, antenna boresight is the axis of maximum gain (maximum radiated power) of a directional antenna. For most antennas the boresight is the axis of symmetry of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius Of Curvature (optics)
Radius of curvature (ROC) has specific meaning and sign convention in optical design. A spherical lens or mirror surface has a center of curvature located either along or decentered from the system local optical axis. The vertex of the lens surface is located on the local optical axis. The distance from the vertex to the center of curvature is the radius of curvature of the surface. The sign convention for the optical radius of curvature is as follows: * If the vertex lies to the left of the center of curvature, the radius of curvature is positive. * If the vertex lies to the right of the center of curvature, the radius of curvature is negative. Thus when viewing a biconvex lens from the side, the left surface radius of curvature is positive, and the right radius of curvature is negative. Note however that ''in areas of optics other than design'', other sign conventions are sometimes used. In particular, many undergraduate physics textbooks use the Gaussian sign conventi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ray Tracing (physics)
In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflect off surfaces, complicating analysis. Ray tracing solves the problem by repeatedly advancing idealized narrow beams called ''rays'' through the medium by discrete amounts. Simple problems can be analyzed by propagating a few rays using simple mathematics. More detailed analysis can be performed by using a computer to propagate many rays. When applied to problems of electromagnetic radiation, ray tracing often relies on approximate solutions to Maxwell's equations that are valid as long as the light waves propagate through and around objects whose dimensions are much greater than the light's wavelength. Ray theory does not describe phenomena such as interference and diffraction, which require wave theory (invo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paraxial Approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system (such as a lens). A paraxial ray is a ray which makes a small angle (''θ'') to the optical axis of the system, and lies close to the axis throughout the system. Generally, this allows three important approximations (for ''θ'' in radians) for calculation of the ray's path, namely: : \sin \theta \approx \theta,\quad \tan \theta \approx \theta \quad \text\quad\cos \theta \approx 1. The paraxial approximation is used in Gaussian optics and ''first-order'' ray tracing. Ray transfer matrix analysis is one method that uses the approximation. In some cases, the second-order approximation is also called "paraxial". The approximations above for sine and tangent do not change for the "second-order" paraxial approximation (the second term in their Taylor series expansion is zero), while for cosine the second order approximation is : \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ray Transfer Matrix Analysis
Ray transfer matrix analysis (also known as ABCD matrix analysis) is a mathematical form for performing ray tracing calculations in sufficiently simple problems which can be solved considering only paraxial rays. Each optical element (surface, interface, mirror, or beam travel) is described by a 2×2 ''ray transfer matrix'' which operates on a vector describing an incoming light ray to calculate the outgoing ray. Multiplication of the successive matrices thus yields a concise ray transfer matrix describing the entire optical system. The same mathematics is also used in accelerator physics to track particles through the magnet installations of a particle accelerator, see electron optics. This technique, as described below, is derived using the ''paraxial approximation'', which requires that all ray directions (directions normal to the wavefronts) are at small angles ''θ'' relative to the optical axis of the system, such that the approximation \sin \theta \approx \theta remains val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lensmaker's Equation
A lens is a transmissive optical device which focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements''), usually arranged along a common axis. Lenses are made from materials such as glass or plastic, and are ground and polished or molded to a desired shape. A lens can focus light to form an image, unlike a prism, which refracts light without focusing. Devices that similarly focus or disperse waves and radiation other than visible light are also called lenses, such as microwave lenses, electron lenses, acoustic lenses, or explosive lenses. Lenses are used in various imaging devices like telescopes, binoculars and cameras. They are also used as visual aids in glasses to correct defects of vision such as myopia and hypermetropia. History The word '' lens'' comes from '' lēns'', the Latin name of the lentil (a seed of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Index Of Refraction
In optics, the refractive index (or refraction index) of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium. The refractive index determines how much the path of light is bent, or refracted, when entering a material. This is described by Snell's law of refraction, , where ''θ''1 and ''θ''2 are the angle of incidence and angle of refraction, respectively, of a ray crossing the interface between two media with refractive indices ''n''1 and ''n''2. The refractive indices also determine the amount of light that is reflected when reaching the interface, as well as the critical angle for total internal reflection, their intensity ( Fresnel's equations) and Brewster's angle. The refractive index can be seen as the factor by which the speed and the wavelength of the radiation are reduced with respect to their vacuum values: the speed of light in a medium is , and similarly the wavelength in that medium is , where ''λ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Addison Wesley
Addison-Wesley is an American publisher of textbooks and computer literature. It is an imprint of Pearson PLC, a global publishing and education company. In addition to publishing books, Addison-Wesley also distributes its technical titles through the O'Reilly Online Learning e-reference service. Addison-Wesley's majority of sales derive from the United States (55%) and Europe (22%). The Addison-Wesley Professional Imprint produces content including books, eBooks, and video for the professional IT worker including developers, programmers, managers, system administrators. Classic titles include ''The Art of Computer Programming'', ''The C++ Programming Language'', ''The Mythical Man-Month'', and ''Design Patterns''. History Lew Addison Cummings and Melbourne Wesley Cummings founded Addison-Wesley in 1942, with the first book published by Addison-Wesley being Massachusetts Institute of Technology professor Francis Weston Sears' ''Mechanics''. Its first computer book was ''Progra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign Convention
In physics, a sign convention is a choice of the physical significance of signs (plus or minus) for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of definitions is used consistently. The choices made may differ between authors. Disagreement about sign conventions is a frequent source of confusion, frustration, misunderstandings, and even outright errors in scientific work. In general, a sign convention is a special case of a choice of coordinate system for the case of one dimension. Sometimes, the term "sign convention" is used more broadly to include factors of '' i'' and 2 π, rather than just choices of sign. Relativity Metric signature In relativity, the metric signature can be either or . (Note that throughout this article we are displaying the signs of the eigenvalues of the metric in the order that presents t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |