Network science is an academic field which studies
complex networks such as
telecommunication networks,
computer network
A computer network is a collection of communicating computers and other devices, such as printers and smart phones. In order to communicate, the computers and devices must be connected by wired media like copper cables, optical fibers, or b ...
s,
biological networks,
cognitive and
semantic networks, and
social network
A social network is a social structure consisting of a set of social actors (such as individuals or organizations), networks of Dyad (sociology), dyadic ties, and other Social relation, social interactions between actors. The social network per ...
s, considering distinct elements or actors represented by ''nodes'' (or ''vertices'') and the connections between the elements or actors as ''links'' (or ''edges''). The field draws on theories and methods including
graph theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph ...
from mathematics,
statistical mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applicati ...
from physics,
data mining and
information visualization
Data and information visualization (data viz/vis or info viz/vis) is the practice of designing and creating Graphics, graphic or visual Representation (arts), representations of a large amount of complex quantitative and qualitative data and i ...
from computer science,
inferential modeling from statistics, and
social structure from sociology. The
United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena."
Background and history
The study of networks has emerged in diverse disciplines as a means of analyzing complex relational data. The earliest known paper in this field is the famous
Seven Bridges of Königsberg written by
Leonhard Euler in 1736. Euler's mathematical description of vertices and edges was the foundation of
graph theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph ...
, a branch of mathematics that studies the properties of pairwise relations in a network structure. The field of
graph theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph ...
continued to develop and found applications in chemistry (Sylvester, 1878).
Dénes Kőnig, a Hungarian mathematician and professor, wrote the first book in Graph Theory, entitled "Theory of finite and infinite graphs", in 1936.
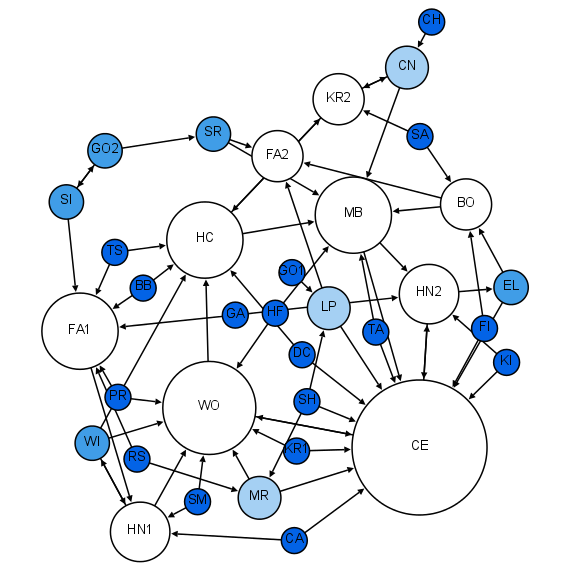
In the 1930s
Jacob Moreno, a psychologist in the
Gestalt tradition, arrived in the United States. He developed the
sociogram and presented it to the public in April 1933 at a convention of medical scholars. Moreno claimed that "before the advent of sociometry no one knew what the interpersonal structure of a group 'precisely' looked like". The sociogram was a representation of the social structure of a group of elementary school students. The boys were friends of boys and the girls were friends of girls with the exception of one boy who said he liked a single girl. The feeling was not reciprocated. This network representation of social structure was found so intriguing that it was printed in
The New York Times
''The New York Times'' (''NYT'') is an American daily newspaper based in New York City. ''The New York Times'' covers domestic, national, and international news, and publishes opinion pieces, investigative reports, and reviews. As one of ...
. The sociogram has found many applications and has grown into the field of
social network analysis.
Probabilistic theory in network science developed as an offshoot of
graph theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph ...
with
Paul Erdős and
Alfréd Rényi's eight famous papers on
random graphs. For
social networks the
exponential random graph model or p* is a notational framework used to represent the probability space of a tie occurring in a
social network
A social network is a social structure consisting of a set of social actors (such as individuals or organizations), networks of Dyad (sociology), dyadic ties, and other Social relation, social interactions between actors. The social network per ...
. An alternate approach to network probability structures is the
network probability matrix, which models the probability of edges occurring in a network, based on the historic presence or absence of the edge in a sample of networks.
Interest in networks exploded around 2000, following new discoveries that offered novel mathematical framework to describe different network topologies, leading to the term 'network science'.
Albert-László Barabási and
Reka Albert discovered the
scale-free networks
nature of many real networks, from the WWW to the cell. The scale-free property captures the fact that in real network hubs coexist with many small degree vertices, and the authors offered a dynamical model to explain the origin of this scale-free state.
and
Steven Strogatz reconciled empirical data on networks with mathematical representation, describing the
small-world network.
Network Classification
Deterministic Network
The definition of deterministic network is defined compared with the definition of probabilistic network. In un-weighted deterministic networks, edges either exist or not, usually we use 0 to represent non-existence of an edge while 1 to represent existence of an edge. In weighted deterministic networks, the edge value represents the weight of each edge, for example, the strength level.
Probabilistic Network
In probabilistic networks, values behind each edge represent the likelihood of the existence of each edge. For example, if one edge has a value equals to 0.9, we say the existence probability of this edge is 0.9.
Network properties
Often, networks have certain attributes that can be calculated to analyze the properties & characteristics of the network. The behavior of these network properties often define
network models and can be used to analyze how certain models contrast to each other. Many of the definitions for other terms used in network science can be found in
Glossary of graph theory.
Size
The size of a network can refer to the number of nodes
or, less commonly, the number of edges
which (for connected graphs with no multi-edges) can range from
(a tree) to
(a complete graph). In the case of a simple graph (a network in which at most one (undirected) edge exists between each pair of vertices, and in which no vertices connect to themselves), we have
; for directed graphs (with no self-connected nodes),
; for directed graphs with self-connections allowed,
. In the circumstance of a graph within which multiple edges may exist between a pair of vertices,
.
Density
The density
of a network is defined as a normalized ratio between 0 and 1 of the number of edges
to the number of possible edges in a network with
nodes. Network density is a measure of the percentage of "optional" edges that exist in the network and can be computed as
where
and
are the minimum and maximum number of edges in a connected network with
nodes, respectively. In the case of simple graphs,
is given by the
binomial coefficient and
, giving density
.
Another possible equation is
whereas the ties
are unidirectional (Wasserman & Faust 1994). This gives a better overview over the network density, because unidirectional relationships can be measured.
Planar network density
The density
of a network, where there is no intersection between edges, is defined as a ratio of the number of edges
to the number of possible edges in a network with
nodes, given by a graph with no intersecting edges
, giving
Average degree
The
degree of a node is the number of edges connected to it. Closely related to the density of a network is the average degree,
(or, in the case of directed graphs,
, the former factor of 2 arising from each edge in an undirected graph contributing to the degree of two distinct vertices). In the
ER random graph model (
) we can compute the expected value of
(equal to the expected value of
of an arbitrary vertex): a random vertex has
other vertices in the network available, and with probability
, connects to each. Thus,
.
Degree distribution
The degree distribution
is a fundamental property of both real networks, such as the
Internet
The Internet (or internet) is the Global network, global system of interconnected computer networks that uses the Internet protocol suite (TCP/IP) to communicate between networks and devices. It is a internetworking, network of networks ...
and
social networks, and of theoretical models. The degree distribution ''P''(''k'') of a network is defined to be the fraction of nodes in the network with degree ''k''. The simplest network model, for example, the (Erdős–Rényi model)
random graph, in which each of ''n'' nodes is independently connected (or not) with probability ''p'' (or 1 − ''p''), has a
binomial distribution of degrees ''k'' (or
Poisson in the limit of large ''n''). Most real networks, from the
WWW to
protein interaction networks, however, have a degree distribution that are highly
right-skewed, meaning that a large majority of nodes have low degree but a small number, known as "hubs", have high degree. For such
scale-free networks the degree distribution approximately follows a
power law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a relative change in the other quantity proportional to the ...
:
, where ''γ'' is the degree exponent, and is a constant. Such
scale-free networks have unexpected structural and dynamical properties, rooted in the diverging second moment of the degree distribution.
Average shortest path length (or characteristic path length)
The average shortest path length is calculated by finding the
shortest path between all pairs of nodes, and taking the average over all paths of the length thereof (the length being the number of intermediate edges contained in the path, i.e., the distance
between the two vertices
within the graph). This shows us, on average, the number of steps it takes to get from one member of the network to another. The behavior of the expected average shortest path length (that is, the ensemble average of the average shortest path length) as a function of the number of vertices
of a random network model defines whether that model exhibits the small-world effect; if it scales as
, the model generates small-world nets. For faster-than-logarithmic growth, the model does not produce small worlds. The special case of
is known as ultra-small world effect.
Diameter of a network
As another means of measuring network graphs, we can define the diameter of a network as the longest of all the calculated shortest paths in a network. It is the shortest distance between the two most distant nodes in the network. In other words, once the shortest path length from every node to all other nodes is calculated, the diameter is the longest of all the calculated path lengths. The diameter is representative of the linear size of a network. If node A-B-C-D are connected, going from A->D this would be the diameter of 3 (3-hops, 3-links).
Clustering coefficient
The clustering coefficient is a measure of an "all-my-friends-know-each-other" property. This is sometimes described as the friends of my friends are my friends. More precisely, the clustering coefficient of a node is the ratio of existing links connecting a node's neighbors to each other to the maximum possible number of such links. The clustering coefficient for the entire network is the average of the clustering coefficients of all the nodes. A high clustering coefficient for a network is another indication of a
small world.
The clustering coefficient of the
'th node is
:
where
is the number of neighbours of the
'th node, and
is the number of connections between these neighbours. The maximum possible number of connections between neighbors is, then,
:
From a probabilistic standpoint, the expected local clustering coefficient is the likelihood of a link existing between two arbitrary neighbors of the same node.
Connectedness
The way in which a network is connected plays a large part into how networks are analyzed and interpreted. Networks are classified in four different categories:
* ''Clique''/''Complete Graph'': a completely connected network, where all nodes are connected to every other node. These networks are symmetric in that all nodes have in-links and out-links from all others.
* ''Giant Component'': A single connected component which contains most of the nodes in the network.
* ''Weakly Connected Component'': A collection of nodes in which there exists a path from any node to any other, ignoring directionality of the edges.
* ''Strongly Connected Component'': A collection of nodes in which there exists a ''directed'' path from any node to any other.
Node centrality
Centrality indices produce rankings which seek to identify the most important nodes in a network model. Different centrality indices encode different contexts for the word "importance." The
betweenness centrality, for example, considers a node highly important if it form bridges between many other nodes. The
eigenvalue centrality, in contrast, considers a node highly important if many other highly important nodes link to it. Hundreds of such measures have been proposed in the literature.
Centrality indices are only accurate for identifying the most important nodes. The measures are seldom, if ever, meaningful for the remainder of network nodes.
[
][
] Also, their indications are only accurate within their assumed context for importance, and tend to "get it wrong" for other contexts.
[
] For example, imagine two separate communities whose only link is an edge between the most junior member of each community. Since any transfer from one community to the other must go over this link, the two junior members will have high betweenness centrality. But, since they are junior, (presumably) they have few connections to the "important" nodes in their community, meaning their eigenvalue centrality would be quite low.
Node influence
Limitations to centrality measures have led to the development of more general measures.
Two examples are
the accessibility, which uses the diversity of random walks to measure how accessible the rest of the network is from a given start node,
and the expected force, derived from the expected value of the
force of infection generated by a node.
Both of these measures can be meaningfully computed from the structure of the network alone.
Community structure
Nodes in a network may be partitioned into groups representing communities. Depending on the context, communities may be distinct or overlapping. Typically, nodes in such communities will be strongly connected to other nodes in the same community, but weakly connected to nodes outside the community. In the absence of a
ground truth describing the
community structure of a specific network, several algorithms have been developed to infer possible community structures using either supervised of unsupervised clustering methods.
Network models
Network models serve as a foundation to understanding interactions within empirical complex networks. Various
random graph generation models produce network structures that may be used in comparison to real-world complex networks.
Erdős–Rényi random graph model

The
Erdős–Rényi model, named for
Paul Erdős and
Alfréd Rényi, is used for generating
random graphs in which edges are set between nodes with equal probabilities. It can be used in the
probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs.
To generate an Erdős–Rényi model
two parameters must be specified: the total number of nodes and the probability that a random pair of nodes has an edge.
Because the model is generated without bias to particular nodes, the degree distribution is binomial: for a randomly chosen vertex
,
:
In this model the clustering coefficient is
a.s. The behavior of
can be broken into three regions.
''Subcritical''
: All components are simple and very small, the largest component has size
;
''Critical''
:
;
''Supercritical''
:
where
is the positive solution to the equation
.
The largest connected component has high complexity. All other components are simple and small
.
Configuration model
The configuration model takes a degree sequence
or degree distribution
(which subsequently is used to generate a degree sequence) as the input, and produces randomly connected graphs in all respects other than the degree sequence. This means that for a given choice of the degree sequence, the graph is chosen uniformly at random from the set of all graphs that comply with this degree sequence. The degree
of a randomly chosen vertex is an
independent and identically distributed random variable with integer values. When
, the configuration graph contains the
giant connected component, which has infinite size.
The rest of the components have finite sizes, which can be quantified with the notion of the size distribution. The probability
that a randomly sampled node is connected to a component of size
is given by
convolution powers of the degree distribution:
where
denotes the degree distribution and
. The giant component can be destroyed by randomly removing the critical fraction
of all edges. This process is called
percolation on random networks. When the second moment of the degree distribution is finite,
, this critical edge fraction is given by
, and the
average vertex-vertex distance in the giant component scales logarithmically with the total size of the network,
.
In the directed configuration model, the degree of a node is given by two numbers, in-degree
and out-degree
, and consequently, the degree distribution is two-variate. The expected number of in-edges and out-edges coincides, so that
 In the 1930s Jacob Moreno, a psychologist in the Gestalt tradition, arrived in the United States. He developed the sociogram and presented it to the public in April 1933 at a convention of medical scholars. Moreno claimed that "before the advent of sociometry no one knew what the interpersonal structure of a group 'precisely' looked like". The sociogram was a representation of the social structure of a group of elementary school students. The boys were friends of boys and the girls were friends of girls with the exception of one boy who said he liked a single girl. The feeling was not reciprocated. This network representation of social structure was found so intriguing that it was printed in
In the 1930s Jacob Moreno, a psychologist in the Gestalt tradition, arrived in the United States. He developed the sociogram and presented it to the public in April 1933 at a convention of medical scholars. Moreno claimed that "before the advent of sociometry no one knew what the interpersonal structure of a group 'precisely' looked like". The sociogram was a representation of the social structure of a group of elementary school students. The boys were friends of boys and the girls were friends of girls with the exception of one boy who said he liked a single girl. The feeling was not reciprocated. This network representation of social structure was found so intriguing that it was printed in  The Erdős–Rényi model, named for Paul Erdős and Alfréd Rényi, is used for generating random graphs in which edges are set between nodes with equal probabilities. It can be used in the probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs.
To generate an Erdős–Rényi model two parameters must be specified: the total number of nodes and the probability that a random pair of nodes has an edge.
Because the model is generated without bias to particular nodes, the degree distribution is binomial: for a randomly chosen vertex ,
:
In this model the clustering coefficient is a.s. The behavior of can be broken into three regions.
''Subcritical'' : All components are simple and very small, the largest component has size ;
''Critical'' : ;
''Supercritical'' : where is the positive solution to the equation .
The largest connected component has high complexity. All other components are simple and small .
The Erdős–Rényi model, named for Paul Erdős and Alfréd Rényi, is used for generating random graphs in which edges are set between nodes with equal probabilities. It can be used in the probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs.
To generate an Erdős–Rényi model two parameters must be specified: the total number of nodes and the probability that a random pair of nodes has an edge.
Because the model is generated without bias to particular nodes, the degree distribution is binomial: for a randomly chosen vertex ,
:
In this model the clustering coefficient is a.s. The behavior of can be broken into three regions.
''Subcritical'' : All components are simple and very small, the largest component has size ;
''Critical'' : ;
''Supercritical'' : where is the positive solution to the equation .
The largest connected component has high complexity. All other components are simple and small .
 In the 1930s Jacob Moreno, a psychologist in the Gestalt tradition, arrived in the United States. He developed the sociogram and presented it to the public in April 1933 at a convention of medical scholars. Moreno claimed that "before the advent of sociometry no one knew what the interpersonal structure of a group 'precisely' looked like". The sociogram was a representation of the social structure of a group of elementary school students. The boys were friends of boys and the girls were friends of girls with the exception of one boy who said he liked a single girl. The feeling was not reciprocated. This network representation of social structure was found so intriguing that it was printed in
In the 1930s Jacob Moreno, a psychologist in the Gestalt tradition, arrived in the United States. He developed the sociogram and presented it to the public in April 1933 at a convention of medical scholars. Moreno claimed that "before the advent of sociometry no one knew what the interpersonal structure of a group 'precisely' looked like". The sociogram was a representation of the social structure of a group of elementary school students. The boys were friends of boys and the girls were friends of girls with the exception of one boy who said he liked a single girl. The feeling was not reciprocated. This network representation of social structure was found so intriguing that it was printed in