|
Sequential Dynamical System
Sequential dynamical systems (SDSs) are a class of graph dynamical systems. They are discrete dynamical systems which generalize many aspects of for example classical cellular automata, and they provide a framework for studying asynchronous processes over graphs. The analysis of SDSs uses techniques from combinatorics, abstract algebra, graph theory, dynamical systems and probability theory. Definition An SDS is constructed from the following components: * A finite ''graph'' ''Y'' with vertex set v 'Y''= . Depending on the context the graph can be directed or undirected. * A state ''xv'' for each vertex ''i'' of ''Y'' taken from a finite set ''K''. The ''system state'' is the ''n''-tuple ''x'' = (''x''1, ''x''2, ... , ''xn''), and ''x'' 'i''is the tuple consisting of the states associated to the vertices in the 1-neighborhood of ''i'' in ''Y'' (in some fixed order). * A ''vertex function'' ''fi'' for each vertex ''i''. The vertex function maps the state of vertex ''i'' at time ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Dynamical System
In mathematics, the concept of graph dynamical systems can be used to capture a wide range of processes taking place on graphs or networks. A major theme in the mathematical and computational analysis of GDSs is to relate their structural properties (e.g. the network connectivity) and the global dynamics that result. The work on GDSs considers finite graphs and finite state spaces. As such, the research typically involves techniques from, e.g., graph theory, combinatorics, algebra, and dynamical systems rather than differential geometry. In principle, one could define and study GDSs over an infinite graph (e.g. cellular automata or probabilistic cellular automata over \mathbb^k or interacting particle systems when some randomness is included), as well as GDSs with infinite state space (e.g. \mathbb as in coupled map lattices); see, for example, Wu. In the following, everything is implicitly assumed to be finite unless stated otherwise. Formal definition A graph dynamical system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Networks
Network, networking and networked may refer to: Science and technology * Network theory, the study of graphs as a representation of relations between discrete objects * Network science, an academic field that studies complex networks Mathematics * Networks, a graph with attributes studied in network theory ** Scale-free network, a network whose degree distribution follows a power law ** Small-world network, a mathematical graph in which most nodes are not neighbors, but have neighbors in common * Flow network, a directed graph where each edge has a capacity and each edge receives a flow Biology * Biological network, any network that applies to biological systems * Ecological network, a representation of interacting species in an ecosystem * Neural network, a network or circuit of neurons Technology and communication * Artificial neural network, a computing system inspired by animal brains * Broadcast network, radio stations, television stations, or other electronic media outlet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics, graph theory is the study of '' graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by ''edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science. Combinatorics is well known for the breadth of the problems it tackles. Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving an ''ad hoc'' solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
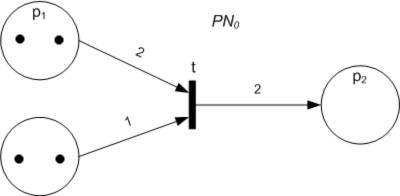
Petri Net
A Petri net, also known as a place/transition (PT) net, is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements, places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri—at the age of 13—for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Petri nets ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Bayesian Network
A Dynamic Bayesian Network (DBN) is a Bayesian network (BN) which relates variables to each other over adjacent time steps. This is often called a ''Two-Timeslice'' BN (2TBN) because it says that at any point in time T, the value of a variable can be calculated from the internal regressors and the immediate prior value (time T-1). DBNs were developed by Paul Dagum in the early 1990s at Stanford University's Section on Medical Informatics. Dagum developed DBNs to unify and extend traditional linear state-space models such as Kalman filters, linear and normal forecasting models such as ARMA and simple dependency models such as hidden Markov models into a general probabilistic representation and inference mechanism for arbitrary nonlinear and non-normal time-dependent domains. Today, DBNs are common in robotics, and have shown potential for a wide range of data mining applications. For example, they have been used in speech recognition, digital forensics, protein sequencing, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gene Regulatory Network
A gene (or genetic) regulatory network (GRN) is a collection of molecular regulators that interact with each other and with other substances in the cell to govern the gene expression levels of mRNA and proteins which, in turn, determine the function of the cell. GRN also play a central role in morphogenesis, the creation of body structures, which in turn is central to evolutionary developmental biology (evo-devo). The regulator can be DNA, RNA, protein or any combination of two or more of these three that form a complex, such as a specific sequence of DNA and a transcription factor to activate that sequence. The interaction can be direct or indirect (through transcribed RNA or translated protein). In general, each mRNA molecule goes on to make a specific protein (or set of proteins). In some cases this protein will be structural, and will accumulate at the cell membrane or within the cell to give it particular structural properties. In other cases the protein will be an enzyme, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Network
A Boolean network consists of a discrete set of boolean variables each of which has a Boolean function (possibly different for each variable) assigned to it which takes inputs from a subset of those variables and output that determines the state of the variable it is assigned to. This set of functions in effect determines a topology (connectivity) on the set of variables, which then become nodes in a network. Usually, the dynamics of the system is taken as a discrete time series where the state of the entire network at time ''t''+1 is determined by evaluating each variable's function on the state of the network at time ''t''. This may be done synchronously or asynchronously. Boolean networks have been used in biology to model regulatory networks. Although Boolean networks are a crude simplification of genetic reality where genes are not simple binary switches, there are several cases where they correctly convey the correct pattern of expressed and suppressed genes. The se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tuple
In mathematics, a tuple is a finite ordered list (sequence) of elements. An -tuple is a sequence (or ordered list) of elements, where is a non-negative integer. There is only one 0-tuple, referred to as ''the empty tuple''. An -tuple is defined inductively using the construction of an ordered pair. Mathematicians usually write tuples by listing the elements within parentheses "" and separated by a comma and a space; for example, denotes a 5-tuple. Sometimes other symbols are used to surround the elements, such as square brackets " nbsp; or angle brackets "⟨ ⟩". Braces "" are used to specify arrays in some programming languages but not in mathematical expressions, as they are the standard notation for sets. The term ''tuple'' can often occur when discussing other mathematical objects, such as vectors. In computer science, tuples come in many forms. Most typed functional programming languages implement tuples directly as product types, tightly associated with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Dynamical System
In mathematics, the concept of graph dynamical systems can be used to capture a wide range of processes taking place on graphs or networks. A major theme in the mathematical and computational analysis of GDSs is to relate their structural properties (e.g. the network connectivity) and the global dynamics that result. The work on GDSs considers finite graphs and finite state spaces. As such, the research typically involves techniques from, e.g., graph theory, combinatorics, algebra, and dynamical systems rather than differential geometry. In principle, one could define and study GDSs over an infinite graph (e.g. cellular automata or probabilistic cellular automata over \mathbb^k or interacting particle systems when some randomness is included), as well as GDSs with infinite state space (e.g. \mathbb as in coupled map lattices); see, for example, Wu. In the following, everything is implicitly assumed to be finite unless stated otherwise. Formal definition A graph dynamical system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |