force (physics) on:
[Wikipedia]
[Google]
[Amazon]
In
 Since antiquity the concept of force has been recognized as integral to the functioning of each of the
Since antiquity the concept of force has been recognized as integral to the functioning of each of the

 Forces act in a particular direction and have
Forces act in a particular direction and have  Free-body diagrams can be used as a convenient way to keep track of forces acting on a system. Ideally, these diagrams are drawn with the angles and relative magnitudes of the force vectors preserved so that graphical vector addition can be done to determine the net force.
As well as being added, forces can also be resolved into independent components at
Free-body diagrams can be used as a convenient way to keep track of forces acting on a system. Ideally, these diagrams are drawn with the angles and relative magnitudes of the force vectors preserved so that graphical vector addition can be done to determine the net force.
As well as being added, forces can also be resolved into independent components at
 Dynamic equilibrium was first described by
Dynamic equilibrium was first described by
 What we now call gravity was not identified as a universal force until the work of Isaac Newton. Before Newton, the tendency for objects to fall towards the Earth was not understood to be related to the motions of celestial objects. Galileo was instrumental in describing the characteristics of falling objects by determining that the
What we now call gravity was not identified as a universal force until the work of Isaac Newton. Before Newton, the tendency for objects to fall towards the Earth was not understood to be related to the motions of celestial objects. Galileo was instrumental in describing the characteristics of falling objects by determining that the
 When objects are in contact, the force directly between them is called the normal force, the component of the total force in the system exerted normal to the interface between the objects. The normal force is closely related to Newton's third law. The normal force, for example, is responsible for the structural integrity of tables and floors as well as being the force that responds whenever an external force pushes on a solid object. An example of the normal force in action is the impact force on an object crashing into an immobile surface.
When objects are in contact, the force directly between them is called the normal force, the component of the total force in the system exerted normal to the interface between the objects. The normal force is closely related to Newton's third law. The normal force, for example, is responsible for the structural integrity of tables and floors as well as being the force that responds whenever an external force pushes on a solid object. An example of the normal force in action is the impact force on an object crashing into an immobile surface.
 A simple elastic force acts to return a spring to its natural length. An ideal spring is taken to be massless, frictionless, unbreakable, and infinitely stretchable. Such springs exert forces that push when contracted, or pull when extended, in proportion to the
A simple elastic force acts to return a spring to its natural length. An ideal spring is taken to be massless, frictionless, unbreakable, and infinitely stretchable. Such springs exert forces that push when contracted, or pull when extended, in proportion to the
 Newton's laws and Newtonian mechanics in general were first developed to describe how forces affect idealized
Newton's laws and Newtonian mechanics in general were first developed to describe how forces affect idealized
 Forces that cause extended objects to rotate are associated with
Forces that cause extended objects to rotate are associated with
 In modern
In modern
 Newton's law of gravitation is an example of ''action at a distance'': one body, like the Sun, exerts an influence upon any other body, like the Earth, no matter how far apart they are. Moreover, this action at a distance is ''instantaneous.'' According to Newton's theory, the one body shifting position changes the gravitational pulls felt by all other bodies, all at the same instant of time.
Newton's law of gravitation is an example of ''action at a distance'': one body, like the Sun, exerts an influence upon any other body, like the Earth, no matter how far apart they are. Moreover, this action at a distance is ''instantaneous.'' According to Newton's theory, the one body shifting position changes the gravitational pulls felt by all other bodies, all at the same instant of time.
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, a force is an influence that can cause an object to change its velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the magnitude and direction of a force are both important, force is a vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
quantity. The SI unit
The International System of Units, internationally known by the abbreviation SI (from French ), is the modern form of the metric system and the world's most widely used system of units of measurement, system of measurement. It is the only system ...
of force is the newton (N), and force is often represented by the symbol .
Force plays an important role in classical mechanics. The concept of force is central to all three of Newton's laws of motion
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body re ...
. Types of forces often encountered in classical mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics inv ...
include elastic
Elastic is a word often used to describe or identify certain types of elastomer, Elastic (notion), elastic used in garments or stretch fabric, stretchable fabrics.
Elastic may also refer to:
Alternative name
* Rubber band, ring-shaped band of rub ...
, friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
al, contact or "normal" forces, and gravitational. The rotational version of force is torque
In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force (also abbreviated to moment). The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. Wh ...
, which produces changes in the rotational speed of an object. In an extended body, each part applies forces on the adjacent parts; the distribution of such forces through the body is the internal mechanical stress. In the case of multiple forces, if the net force on an extended body is zero the body is in equilibrium.
In modern physics
Modern physics is a branch of physics that developed in the early 20th century and onward or branches greatly influenced by early 20th century physics. Notable branches of modern physics include quantum mechanics, special relativity, and genera ...
, which includes relativity and quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, the laws governing motion are revised to rely on fundamental interactions
In physics, the fundamental interactions or fundamental forces are interactions in nature that appear not to be reducible to more basic interactions. There are four fundamental interactions known to exist:
* gravity
* electromagnetism
* weak int ...
as the ultimate origin of force. However, the understanding of force provided by classical mechanics is useful for practical purposes.
Development of the concept
Philosophers in antiquity used the concept of force in the study of stationary and moving objects andsimple machine
A simple machine is a machine, mechanical device that changes the Direction (geometry) , direction or Magnitude_(mathematics) , magnitude of a force. In general, they can be defined as the simplest Mechanism (engineering) , mechanisms that use ...
s, but thinkers such as Aristotle
Aristotle (; 384–322 BC) was an Ancient Greek philosophy, Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, a ...
and Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
retained fundamental errors in understanding force. In part, this was due to an incomplete understanding of the sometimes non-obvious force of friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
and a consequently inadequate view of the nature of natural motion. A fundamental error was the belief that a force is required to maintain motion, even at a constant velocity. Most of the previous misunderstandings about motion and force were eventually corrected by Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642), commonly referred to as Galileo Galilei ( , , ) or mononymously as Galileo, was an Italian astronomer, physicist and engineer, sometimes described as a poly ...
and Sir Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Enlightenment that followed. His book (''Mathe ...
. With his mathematical insight, Newton formulated laws of motion that were not improved for over two hundred years.
By the early 20th century, Einstein developed a theory of relativity
The theory of relativity usually encompasses two interrelated physics theories by Albert Einstein: special relativity and general relativity, proposed and published in 1905 and 1915, respectively. Special relativity applies to all physical ph ...
that correctly predicted the action of forces on objects with increasing momenta near the speed of light and also provided insight into the forces produced by gravitation and inertia
Inertia is the natural tendency of objects in motion to stay in motion and objects at rest to stay at rest, unless a force causes the velocity to change. It is one of the fundamental principles in classical physics, and described by Isaac Newto ...
. With modern insights into quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
and technology that can accelerate particles close to the speed of light, particle physics
Particle physics or high-energy physics is the study of Elementary particle, fundamental particles and fundamental interaction, forces that constitute matter and radiation. The field also studies combinations of elementary particles up to the s ...
has devised a Standard Model
The Standard Model of particle physics is the Scientific theory, theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions – excluding gravity) in the unive ...
to describe forces between particles smaller than atoms. The Standard Model
The Standard Model of particle physics is the Scientific theory, theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions – excluding gravity) in the unive ...
predicts that exchanged particles called gauge bosons are the fundamental means by which forces are emitted and absorbed. Only four main interactions are known: in order of decreasing strength, they are: strong, electromagnetic
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interacti ...
, weak, and gravitational. High-energy particle physics observation
Observation in the natural sciences is an act or instance of noticing or perceiving and the acquisition of information from a primary source. In living beings, observation employs the senses. In science, observation can also involve the percep ...
s made during the 1970s and 1980s confirmed that the weak and electromagnetic forces are expressions of a more fundamental electroweak
In particle physics, the electroweak interaction or electroweak force is the unified description of two of the fundamental interactions of nature: electromagnetism (electromagnetic interaction) and the weak interaction. Although these two forc ...
interaction.
Pre-Newtonian concepts
 Since antiquity the concept of force has been recognized as integral to the functioning of each of the
Since antiquity the concept of force has been recognized as integral to the functioning of each of the simple machine
A simple machine is a machine, mechanical device that changes the Direction (geometry) , direction or Magnitude_(mathematics) , magnitude of a force. In general, they can be defined as the simplest Mechanism (engineering) , mechanisms that use ...
s. The mechanical advantage given by a simple machine allowed for less force to be used in exchange for that force acting over a greater distance for the same amount of work. Analysis of the characteristics of forces ultimately culminated in the work of Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
who was especially famous for formulating a treatment of buoyant forces inherent in fluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...
s.
Aristotle
Aristotle (; 384–322 BC) was an Ancient Greek philosophy, Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, a ...
provided a philosophical discussion of the concept of a force as an integral part of Aristotelian cosmology. In Aristotle's view, the terrestrial sphere contained four elements that come to rest at different "natural places" therein. Aristotle believed that motionless objects on Earth, those composed mostly of the elements earth and water, were in their natural place when on the ground, and that they stay that way if left alone. He distinguished between the innate tendency of objects to find their "natural place" (e.g., for heavy bodies to fall), which led to "natural motion", and unnatural or forced motion, which required continued application of a force. This theory, based on the everyday experience of how objects move, such as the constant application of a force needed to keep a cart moving, had conceptual trouble accounting for the behavior of projectile
A projectile is an object that is propelled by the application of an external force and then moves freely under the influence of gravity and air resistance. Although any objects in motion through space are projectiles, they are commonly found ...
s, such as the flight of arrows. An archer causes the arrow to move at the start of the flight, and it then sails through the air even though no discernible efficient cause acts upon it. Aristotle was aware of this problem and proposed that the air displaced through the projectile's path carries the projectile to its target. This explanation requires a continuous medium such as air to sustain the motion.
Though Aristotelian physics was criticized as early as the 6th century, its shortcomings would not be corrected until the 17th century work of Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642), commonly referred to as Galileo Galilei ( , , ) or mononymously as Galileo, was an Italian astronomer, physicist and engineer, sometimes described as a poly ...
, who was influenced by the late medieval idea that objects in forced motion carried an innate force of impetus. Galileo constructed an experiment in which stones and cannonballs were both rolled down an incline to disprove the Aristotelian theory of motion. He showed that the bodies were accelerated by gravity to an extent that was independent of their mass and argued that objects retain their velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
unless acted on by a force, for example friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
. Galileo's idea that force is needed to change motion rather than to sustain it, further improved upon by Isaac Beeckman, René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramou ...
, and Pierre Gassendi
Pierre Gassendi (; also Pierre Gassend, Petrus Gassendi, Petrus Gassendus; 22 January 1592 – 24 October 1655) was a French philosopher, Catholic priest, astronomer, and mathematician. While he held a church position in south-east France, he a ...
, became a key principle of Newtonian physics.
In the early 17th century, before Newton's '' Principia'', the term "force" () was applied to many physical and non-physical phenomena, e.g., for an acceleration of a point. The product of a point mass and the square of its velocity was named (live force) by Leibniz. The modern concept of force corresponds to Newton's (accelerating force).
Newtonian mechanics
Sir Isaac Newton described the motion of all objects using the concepts ofinertia
Inertia is the natural tendency of objects in motion to stay in motion and objects at rest to stay at rest, unless a force causes the velocity to change. It is one of the fundamental principles in classical physics, and described by Isaac Newto ...
and force. In 1687, Newton published his magnum opus, ''Philosophiæ Naturalis Principia Mathematica
(English: ''The Mathematical Principles of Natural Philosophy''), often referred to as simply the (), is a book by Isaac Newton that expounds Newton's laws of motion and his law of universal gravitation. The ''Principia'' is written in Lati ...
''. This is a recent translation into English by I. Bernard Cohen and Anne Whitman, with help from Julia Budenz. In this work Newton set out three laws of motion that have dominated the way forces are described in physics to this day. The precise ways in which Newton's laws are expressed have evolved in step with new mathematical approaches.
First law
Newton's first law of motion states that the natural behavior of an object at rest is to continue being at rest, and the natural behavior of an object moving at constant speed in a straight line is to continue moving at that constant speed along that straight line. The latter follows from the former because of the principle that the laws of physics are the same for all inertial observers, i.e., all observers who do not feel themselves to be in motion. An observer moving in tandem with an object will see it as being at rest. So, its natural behavior will be to remain at rest with respect to that observer, which means that an observer who sees it moving at constant speed in a straight line will see it continuing to do so.
Second law
According to the first law, motion at constant speed in a straight line does not need a cause. It is ''change'' in motion that requires a cause, and Newton's second law gives the quantitative relationship between force and change of motion.Newton's second law
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body re ...
states that the net force acting upon an object is equal to the rate at which its momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
changes with time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ...
. If the mass of the object is constant, this law implies that the acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector ...
of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
of the object.
A modern statement of Newton's second law is a vector equation:
where is the momentum of the system, and is the net (vector sum
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Euclidean vectors can be added and scal ...
) force. If a body is in equilibrium, there is zero ''net'' force by definition (balanced forces may be present nevertheless). In contrast, the second law states that if there is an ''unbalanced'' force acting on an object it will result in the object's momentum changing over time.
In common engineering applications the mass in a system remains constant allowing as simple algebraic form for the second law. By the definition of momentum,
where ''m'' is the mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
and is the velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
. If Newton's second law is applied to a system of constant mass, ''m'' may be moved outside the derivative operator. The equation then becomes
By substituting the definition of acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector ...
, the algebraic version of Newton's second law
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body re ...
is derived:
Third law
Whenever one body exerts a force on another, the latter simultaneously exerts an equal and opposite force on the first. In vector form, if is the force of body 1 on body 2 and that of body 2 on body 1, then This law is sometimes referred to as the ''action-reaction law'', with called the ''action'' and the ''reaction
Reaction may refer to a process or to a response to an action, event, or exposure.
Physics and chemistry
*Chemical reaction
*Nuclear reaction
*Reaction (physics), as defined by Newton's third law
* Chain reaction (disambiguation)
Biology and ...
''.
Newton's third law is a result of applying symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
to situations where forces can be attributed to the presence of different objects. The third law means that all forces are ''interactions'' between different bodies. and thus that there is no such thing as a unidirectional force or a force that acts on only one body.
In a system composed of object 1 and object 2, the net force on the system due to their mutual interactions is zero:
More generally, in a closed system
A closed system is a natural physical system that does not allow transfer of matter in or out of the system, althoughin the contexts of physics, chemistry, engineering, etc.the transfer of energy (e.g. as work or heat) is allowed.
Physics
In cl ...
of particles, all internal forces are balanced. The particles may accelerate with respect to each other but the center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d ...
of the system will not accelerate. If an external force acts on the system, it will make the center of mass accelerate in proportion to the magnitude of the external force divided by the mass of the system.
Combining Newton's second and third laws, it is possible to show that the linear momentum of a system is conserved in any closed system
A closed system is a natural physical system that does not allow transfer of matter in or out of the system, althoughin the contexts of physics, chemistry, engineering, etc.the transfer of energy (e.g. as work or heat) is allowed.
Physics
In cl ...
. In a system of two particles, if is the momentum of object 1 and the momentum of object 2, then
Using similar arguments, this can be generalized to a system with an arbitrary number of particles. In general, as long as all forces are due to the interaction of objects with mass, it is possible to define a system such that net momentum is never lost nor gained.
Defining "force"
Some textbooks use Newton's second law as a ''definition'' of force. However, for the equation for a constant mass to then have any predictive content, it must be combined with further information. Moreover, inferring that a force is present because a body is accelerating is only valid in an inertial frame of reference. The question of which aspects of Newton's laws to take as definitions and which to regard as holding physical content has been answered in various ways, which ultimately do not affect how the theory is used in practice. Notable physicists, philosophers and mathematicians who have sought a more explicit definition of the concept of force includeErnst Mach
Ernst Waldfried Josef Wenzel Mach ( ; ; 18 February 1838 – 19 February 1916) was an Austrian physicist and philosopher, who contributed to the understanding of the physics of shock waves. The ratio of the speed of a flow or object to that of ...
and Walter Noll
Walter Noll (January 7, 1925 June 6, 2017) was a mathematician, and Professor Emeritus at Carnegie Mellon University. He is best known for developing mathematical tools of classical mechanics, thermodynamics, and continuum mechanics.
Biography
B ...
.
Combining forces
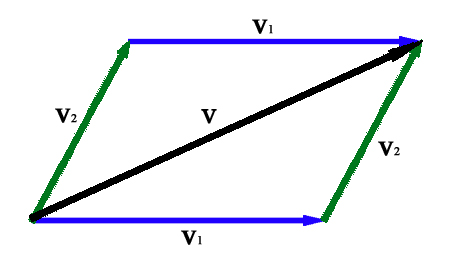
 Forces act in a particular direction and have
Forces act in a particular direction and have sizes
Size in general is the Magnitude (mathematics), magnitude or dimensions of a thing. More specifically, ''geometrical size'' (or ''spatial size'') can refer to three geometrical measures: length, area, or volume. Length can be generalized ...
dependent upon how strong the push or pull is. Because of these characteristics, forces are classified as " vector quantities". This means that forces follow a different set of mathematical rules than physical quantities that do not have direction (denoted scalar quantities). For example, when determining what happens when two forces act on the same object, it is necessary to know both the magnitude and the direction of both forces to calculate the result
A result (also called upshot) is the outcome or consequence of a sequence of actions or events. Possible results include gain, injury, value, and victory. Some types of results include the outcome of an action, the final value of a calculation ...
. If both of these pieces of information are not known for each force, the situation is ambiguous.
Historically, forces were first quantitatively investigated in conditions of static equilibrium
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is ze ...
where several forces canceled each other out. Such experiments demonstrate the crucial properties that forces are additive vector quantities: they have magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
and direction. When two forces act on a point particle
A point particle, ideal particle or point-like particle (often spelled pointlike particle) is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension; being dimensionless, it does not take ...
, the resulting force, the ''resultant'' (also called the ''net force
In mechanics, the net force is the sum of all the forces acting on an object. For example, if two forces are acting upon an object in opposite directions, and one force is greater than the other, the forces can be replaced with a single force tha ...
''), can be determined by following the parallelogram rule of vector addition
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
: the addition of two vectors represented by sides of a parallelogram, gives an equivalent resultant vector that is equal in magnitude and direction to the transversal of the parallelogram. The magnitude of the resultant varies from the difference of the magnitudes of the two forces to their sum, depending on the angle between their lines of action.
right angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the ad ...
s to each other. A horizontal force pointing northeast can therefore be split into two forces, one pointing north, and one pointing east. Summing these component forces using vector addition yields the original force. Resolving force vectors into components of a set of basis vector
In mathematics, a set of elements of a vector space is called a basis (: bases) if every element of can be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as ...
s is often a more mathematically clean way to describe forces than using magnitudes and directions. This is because, for orthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...
components, the components of the vector sum are uniquely determined by the scalar addition of the components of the individual vectors. Orthogonal components are independent of each other because forces acting at ninety degrees to each other have no effect on the magnitude or direction of the other. Choosing a set of orthogonal basis vectors is often done by considering what set of basis vectors will make the mathematics most convenient. Choosing a basis vector that is in the same direction as one of the forces is desirable, since that force would then have only one non-zero component. Orthogonal force vectors can be three-dimensional with the third component being at right angles to the other two.
Equilibrium
When all the forces that act upon an object are balanced, then the object is said to be in a state of equilibrium. Hence, equilibrium occurs when the resultant force acting on a point particle is zero (that is, the vector sum of all forces is zero). When dealing with an extended body, it is also necessary that the net torque be zero. A body is in ''static equilibrium'' with respect to a frame of reference if it at rest and not accelerating, whereas a body in ''dynamic equilibrium'' is moving at a constant speed in a straight line, i.e., moving but not accelerating. What one observer sees as static equilibrium, another can see as dynamic equilibrium and vice versa.Static
Static equilibrium was understood well before the invention of classical mechanics. Objects that are not accelerating have zero net force acting on them. The simplest case of static equilibrium occurs when two forces are equal in magnitude but opposite in direction. For example, an object on a level surface is pulled (attracted) downward toward the center of the Earth by the force of gravity. At the same time, a force is applied by the surface that resists the downward force with equal upward force (called anormal force
In mechanics, the normal force F_n is the component of a contact force that is perpendicular to the surface that an object contacts. In this instance '' normal'' is used in the geometric sense and means perpendicular, as opposed to the meanin ...
). The situation produces zero net force and hence no acceleration.
Pushing against an object that rests on a frictional surface can result in a situation where the object does not move because the applied force is opposed by static friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
, generated between the object and the table surface. For a situation with no movement, the static friction force ''exactly'' balances the applied force resulting in no acceleration. The static friction increases or decreases in response to the applied force up to an upper limit determined by the characteristics of the contact between the surface and the object.
A static equilibrium between two forces is the most usual way of measuring forces, using simple devices such as weighing scale
A scale or balance is a device used to measure weight or mass. These are also known as mass scales, weight scales, mass balances, massometers, and weight balances.
The traditional scale consists of two plates or bowls suspended at equal d ...
s and spring balances. For example, an object suspended on a vertical spring scale
A spring scale, spring balance or newton meter is a type of mechanical force gauge or weighing scale. It consists of a Spring (device), spring fixed at one end with a hook to attach an object at the other. It works in accordance with Hooke's law ...
experiences the force of gravity acting on the object balanced by a force applied by the "spring reaction force", which equals the object's weight. Using such tools, some quantitative force laws were discovered: that the force of gravity is proportional to volume for objects of constant density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
(widely exploited for millennia to define standard weights); Archimedes' principle
Archimedes' principle states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fun ...
for buoyancy; Archimedes' analysis of the lever
A lever is a simple machine consisting of a beam (structure), beam or rigid rod pivoted at a fixed hinge, or '':wikt:fulcrum, fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, l ...
; Boyle's law
Boyle's law, also referred to as the Boyle–Mariotte law or Mariotte's law (especially in France), is an empirical gas laws, gas law that describes the relationship between pressure and volume of a confined gas. Boyle's law has been stated as:
...
for gas pressure; and Hooke's law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of ...
for springs. These were all formulated and experimentally verified before Isaac Newton expounded his three laws of motion.
Dynamic
 Dynamic equilibrium was first described by
Dynamic equilibrium was first described by Galileo
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642), commonly referred to as Galileo Galilei ( , , ) or mononymously as Galileo, was an Italian astronomer, physicist and engineer, sometimes described as a poly ...
who noticed that certain assumptions of Aristotelian physics were contradicted by observations and logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure o ...
. Galileo realized that simple velocity addition demands that the concept of an "absolute rest frame
In special relativity, the rest frame of a particle is the frame of reference (a coordinate system attached to physical markers) in which the particle is at rest.
The rest frame of compound objects (such as a fluid, or a solid made of many vibrati ...
" did not exist. Galileo concluded that motion in a constant velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
was completely equivalent to rest. This was contrary to Aristotle's notion of a "natural state" of rest that objects with mass naturally approached. Simple experiments showed that Galileo's understanding of the equivalence of constant velocity and rest were correct. For example, if a mariner dropped a cannonball from the crow's nest of a ship moving at a constant velocity, Aristotelian physics would have the cannonball fall straight down while the ship moved beneath it. Thus, in an Aristotelian universe, the falling cannonball would land behind the foot of the mast of a moving ship. When this experiment is actually conducted, the cannonball always falls at the foot of the mast, as if the cannonball knows to travel with the ship despite being separated from it. Since there is no forward horizontal force being applied on the cannonball as it falls, the only conclusion left is that the cannonball continues to move with the same velocity as the boat as it falls. Thus, no force is required to keep the cannonball moving at the constant forward velocity.
Moreover, any object traveling at a constant velocity must be subject to zero net force (resultant force). This is the definition of dynamic equilibrium: when all the forces on an object balance but it still moves at a constant velocity. A simple case of dynamic equilibrium occurs in constant velocity motion across a surface with kinetic friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
. In such a situation, a force is applied in the direction of motion while the kinetic friction force exactly opposes the applied force. This results in zero net force, but since the object started with a non-zero velocity, it continues to move with a non-zero velocity. Aristotle misinterpreted this motion as being caused by the applied force. When kinetic friction is taken into consideration it is clear that there is no net force causing constant velocity motion.
Examples of forces in classical mechanics
Some forces are consequences of the fundamental ones. In such situations, idealized models can be used to gain physical insight. For example, each solid object is considered arigid body
In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible, when a deforming pressure or deforming force is applied on it. The distance between any two given points on a rigid body rema ...
.
Gravitational force or Gravity
 What we now call gravity was not identified as a universal force until the work of Isaac Newton. Before Newton, the tendency for objects to fall towards the Earth was not understood to be related to the motions of celestial objects. Galileo was instrumental in describing the characteristics of falling objects by determining that the
What we now call gravity was not identified as a universal force until the work of Isaac Newton. Before Newton, the tendency for objects to fall towards the Earth was not understood to be related to the motions of celestial objects. Galileo was instrumental in describing the characteristics of falling objects by determining that the acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector ...
of every object in free-fall was constant and independent of the mass of the object. Today, this acceleration due to gravity towards the surface of the Earth is usually designated as and has a magnitude of about 9.81 meter
The metre (or meter in US spelling; symbol: m) is the base unit of length in the International System of Units (SI). Since 2019, the metre has been defined as the length of the path travelled by light in vacuum during a time interval of of ...
s per second squared (this measurement is taken from sea level and may vary depending on location), and points toward the center of the Earth. This observation means that the force of gravity on an object at the Earth's surface is directly proportional to the object's mass. Thus an object that has a mass of will experience a force:
For an object in free-fall, this force is unopposed and the net force on the object is its weight. For objects not in free-fall, the force of gravity is opposed by the reaction forces applied by their supports. For example, a person standing on the ground experiences zero net force, since a normal force
In mechanics, the normal force F_n is the component of a contact force that is perpendicular to the surface that an object contacts. In this instance '' normal'' is used in the geometric sense and means perpendicular, as opposed to the meanin ...
(a reaction force) is exerted by the ground upward on the person that counterbalances his weight that is directed downward.
Newton's contribution to gravitational theory was to unify the motions of heavenly bodies, which Aristotle had assumed were in a natural state of constant motion, with falling motion observed on the Earth. He proposed a law of gravity that could account for the celestial motions that had been described earlier using Kepler's laws of planetary motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler in 1609 (except the third law, which was fully published in 1619), describe the orbits of planets around the Sun. These laws replaced circular orbits and epicycles in ...
.
Newton came to realize that the effects of gravity might be observed in different ways at larger distances. In particular, Newton determined that the acceleration of the Moon around the Earth could be ascribed to the same force of gravity if the acceleration due to gravity decreased as an inverse square law
In science, an inverse-square law is any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cau ...
. Further, Newton realized that the acceleration of a body due to gravity is proportional to the mass of the other attracting body. Combining these ideas gives a formula that relates the mass () and the radius () of the Earth to the gravitational acceleration:
where the vector direction is given by , is the unit vector
In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ...
directed outward from the center of the Earth.
In this equation, a dimensional constant is used to describe the relative strength of gravity. This constant has come to be known as the Newtonian constant of gravitation
The gravitational constant is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's theory of general relativity. It is also known as t ...
, though its value was unknown in Newton's lifetime. Not until 1798 was Henry Cavendish
Henry Cavendish ( ; 10 October 1731 – 24 February 1810) was an English experimental and theoretical chemist and physicist. He is noted for his discovery of hydrogen, which he termed "inflammable air". He described the density of inflammable a ...
able to make the first measurement of using a torsion balance; this was widely reported in the press as a measurement of the mass of the Earth since knowing could allow one to solve for the Earth's mass given the above equation. Newton realized that since all celestial bodies followed the same laws of motion, his law of gravity had to be universal. Succinctly stated, Newton's law of gravitation
Newton's law of universal gravitation describes gravity as a force by stating that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the s ...
states that the force on a spherical object of mass due to the gravitational pull of mass is
where is the distance between the two objects' centers of mass and is the unit vector pointed in the direction away from the center of the first object toward the center of the second object.
This formula was powerful enough to stand as the basis for all subsequent descriptions of motion within the Solar System
The Solar SystemCapitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Sola ...
until the 20th century. During that time, sophisticated methods of perturbation analysis were invented to calculate the deviations of orbit
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an ...
s due to the influence of multiple bodies on a planet
A planet is a large, Hydrostatic equilibrium, rounded Astronomical object, astronomical body that is generally required to be in orbit around a star, stellar remnant, or brown dwarf, and is not one itself. The Solar System has eight planets b ...
, moon
The Moon is Earth's only natural satellite. It Orbit of the Moon, orbits around Earth at Lunar distance, an average distance of (; about 30 times Earth diameter, Earth's diameter). The Moon rotation, rotates, with a rotation period (lunar ...
, comet
A comet is an icy, small Solar System body that warms and begins to release gases when passing close to the Sun, a process called outgassing. This produces an extended, gravitationally unbound atmosphere or Coma (cometary), coma surrounding ...
, or asteroid
An asteroid is a minor planet—an object larger than a meteoroid that is neither a planet nor an identified comet—that orbits within the Solar System#Inner Solar System, inner Solar System or is co-orbital with Jupiter (Trojan asteroids). As ...
. The formalism was exact enough to allow mathematicians to predict the existence of the planet Neptune
Neptune is the eighth and farthest known planet from the Sun. It is the List of Solar System objects by size, fourth-largest planet in the Solar System by diameter, the third-most-massive planet, and the densest giant planet. It is 17 t ...
before it was observed.
Electromagnetic
The electrostatic force was first described in 1784 by Coulomb as a force that existed intrinsically between two charges. The properties of the electrostatic force were that it varied as aninverse square law
In science, an inverse-square law is any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cau ...
directed in the radial direction, was both attractive and repulsive (there was intrinsic polarity), was independent of the mass of the charged objects, and followed the superposition principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So th ...
. Coulomb's law
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental scientific law, law of physics that calculates the amount of force (physics), force between two electric charge, electrically charged particles at rest. This electric for ...
unifies all these observations into one succinct statement.
Subsequent mathematicians and physicists found the construct of the ''electric field
An electric field (sometimes called E-field) is a field (physics), physical field that surrounds electrically charged particles such as electrons. In classical electromagnetism, the electric field of a single charge (or group of charges) descri ...
'' to be useful for determining the electrostatic force on an electric charge at any point in space. The electric field was based on using a hypothetical "test charge In physical theories, a test particle, or test charge, is an idealized model of an object whose physical properties (usually mass, charge, or size) are assumed to be negligible except for the property being studied, which is considered to be insuf ...
" anywhere in space and then using Coulomb's Law to determine the electrostatic force. Thus the electric field anywhere in space is defined as
where is the magnitude of the hypothetical test charge. Similarly, the idea of the ''magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
'' was introduced to express how magnets can influence one another at a distance. The Lorentz force law gives the force upon a body with charge due to electric and magnetic fields:
where is the electromagnetic force, is the electric field at the body's location, is the magnetic field, and is the velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
of the particle. The magnetic contribution to the Lorentz force is the cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
of the velocity vector with the magnetic field.
The origin of electric and magnetic fields would not be fully explained until 1864 when James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism an ...
unified a number of earlier theories into a set of 20 scalar equations, which were later reformulated into 4 vector equations by Oliver Heaviside
Oliver Heaviside ( ; 18 May 1850 – 3 February 1925) was an English mathematician and physicist who invented a new technique for solving differential equations (equivalent to the Laplace transform), independently developed vector calculus, an ...
and Josiah Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American mechanical engineer and scientist who made fundamental theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynami ...
. These "Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, Electrical network, electr ...
" fully described the sources of the fields as being stationary and moving charges, and the interactions of the fields themselves. This led Maxwell to discover that electric and magnetic fields could be "self-generating" through a wave
In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance (change from List of types of equilibrium, equilibrium) of one or more quantities. ''Periodic waves'' oscillate repeatedly about an equilibrium ...
that traveled at a speed that he calculated to be the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
. This insight united the nascent fields of electromagnetic theory with optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
and led directly to a complete description of the electromagnetic spectrum
The electromagnetic spectrum is the full range of electromagnetic radiation, organized by frequency or wavelength. The spectrum is divided into separate bands, with different names for the electromagnetic waves within each band. From low to high ...
.
Normal
Friction
Friction is a force that opposes relative motion of two bodies. At the macroscopic scale, the frictional force is directly related to the normal force at the point of contact. There are two broad classifications of frictional forces:static friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
and kinetic friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
.
The static friction force () will exactly oppose forces applied to an object parallel to a surface up to the limit specified by the coefficient of static friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
() multiplied by the normal force (). In other words, the magnitude of the static friction force satisfies the inequality:
The kinetic friction force () is typically independent of both the forces applied and the movement of the object. Thus, the magnitude of the force equals:
where is the coefficient of kinetic friction. The coefficient of kinetic friction is normally less than the coefficient of static friction.
Tension
Tension forces can be modeled using ideal strings that are massless, frictionless, unbreakable, and do not stretch. They can be combined with idealpulley
Sheave without a rope
A pulley is a wheel on an axle or shaft enabling a taut cable or belt passing over the wheel to move and change direction, or transfer power between itself and a shaft.
A pulley may have a groove or grooves between flan ...
s, which allow ideal strings to switch physical direction. Ideal strings transmit tension forces instantaneously in action–reaction pairs so that if two objects are connected by an ideal string, any force directed along the string by the first object is accompanied by a force directed along the string in the opposite direction by the second object. By connecting the same string multiple times to the same object through the use of a configuration that uses movable pulleys, the tension force on a load can be multiplied. For every string that acts on a load, another factor of the tension force in the string acts on the load. Such machines allow a mechanical advantage for a corresponding increase in the length of displaced string needed to move the load. These tandem effects result ultimately in the conservation of mechanical energy since the work done on the load is the same no matter how complicated the machine.
Spring
 A simple elastic force acts to return a spring to its natural length. An ideal spring is taken to be massless, frictionless, unbreakable, and infinitely stretchable. Such springs exert forces that push when contracted, or pull when extended, in proportion to the
A simple elastic force acts to return a spring to its natural length. An ideal spring is taken to be massless, frictionless, unbreakable, and infinitely stretchable. Such springs exert forces that push when contracted, or pull when extended, in proportion to the displacement
Displacement may refer to:
Physical sciences
Mathematics and physics
*Displacement (geometry), is the difference between the final and initial position of a point trajectory (for instance, the center of mass of a moving object). The actual path ...
of the spring from its equilibrium position. This linear relationship was described by Robert Hooke
Robert Hooke (; 18 July 16353 March 1703) was an English polymath who was active as a physicist ("natural philosopher"), astronomer, geologist, meteorologist, and architect. He is credited as one of the first scientists to investigate living ...
in 1676, for whom Hooke's law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of ...
is named. If is the displacement, the force exerted by an ideal spring equals:
where is the spring constant (or force constant), which is particular to the spring. The minus sign accounts for the tendency of the force to act in opposition to the applied load.
Centripetal
For an object in uniform circular motion, the net force acting on the object equals: where is the mass of the object, is the velocity of the object and is the distance to the center of the circular path and is theunit vector
In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ...
pointing in the radial direction outwards from the center. This means that the net force felt by the object is always directed toward the center of the curving path. Such forces act perpendicular to the velocity vector associated with the motion of an object, and therefore do not change the speed
In kinematics, the speed (commonly referred to as ''v'') of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a non-negative scalar quantity. Intro ...
of the object (magnitude of the velocity), but only the direction of the velocity vector. More generally, the net force that accelerates an object can be resolved into a component that is perpendicular to the path, and one that is tangential to the path. This yields both the tangential force, which accelerates the object by either slowing it down or speeding it up, and the radial (centripetal) force, which changes its direction.
Continuum mechanics
point particle
A point particle, ideal particle or point-like particle (often spelled pointlike particle) is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension; being dimensionless, it does not take ...
s rather than three-dimensional objects. In real life, matter has extended structure and forces that act on one part of an object might affect other parts of an object. For situations where lattice holding together the atoms in an object is able to flow, contract, expand, or otherwise change shape, the theories of continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the deformation of and transmission of forces through materials modeled as a ''continuous medium'' (also called a ''continuum'') rather than as discrete particles.
Continuum mec ...
describe the way forces affect the material. For example, in extended fluids
In physics, a fluid is a liquid, gas, or other material that may continuously move and deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are substances which cannot res ...
, differences in pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
result in forces being directed along the pressure gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The g ...
s as follows:
where is the volume of the object in the fluid and is the scalar function that describes the pressure at all locations in space. Pressure gradients and differentials result in the buoyant force for fluids suspended in gravitational fields, winds in atmospheric science
Atmospheric science is the study of the Atmosphere of Earth, Earth's atmosphere and its various inner-working physical processes. Meteorology includes atmospheric chemistry and atmospheric physics with a major focus on weather forecasting. Clima ...
, and the lift associated with aerodynamics
Aerodynamics () is the study of the motion of atmosphere of Earth, air, particularly when affected by a solid object, such as an airplane wing. It involves topics covered in the field of fluid dynamics and its subfield of gas dynamics, and is an ...
and flight
Flight or flying is the motion (physics), motion of an Physical object, object through an atmosphere, or through the vacuum of Outer space, space, without contacting any planetary surface. This can be achieved by generating aerodynamic lift ass ...
.
A specific instance of such a force that is associated with dynamic pressure
In fluid dynamics, dynamic pressure (denoted by or and sometimes called velocity pressure) is the quantity defined by:Clancy, L.J., ''Aerodynamics'', Section 3.5
:q = \frac\rho\, u^2
where (in SI units):
* is the dynamic pressure in pascals ...
is fluid resistance: a body force that resists the motion of an object through a fluid due to viscosity
Viscosity is a measure of a fluid's rate-dependent drag (physics), resistance to a change in shape or to movement of its neighboring portions relative to one another. For liquids, it corresponds to the informal concept of ''thickness''; for e ...
. For so-called " Stokes' drag" the force is approximately proportional to the velocity, but opposite in direction:
where:
* is a constant that depends on the properties of the fluid and the dimensions of the object (usually the cross-sectional area), and
* is the velocity of the object.
More formally, forces in continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the deformation of and transmission of forces through materials modeled as a ''continuous medium'' (also called a ''continuum'') rather than as discrete particles.
Continuum mec ...
are fully described by a stress tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
with terms that are roughly defined as
where is the relevant cross-sectional area for the volume for which the stress tensor is being calculated. This formalism includes pressure terms associated with forces that act normal to the cross-sectional area (the matrix diagonals of the tensor) as well as shear terms associated with forces that act parallel to the cross-sectional area (the off-diagonal elements). The stress tensor accounts for forces that cause all strains (deformations) including also tensile stress
In continuum mechanics, stress is a physical quantity that describes forces present during deformation. For example, an object being pulled apart, such as a stretched elastic band, is subject to ''tensile'' stress and may undergo elongati ...
es and compressions.
Fictitious
There are forces that are frame dependent, meaning that they appear due to the adoption of non-Newtonian (that is, non-inertial) reference frames. Such forces include thecentrifugal force
Centrifugal force is a fictitious force in Newtonian mechanics (also called an "inertial" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It appears to be directed radially away from the axi ...
and the Coriolis force
In physics, the Coriolis force is a pseudo force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motio ...
. These forces are considered fictitious because they do not exist in frames of reference that are not accelerating. Because these forces are not genuine they are also referred to as "pseudo forces".
In general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
, gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
becomes a fictitious force that arises in situations where spacetime deviates from a flat geometry.
Concepts derived from force
Rotation and torque
 Forces that cause extended objects to rotate are associated with
Forces that cause extended objects to rotate are associated with torque
In physics and mechanics, torque is the rotational analogue of linear force. It is also referred to as the moment of force (also abbreviated to moment). The symbol for torque is typically \boldsymbol\tau, the lowercase Greek letter ''tau''. Wh ...
s. Mathematically, the torque of a force is defined relative to an arbitrary reference point as the cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
:
where is the position vector
In geometry, a position or position vector, also known as location vector or radius vector, is a Euclidean vector that represents a point ''P'' in space. Its length represents the distance in relation to an arbitrary reference origin ''O'', and ...
of the force application point relative to the reference point.
Torque is the rotation equivalent of force in the same way that angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
is the rotational equivalent for position
Position often refers to:
* Position (geometry), the spatial location (rather than orientation) of an entity
* Position, a job or occupation
Position may also refer to:
Games and recreation
* Position (poker), location relative to the dealer
* ...
, angular velocity
In physics, angular velocity (symbol or \vec, the lowercase Greek letter omega), also known as the angular frequency vector,(UP1) is a pseudovector representation of how the angular position or orientation of an object changes with time, i ...
for velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
, and angular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
for momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
. As a consequence of Newton's first law of motion, there exists rotational inertia
The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is defined relatively to a rotational axis. It is the ratio between ...
that ensures that all bodies maintain their angular momentum unless acted upon by an unbalanced torque. Likewise, Newton's second law of motion can be used to derive an analogous equation for the instantaneous angular acceleration
In physics, angular acceleration (symbol α, alpha) is the time rate of change of angular velocity. Following the two types of angular velocity, ''spin angular velocity'' and ''orbital angular velocity'', the respective types of angular accele ...
of the rigid body:
where
* is the moment of inertia
The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is defined relatively to a rotational axis. It is the ratio between ...
of the body
* is the angular acceleration of the body.
This provides a definition for the moment of inertia, which is the rotational equivalent for mass. In more advanced treatments of mechanics, where the rotation over a time interval is described, the moment of inertia must be substituted by the tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
that, when properly analyzed, fully determines the characteristics of rotations including precession
Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the first Euler angle, whereas the third Euler angle defines the rotation itself. In o ...
and nutation.
Equivalently, the differential form of Newton's second law provides an alternative definition of torque:
where is the angular momentum of the particle.
Newton's third law of motion requires that all objects exerting torques themselves experience equal and opposite torques, and therefore also directly implies the conservation of angular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
for closed systems that experience rotations and revolution
In political science, a revolution (, 'a turn around') is a rapid, fundamental transformation of a society's class, state, ethnic or religious structures. According to sociologist Jack Goldstone, all revolutions contain "a common set of elements ...
s through the action of internal torques.
Yank
The yank is defined as the rate of change of force : The term is used in biomechanical analysis, athletic assessment and robotic control. The second ("tug"), third ("snatch"), fourth ("shake"), and higher derivatives are rarely used.Kinematic integrals
Forces can be used to define a number of physical concepts by integrating with respect to kinematic variables. For example, integrating with respect to time gives the definition of impulse: which by Newton's second law must be equivalent to the change in momentum (yielding theImpulse momentum theorem
In classical mechanics, impulse (symbolized by or Imp) is the change in momentum of an object. If the initial momentum of an object is , and a subsequent momentum is , the object has received an impulse :
\mathbf=\mathbf_2 - \mathbf_1.
Moment ...
).
Similarly, integrating with respect to position gives a definition for the work done
In science, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, for a constant force aligned with the direction of motion, the work equals the product of the force stren ...
by a force:
which is equivalent to changes in kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
(yielding the work energy theorem).
Power ''P'' is the rate of change d''W''/d''t'' of the work ''W'', as the trajectory
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete tra ...
is extended by a position change in a time interval d''t'':
so
with the velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
.
Potential energy
Instead of a force, often the mathematically related concept of apotential energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity ...
field is used. For instance, the gravitational force acting upon an object can be seen as the action of the gravitational field
In physics, a gravitational field or gravitational acceleration field is a vector field used to explain the influences that a body extends into the space around itself. A gravitational field is used to explain gravitational phenomena, such as ...
that is present at the object's location. Restating mathematically the definition of energy (via the definition of work
Work may refer to:
* Work (human activity), intentional activity people perform to support themselves, others, or the community
** Manual labour, physical work done by humans
** House work, housework, or homemaking
** Working animal, an ani ...
), a potential scalar field
In mathematics and physics, a scalar field is a function associating a single number to each point in a region of space – possibly physical space. The scalar may either be a pure mathematical number ( dimensionless) or a scalar physical ...
is defined as that field whose gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The g ...
is equal and opposite to the force produced at every point:
Forces can be classified as conservative
Conservatism is a cultural, social, and political philosophy and ideology that seeks to promote and preserve traditional institutions, customs, and values. The central tenets of conservatism may vary in relation to the culture and civiliza ...
or nonconservative. Conservative forces are equivalent to the gradient of a potential
Potential generally refers to a currently unrealized ability. The term is used in a wide variety of fields, from physics to the social sciences to indicate things that are in a state where they are able to change in ways ranging from the simple r ...
while nonconservative forces are not.
Conservation
A conservative force that acts on aclosed system
A closed system is a natural physical system that does not allow transfer of matter in or out of the system, althoughin the contexts of physics, chemistry, engineering, etc.the transfer of energy (e.g. as work or heat) is allowed.
Physics
In cl ...
has an associated mechanical work that allows energy to convert only between kinetic or potential
Potential generally refers to a currently unrealized ability. The term is used in a wide variety of fields, from physics to the social sciences to indicate things that are in a state where they are able to change in ways ranging from the simple r ...
forms. This means that for a closed system, the net mechanical energy
In physical sciences, mechanical energy is the sum of macroscopic potential and kinetic energies. The principle of conservation of mechanical energy states that if an isolated system is subject only to conservative forces, then the mechanical ...
is conserved whenever a conservative force acts on the system. The force, therefore, is related directly to the difference in potential energy between two different locations in space, and can be considered to be an artifact of the potential field in the same way that the direction and amount of a flow of water can be considered to be an artifact of the contour map of the elevation of an area.
Conservative forces include gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
, the electromagnetic
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interacti ...
force, and the spring force. Each of these forces has models that are dependent on a position often given as a radial vector emanating from spherically symmetric potentials. Examples of this follow:
For gravity:
where is the gravitational constant
The gravitational constant is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's general relativity, theory of general relativity. It ...
, and is the mass of object ''n''.
For electrostatic forces:
where is electric permittivity of free space, and is the electric charge
Electric charge (symbol ''q'', sometimes ''Q'') is a physical property of matter that causes it to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative''. Like charges repel each other and ...
of object ''n''.
For spring forces:
where is the spring constant
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring (device), spring by some distance () Proportionality (mathematics)#Direct_proportionality, scales linearly with respect to that ...
.
For certain physical scenarios, it is impossible to model forces as being due to a simple gradient of potentials. This is often due a macroscopic statistical average of microstates
A microstate or ministate is a sovereign state having a very small population or land area, usually both. However, the meanings of "state" and "very small" are not well-defined in international law. Some recent attempts to define microstates ...
. For example, static friction is caused by the gradients of numerous electrostatic potentials between the atom
Atoms are the basic particles of the chemical elements. An atom consists of a atomic nucleus, nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished fr ...
s, but manifests as a force model that is independent of any macroscale position vector. Nonconservative forces other than friction include other contact force
A contact force is any force that occurs because of two objects making contact with each other. Contact forces are very common and are responsible for most visible interactions between macroscopic
The macroscopic scale is the length scale on ...
s, tension, compression, and drag. For any sufficiently detailed description, all these forces are the results of conservative ones since each of these macroscopic forces are the net results of the gradients of microscopic potentials.
The connection between macroscopic nonconservative forces and microscopic conservative forces is described by detailed treatment with statistical mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applicati ...
. In macroscopic closed systems, nonconservative forces act to change the internal energies of the system, and are often associated with the transfer of heat. According to the Second law of thermodynamics
The second law of thermodynamics is a physical law based on Universal (metaphysics), universal empirical observation concerning heat and Energy transformation, energy interconversions. A simple statement of the law is that heat always flows spont ...
, nonconservative forces necessarily result in energy transformations within closed systems from ordered to more random conditions as entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
increases.
Units
The SI unit of force is the newton (symbol N), which is the force required to accelerate a one kilogram mass at a rate of one meter per second squared, or kg·m·s−2.The corresponding CGS unit is thedyne
The dyne (symbol: dyn; ) is a derived units of measurement, unit of force (physics), force specified in the centimetre–gram–second system of units, centimetre–gram–second (CGS) system of units, a predecessor of the modern International S ...
, the force required to accelerate a one gram mass by one centimeter per second squared, or g·cm·s−2. A newton is thus equal to 100,000 dynes.
The gravitational foot-pound-second English unit
English units were the units of measurement used in England up to 1826 (when they were replaced by Imperial units), which evolved as a combination of the Anglo-Saxon and Roman systems of units. Various standards have applied to English units at ...
of force is the pound-force
The pound of force or pound-force (symbol: lbf, sometimes lbf,) is a unit of force used in some systems of measurement, including English Engineering units and the foot–pound–second system.
Pound-force should not be confused with poun ...
(lbf), defined as the force exerted by gravity on a pound-mass in the standard gravitational field of 9.80665 m·s−2. The pound-force provides an alternative unit of mass: one slug
Slug, or land slug, is a common name for any apparently shell-less Terrestrial mollusc, terrestrial gastropod mollusc. The word ''slug'' is also often used as part of the common name of any gastropod mollusc that has no shell, a very reduced ...
is the mass that will accelerate by one foot per second squared when acted on by one pound-force. An alternative unit of force in a different foot–pound–second system, the absolute fps system, is the poundal, defined as the force required to accelerate a one-pound mass at a rate of one foot per second squared.
The pound-force has a metric counterpart, less commonly used than the newton: the kilogram-force
The kilogram-force (kgf or kgF), or kilopond (kp, from ), is a non-standard Gravitational metric system, gravitational metric unit of force. It is not accepted for use with the International System of Units (SI) and is deprecated for most uses. T ...
(kgf) (sometimes kilopond), is the force exerted by standard gravity on one kilogram of mass. The kilogram-force leads to an alternate, but rarely used unit of mass: the metric slug (sometimes mug or hyl) is that mass that accelerates at 1 m·s−2 when subjected to a force of 1 kgf. The kilogram-force is not a part of the modern SI system, and is generally deprecated, sometimes used for expressing aircraft weight, jet thrust, bicycle spoke tension, torque wrench settings and engine output torque.
: See also '' Ton-force''.
Revisions of the force concept
At the beginning of the 20th century, new physical ideas emerged to explain experimental results in astronomical and submicroscopic realms. As discussed below, relativity alters the definition of momentum and quantum mechanics reuses the concept of "force" in microscopic contexts where Newton's laws do not apply directly.Special theory of relativity
In thespecial theory of relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between space and time. In Albert Einstein's 1905 paper,
"On the Electrodynamics of Moving Bodies", the theory is presen ...
, mass and energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
are equivalent (as can be seen by calculating the work required to accelerate an object). When an object's velocity increases, so does its energy and hence its mass equivalent (inertia). It thus requires more force to accelerate it the same amount than it did at a lower velocity. Newton's second law,
remains valid because it is a mathematical definition. But for momentum to be conserved at relativistic relative velocity, , momentum must be redefined as:
where is the rest mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, ...
and the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
.
The expression relating force and acceleration for a particle with constant non-zero rest mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, ...
moving in the direction at velocity is:
where
is called the Lorentz factor
The Lorentz factor or Lorentz term (also known as the gamma factor) is a dimensionless quantity expressing how much the measurements of time, length, and other physical properties change for an object while it moves. The expression appears in sev ...
. The Lorentz factor increases steeply as the relative velocity approaches the speed of light. Consequently, the greater and greater force must be applied to produce the same acceleration at extreme velocity. The relative velocity cannot reach .
If is very small compared to , then is very close to 1 and
is a close approximation. Even for use in relativity, one can restore the form of
through the use of four-vectors
In special relativity, a four-vector (or 4-vector, sometimes Lorentz vector) is an object with four components, which transform in a specific way under Lorentz transformations. Specifically, a four-vector is an element of a four-dimensional vect ...
. This relation is correct in relativity when is the four-force, is the invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, ...
, and is the four-acceleration.
The ''general'' theory of relativity incorporates a more radical departure from the Newtonian way of thinking about force, specifically gravitational force. This reimagining of the nature of gravity is described more fully below.
Quantum mechanics
Quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
is a theory of physics originally developed in order to understand microscopic phenomena: behavior at the scale of molecules, atoms or subatomic particles. Generally and loosely speaking, the smaller a system is, the more an adequate mathematical model will require understanding quantum effects. The conceptual underpinning of quantum physics is different from that of classical physics. Instead of thinking about quantities like position, momentum, and energy as properties that an object ''has'', one considers what result might ''appear'' when a measurement
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events.
In other words, measurement is a process of determining how large or small a physical quantity is as compared to ...
of a chosen type is performed. Quantum mechanics allows the physicist to calculate the probability that a chosen measurement will elicit a particular result. The expectation value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first moment) is a generalization of the weighted average. Informally, the expected va ...
for a measurement is the average of the possible results it might yield, weighted by their probabilities of occurrence.
In quantum mechanics, interactions are typically described in terms of energy rather than force. The Ehrenfest theorem
The Ehrenfest theorem, named after Austrian theoretical physicist Paul Ehrenfest, relates the time derivative of the expectation values of the position and momentum operators ''x'' and ''p'' to the expectation value of the force F=-V'(x) on a m ...
provides a connection between quantum expectation values and the classical concept of force, a connection that is necessarily inexact, as quantum physics is fundamentally different from classical. In quantum physics, the Born rule
The Born rule is a postulate of quantum mechanics that gives the probability that a measurement of a quantum system will yield a given result. In one commonly used application, it states that the probability density for finding a particle at a ...
is used to calculate the expectation values of a position measurement or a momentum measurement. These expectation values will generally change over time; that is, depending on the time at which (for example) a position measurement is performed, the probabilities for its different possible outcomes will vary. The Ehrenfest theorem says, roughly speaking, that the equations describing how these expectation values change over time have a form reminiscent of Newton's second law, with a force defined as the negative derivative of the potential energy. However, the more pronounced quantum effects are in a given situation, the more difficult it is to derive meaningful conclusions from this resemblance.
Quantum mechanics also introduces two new constraints that interact with forces at the submicroscopic scale and which are especially important for atoms. Despite the strong attraction of the nucleus, the uncertainty principle
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position a ...
limits the minimum extent of an electron probability distribution and the Pauli exclusion principle
In quantum mechanics, the Pauli exclusion principle (German: Pauli-Ausschlussprinzip) states that two or more identical particles with half-integer spins (i.e. fermions) cannot simultaneously occupy the same quantum state within a system that o ...
prevents electrons from sharing the same probability distribution. This gives rise to an emergent pressure known as degeneracy pressure
In astrophysics and condensed matter physics, electron degeneracy pressure is a quantum mechanical effect critical to understanding the stability of white dwarf stars and metal solids. It is a manifestation of the more general phenomenon of quan ...
. The dynamic equilibrium between the degeneracy pressure and the attractive electromagnetic force give atoms, molecules, liquids, and solids stability
Stability may refer to:
Mathematics
*Stability theory, the study of the stability of solutions to differential equations and dynamical systems
** Asymptotic stability
** Exponential stability
** Linear stability
**Lyapunov stability
** Marginal s ...
.
Quantum field theory
particle physics
Particle physics or high-energy physics is the study of Elementary particle, fundamental particles and fundamental interaction, forces that constitute matter and radiation. The field also studies combinations of elementary particles up to the s ...
, forces and the acceleration of particles are explained as a mathematical by-product of exchange of momentum-carrying gauge bosons. With the development of quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct phy ...
and general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
, it was realized that force is a redundant concept arising from conservation of momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
( 4-momentum in relativity and momentum of virtual particle
A virtual particle is a theoretical transient particle that exhibits some of the characteristics of an ordinary particle, while having its existence limited by the uncertainty principle, which allows the virtual particles to spontaneously emer ...
s in quantum electrodynamics
In particle physics, quantum electrodynamics (QED) is the Theory of relativity, relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quant ...
). The conservation of momentum can be directly derived from the homogeneity or symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
of space
Space is a three-dimensional continuum containing positions and directions. In classical physics, physical space is often conceived in three linear dimensions. Modern physicists usually consider it, with time, to be part of a boundless ...
and so is usually considered more fundamental than the concept of a force. Thus the currently known fundamental forces
In physics, the fundamental interactions or fundamental forces are interactions in nature that appear not to be reducible to more basic interactions. There are four fundamental interactions known to exist:
* gravity
* electromagnetism
* weak int ...
are considered more accurately to be "fundamental interactions
In physics, the fundamental interactions or fundamental forces are interactions in nature that appear not to be reducible to more basic interactions. There are four fundamental interactions known to exist:
* gravity
* electromagnetism
* weak int ...
".
While sophisticated mathematical descriptions are needed to predict, in full detail, the result of such interactions, there is a conceptually simple way to describe them through the use of Feynman diagram
In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced ...
s. In a Feynman diagram, each matter particle is represented as a straight line (see world line
The world line (or worldline) of an object is the path that an object traces in 4-dimensional spacetime. It is an important concept of modern physics, and particularly theoretical physics.
The concept of a "world line" is distinguished from c ...
) traveling through time, which normally increases up or to the right in the diagram. Matter and anti-matter particles are identical except for their direction of propagation through the Feynman diagram. World lines of particles intersect at interaction vertices, and the Feynman diagram represents any force arising from an interaction as occurring at the vertex with an associated instantaneous change in the direction of the particle world lines. Gauge bosons are emitted away from the vertex as wavy lines and, in the case of virtual particle exchange, are absorbed at an adjacent vertex. The utility of Feynman diagrams is that other types of physical phenomena that are part of the general picture of fundamental interaction
In physics, the fundamental interactions or fundamental forces are interactions in nature that appear not to be reducible to more basic interactions. There are four fundamental interactions known to exist:
* gravity
* electromagnetism
* weak int ...
s but are conceptually separate from forces can also be described using the same rules. For example, a Feynman diagram can describe in succinct detail how a neutron
The neutron is a subatomic particle, symbol or , that has no electric charge, and a mass slightly greater than that of a proton. The Discovery of the neutron, neutron was discovered by James Chadwick in 1932, leading to the discovery of nucle ...
decays into an electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary charge, elementary electric charge. It is a fundamental particle that comprises the ordinary matter that makes up the universe, along with up qua ...
, proton
A proton is a stable subatomic particle, symbol , Hydron (chemistry), H+, or 1H+ with a positive electric charge of +1 ''e'' (elementary charge). Its mass is slightly less than the mass of a neutron and approximately times the mass of an e ...
, and antineutrino
A neutrino ( ; denoted by the Greek letter ) is an elementary particle that interacts via the weak interaction and gravity. The neutrino is so named because it is electrically neutral and because its rest mass is so small ('' -ino'') that it ...
, an interaction mediated by the same gauge boson that is responsible for the weak nuclear force.
Fundamental interactions
All of the known forces of the universe are classified into fourfundamental interaction
In physics, the fundamental interactions or fundamental forces are interactions in nature that appear not to be reducible to more basic interactions. There are four fundamental interactions known to exist:
* gravity
* electromagnetism
* weak int ...
s. The strong and the weak forces act only at very short distances, and are responsible for the interactions between subatomic particle
In physics, a subatomic particle is a particle smaller than an atom. According to the Standard Model of particle physics, a subatomic particle can be either a composite particle, which is composed of other particles (for example, a baryon, lik ...
s, including nucleon
In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number.
Until the 1960s, nucleons were thought to be ele ...
s and compound nuclei. The electromagnetic force
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interac ...
acts between electric charge
Electric charge (symbol ''q'', sometimes ''Q'') is a physical property of matter that causes it to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative''. Like charges repel each other and ...
s, and the gravitational force
Newton's law of universal gravitation describes gravity as a force by stating that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the sq ...
acts between mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
es. All other forces in nature derive from these four fundamental interactions operating within quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, including the constraints introduced by the Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
and the Pauli exclusion principle
In quantum mechanics, the Pauli exclusion principle (German: Pauli-Ausschlussprinzip) states that two or more identical particles with half-integer spins (i.e. fermions) cannot simultaneously occupy the same quantum state within a system that o ...
. For example, friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
is a manifestation of the electromagnetic force acting between atoms
Atoms are the basic particles of the chemical elements. An atom consists of a nucleus of protons and generally neutrons, surrounded by an electromagnetically bound swarm of electrons. The chemical elements are distinguished from each other ...
of two surfaces. The forces in springs, modeled by Hooke's law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of ...
, are also the result of electromagnetic forces. Centrifugal forces are acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector ...
forces that arise simply from the acceleration of rotating frames of reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system, whose origin, orientation, and scale have been specified in physical space. It is based on a set of reference points, defined as geometric ...
.
The fundamental theories for forces developed from the unification of different ideas. For example, Newton's universal theory of gravitation
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
showed that the force responsible for objects falling near the surface of the Earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all ...
is also the force responsible for the falling of celestial bodies about the Earth (the Moon
The Moon is Earth's only natural satellite. It Orbit of the Moon, orbits around Earth at Lunar distance, an average distance of (; about 30 times Earth diameter, Earth's diameter). The Moon rotation, rotates, with a rotation period (lunar ...
) and around the Sun (the planets). Michael Faraday
Michael Faraday (; 22 September 1791 – 25 August 1867) was an English chemist and physicist who contributed to the study of electrochemistry and electromagnetism. His main discoveries include the principles underlying electromagnetic inducti ...
and James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism an ...
demonstrated that electric and magnetic forces were unified through a theory of electromagnetism. In the 20th century, the development of quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
led to a modern understanding that the first three fundamental forces (all except gravity) are manifestations of matter (fermion
In particle physics, a fermion is a subatomic particle that follows Fermi–Dirac statistics. Fermions have a half-integer spin (spin 1/2, spin , Spin (physics)#Higher spins, spin , etc.) and obey the Pauli exclusion principle. These particles i ...
s) interacting by exchanging virtual particle
A virtual particle is a theoretical transient particle that exhibits some of the characteristics of an ordinary particle, while having its existence limited by the uncertainty principle, which allows the virtual particles to spontaneously emer ...
s called gauge bosons. This Standard Model
The Standard Model of particle physics is the Scientific theory, theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions – excluding gravity) in the unive ...
of particle physics assumes a similarity between the forces and led scientists to predict the unification of the weak and electromagnetic forces in electroweak
In particle physics, the electroweak interaction or electroweak force is the unified description of two of the fundamental interactions of nature: electromagnetism (electromagnetic interaction) and the weak interaction. Although these two forc ...
theory, which was subsequently confirmed by observation.
Gravitational
 Newton's law of gravitation is an example of ''action at a distance'': one body, like the Sun, exerts an influence upon any other body, like the Earth, no matter how far apart they are. Moreover, this action at a distance is ''instantaneous.'' According to Newton's theory, the one body shifting position changes the gravitational pulls felt by all other bodies, all at the same instant of time.
Newton's law of gravitation is an example of ''action at a distance'': one body, like the Sun, exerts an influence upon any other body, like the Earth, no matter how far apart they are. Moreover, this action at a distance is ''instantaneous.'' According to Newton's theory, the one body shifting position changes the gravitational pulls felt by all other bodies, all at the same instant of time. Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
recognized that this was inconsistent with special relativity and its prediction that influences cannot travel faster than the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
. So, he sought a new theory of gravitation that would be relativistically consistent. Mercury's orbit did not match that predicted by Newton's law of gravitation. Some astrophysicists predicted the existence of an undiscovered planet ( Vulcan) that could explain the discrepancies. When Einstein formulated his theory of general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
(GR) he focused on Mercury's problematic orbit and found that his theory added a correction, which could account for the discrepancy. This was the first time that Newton's theory of gravity had been shown to be inexact.
Since then, general relativity has been acknowledged as the theory that best explains gravity. In GR, gravitation is not viewed as a force, but rather, objects moving freely in gravitational fields travel under their own inertia in straight lines through curved spacetime
In physics, curved spacetime is the mathematical model in which, with Einstein's theory of general relativity, gravity naturally arises, as opposed to being described as a fundamental force in Isaac Newton, Newton's static Euclidean reference fra ...
– defined as the shortest spacetime path between two spacetime events. From the perspective of the object, all motion occurs as if there were no gravitation whatsoever. It is only when observing the motion in a global sense that the curvature of spacetime can be observed and the force is inferred from the object's curved path. Thus, the straight line path in spacetime is seen as a curved line in space, and it is called the '' ballistic trajectory
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete tra ...
'' of the object. For example, a basketball
Basketball is a team sport in which two teams, most commonly of five players each, opposing one another on a rectangular Basketball court, court, compete with the primary objective of #Shooting, shooting a basketball (ball), basketball (appro ...
thrown from the ground moves in a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
, as it is in a uniform gravitational field. Its spacetime trajectory is almost a straight line, slightly curved (with the radius of curvature
In differential geometry, the radius of curvature, , is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius ...
of the order of few light-year
A light-year, alternatively spelled light year (ly or lyr), is a unit of length used to express astronomical distances and is equal to exactly , which is approximately 9.46 trillion km or 5.88 trillion mi. As defined by the International Astr ...
s). The time derivative of the changing momentum of the object is what we label as "gravitational force".
Electromagnetic
Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, Electrical network, electr ...
and the set of techniques built around them adequately describe a wide range of physics involving force in electricity and magnetism. This classical theory already includes relativity effects. Understanding quantized electromagnetic interactions between elementary particles requires quantum electrodynamics
In particle physics, quantum electrodynamics (QED) is the Theory of relativity, relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quant ...
(QED). In QED, photons are fundamental exchange particles, describing all interactions relating to electromagnetism including the electromagnetic force.
Strong nuclear
There are two "nuclear forces", which today are usually described as interactions that take place in quantum theories of particle physics. Thestrong nuclear force
In nuclear physics and particle physics, the strong interaction, also called the strong force or strong nuclear force, is one of the four known fundamental interactions. It confines quarks into protons, neutrons, and other hadron particles, an ...
is the force responsible for the structural integrity of atomic nuclei
The atomic nucleus is the small, dense region consisting of protons and neutrons at the center of an atom, discovered in 1911 by Ernest Rutherford at the University of Manchester based on the 1909 Geiger–Marsden gold foil experiment. Aft ...
, and gains its name from its ability to overpower the electromagnetic repulsion between protons.
The strong force is today understood to represent the interactions between quark
A quark () is a type of elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nucleus, atomic nuclei ...
s and gluon
A gluon ( ) is a type of Massless particle, massless elementary particle that mediates the strong interaction between quarks, acting as the exchange particle for the interaction. Gluons are massless vector bosons, thereby having a Spin (physi ...
s as detailed by the theory of quantum chromodynamics
In theoretical physics, quantum chromodynamics (QCD) is the study of the strong interaction between quarks mediated by gluons. Quarks are fundamental particles that make up composite hadrons such as the proton, neutron and pion. QCD is a type of ...
(QCD). The strong force is the fundamental force
In physics, the fundamental interactions or fundamental forces are interactions in nature that appear not to be reducible to more basic interactions. There are four fundamental interactions known to exist:
* gravity
* electromagnetism
* weak int ...
mediated by gluons, acting upon quarks, antiquarks, and the gluons themselves. The strong force only acts ''directly'' upon elementary particles. A residual is observed between hadron
In particle physics, a hadron is a composite subatomic particle made of two or more quarks held together by the strong nuclear force. Pronounced , the name is derived . They are analogous to molecules, which are held together by the electri ...
s (notably, the nucleon
In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number.
Until the 1960s, nucleons were thought to be ele ...
s in atomic nuclei), known as the nuclear force
The nuclear force (or nucleon–nucleon interaction, residual strong force, or, historically, strong nuclear force) is a force that acts between hadrons, most commonly observed between protons and neutrons of atoms. Neutrons and protons, both ...
. Here the strong force acts indirectly, transmitted as gluons that form part of the virtual pi and rho meson
In particle physics, a meson () is a type of hadronic subatomic particle composed of an equal number of quarks and antiquarks, usually one of each, bound together by the strong interaction. Because mesons are composed of quark subparticles, the ...
s, the classical transmitters of the nuclear force. The failure of many searches for free quarks has shown that the elementary particles affected are not directly observable. This phenomenon is called color confinement
In quantum chromodynamics (QCD), color confinement, often simply called confinement, is the phenomenon that color-charged particles (such as quarks and gluons) cannot be isolated, and therefore cannot be directly observed in normal conditions b ...
.
Weak nuclear
Unique among the fundamental interactions, the weak nuclear force creates no bound states. The weak force is due to the exchange of the heavyW and Z bosons
In particle physics, the W and Z bosons are vector bosons that are together known as the weak bosons or more generally as the intermediate vector bosons. These elementary particles mediate the weak interaction; the respective symbols are , , an ...
. Since the weak force is mediated by two types of bosons, it can be divided into two types of interaction or " vertices" — charged current, involving the electrically charged W+ and W− bosons, and neutral current
Weak neutral current interactions are one of the ways in which subatomic particles can interact by means of the weak force. These interactions are mediated by the Z boson. The discovery of weak neutral currents was a significant step towa ...
, involving electrically neutral Z0 bosons. The most familiar effect of weak interaction is beta decay
In nuclear physics, beta decay (β-decay) is a type of radioactive decay in which an atomic nucleus emits a beta particle (fast energetic electron or positron), transforming into an isobar of that nuclide. For example, beta decay of a neutron ...
(of neutrons in atomic nuclei) and the associated radioactivity
Radioactive decay (also known as nuclear decay, radioactivity, radioactive disintegration, or nuclear disintegration) is the process by which an unstable atomic nucleus loses energy by radiation. A material containing unstable nuclei is conside ...
. This is a type of charged-current interaction. The word "weak" derives from the fact that the field strength is some 1013 times less than that of the strong force
In nuclear physics and particle physics, the strong interaction, also called the strong force or strong nuclear force, is one of the four known fundamental interactions. It confines quarks into protons, neutrons, and other hadron particles, an ...
. Still, it is stronger than gravity over short distances. A consistent electroweak theory has also been developed, which shows that electromagnetic forces and the weak force are indistinguishable at a temperatures in excess of approximately . Such temperatures occurred in the plasma collisions in the early moments of the Big Bang
The Big Bang is a physical theory that describes how the universe expanded from an initial state of high density and temperature. Various cosmological models based on the Big Bang concept explain a broad range of phenomena, including th ...
.
See also
* * * * * * *References
External links
* * {{good article Natural philosophy Classical mechanics Vector physical quantities Temporal rates