|
Angular Velocity
In physics, angular velocity or rotational velocity ( or ), also known as angular frequency vector,(UP1) is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an object rotates or revolves relative to a point or axis). The magnitude of the pseudovector represents the ''angular speed'', the rate at which the object rotates or revolves, and its direction is normal to the instantaneous plane of rotation or angular displacement. The orientation of angular velocity is conventionally specified by the right-hand rule.(EM1) There are two types of angular velocity. * Orbital angular velocity refers to how fast a point object revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin. * Spin angular velocity refers to how fast a rigid body rotates with respect to its center of rotation and is independent of the choice of origin, in contrast to orbital angular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rigid Body
In physics, a rigid body (also known as a rigid object) is a solid body in which deformation is zero or so small it can be neglected. The distance between any two given points on a rigid body remains constant in time regardless of external forces or moments exerted on it. A rigid body is usually considered as a continuous distribution of mass. In the study of special relativity, a perfectly rigid body does not exist; and objects can only be assumed to be rigid if they are not moving near the speed of light. In quantum mechanics, a rigid body is usually thought of as a collection of point masses. For instance, molecules (consisting of the point masses: electrons and nuclei) are often seen as rigid bodies (see classification of molecules as rigid rotors). Kinematics Linear and angular position The position of a rigid body is the position of all the particles of which it is composed. To simplify the description of this position, we exploit the property that the body is r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that category was abolished in 1995). The radian is defined in the SI as being a dimensionless unit, with 1 rad = 1. Its symbol is accordingly often omitted, especially in mathematical writing. Definition One radian is defined as the angle subtended from the center of a circle which intercepts an arc equal in length to the radius of the circle. More generally, the magnitude in radians of a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, \theta = \frac, where is the subtended angle in radians, is arc length, and is radius. A right angle is exactly \frac radians. The rotation angle (360°) corresponding to one complete revolution is the length of the circumference divided by the radius, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics ( stress, elasticity, fluid mechanics, moment of inertia, ...), electrodynamics ( electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), general relativity (stress–energy tenso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position of an element (i.e., point). This is the informal meaning of the term dimension. In mathematics, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the -dimensional Euclidean space. When , this space is called three-dimensional Euclidean space (or simply Euclidean space when the context is clear). It serves as a model of the physical universe (when relativity theory is not considered), in which all known matter exists. While this space remains the most compelling and useful way to model the world as it is experienced, it is only one example of a large variety of spaces in three dimensions called 3-manifolds. In this classical example, when the t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Velocity
In physics, angular velocity or rotational velocity ( or ), also known as angular frequency vector,(UP1) is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an object rotates or revolves relative to a point or axis). The magnitude of the pseudovector represents the ''angular speed'', the rate at which the object rotates or revolves, and its direction is normal to the instantaneous plane of rotation or angular displacement. The orientation of angular velocity is conventionally specified by the right-hand rule.(EM1) There are two types of angular velocity. * Orbital angular velocity refers to how fast a point object revolves about a fixed origin, i.e. the time rate of change of its angular position relative to the origin. * Spin angular velocity refers to how fast a rigid body rotates with respect to its center of rotation and is independent of the choice of origin, in contrast to orbital angular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parity (physics)
In physics, a parity transformation (also called parity inversion) is the flip in the sign of ''one'' spatial coordinate. In three dimensions, it can also refer to the simultaneous flip in the sign of all three spatial coordinates (a point reflection): :\mathbf: \beginx\\y\\z\end \mapsto \begin-x\\-y\\-z\end. It can also be thought of as a test for chirality of a physical phenomenon, in that a parity inversion transforms a phenomenon into its mirror image. All fundamental interactions of elementary particles, with the exception of the weak interaction, are symmetric under parity. The weak interaction is chiral and thus provides a means for probing chirality in physics. In interactions that are symmetric under parity, such as electromagnetism in atomic and molecular physics, parity serves as a powerful controlling principle underlying quantum transitions. A matrix representation of P (in any number of dimensions) has determinant equal to −1, and hence is distinct from a rotati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudoscalar
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion while a true scalar does not. Any scalar product between a pseudovector and an ordinary vector is a pseudoscalar. The prototypical example of a pseudoscalar is the scalar triple product, which can be written as the scalar product between one of the vectors in the triple product and the cross product between the two other vectors, where the latter is a pseudovector. A pseudoscalar, when multiplied by an ordinary vector, becomes a pseudovector (axial vector); a similar construction creates the pseudotensor. Mathematically, a pseudoscalar is an element of the top exterior power of a vector space, or the top power of a Clifford algebra; see pseudoscalar (Clifford algebra). More generally, it is an element of the canonical bundle of a differentiable manifold. In physics In physics, a pseudoscalar denotes a physical quantity analogous to a scalar. Bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Vector
In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat"). The term ''direction vector'', commonly denoted as d, is used to describe a unit vector being used to represent spatial direction and relative direction. 2D spatial directions are numerically equivalent to points on the unit circle and spatial directions in 3D are equivalent to a point on the unit sphere. The normalized vector û of a non-zero vector u is the unit vector in the direction of u, i.e., :\mathbf = \frac where , u, is the norm (or length) of u. The term ''normalized vector'' is sometimes used as a synonym for ''unit vector''. Unit vectors are often chosen to form the basis of a vector space, and every vector in the space may be written as a linear combination of unit vectors. Orthogonal coordinates Cartesian coordinates Unit vectors may b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Coordinates
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the origin of a Cartesian coordinate system) is called the ''pole'', and the ray from the pole in the reference direction is the ''polar axis''. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. Angles in polar notation are generally expressed in either degrees or radians (2 rad being equal to 360°). Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concepts in the mid-17th century, though the actual term "polar coordinates" has been attributed to Gregorio Fontana in the 18th century. The initial motivation for the introduction of the polar system was the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Velocity1
Angular may refer to: Anatomy * Angular artery, the terminal part of the facial artery * Angular bone, a large bone in the lower jaw of amphibians and reptiles * Angular incisure, a small anatomical notch on the stomach * Angular gyrus, a region of the brain in the parietal lobe * Angular vein, formed by the junction of the frontal vein and supraorbital vein Other uses * Angular (web framework), an open-source web platform **AngularJS, the first incarnation of Angular * Angle, having an angle or angles * Angular diameter, describing how large a sphere or circle appears from a given point of view ** Angular diameter distance, used in astronomy * Angular Recording Corporation Angular Recording Corporation was an independent record label founded in New Cross, South East London. It was established in June 2003 by two ex- Goldsmiths College students, Joe Daniel and Joe Margetts, who reclaimed a local Ordnance Survey T ..., a British independent record label See also * Angle (dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can also be used for any other celestial body that is roughly spherical. In spatial (3D) geometry, as applied in astronomy, the equator of a rotating spheroid (such as a planet) is the parallel (circle of latitude) at which latitude is defined to be 0°. It is an imaginary line on the spheroid, equidistant from its poles, dividing it into northern and southern hemispheres. In other words, it is the intersection of the spheroid with the plane perpendicular to its axis of rotation and midway between its geographical poles. On and near the equator (on Earth), noontime sunlight appears almost directly overhead (no more than about 23° from the zenith) every day, year-round. Consequently, the equator has a rather stable daytime temperature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
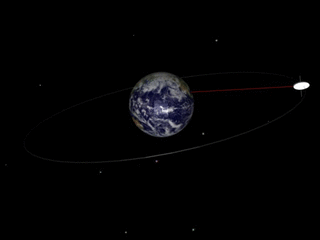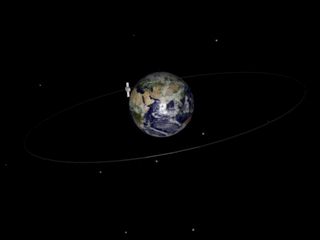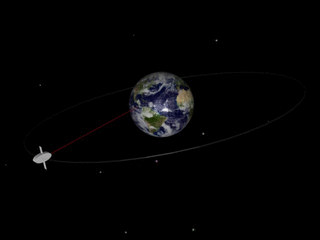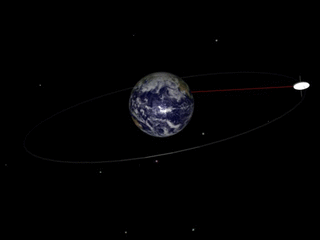
Geosynchronous Orbit
A geosynchronous orbit (sometimes abbreviated GSO) is an Earth-centered orbit with an orbital period that matches Earth's rotation on its axis, 23 hours, 56 minutes, and 4 seconds (one sidereal day). The synchronization of rotation and orbital period means that, for an observer on Earth's surface, an object in geosynchronous orbit returns to exactly the same position in the sky after a period of one sidereal day. Over the course of a day, the object's position in the sky may remain still or trace out a path, typically in a figure-8 form, whose precise characteristics depend on the orbit's inclination and eccentricity. A circular geosynchronous orbit has a constant altitude of . A special case of geosynchronous orbit is the geostationary orbit, which is a circular geosynchronous orbit in Earth's equatorial plane with both inclination and eccentricity equal to 0. A satellite in a geostationary orbit remains in the same position in the sky to observers on the surface. Comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |