|
Simple Machine
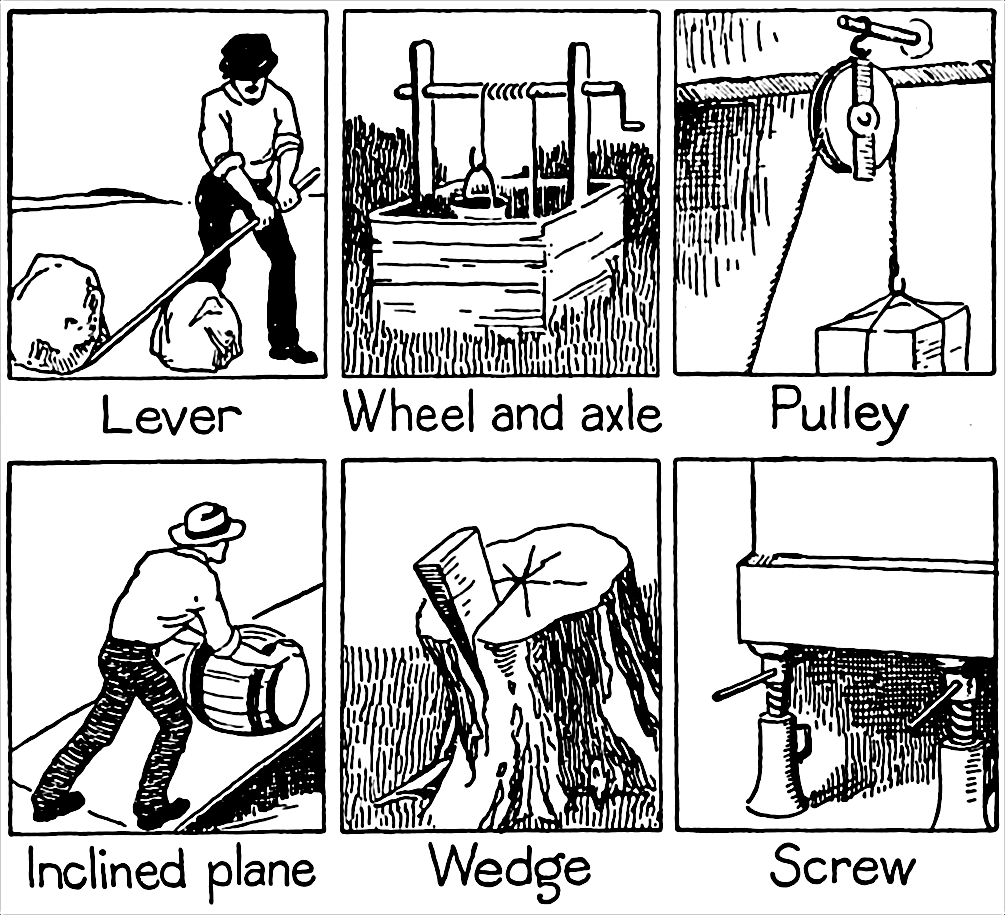
A simple machine is a machine, mechanical device that changes the Direction (geometry) , direction or Magnitude_(mathematics) , magnitude of a force. In general, they can be defined as the simplest Mechanism (engineering) , mechanisms that use mechanical advantage (also called leverage) to multiply force. Usually the term refers to the six classical simple machines that were defined by Renaissance scientists: * Lever * Wheel and axle * Pulley * Inclined plane * Wedge (mechanical device), Wedge * Screw (simple machine), Screw A simple machine uses a single applied force to do Mechanical work, work against a single load force. Ignoring friction losses, the work done on the load is equal to the work done by the applied force. The machine can increase the amount of the output force, at the cost of a proportional decrease in the distance moved by the load. The ratio of the output to the applied force is called the ''mechanical advantage''. Simple machines can be regarded as the eleme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Advantage
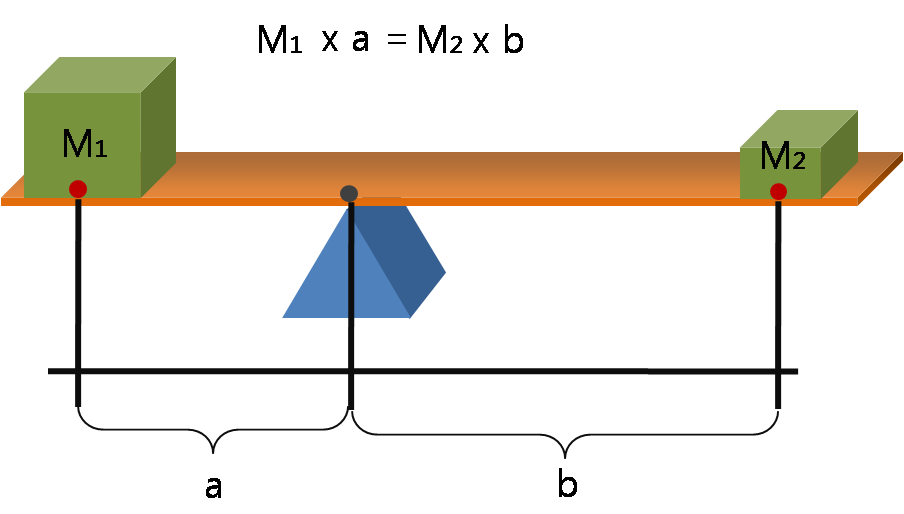
Mechanical advantage is a measure of the force amplification achieved by using a tool, mechanical device or machine system. The device trades off input forces against movement to obtain a desired amplification in the output force. The model for this is the ''law of the lever.'' Machine components designed to manage forces and movement in this way are called mechanisms. An ideal mechanism transmits power without adding to or subtracting from it. This means the ideal machine does not include a power source, is frictionless, and is constructed from rigid bodies that do not deflect or wear. The performance of a real system relative to this ideal is expressed in terms of efficiency factors that take into account departures from the ideal. Levers The lever is a movable bar that pivots on a fulcrum attached to or positioned on or across a fixed point. The lever operates by applying forces at different distances from the fulcrum, or pivot. The location of the fulcrum deter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inclined Plane
An inclined plane, also known as a ramp, is a flat supporting surface tilted at an angle from the vertical direction, with one end higher than the other, used as an aid for raising or lowering a load. The inclined plane is one of the six classical simple machines defined by Renaissance scientists. Inclined planes are used to move heavy loads over vertical obstacles. Examples vary from a ramp used to load goods into a truck, to a person walking up a pedestrian ramp, to an automobile or railroad train climbing a grade. Moving an object up an inclined plane requires less force than lifting it straight up, at a cost of an increase in the distance moved. The mechanical advantage of an inclined plane, the factor by which the force is reduced, is equal to the ratio of the length of the sloped surface to the height it spans. Owing to conservation of energy, the same amount of mechanical energy (work (physics), work) is required to lift a given object by a given vertical distance, disr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Six Mechanical Powers
6 (six) is the natural number following 5 and preceding 7. It is a composite number and the smallest perfect number. In mathematics A six-sided polygon is a hexagon, one of the three regular polygons capable of tiling the plane. A hexagon also has 6 edges as well as 6 internal and external angles. 6 is the second smallest composite number. It is also the first number that is the sum of its proper divisors, making it the smallest perfect number. It is also the only perfect number that doesn't have a digital root of 1. 6 is the first unitary perfect number, since it is the sum of its positive proper unitary divisors, without including itself. Only five such numbers are known to exist. 6 is the largest of the four all-Harshad numbers. 6 is the 2nd superior highly composite number, the 2nd colossally abundant number, the 3rd triangular number, the 4th highly composite number, a pronic number, a congruent number, a harmonic divisor number, and a semiprime. 6 is also the firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neoclassicism
Neoclassicism, also spelled Neo-classicism, emerged as a Western cultural movement in the decorative arts, decorative and visual arts, literature, theatre, music, and architecture that drew inspiration from the art and culture of classical antiquity. Neoclassicism was born in Rome, largely due to the writings of Johann Joachim Winckelmann during the rediscovery of Pompeii and Herculaneum. Its popularity expanded throughout Europe as a generation of European art students finished their Grand Tour and returned from Italy to their home countries with newly rediscovered Greco-Roman ideals. The main Neoclassical movement coincided with the 18th-century Age of Enlightenment, and continued into the early 19th century, eventually competing with Romanticism. In architecture, the style endured throughout the 19th, 20th, and into the 21st century. European Neoclassicism in the visual arts began in opposition to the then-dominant Rococo style. Rococo architecture emphasizes grace, Ornament ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lever
A lever is a simple machine consisting of a beam (structure), beam or rigid rod pivoted at a fixed hinge, or '':wikt:fulcrum, fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load, and effort, the lever is divided into Lever#Types of levers, three types. It is one of the six simple machines identified by Renaissance scientists. A lever amplifies an input force to provide a greater output force, which is said to provide leverage, which is mechanical advantage gained in the system, equal to the ratio of the output force to the input force. As such, the lever is a mechanical advantage device, trading off force against movement. Etymology The word "lever" entered English language, English around 1300 from . This sprang from the stem of the verb ''lever'', meaning "to raise". The verb, in turn, goes back to , itself from the adjective ''levis'', meaning "light" (as in "not heavy"). The word's primary origin is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heron Of Alexandria
Hero of Alexandria (; , , also known as Heron of Alexandria ; probably 1st or 2nd century AD) was a Greek mathematician and engineer who was active in Alexandria in Egypt during the Roman era. He has been described as the greatest experimentalist of antiquity and a representative of the Hellenistic scientific tradition. Hero published a well-recognized description of a steam-powered device called an ''aeolipile'', also known as "Hero's engine". Among his most famous inventions was a windwheel, constituting the earliest instance of wind harnessing on land. In his work ''Mechanics'', he described pantographs. Some of his ideas were derived from the works of Ctesibius. In mathematics, he wrote a commentary on Euclid's ''Elements'' and a work on applied geometry known as the ''Metrica''. He is mostly remembered for Heron's formula; a way to calculate the area of a triangle using only the lengths of its sides. Much of Hero's original writings and designs have been lost, but ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pappus Of Alexandria
Pappus of Alexandria (; ; AD) was a Greek mathematics, Greek mathematician of late antiquity known for his ''Synagoge'' (Συναγωγή) or ''Collection'' (), and for Pappus's hexagon theorem in projective geometry. Almost nothing is known about his life except for what can be found in his own writings, many of which are lost. Pappus apparently lived in Alexandria, where he worked as a Mathematics education, mathematics teacher to higher level students, one of whom was named Hermodorus.Pierre Dedron, J. Itard (1959) ''Mathematics And Mathematicians'', Vol. 1, p. 149 (trans. Judith V. Field) (Transworld Student Library, 1974) The ''Collection'', his best-known work, is a compendium of mathematics in eight volumes, the bulk of which survives. It covers a wide range of topics that were part of the ancient mathematics curriculum, including geometry, astronomy, and mechanics. Pappus was active in a period generally considered one of stagnation in mathematical studies, where, to s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristotelian Physics
Aristotelian physics is the form of natural philosophy described in the works of the Greek philosopher Aristotle (384–322 BC). In his work ''Physics'', Aristotle intended to establish general principles of change that govern all natural bodies, both living and inanimate, celestial and terrestrialincluding all motion (change with respect to place), quantitative change (change with respect to size or number), qualitative change, and substantial change (" coming to be" existence.html" ;"title="oming into existence">oming into existence, 'generation'or "passing away" [no longer existing, 'corruption']). To Aristotle, 'physics' was a broad field including subjects which would now be called the philosophy of mind, sensory experience, memory, anatomy and biology. It constitutes the foundation of the thought underlying many of his works. Key concepts of Aristotelian physics include the structuring of the cosmos into concentric spheres, with the Earth at the centre and celestial spher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenistic Sicily, Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and mathematical analysis, analysis by applying the concept of the Cavalieri's principle, infinitesimals and the method of exhaustion to derive and rigorously prove many geometry, geometrical theorem, theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Archimedes' other math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes Lever
Archimedes of Syracuse ( ; ) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and analysis by applying the concept of the infinitesimals and the method of exhaustion to derive and rigorously prove many geometrical theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Archimedes' other mathematical achievements include deriving an approximation of pi (), defining and investigating the Archimedean spiral, and devising a system using exponentiation for expr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematic Pair
In classical mechanics, a kinematic pair is a connection between two physical objects that imposes constraints on their relative movement (kinematics). German engineer Franz Reuleaux introduced the kinematic pair as a new approach to the study of machines that provided an advance over the notion of elements consisting of simple machines. Description Kinematics is the branch of classical mechanics which describes the motion of points, bodies (objects) and systems of bodies (groups of objects) without consideration of the causes of motion. Kinematics as a field of study is often referred to as the "geometry of motion". For further detail, see Kinematics. Hartenberg & Denavit presents the definition of a kinematic pair: In the matter of connections between rigid bodies, Reuleaux recognized two kinds; he called them higher and lower pairs (of elements). With higher pairs, the two elements are in contact at a point or along a line, as in a ball bearing or disk cam and follower; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |