|
Physics (Aristotle)
The ''Physics'' (Greek: Φυσικὴ ἀκρόασις ''Phusike akroasis''; Latin: ''Physica'', or ''Naturales Auscultationes'', possibly meaning " lectures on nature") is a named text, written in ancient Greek, collated from a collection of surviving manuscripts known as the Corpus Aristotelicum, attributed to the 4th-century BC philosopher Aristotle. The meaning of physics in Aristotle It is a collection of treatises or lessons that deals with the most general (philosophical) principles of natural or moving things, both living and non-living, rather than physical theories (in the modern sense) or investigations of the particular contents of the universe. The chief purpose of the work is to discover the principles and causes of (and not merely to describe) change, or movement, or motion (κίνησις ''kinesis''), especially that of natural wholes (mostly living things, but also inanimate wholes like the cosmos). In the conventional Andronicean ordering of Aristotle' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristotle Physica Page 1
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatetic school of philosophy within the Lyceum and the wider Aristotelian tradition. His writings cover many subjects including physics, biology, zoology, metaphysics, logic, ethics, aesthetics, poetry, theatre, music, rhetoric, psychology, linguistics, economics, politics, meteorology, geology, and government. Aristotle provided a complex synthesis of the various philosophies existing prior to him. It was above all from his teachings that the West inherited its intellectual lexicon, as well as problems and methods of inquiry. As a result, his philosophy has exerted a unique influence on almost every form of knowledge in the West and it continues to be a subject of contemporary philosophical discussion. Little is known about his life. Aristotle was born in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanistic Materialism
Mechanism is the belief that natural wholes (principally living things) are similar to complicated machines or artifacts, composed of parts lacking any intrinsic relationship to each other. The doctrine of mechanism in philosophy comes in two different flavors. They are both doctrines of metaphysics, but they are different in scope and ambitions: the first is a global doctrine about nature; the second is a local doctrine about humans and their minds, which is hotly contested. For clarity, we might distinguish these two doctrines as universal mechanism and anthropic mechanism. Universal mechanism The older doctrine, here called universal mechanism, is the ancient philosophies closely linked with materialism and reductionism, especially that of the atomists and to a large extent, stoic physics. They held that the universe is reducible to completely mechanical principles—that is, the motion and collision of matter. Later mechanists believed the achievements of the scient ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laws (dialogue)
The ''Laws'' (Greek: Νόμοι, ''Nómoi''; Latin: ''De Legibus'') is Plato's last and longest dialogue. The conversation depicted in the work's twelve books begins with the question of who is given the credit for establishing a civilization's laws. Its musings on the ethics of government and law have established it as a classic of political philosophy alongside Plato's more widely read '' Republic''. Scholars generally agree that Plato wrote this dialogue as an older man, having failed in his effort to guide the rule of the tyrant Dionysius I of Syracuse, instead having been thrown in prison. These events are alluded to in the '' Seventh Letter''. The text is noteworthy as Plato's only undisputed dialogue not to feature Socrates. Summary Setting Unlike most of Plato's dialogues, Socrates does not appear in the ''Laws'': the dialogue takes place on the island of Crete, and Socrates appears outside of Athens in Plato's writings only twice, in the ''Phaedrus'', where he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeno Of Elea
Zeno of Elea (; grc, Ζήνων ὁ Ἐλεᾱ́της; ) was a pre-Socratic Greek philosopher of Magna Graecia and a member of the Eleatic School founded by Parmenides. Aristotle called him the inventor of the dialectic. He is best known for his paradoxes, which Bertrand Russell described as "immeasurably subtle and profound". Life Little is known for certain about Zeno's life. Although written nearly a century after Zeno's death, the primary source of biographical information about Zeno is Plato's ''Parmenides (dialogue), Parmenides'' and he is also mentioned in Aristotle's ''Physics (Aristotle), Physics''. In the dialogue of ''Parmenides'', Plato describes a visit to Classical Athens, Athens by Zeno and Parmenides, at a time when Parmenides is "about 65", Zeno is "nearly 40", and Socrates is "a very young man".Plato, ''Parmenides'127b–e (at footnote n. 2) Assuming an age for Socrates of around 20 and taking the date of Socrates' birth as 469 BC gives an approximate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
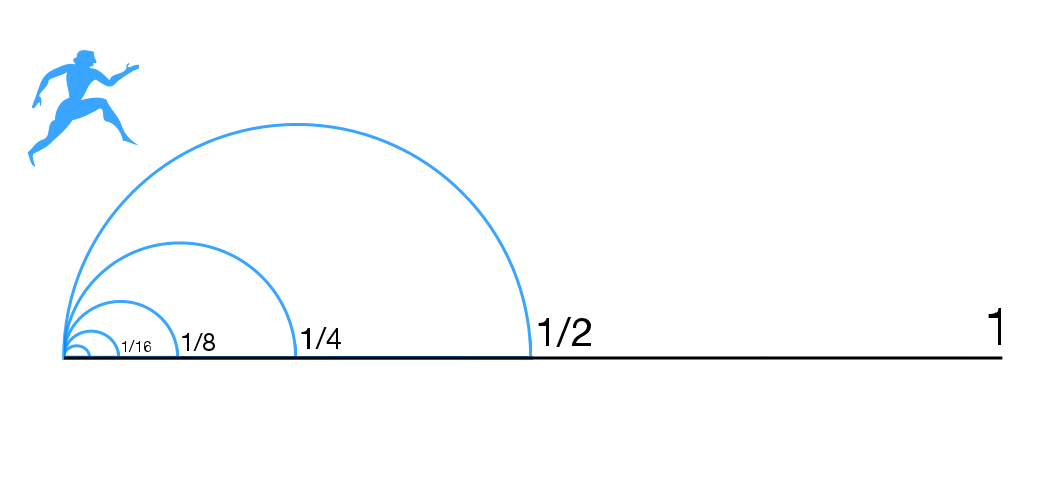
Zeno's Paradoxes
Zeno's paradoxes are a set of philosophical problems generally thought to have been devised by Greek philosopher Zeno of Elea (c. 490–430 BC) to support Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality and change is mistaken, and in particular that motion is nothing but an illusion. It is usually assumed, based on Plato's ''Parmenides'' (128a–d), that Zeno took on the project of creating these paradoxes because other philosophers had created paradoxes against Parmenides' view. Thus Plato has Zeno say the purpose of the paradoxes "is to show that their hypothesis that existences are many, if properly followed up, leads to still more absurd results than the hypothesis that they are one." Plato has Socrates claim that Zeno and Parmenides were essentially arguing exactly the same point. Some of Zeno's nine surviving paradoxes (preserved in Aristotle's ''Physics'' [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Mathematics
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous functions). Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (finite sets or sets with the same cardinality as the natural numbers). However, there is no exact definition of the term "discrete mathematics". The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometimes applied to parts of the field of discrete mathematics that deals with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
On Generation And Corruption
''On Generation and Corruption'' ( grc, Περὶ γενέσεως καὶ φθορᾶς; la, De Generatione et Corruptione), also known as ''On Coming to Be and Passing Away'' is a treatise by Aristotle. Like many of his texts, it is both scientific, part of Aristotle's biology, and philosophic. The philosophy is essentially empirical; as in all of Aristotle's works, the inferences made about the unexperienced and unobservable are based on observations and real experiences. Overview The question raised at the beginning of the text builds on an idea from Aristotle's earlier work '' The Physics''. Namely, whether things come into being through causes, through some prime material, or whether everything is generated purely through "alteration." Alteration concerned itself with the ability for elements to change based on common and uncommon qualities. From this important work Aristotle gives us two of his most remembered contributions. First, the Four Causes and also the F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Void (philosophy)
The Void is the philosophical concept of nothingness manifested. The notion of the Void is relevant to several realms of metaphysics. The Void is also prevalent in numerous facets of psychology, notably logotherapy. The manifestation of nothingness is closely associated with the contemplation of emptiness, and with human attempts to identify and personify it. As such, the concept of the Void, and ideas similar to it, have a significant and historically evolving presence in artistic and creative expression, as well as in academic, scientific and philosophical debate surrounding the nature of the human condition. In Western mystical traditions, it was often argued that the transcendent 'Ground of Being' could therefore be approached through aphairesis, a form of negation. Philosophy Western philosophers have discussed the existence and nature of void since Parmenides suggested it did not exist and used this to argue for the non-existence of change, motion, differentiation, among o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Actual Infinity
In the philosophy of mathematics, the abstraction of actual infinity involves the acceptance (if the axiom of infinity is included) of infinite entities as given, actual and completed objects. These might include the set of natural numbers, extended real numbers, transfinite numbers, or even an infinite sequence of rational numbers. Actual infinity is to be contrasted with potential infinity, in which a non-terminating process (such as "add 1 to the previous number") produces a sequence with no last element, and where each individual result is finite and is achieved in a finite number of steps. As a result, potential infinity is often formalized using the concept of limit. Anaximander The ancient Greek term for the potential or improper infinite was ''apeiron'' (unlimited or indefinite), in contrast to the actual or proper infinite ''aphorismenon''. ''Apeiron'' stands opposed to that which has a ''peras'' (limit). These notions are today denoted by ''potentially infinite'' an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potentiality And Actuality (Aristotle)
In philosophy, potentiality and actuality are a pair of closely connected principles which Aristotle used to analyze motion, causality, ethics, and physiology in his ''Physics'', ''Metaphysics'', '' Nicomachean Ethics'', and ''De Anima''. The concept of potentiality, in this context, generally refers to any "possibility" that a thing can be said to have. Aristotle did not consider all possibilities the same, and emphasized the importance of those that become real of their own accord when conditions are right and nothing stops them. Actuality, in contrast to potentiality, is the motion, change or activity that represents an exercise or fulfillment of a possibility, when a possibility becomes real in the fullest sense. These concepts, in modified forms, remained very important into the Middle Ages, influencing the development of medieval theology in several ways. In modern times the dichotomy has gradually lost importance, as understandings of nature and deity have changed. How ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Teleology
Teleology (from and )Partridge, Eric. 1977''Origins: A Short Etymological Dictionary of Modern English'' London: Routledge, p. 4187. or finalityDubray, Charles. 2020 912Teleology" In ''The Catholic Encyclopedia'' 14. New York: Robert Appleton Company. Retrieved 3 May 2020. – via '' New Advent'', transcribed by D. J. Potter is a reason or an explanation for something which serves as a function of its end, its purpose, or its goal, as opposed to something which serves as a function of its cause. A purpose that is imposed by human use, such as the purpose of a fork to hold food, is called '' extrinsic''. ''Natural teleology,'' common in classical philosophy, though controversial today, contends that natural entities also have ''intrinsic'' purposes, regardless of human use or opinion. For instance, Aristotle claimed that an acorn's intrinsic ''telos'' is to become a fully grown oak tree. Though ancient atomists rejected the notion of natural teleology, teleological accounts of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Telos (philosophy)
Telos (; ) is a term used by philosopher Aristotle to refer to the final cause of a natural organ or entity, or of a work of human art. Intentional actualization of potential or inherent purpose,"Telos.''Philosophy Terms'' Retrieved 3 May 2020. similar to the notion of an 'end goal' or ''. Moreover, it can be understood as the "supreme end of man's endeavour". ''Telos'' is the root of the modern term teleology, the study of purposiveness or of objects with a view to their aims, purposes, or intentions. Teleology is central in Aristotle's work on plant and animal biology, and human ethics, through his theory of the four causes. Aristotle's notion that everything has a ''telos'' also gave rise to epistemology. Applied to philosophical theories of history, it refers to a messianic redemption or some other utopia, such as postulated by Christian salvation history, or in the schools of thought of Georg Wilhelm Friedrich Hegel and Karl Marx. In general philosophy ''Telos'' has been ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |