Kullback–Leibler Divergence

In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted $D_\text(P \parallel Q)$, is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as

$D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text$

A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for certain classes of distributions (notably an exponential family), it satisfies a generalized Pythagorean theorem (which applies to squared distances).

Relative entropy is always a non-negative real number, with value 0 if and only if the two distributions in question are identical. It has diverse applications, both theoretical, such as characterizing the relative (Shannon) entropy in information systems, randomness in continuous time-series, and information gain when comparing statistical models of inference; and practical, such as applied statistics, fluid mechanics, neuroscience, bioinformatics, and machine learning.

Introduction and context

Consider two probability distributions and . Usually, represents the data, the observations, or a measured probability distribution. Distribution represents instead a theory, a model, a description or an approximation of . The Kullback–Leibler divergence $D_\text(P \parallel Q)$ is then interpreted as the average difference of the number of bits required for encoding samples of using a code optimized for rather than one optimized for . Note that the roles of and can be reversed in some situations where that is easier to compute, such as with the expectation–maximization algorithm (EM) and evidence lower bound (ELBO) computations.

Etymology

The relative entropy was introduced by Solomon Kullback and Richard Leibler in as "the mean information for discrimination between $H_1$ and $H_2$ per observation from $\mu_1$", where one is comparing two probability measures $\mu_1, \mu_2$, and $H_1, H_2$ are the hypotheses that one is selecting from measure $\mu_1, \mu_2$ (respectively). They denoted this by $I(1:2)$, and defined the "'divergence' between $\mu_1$ and $\mu_2$" as the symmetrized quantity $J(1,2) = I(1:2) + I(2:1)$, which had already been defined and used by Harold Jeffreys in 1948. In , the symmetrized form is again referred to as the "divergence", and the relative entropies in each direction are referred to as a "directed divergences" between two distributions; Kullback preferred the term discrimination information. The term "divergence" is in contrast to a distance (metric), since the symmetrized divergence does not satisfy the triangle inequality. Numerous references to earlier uses of the symmetrized divergence and to other statistical distances are given in . The asymmetric "directed divergence" has come to be known as the Kullback–Leibler divergence, while the symmetrized "divergence" is now referred to as the Jeffreys divergence.

Definition

For discrete probability distributions and defined on the same sample space, the relative entropy from to is defined to be

$D_\text(P \parallel Q) = \sum_ P(x) \, \log\frac\text$

which is equivalent to

$D_\text(P \parallel Q) = -\sum_ P(x) \, \log\frac\text$

In other words, it is the expectation of the logarithmic difference between the probabilities and , where the expectation is taken using the probabilities .

Relative entropy is only defined in this way if, for all , $Q(x) = 0$ implies $P(x) = 0$ (absolute continuity). Otherwise, it is often defined as but the value $\ +\infty\$ is possible even if $Q(x) \ne 0$ everywhere, provided that $\mathcal$ is infinite in extent. Analogous comments apply to the continuous and general measure cases defined below.

Whenever $P(x)$ is zero the contribution of the corresponding term is interpreted as zero because

$\lim_ x \, \log(x) = 0\text$

For distributions and of a continuous random variable, relative entropy is defined to be the integral

$D_\text(P \parallel Q) = \int_^\infty p(x) \, \log\frac \, dx\text$

where and denote the probability densities of and .

More generally, if and are probability measures on a measurable space $\mathcal\, ,$ and is absolutely continuous with respect to , then the relative entropy from to is defined as

$D_\text(P \parallel Q) = \int_ \log \frac \, P(dx)\text$

where $\frac$ is the Radon–Nikodym derivative of with respect to , i.e. the unique almost everywhere defined function on $\mathcal$ such that $P(dx) = r(x) Q(dx)$ which exists because is absolutely continuous with respect to . Also we assume the expression on the right-hand side exists. Equivalently (by the chain rule), this can be written as

$D_\text(P \parallel Q) = \int_ \frac\ \log\frac \ Q(dx)\text$

which is the entropy of relative to . Continuing in this case, if $\mu$ is any measure on $\mathcal$ for which densities and with $P(dx) = p(x) \mu(dx)$ and $Q(dx) = q(x) \mu(dx)$ exist (meaning that and are both absolutely continuous with respect to then the relative entropy from to is given as

$D_\text(P \parallel Q) = \int_ p(x)\, \log\frac \ \mu(dx)\text$

Note that such a measure $\mu$ for which densities can be defined always exists, since one can take $\mu = \frac \left( P + Q \right)$ although in practice it will usually be one that applies in the context such as counting measure for discrete distributions, or Lebesgue measure or a convenient variant thereof such as Gaussian measure or the uniform measure on the sphere, Haar measure on a Lie group etc. for continuous distributions.
The logarithms in these formulae are usually taken to base 2 if information is measured in units of bits, or to base if information is measured in nats. Most formulas involving relative entropy hold regardless of the base of the logarithm.

Various conventions exist for referring to $D_\text(P \parallel Q)$ in words. Often it is referred to as the divergence ''between'' and , but this fails to convey the fundamental asymmetry in the relation. Sometimes, as in this article, it may be described as the divergence of ''from'' or as the divergence ''from'' ''to'' . This reflects the asymmetry in Bayesian inference, which starts ''from'' a prior and updates ''to'' the posterior . Another common way to refer to $D_\text(P \parallel Q)$ is as the relative entropy of ''with respect to'' or the information gain from over .

Basic example

Kullback gives the following example (Table 2.1, Example 2.1). Let and be the distributions shown in the table and figure. is the distribution on the left side of the figure, a binomial distribution with $N = 2$ and $p = 0.4$. is the distribution on the right side of the figure, a discrete uniform distribution with the three possible outcomes (i.e. $\mathcal=\$), each with probability $p = 1/3$.

Relative entropies $D_\text(P \parallel Q)$ and $D_\text(Q \parallel P)$ are calculated as follows. This example uses the natural log with base , designated to get results in nats (see units of information):

$\begin D_\text(P \parallel Q) &= \sum_ P(x) \, \ln\frac \\ &= \frac \ln\frac + \frac \ln\frac + \frac \ln\frac \\ & = \frac \left(32 \ln 2 + 55 \ln 3 - 50 \ln 5 \right) \\ &\approx 0.0852996\text \end$

$\begin D_\text(Q \parallel P) &= \sum_ Q(x) \, \ln\frac \\ &= \frac \, \ln\frac + \frac \, \ln\frac + \frac \, \ln\frac \\ &= \frac \left(-4 \ln 2 - 6 \ln 3 + 6 \ln 5 \right) \\ &\approx 0.097455\text \end$

Interpretations

Statistics

In the field of statistics, the Neyman–Pearson lemma states that the most powerful way to distinguish between the two distributions and based on an observation (drawn from one of them) is through the log of the ratio of their likelihoods: $\log P(Y) - \log Q(Y)$. The KL divergence is the expected value of this statistic if is actually drawn from . Kullback motivated the statistic as an expected log likelihood ratio.

Coding

In the context of coding theory, $D_\text(P \parallel Q)$ can be constructed by measuring the expected number of extra bits required to code samples from using a code optimized for rather than the code optimized for .

Inference

In the context of machine learning, $D_\text(P \parallel Q)$ is often called the information gain achieved if would be used instead of which is currently used. By analogy with information theory, it is called the ''relative entropy'' of with respect to .

Expressed in the language of Bayesian inference, $D_\text(P \parallel Q)$ is a measure of the information gained by revising one's beliefs from the prior probability distribution to the posterior probability distribution . In other words, it is the amount of information lost when is used to approximate .

Information geometry

In applications, typically represents the "true" distribution of data, observations, or a precisely calculated theoretical distribution, while typically represents a theory, model, description, or approximation of . In order to find a distribution that is closest to , we can minimize the KL divergence and compute an information projection.

While it is a statistical distance, it is not a metric, the most familiar type of distance, but instead it is a divergence. While metrics are symmetric and generalize ''linear'' distance, satisfying the triangle inequality, divergences are asymmetric and generalize ''squared'' distance, in some cases satisfying a generalized Pythagorean theorem. In general $D_\text(P \parallel Q)$ does not equal $D_\text(Q \parallel P)$, and the asymmetry is an important part of the geometry. The infinitesimal form of relative entropy, specifically its Hessian, gives a metric tensor that equals the Fisher information metric; see . Fisher information metric on the certain probability distribution let determine the natural gradient for information-geometric optimization algorithms. Its quantum version is Fubini-study metric. Relative entropy satisfies a generalized Pythagorean theorem for exponential families (geometrically interpreted as dually flat manifolds), and this allows one to minimize relative entropy by geometric means, for example by information projection and in maximum likelihood estimation.

The relative entropy is the Bregman divergence generated by the negative entropy, but it is also of the form of an -divergence. For probabilities over a finite alphabet, it is unique in being a member of both of these classes of statistical divergences. The application of Bregman divergence can be found in mirror descent.

Finance (game theory)

Consider a growth-optimizing investor in a fair game with mutually exclusive outcomes
(e.g. a “horse race” in which the official odds add up to one).
The rate of return expected by such an investor is equal to the relative entropy
between the investor's believed probabilities and the official odds.
This is a special case of a much more general connection between financial returns and divergence measures.

Financial risks are connected to $D_ \text$ via information geometry. Investors' views, the prevailing market view, and risky scenarios form triangles on the relevant manifold of probability distributions. The shape of the triangles determines key financial risks (both qualitatively and quantitatively). For instance, obtuse triangles in which investors' views and risk scenarios appear on “opposite sides” relative to the market describe negative risks, acute triangles describe positive exposure, and the right-angled situation in the middle corresponds to zero risk. Extending this concept, relative entropy can be hypothetically utilised to identify the behaviour of informed investors, if one takes this to be represented by the magnitude and deviations away from the prior expectations of fund flows, for example.

Motivation

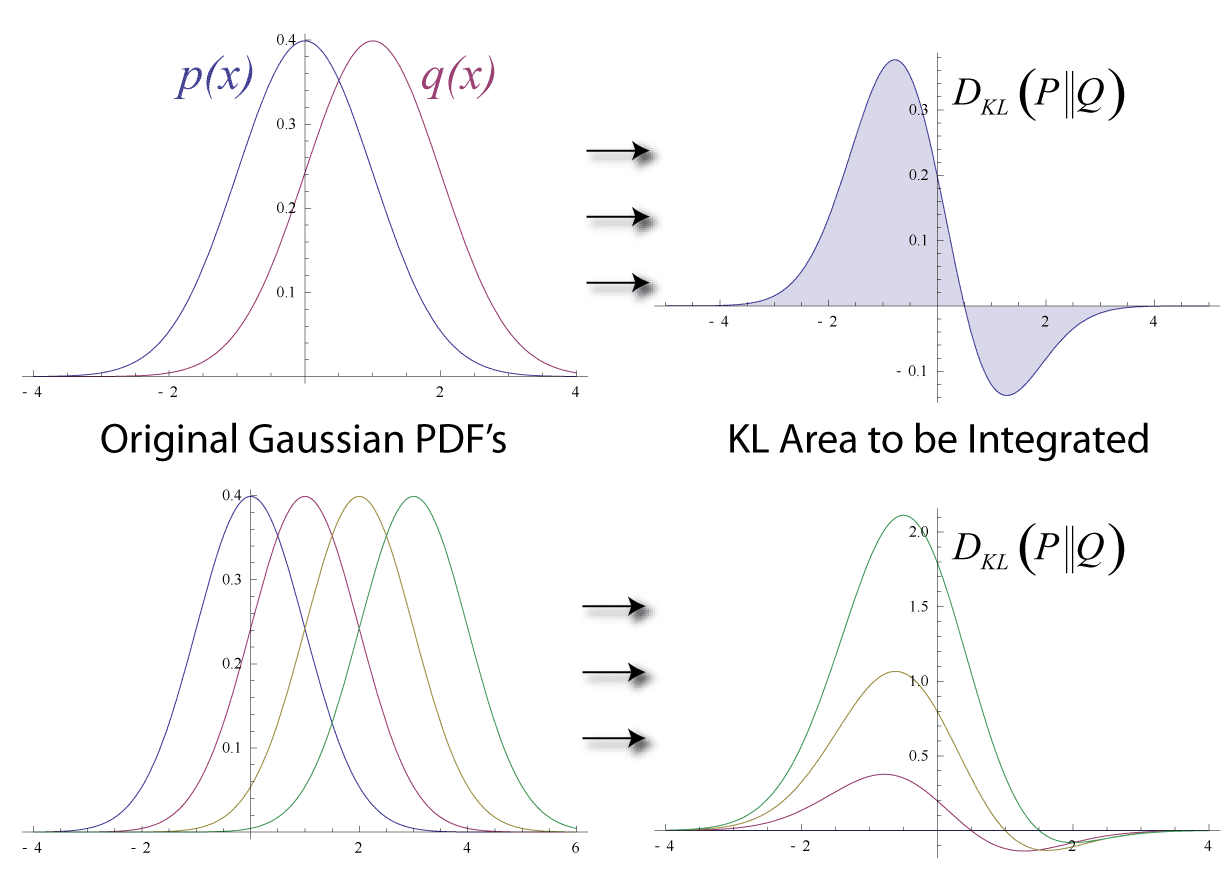
In information theory, the Kraft–McMillan theorem establishes that any directly decodable coding scheme for coding a message to identify one value $x_i$ out of a set of possibilities can be seen as representing an implicit probability distribution $q(x_i)=2^$ over , where $\ell_i$ is the length of the code for $x_i$ in bits. Therefore, relative entropy can be interpreted as the expected extra message-length per datum that must be communicated if a code that is optimal for a given (wrong) distribution is used, compared to using a code based on the true distribution : it is the ''excess'' entropy.

\begin
D_\text(P\parallel Q) &= \sum_ p(x) \log \frac - \sum_ p(x) \log \frac \\ pt &= \Eta(P, Q) - \Eta(P)
\end

where $\Eta(P,Q)$ is the cross entropy of relative to and $\Eta(P)$ is the entropy of (which is the same as the cross-entropy of P with itself).

The relative entropy $D_\text(P \parallel Q)$ can be thought of geometrically as a statistical distance, a measure of how far the distribution is from the distribution . Geometrically it is a divergence: an asymmetric, generalized form of squared distance. The cross-entropy $H(P,Q)$ is itself such a measurement (formally a loss function), but it cannot be thought of as a distance, since $H(P,P)=:H(P)$ is not zero. This can be fixed by subtracting $H(P)$ to make $D_\text(P \parallel Q)$ agree more closely with our notion of distance, as the ''excess'' loss. The resulting function is asymmetric, and while this can be symmetrized (see ), the asymmetric form is more useful. See for more on the geometric interpretation.

Relative entropy relates to " rate function" in the theory of large deviations.Novak S.Y. (2011), ''Extreme Value Methods with Applications to Finance'' ch. 14.5 ( Chapman & Hall). .

Arthur Hobson proved that relative entropy is the only measure of difference between probability distributions that satisfies some desired properties, which are the canonical extension to those appearing in a commonly used characterization of entropy. Consequently, mutual information is the only measure of mutual dependence that obeys certain related conditions, since it can be defined in terms of Kullback–Leibler divergence.

Properties

* Relative entropy is always non-negative, $D_\text(P \parallel Q) \geq 0,$ a result known as Gibbs' inequality, with $D_\text(P\parallel Q)$ equals zero if and only if $P = Q$ as measures.

In particular, if $P(dx) = p(x) \mu(dx)$ and $Q(dx) = q(x)\mu(dx)$, then $p(x) = q(x)$ $\mu$-almost everywhere. The entropy $\Eta(P)$ thus sets a minimum value for the cross-entropy $\Eta(P, Q)$, the expected number of bits required when using a code based on rather than ; and the Kullback–Leibler divergence therefore represents the expected number of extra bits that must be transmitted to identify a value drawn from , if a code is used corresponding to the probability distribution , rather than the "true" distribution .
* No upper-bound exists for the general case. However, it is shown that if and are two discrete probability distributions built by distributing the same discrete quantity, then the maximum value of $D_\text(P\parallel Q)$ can be calculated.
* Relative entropy remains well-defined for continuous distributions, and furthermore is invariant under parameter transformations. For example, if a transformation is made from variable to variable $y(x)$, then, since $P(dx) = p(x) \, dx = \tilde(y) \, dy = \tilde(y(x)) \left, \tfrac(x)\ \,dx$ and $Q(dx)= q(x)\, dx = \tilde(y) \, dy = \tilde(y) \left, \tfrac(x)\ dx$ where $\left, \tfrac(x)\$ is the absolute value of the derivative or more generally of the Jacobian, the relative entropy may be rewritten: \begin
D_\text(P \parallel Q)
&= \int_^ p(x) \, \log\frac \, dx \\ pt &= \int_^ \tilde(y(x)) \left, \frac\ \log\frac\, dx \\
&= \int_^ \tilde(y) \, \log\frac \, dy
\end where $y_a = y(x_a)$ and $y_b = y(x_b)$. Although it was assumed that the transformation was continuous, this need not be the case. This also shows that the relative entropy produces a dimensionally consistent quantity, since if is a dimensioned variable, $p(x)$ and $q(x)$ are also dimensioned, since e.g. $P(dx) = p(x) \, dx$ is dimensionless. The argument of the logarithmic term is and remains dimensionless, as it must. It can therefore be seen as in some ways a more fundamental quantity than some other properties in information theorySee the section "differential entropy – 4" i
Relative Entropy
video lecture by Sergio Verdú NIPS 2009 (such as self-information or Shannon entropy), which can become undefined or negative for non-discrete probabilities.
* Relative entropy is additive for independent distributions in much the same way as Shannon entropy. If $P_1, P_2$ are independent distributions, and $P(dx, dy) = P_1(dx)P_2(dy)$, and likewise $Q(dx, dy) = Q_1(dx)Q_2(dy)$ for independent distributions $Q_1, Q_2$ then $D_\text(P \parallel Q) = D_\text(P_1 \parallel Q_1) + D_\text(P_2 \parallel Q_2).$
* Relative entropy $D_\text(P \parallel Q)$ is convex in the pair of probability measures $(P,Q)$, i.e. if $(P_1,Q_1)$ and $(P_2,Q_2)$ are two pairs of probability measures then $D_\text(\lambda P_1 + (1 - \lambda) P_2 \parallel \lambda Q_1 + (1 - \lambda) Q_2) \le \lambda D_\text(P_1 \parallel Q_1) + (1 - \lambda)D_\text(P_2 \parallel Q_2) \text 0 \le \lambda \le 1.$
* $D_\text(P \parallel Q)$ may be Taylor expanded about its minimum (i.e. $P=Q$) as $D_\text(P \parallel Q) = \sum_^\infty \frac \sum_ \frac$ which converges if and only if $P \leq 2Q$ almost surely w.r.t $Q$.

Denote $f(\alpha) := D_\text((1-\alpha) Q + \alpha P \parallel Q)$ and note that $D_\text(P \parallel Q) = f(1)$. The first derivative of $f$ may be derived and evaluated as follows
$\begin f'(\alpha) &= \sum_ (P(x) - Q(x)) \left(\log\left(\frac\right) + 1\right) \\ &= \sum_ (P(x) - Q(x)) \log\left(\frac\right) \\ f'(0) &= 0 \end$
Further derivatives may be derived and evaluated as follows
$\begin f''(\alpha) &= \sum_ \frac \\ f''(0) &= \sum_ \frac \\ f^(\alpha) &= (-1)^n (n-2)!\sum_ \frac \\ f^(0) &= (-1)^n (n-2)!\sum_ \frac \end$
Hence solving for $D_\text(P \parallel Q)$ via the Taylor expansion of $f$ about $0$ evaluated at $\alpha=1$ yields
$\begin D_\text(P \parallel Q) &= \sum_^\infty \frac \\ &= \sum_^\infty \frac \sum_ \frac \end$
$P \leq 2Q$ a.s. is a sufficient condition for convergence of the series by the following absolute convergence argument
$\begin \sum_^\infty \left\vert\frac \sum_ \frac\right\vert &= \sum_^\infty \frac \sum_ \left\vert Q(x) - P(x) \right\vert \left\vert 1 - \frac \right\vert^ \\ &\leq \sum_^\infty \frac \sum_ \left\vert Q(x) - P(x) \right\vert \\ &\leq \sum_^\infty \frac \\ &= 1 \end$
$P \leq 2Q$ a.s. is also a necessary condition for convergence of the series by the following proof by contradiction. Assume that $P > 2Q$ with measure strictly greater than $0$. It then follows that there must exist some values $\varepsilon > 0$, $\rho > 0$, and $U < \infty$ such that $P \geq 2Q + \varepsilon$ and $Q \leq U$ with measure $\rho$. The previous proof of sufficiency demonstrated that the measure $1-\rho$ component of the series where $P \leq 2Q$ is bounded, so we need only concern ourselves with the behavior of the measure $\rho$ component of the series where $P \geq 2Q + \varepsilon$. The absolute value of the $n$th term of this component of the series is then lower bounded by $\frac1 \rho \left(1 + \frac\right)^n$, which is unbounded as $n \to \infty$, so the series diverges.

Duality formula for variational inference

The following result, due to Donsker and Varadhan, is known as Donsker and Varadhan's variational formula.

Examples

Multivariate normal distributions

Suppose that we have two multivariate normal distributions, with means $\mu_0, \mu_1$ and with (non-singular) covariance matrices $\Sigma_0, \Sigma_1.$ If the two distributions have the same dimension, , then the relative entropy between the distributions is as follows:

D_\text\left(\mathcal_0 \parallel \mathcal_1\right) =
\frac\left \operatorname\left(\Sigma_1^\Sigma_0\right) - k +
\left(\mu_1 - \mu_0\right)^\mathsf \Sigma_1^\left(\mu_1 - \mu_0\right) +
\ln \frac
\righttext

The logarithm in the last term must be taken to base since all terms apart from the last are base- logarithms of expressions that are either factors of the density function or otherwise arise naturally. The equation therefore gives a result measured in nats. Dividing the entire expression above by $\ln(2)$ yields the divergence in bits.

In a numerical implementation, it is helpful to express the result in terms of the Cholesky decompositions $L_0, L_1$ such that $\Sigma_0 = L_0 L_0^T$ and $\Sigma_1 = L_1 L_1^T$. Then with and solutions to the triangular linear systems $L_1 M = L_0$, and $L_1 y = \mu_1 - \mu_0$,

$D_\text\left(\mathcal_0 \parallel \mathcal_1\right) = \frac\left( \sum_^k ^2 - k + , y, ^2 + 2\sum_^k \ln \frac \right)\text$

A special case, and a common quantity in variational inference, is the relative entropy between a diagonal multivariate normal, and a standard normal distribution (with zero mean and unit variance):

D_\text\left(
\mathcal\left(\left(\mu_1, \ldots, \mu_k\right)^\mathsf, \operatorname \left(\sigma_1^2, \ldots, \sigma_k^2\right)\right) \parallel
\mathcal\left(\mathbf, \mathbf\right)
\right) =
\frac \sum_^k \left sigma_i^2 + \mu_i^2 - 1 - \ln\left(\sigma_i^2\right)\righttext

For two univariate normal distributions and the above simplifies to
$D_\text\left(\mathcal \parallel \mathcal\right) = \log \frac + \frac - \frac$

In the case of co-centered normal distributions with $k=\sigma_1/\sigma_0$, this simplifies to:

$D_\text\left(\mathcal \parallel \mathcal\right) = \log_2 k + (k^-1)/2/\ln(2) \mathrm$

Uniform distributions

Consider two uniform distributions, with the support of p= ,B/math> enclosed within q= ,D/math> (C\le A). Then the information gain is:

$D_\text\left(\mathcal \parallel \mathcal\right) = \log \frac$

Intuitively, the information gain to a times narrower uniform distribution contains $\log_2 k$ bits. This connects with the use of bits in computing, where $\log_2k$ bits would be needed to identify one element of a long stream.

Exponential family

The exponential family of distribution is given by

$p_X(x, \theta) = h(x) \exp\left(\theta^\mathsf T(x) - A(\theta)\right)$

where $h(x)$ is reference measure, $T(x)$ is sufficient statistics, $\theta$ is canonical natural parameters, and $A(\theta)$ is the log-partition function.

The KL divergence between two distributions $p(x, \theta_1)$ and $p(x, \theta_2)$ is given by

$D_(\theta_1 \parallel \theta_2) = ^\mathsf \mu_1 - A(\theta_1) + A(\theta_2)$

where \mu_1 = E_ (X)= \nabla A(\theta_1) is the mean parameter of $p(x, \theta_1)$.

For example, for the Poisson distribution with mean $\lambda$, the sufficient statistics $T(x) = x$, the natural parameter $\theta = \log \lambda$, and log partition function $A(\theta) = e^\theta$. As such, the divergence between two Poisson distributions with means $\lambda_1$ and $\lambda_2$ is

$D_(\lambda_1 \parallel \lambda_2) = \lambda_1 \log \frac - \lambda_1 + \lambda_2\text$

As another example, for a normal distribution with unit variance $N(\mu, 1)$, the sufficient statistics $T(x) = x$, the natural parameter $\theta = \mu$, and log partition function $A(\theta)=\mu^2/2$. Thus, the divergence between two normal distributions $N(\mu_1, 1)$ and $N(\mu_2, 1)$ is

$D_(\mu_1 \parallel \mu_2) = \left(\mu_1 - \mu_2\right) \mu_1 - \frac + \frac = \frac\text$

As final example, the divergence between a normal distribution with unit variance $N(\mu, 1)$ and a Poisson distribution with mean $\lambda$ is

$D_(\mu \parallel \lambda) = (\mu - \log \lambda) \mu - \frac + \lambda\text$

Relation to metrics

While relative entropy is a statistical distance, it is not a metric on the space of probability distributions, but instead it is a divergence. While metrics are symmetric and generalize ''linear'' distance, satisfying the triangle inequality, divergences are asymmetric in general and generalize ''squared'' distance, in some cases satisfying a generalized Pythagorean theorem. In general $D_\text(P \parallel Q)$ does not equal $D_\text(Q \parallel P)$, and while this can be symmetrized (see ), the asymmetry is an important part of the geometry.

It generates a topology on the space of probability distributions. More concretely, if $\$ is a sequence of distributions such that

$\lim_ D_\text(P_n\parallel Q) = 0\text$

then it is said that

$P_n \xrightarrow \, Q\text$

Pinsker's inequality entails that

$P_n \xrightarrow P \Rightarrow P_n \xrightarrow P\text$

where the latter stands for the usual convergence in total variation.

Fisher information metric

Relative entropy is directly related to the Fisher information metric. This can be made explicit as follows. Assume that the probability distributions and are both parameterized by some (possibly multi-dimensional) parameter $\theta$. Consider then two close by values of $P = P(\theta)$ and $Q = P(\theta_0)$ so that the parameter $\theta$ differs by only a small amount from the parameter value $\theta_0$. Specifically, up to first order one has (using the Einstein summation convention)
$P(\theta) = P(\theta_0) + \Delta\theta_j \, P_j(\theta_0) + \cdots$

with $\Delta\theta_j = (\theta - \theta_0)_j$ a small change of $\theta$ in the direction, and $P_j\left(\theta_0\right) = \frac(\theta_0)$ the corresponding rate of change in the probability distribution. Since relative entropy has an absolute minimum 0 for $P = Q$, i.e. $\theta = \theta_0$, it changes only to ''second'' order in the small parameters $\Delta\theta_j$. More formally, as for any minimum, the first derivatives of the divergence vanish

$\left.\frac\_ D_\text(P(\theta) \parallel P(\theta_0)) = 0,$

and by the Taylor expansion one has up to second order

$D_\text(P(\theta) \parallel P(\theta_0)) = \frac \, \Delta\theta_j \, \Delta\theta_k \, g_(\theta_0) + \cdots$

where the Hessian matrix of the divergence

$g_(\theta_0) = \left.\frac \_ D_\text(P(\theta) \parallel P(\theta_0))$

must be positive semidefinite. Letting $\theta_0$ vary (and dropping the subindex 0) the Hessian $g_(\theta)$ defines a (possibly degenerate) Riemannian metric on the parameter space, called the Fisher information metric.

Fisher information metric theorem

When $p_$ satisfies the following regularity conditions:

$\frac, \frac, \frac$ exist,
$\begin \left, \frac\ &< F(x): \int_^\infty F(x)\,dx < \infty, \\ \left, \frac\ &< G(x): \int_^\infty G(x)\,dx < \infty \\ \left, \frac\ &< H(x): \int_^\infty p(x, 0)H(x)\,dx < \xi < \infty \end$

where is independent of
$\left.\int_^\infty \frac\_\, dx = \left.\int_^\infty \frac\_\, dx = 0$

then:
$\mathcal(p(x, 0) \parallel p(x, \rho)) = \frac + \mathcal\left(\rho^3\right) \text \rho \to 0\text$

Variation of information

Another information-theoretic metric is variation of information, which is roughly a symmetrization of conditional entropy. It is a metric on the set of partitions of a discrete probability space.

MAUVE Metric

MAUVE is a measure of the statistical gap between two text distributions, such as the difference between text generated by a model and human-written text. This measure is computed using Kullback–Leibler divergences between the two distributions in a quantized embedding space of a foundation model.

Relation to other quantities of information theory

Many of the other quantities of information theory can be interpreted as applications of relative entropy to specific cases.

Self-information

The self-information, also known as the information content of a signal, random variable, or event is defined as the negative logarithm of the probability of the given outcome occurring.

When applied to a discrete random variable, the self-information can be represented as

$\operatorname \operatorname(m) = D_\text\left(\delta_\text \parallel \\right),$

is the relative entropy of the probability distribution $P(i)$ from a Kronecker delta representing certainty that $i = m$ — i.e. the number of extra bits that must be transmitted to identify if only the probability distribution $P(i)$ is available to the receiver, not the fact that $i = m$.

Mutual information

The mutual information,

\begin
\operatorname(X; Y)
&= D_\text(P_ \parallel P_X \cdot P_Y) \\
&= \operatorname_X _\text^Y(P_ \parallel P_Y)\\
&= \operatorname_Y _\text^X(P_ \parallel P_X)\end

is the relative entropy of the joint probability distribution $P_(x, y)$ from the product $(P_X \cdot P_Y)(x, y) = P_X(x) P_Y(y)$ of the two marginal probability distributions — i.e. the expected number of extra bits that must be transmitted to identify and if they are coded using only their marginal distributions instead of the joint distribution.

Shannon entropy

The Shannon entropy,

\begin
\Eta(X) &= \operatorname \left operatorname_X(x)\right\\
&= \log N - D_\text
\end

is the number of bits which would have to be transmitted to identify from equally likely possibilities, ''less'' the relative entropy of the uniform distribution on the random variates of , $P_U(X)$, from the true distribution $P(X)$ — i.e. ''less'' the expected number of bits saved, which would have had to be sent if the value of were coded according to the uniform distribution $P_U(X)$ rather than the true distribution $P(X)$. This definition of Shannon entropy forms the basis of E.T. Jaynes's alternative generalization to continuous distributions, the limiting density of discrete points (as opposed to the usual differential entropy), which defines the continuous entropy as
$\lim_ H_(X) = \log N - \int p(x)\log\frac\,dx\text$
which is equivalent to:
$\log(N) - D_\text(p(x), , m(x))$

Conditional entropy

The conditional entropy,

\begin
\Eta(X \mid Y)
&= \log N - D_\text(P(X, Y) \parallel P_U(X) P(Y)) \\ pt &= \log N - D_\text(P(X, Y) \parallel P(X) P(Y)) - D_\text(P(X) \parallel P_U(X)) \\ pt &= \Eta(X) - \operatorname(X; Y) \\ pt &= \log N - \operatorname_Y \left _\text\left(P\left(X \mid Y\right) \parallel P_U(X)\right)\right\end

is the number of bits which would have to be transmitted to identify from equally likely possibilities, ''less'' the relative entropy of the true joint distribution $P(X,Y)$ from the product distribution $P_U(X) P(Y)$ from — i.e. ''less'' the expected number of bits saved which would have had to be sent if the value of were coded according to the uniform distribution $P_U(X)$ rather than the conditional distribution $P(X, Y)$ of given .

Cross entropy

When we have a set of possible events, coming from the distribution , we can encode them (with a lossless data compression) using entropy encoding. This compresses the data by replacing each fixed-length input symbol with a corresponding unique, variable-length, prefix-free code (e.g.: the events (A, B, C) with probabilities p = (1/2, 1/4, 1/4) can be encoded as the bits (0, 10, 11)). If we know the distribution in advance, we can devise an encoding that would be optimal (e.g.: using Huffman coding). Meaning the messages we encode will have the shortest length on average (assuming the encoded events are sampled from ), which will be equal to Shannon's Entropy of (denoted as $\Eta(p)$). However, if we use a different probability distribution () when creating the entropy encoding scheme, then a larger number of bits will be used (on average) to identify an event from a set of possibilities. This new (larger) number is measured by the cross entropy between and .

The cross entropy between two probability distributions ( and ) measures the average number of bits needed to identify an event from a set of possibilities, if a coding scheme is used based on a given probability distribution , rather than the "true" distribution . The cross entropy for two distributions and over the same probability space is thus defined as follows.

\Eta(p, q) = \operatorname_p \log q= \Eta(p) + D_\text(p \parallel q)

For explicit derivation of this, see the Motivation section above.

Under this scenario, relative entropies (kl-divergence) can be interpreted as the extra number of bits, on average, that are needed (beyond $\Eta(p)$) for encoding the events because of using for constructing the encoding scheme instead of .

Bayesian updating

In Bayesian statistics, relative entropy can be used as a measure of the information gain in moving from a prior distribution to a posterior distribution: $p(x) \to p(x\mid I)$. If some new fact $Y = y$ is discovered, it can be used to update the posterior distribution for from $p(x\mid I)$ to a new posterior distribution $p(x\mid y,I)$ using Bayes' theorem:

$p(x \mid y, I) = \frac$

This distribution has a new entropy:

$\Eta\big(p(x \mid y, I)\big) = -\sum_x p(x \mid y, I) \log p(x \mid y, I)\text$

which may be less than or greater than the original entropy $\Eta(p(x\mid I))$. However, from the standpoint of the new probability distribution one can estimate that to have used the original code based on $p(x\mid I)$ instead of a new code based on $p(x\mid y, I)$ would have added an expected number of bits:

$D_\text\big(p(x \mid y, I) \parallel p(x \mid I) \big) = \sum_x p(x \mid y, I) \log \frac$

to the message length. This therefore represents the amount of useful information, or information gain, about , that has been learned by discovering $Y = y$.

If a further piece of data, $Y_2 = y_2$, subsequently comes in, the probability distribution for can be updated further, to give a new best guess $p(x \mid y_1, y_2, I)$. If one reinvestigates the information gain for using $p(x \mid y_1,I)$ rather than $p(x \mid I)$, it turns out that it may be either greater or less than previously estimated:

$\sum_x p(x \mid y_1, y_2, I) \log \frac$ may be ≤ or > than $\sum_x p(x \mid y_1, I) \log \frac$

and so the combined information gain does ''not'' obey the triangle inequality:

$D_\text \big( p(x \mid y_1, y_2, I) \parallel p(x \mid I) \big)$ may be <, = or > than $D_\text\big( p(x \mid y_1, y_2, I) \parallel p(x \mid y_1, I)\big) + D_\text\big(p(x \mid y_1, I) \parallel p(x \mid I)\big)$

All one can say is that on ''average'', averaging using $p(y_2 \mid y_1, x, I)$, the two sides will average out.

Bayesian experimental design

A common goal in Bayesian experimental design is to maximise the expected relative entropy between the prior and the posterior. When posteriors are approximated to be Gaussian distributions, a design maximising the expected relative entropy is called Bayes d-optimal.

Discrimination information

Relative entropy $D_\text\bigl(p(x \mid H_1) \parallel p(x \mid H_0)\bigr)$ can also be interpreted as the expected discrimination information for $H_1$ over $H_0$: the mean information per sample for discriminating in favor of a hypothesis $H_1$ against a hypothesis $H_0$, when hypothesis $H_1$ is true. Another name for this quantity, given to it by I. J. Good, is the expected weight of evidence for $H_1$ over $H_0$ to be expected from each sample.

The expected weight of evidence for $H_1$ over $H_0$ is not the same as the information gain expected per sample about the probability distribution $p(H)$ of the hypotheses,

$D_\text(p(x \mid H_1) \parallel p(x \mid H_0)) \neq IG = D_\text(p(H \mid x) \parallel p(H \mid I))\text$

Either of the two quantities can be used as a utility function in Bayesian experimental design, to choose an optimal next question to investigate: but they will in general lead to rather different experimental strategies.

On the entropy scale of ''information gain'' there is very little difference between near certainty and absolute certainty—coding according to a near certainty requires hardly any more bits than coding according to an absolute certainty. On the other hand, on the logit scale implied by weight of evidence, the difference between the two is enormous – infinite perhaps; this might reflect the difference between being almost sure (on a probabilistic level) that, say, the Riemann hypothesis is correct, compared to being certain that it is correct because one has a mathematical proof. These two different scales of loss function for uncertainty are ''both'' useful, according to how well each reflects the particular circumstances of the problem in question.

Principle of minimum discrimination information

The idea of relative entropy as discrimination information led Kullback to propose the Principle of (MDI): given new facts, a new distribution should be chosen which is as hard to discriminate from the original distribution $f_0$ as possible; so that the new data produces as small an information gain $D_\text(f \parallel f_0)$ as possible.

For example, if one had a prior distribution $p(x,a)$ over and , and subsequently learnt the true distribution of was $u(a)$, then the relative entropy between the new joint distribution for and , $q(x\mid a)u(a)$, and the earlier prior distribution would be:

$D_\text(q(x \mid a)u(a) \parallel p(x, a)) = \operatorname_\left\ + D_\text(u(a) \parallel p(a)),$

i.e. the sum of the relative entropy of $p(a)$ the prior distribution for from the updated distribution $u(a)$, plus the expected value (using the probability distribution $u(a)$) of the relative entropy of the prior conditional distribution $p(x\mid a)$ from the new conditional distribution $q(x\mid a)$. (Note that often the later expected value is called the ''conditional relative entropy'' (or ''conditional Kullback–Leibler divergence'') and denoted by $D_\text(q(x\mid a) \parallel p(x\mid a))$) This is minimized if $q(x\mid a)=p(x\mid a)$ over the whole support of $u(a)$; and we note that this result incorporates Bayes' theorem, if the new distribution $u(a)$ is in fact a δ function representing certainty that has one particular value.

MDI can be seen as an extension of Laplace's Principle of Insufficient Reason, and the Principle of Maximum Entropy of E.T. Jaynes. In particular, it is the natural extension of the principle of maximum entropy from discrete to continuous distributions, for which Shannon entropy ceases to be so useful (see '' differential entropy''), but the relative entropy continues to be just as relevant.

In the engineering literature, MDI is sometimes called the Principle of Minimum Cross-Entropy (MCE) or Minxent for short. Minimising relative entropy from to with respect to is equivalent to minimizing the cross-entropy of and , since

$\Eta(p, m) = \Eta(p) + D_\text(p \parallel m),$

which is appropriate if one is trying to choose an adequate approximation to . However, this is just as often ''not'' the task one is trying to achieve. Instead, just as often it is that is some fixed prior reference measure, and that one is attempting to optimise by minimising $D_\text(p \parallel m)$ subject to some constraint. This has led to some ambiguity in the literature, with some authors attempting to resolve the inconsistency by redefining cross-entropy to be $D_\text(p \parallel m)$, rather than $\Eta(p,m)$ .

Relationship to available work

Surprisals add where probabilities multiply. The surprisal for an event of probability is defined as $s = - k \ln p$. If is $\left\$ then surprisal is in $\$ so that, for instance, there are bits of surprisal for landing all "heads" on a toss of coins.

Best-guess states (e.g. for atoms in a gas) are inferred by maximizing the ''average surprisal'' (entropy) for a given set of control parameters (like pressure or volume ). This constrained entropy maximization, both classically and quantum mechanically, minimizes Gibbs availability in entropy units $A \equiv -k \ln Z$ where is a constrained multiplicity or partition function.

When temperature is fixed, free energy ($T \times A$) is also minimized. Thus if $T, V$ and number of molecules are constant, the Helmholtz free energy $F \equiv U - TS$ (where is energy and is entropy) is minimized as a system "equilibrates." If and are held constant (say during processes in your body), the Gibbs free energy $G = U + PV - TS$ is minimized instead. The change in free energy under these conditions is a measure of available work that might be done in the process. Thus available work for an ideal gas at constant temperature $T_o$ and pressure $P_o$ is $W = \Delta G = NkT_o\Theta(V/V_o)$ where $V_o = NkT_o/P_o$ and $\Theta(x) = x - 1 - \ln x \ge 0$ (see also Gibbs inequality).

More generally the work available relative to some ambient is obtained by multiplying ambient temperature $T_o$ by relative entropy or ''net surprisal'' $\Delta I \ge 0,$ defined as the average value of $k\ln(p/p_o)$ where $p_o$ is the probability of a given state under ambient conditions. For instance, the work available in equilibrating a monatomic ideal gas to ambient values of $V_o$ and $T_o$ is thus $W = T_o \Delta I$, where relative entropy

\Delta I = N k \left Theta + \frac \Theta\right

The resulting contours of constant relative entropy, shown at right for a mole of Argon at standard temperature and pressure, for example put limits on the conversion of hot to cold as in flame-powered air-conditioning or in the unpowered device to convert boiling-water to ice-water discussed here. Thus relative entropy measures thermodynamic availability in bits.

Quantum information theory

For density matrices and on a Hilbert space, the quantum relative entropy from to is defined to be

$D_\text(P \parallel Q) = \operatorname(P(\log P - \log Q)).$

In quantum information science the minimum of $D_\text(P\parallel Q)$ over all separable states can also be used as a measure of entanglement in the state .

Relationship between models and reality

Just as relative entropy of "actual from ambient" measures thermodynamic availability, relative entropy of "reality from a model" is also useful even if the only clues we have about reality are some experimental measurements. In the former case relative entropy describes ''distance to equilibrium'' or (when multiplied by ambient temperature) the amount of ''available work'', while in the latter case it tells you about surprises that reality has up its sleeve or, in other words, ''how much the model has yet to learn''.

Although this tool for evaluating models against systems that are accessible experimentally may be applied in any field, its application to selecting a statistical model via Akaike information criterion are particularly well described in papers and a book by Burnham and Anderson. In a nutshell the relative entropy of reality from a model may be estimated, to within a constant additive term, by a function of the deviations observed between data and the model's predictions (like the mean squared deviation) . Estimates of such divergence for models that share the same additive term can in turn be used to select among models.

When trying to fit parametrized models to data there are various estimators which attempt to minimize relative entropy, such as maximum likelihood and maximum spacing estimators.

Symmetrised divergence

also considered the symmetrized function:

$D_\text(P \parallel Q) + D_\text(Q \parallel P)$

which they referred to as the "divergence", though today the "KL divergence" refers to the asymmetric function (see for the evolution of the term). This function is symmetric and nonnegative, and had already been defined and used by Harold Jeffreys in 1948; it is accordingly called the Jeffreys divergence.

This quantity has sometimes been used for feature selection in classification problems, where and are the conditional pdfs of a feature under two different classes. In the Banking and Finance industries, this quantity is referred to as Population Stability Index (PSI), and is used to assess distributional shifts in model features through time.

An alternative is given via the $\lambda$-divergence,

$D_\lambda(P \parallel Q) = \lambda D_\text(P \parallel \lambda P + (1 - \lambda)Q) + (1 - \lambda) D_\text(Q \parallel \lambda P + (1 - \lambda)Q)\text$

which can be interpreted as the expected information gain about from discovering which probability distribution is drawn from, or , if they currently have probabilities $\lambda$ and $1-\lambda$ respectively.

The value $\lambda = 0.5$ gives the Jensen–Shannon divergence, defined by

$D_\text = \tfrac D_\text (P \parallel M) + \tfrac D_\text(Q \parallel M)$

where is the average of the two distributions,

$M = \tfrac \left(P + Q\right)\text$

We can also interpret $D_\text$ as the capacity of a noisy information channel with two inputs giving the output distributions and . The Jensen–Shannon divergence, like all -divergences, is ''locally'' proportional to the Fisher information metric. It is similar to the Hellinger metric (in the sense that it induces the same affine connection on a statistical manifold).

Furthermore, the Jensen–Shannon divergence can be generalized using abstract statistical M-mixtures relying on an abstract mean M.

Relationship to other probability-distance measures

There are many other important measures of probability distance. Some of these are particularly connected with relative entropy. For example:
* The total-variation distance, $\delta(p,q)$. This is connected to the divergence through Pinsker's inequality: $\delta(P, Q) \le \sqrt.$ Pinsker's inequality is vacuous for any distributions where $D_(P\parallel Q)>2$, since the total variation distance is at most . For such distributions, an alternative bound can be used, due to Bretagnolle and Huber (see, also, Tsybakov Equation 2.25.): $\delta(P,Q) \le \sqrt.$
* The family of Rényi divergences generalize relative entropy. Depending on the value of a certain parameter, $\alpha$, various inequalities may be deduced.

Other notable measures of distance include the Hellinger distance, ''histogram intersection'', '' Chi-squared statistic'', ''quadratic form distance'', '' match distance'', '' Kolmogorov–Smirnov distance'', and '' earth mover's distance''.

Data differencing

Just as ''absolute'' entropy serves as theoretical background for data ''compression'', ''relative'' entropy serves as theoretical background for data ''differencing'' – the absolute entropy of a set of data in this sense being the data required to reconstruct it (minimum compressed size), while the relative entropy of a target set of data, given a source set of data, is the data required to reconstruct the target ''given'' the source (minimum size of a patch).

See also

* Akaike information criterion
* Bayesian information criterion
* Bregman divergence
* Cross-entropy
* Deviance information criterion
* Entropic value at risk
* Entropy power inequality
*Hellinger distance
* Information gain in decision trees
* Information gain ratio
*Information theory and measure theory
* Jensen–Shannon divergence
* Quantum relative entropy
* Solomon Kullback and Richard Leibler
* Bhattacharyya distance

References

*
* . Republished by Dover Publications in 1968; reprinted in 1978: .
*

External links

Information Theoretical Estimators Toolbox

Ruby gem for calculating Kullback–Leibler divergence

Jon Shlens' tutorial on Kullback–Leibler divergence and likelihood theory

Matlab code for calculating Kullback–Leibler divergence for discrete distributions
* Sergio Verdú
Relative Entropy
NIPS 2009. One-hour video lecture.

A modern summary of info-theoretic divergence measures

{{DEFAULTSORT:Kullback-Leibler Divergence
Entropy and information
F-divergences
Information geometry
Thermodynamics