|
Einstein Summation Convention
In mathematics, especially the usage of linear algebra in Mathematical physics, Einstein notation (also known as the Einstein summation convention or Einstein summation notation) is a notational convention that implies summation over a set of indexed terms in a formula, thus achieving brevity. As part of mathematics it is a notational subset of Ricci calculus; however, it is often used in physics applications that do not distinguish between tangent and cotangent spaces. It was introduced to physics by Albert Einstein in 1916. Introduction Statement of convention According to this convention, when an index variable appears twice in a single term and is not otherwise defined (see Free and bound variables), it implies summation of that term over all the values of the index. So where the indices can range over the set , : y = \sum_^3 c_i x^i = c_1 x^1 + c_2 x^2 + c_3 x^3 is simplified by the convention to: : y = c_i x^i The upper indices are not exponents but are indices of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indexed Family
In mathematics, a family, or indexed family, is informally a collection of objects, each associated with an index from some index set. For example, a ''family of real numbers, indexed by the set of integers'' is a collection of real numbers, where a given function selects one real number for each integer (possibly the same). More formally, an indexed family is a mathematical function together with its domain I and image X. (that is, indexed families and mathematical functions are technically identical, just point of views are different.) Often the elements of the set X are referred to as making up the family. In this view, indexed families are interpreted as collections of indexed elements instead of functions. The set I is called the ''index set'' of the family, and X is the ''indexed set''. Sequences are one type of families indexed by natural numbers. In general, the index set I is not restricted to be countable. For example, one could consider an uncountable family of sub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Basis
In linear algebra, given a vector space ''V'' with a basis ''B'' of vectors indexed by an index set ''I'' (the cardinality of ''I'' is the dimension of ''V''), the dual set of ''B'' is a set ''B''∗ of vectors in the dual space ''V''∗ with the same index set ''I'' such that ''B'' and ''B''∗ form a biorthogonal system. The dual set is always linearly independent but does not necessarily span ''V''∗. If it does span ''V''∗, then ''B''∗ is called the dual basis or reciprocal basis for the basis ''B''. Denoting the indexed vector sets as B = \_ and B^ = \_, being biorthogonal means that the elements pair to have an inner product equal to 1 if the indexes are equal, and equal to 0 otherwise. Symbolically, evaluating a dual vector in ''V''∗ on a vector in the original space ''V'': : v^i\cdot v_j = \delta^i_j = \begin 1 & \text i = j\\ 0 & \text i \ne j\text \end where \delta^i_j is the Kronecker delta symbol. Introduction To perform operations with a vector, we must ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Description
Abstract may refer to: * ''Abstract'' (album), 1962 album by Joe Harriott * Abstract of title a summary of the documents affecting title to parcel of land * Abstract (law), a summary of a legal document * Abstract (summary), in academic publishing * Abstract art, artistic works that do not attempt to represent reality or concrete subjects * '' Abstract: The Art of Design'', 2017 Netflix documentary series * Abstract music, music that is non-representational * Abstract object in philosophy * Abstract structure in mathematics * Abstract type In programming languages, an abstract type is a type in a nominative type system that cannot be instantiated directly; a type that is not abstract – which ''can'' be instantiated – is called a ''concrete type''. Every instance of an abstrac ... in computer science * The property of an abstraction * Q-Tip (musician), also known as "The Abstract" * Abstract and concrete See also * Abstraction (other) {{Disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Change Of Basis
In mathematics, an ordered basis of a vector space of finite dimension allows representing uniquely any element of the vector space by a coordinate vector, which is a sequence of scalars called coordinates. If two different bases are considered, the coordinate vector that represents a vector on one basis is, in general, different from the coordinate vector that represents on the other basis. A change of basis consists of converting every assertion expressed in terms of coordinates relative to one basis into an assertion expressed in terms of coordinates relative to the other basis. Such a conversion results from the ''change-of-basis formula'' which expresses the coordinates relative to one basis in terms of coordinates relative to the other basis. Using matrices, this formula can be written :\mathbf x_\mathrm = A \,\mathbf x_\mathrm, where "old" and "new" refer respectively to the firstly defined basis and the other basis, \mathbf x_\mathrm and \mathbf x_\mathrm are the colu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covector
In mathematics, a linear form (also known as a linear functional, a one-form, or a covector) is a linear map from a vector space to its field of scalars (often, the real numbers or the complex numbers). If is a vector space over a field , the set of all linear functionals from to is itself a vector space over with addition and scalar multiplication defined pointwise. This space is called the dual space of , or sometimes the algebraic dual space, when a topological dual space is also considered. It is often denoted , p. 19, §3.1 or, when the field is understood, V^*; other notations are also used, such as V', V^ or V^. When vectors are represented by column vectors (as is common when a basis is fixed), then linear functionals are represented as row vectors, and their values on specific vectors are given by matrix products (with the row vector on the left). Examples * The constant zero function, mapping every vector to zero, is trivially a linear functional. * Indexing int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
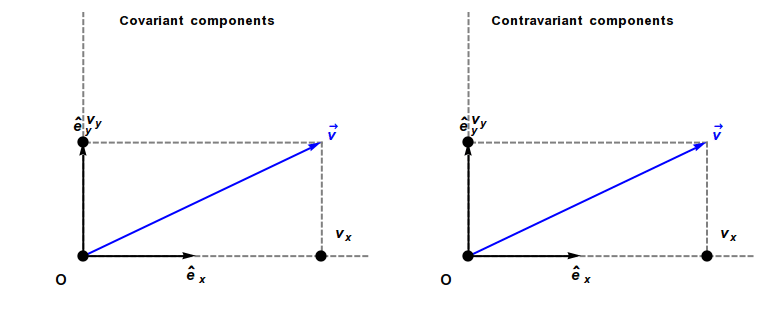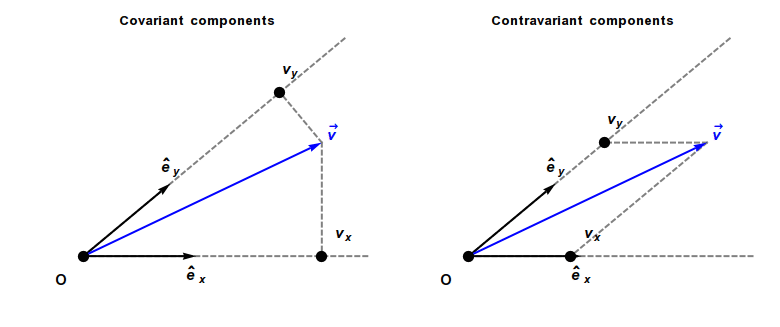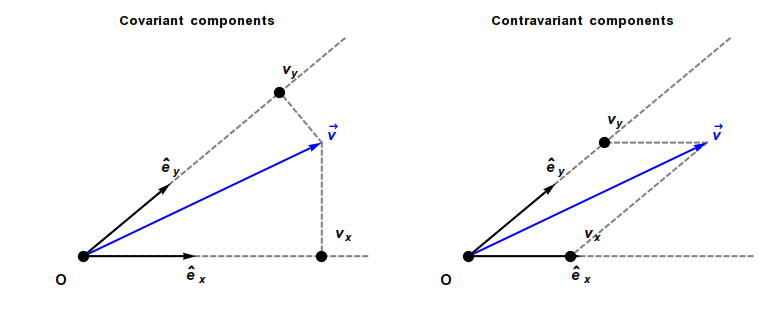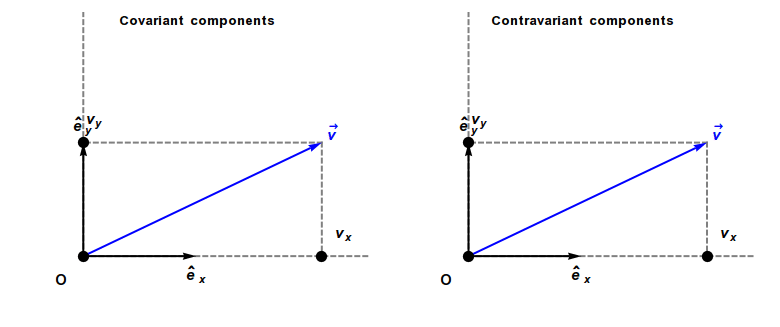
Covariant Vector
In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. In modern mathematical notation, the role is sometimes swapped. In physics, a basis is sometimes thought of as a set of reference axes. A change of scale on the reference axes corresponds to a change of units in the problem. For instance, by changing scale from meters to centimeters (that is, ''dividing'' the scale of the reference axes by 100), the components of a measured velocity vector are ''multiplied'' by 100. A vector changes scale ''inversely'' to changes in scale to the reference axes, and consequently is called ''contravariant''. As a result, a vector often has units of distance or distance with other units (as, for example, velocity has units of distance divided by time). In contrast, a covector, also called a ''dual vector'', typically has units of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Vector
In linear algebra, a coordinate vector is a representation of a vector as an ordered list of numbers (a tuple) that describes the vector in terms of a particular ordered basis. An easy example may be a position such as (5, 2, 1) in a 3-dimensional Cartesian coordinate system with the basis as the axes of this system. Coordinates are always specified relative to an ordered basis. Bases and their associated coordinate representations let one realize vector spaces and linear transformations concretely as column vectors, row vectors, and matrices; hence, they are useful in calculations. The idea of a coordinate vector can also be used for infinite-dimensional vector spaces, as addressed below. Definition Let ''V'' be a vector space of dimension ''n'' over a field ''F'' and let : B = \ be an ordered basis for ''V''. Then for every v \in V there is a unique linear combination of the basis vectors that equals '' v '': : v = \alpha _1 b_1 + \alpha _2 b_2 + \cdots + \alpha _n b_n . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance And Contravariance Of Vectors
In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. In modern mathematical notation, the role is sometimes swapped. In physics, a basis is sometimes thought of as a set of reference axes. A change of scale on the reference axes corresponds to a change of units in the problem. For instance, by changing scale from meters to centimeters (that is, ''dividing'' the scale of the reference axes by 100), the components of a measured velocity vector are ''multiplied'' by 100. A vector changes scale ''inversely'' to changes in scale to the reference axes, and consequently is called ''contravariant''. As a result, a vector often has units of distance or distance with other units (as, for example, velocity has units of distance divided by time). In contrast, a covector, also called a ''dual vector'', typically has units of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance And Contravariance Of Vectors
In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. In modern mathematical notation, the role is sometimes swapped. In physics, a basis is sometimes thought of as a set of reference axes. A change of scale on the reference axes corresponds to a change of units in the problem. For instance, by changing scale from meters to centimeters (that is, ''dividing'' the scale of the reference axes by 100), the components of a measured velocity vector are ''multiplied'' by 100. A vector changes scale ''inversely'' to changes in scale to the reference axes, and consequently is called ''contravariant''. As a result, a vector often has units of distance or distance with other units (as, for example, velocity has units of distance divided by time). In contrast, a covector, also called a ''dual vector'', typically has units of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Variable
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation (symbol) that specifies places in an expression where substitution may take place and is not a parameter of this or any container expression. Some older books use the terms real variable and apparent variable for free variable and bound variable, respectively. The idea is related to a placeholder (a symbol that will later be replaced by some value), or a wildcard character that stands for an unspecified symbol. In computer programming, the term free variable refers to variables used in a function that are neither local variables nor parameters of that function. The term non-local variable is often a synonym in this context. A bound variable, in contrast, is a variable that has been ''bound'' to a specific value or range of values in the domain of discourse or universe. This may be achieved through the use of logical quantifiers, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bound Variable
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a Mathematical notation, notation (symbol) that specifies places in an expression (mathematics), expression where Substitution (logic), substitution may take place and is not a parameter of this or any container expression. Some older books use the terms real variable and apparent variable for free variable and bound variable, respectively. The idea is related to a placeholder (a symbol that will later be replaced by some value), or a wildcard character that stands for an unspecified symbol. In computer programming, the term free variable refers to variable (programming), variables used in a function (computer science), function that are neither local variables nor parameter (computer programming), parameters of that function. The term non-local variable is often a synonym in this context. A bound variable, in contrast, is a variable that ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
