Mathematics on:
[Wikipedia]
[Google]
[Amazon]
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their
an
"math, ''n.3''"
. ''Oxford English Dictionary,'' on-line version (2012).
 Number theory began with the manipulation of numbers, that is, natural numbers and later expanded to integers and rational numbers Number theory was once called arithmetic, but nowadays this term is mostly used for numerical calculations. Number theory dates back to ancient
Number theory began with the manipulation of numbers, that is, natural numbers and later expanded to integers and rational numbers Number theory was once called arithmetic, but nowadays this term is mostly used for numerical calculations. Number theory dates back to ancient
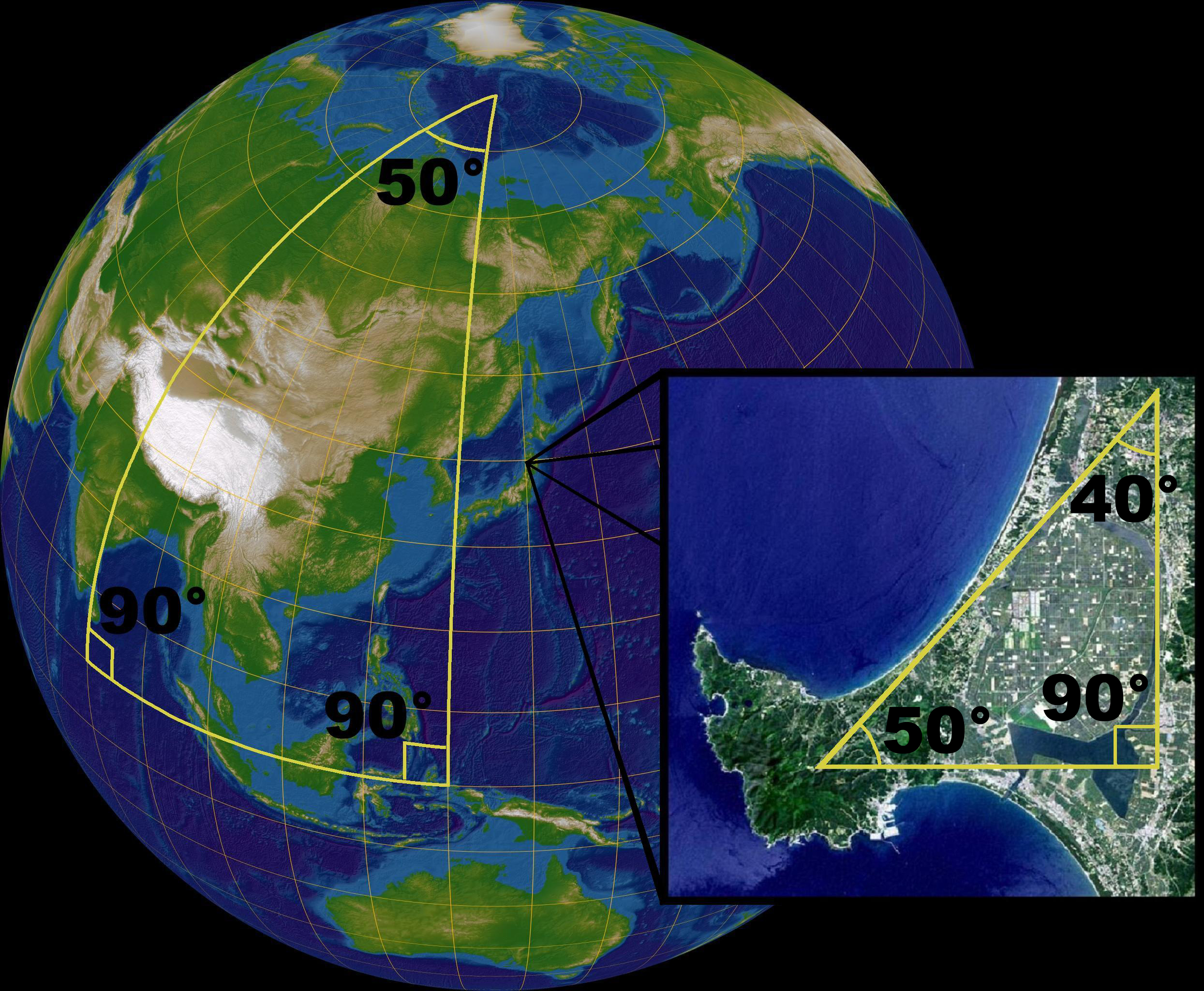 Geometry is one of the oldest branches of mathematics. It started with empirical recipes concerning shapes, such as lines,
Geometry is one of the oldest branches of mathematics. It started with empirical recipes concerning shapes, such as lines,

 Algebra is the art of manipulating
Algebra is the art of manipulating
 Calculus, formerly called infinitesimal calculus, was introduced independently and simultaneously by 17th-century mathematicians
Calculus, formerly called infinitesimal calculus, was introduced independently and simultaneously by 17th-century mathematicians
 Discrete mathematics, broadly speaking, is the study of individual, countable mathematical objects. An example is the set of all integers. Because the objects of study here are discrete, the methods of calculus and mathematical analysis do not directly apply. Algorithmsespecially their implementation and
Discrete mathematics, broadly speaking, is the study of individual, countable mathematical objects. An example is the set of all integers. Because the objects of study here are discrete, the methods of calculus and mathematical analysis do not directly apply. Algorithmsespecially their implementation and
 The two subjects of mathematical logic and set theory have belonged to mathematics since the end of the 19th century. Before this period, sets were not considered to be mathematical objects, and logic, although used for mathematical proofs, belonged to
The two subjects of mathematical logic and set theory have belonged to mathematics since the end of the 19th century. Before this period, sets were not considered to be mathematical objects, and logic, although used for mathematical proofs, belonged to
 The field of statistics is a mathematical application that is employed for the collection and processing of data samples, using procedures based on mathematical methods especially probability theory. Statisticians generate data with random sampling or randomized experiments. The design of a statistical sample or experiment determines the analytical methods that will be used. Analysis of data from observational studies is done using
The field of statistics is a mathematical application that is employed for the collection and processing of data samples, using procedures based on mathematical methods especially probability theory. Statisticians generate data with random sampling or randomized experiments. The design of a statistical sample or experiment determines the analytical methods that will be used. Analysis of data from observational studies is done using
 Evidence for more complex mathematics does not appear until around 3000 , when the
Evidence for more complex mathematics does not appear until around 3000 , when the
academic discipline
An academy (Attic Greek: Ἀκαδήμεια; Koine Greek Ἀκαδημία) is an institution of secondary education, secondary or tertiary education, tertiary higher education, higher learning (and generally also research or honorary membershi ...
.
Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a con ...
them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or f ...
s. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of the theory under consideration.
Mathematics is essential in the natural science
Natural science is one of the branches of science concerned with the description, understanding and prediction of natural phenomena, based on empirical evidence from observation and experimentation. Mechanisms such as peer review and repeatab ...
s, engineering, medicine, finance
Finance is the study and discipline of money, currency and capital assets. It is related to, but not synonymous with economics, the study of production, distribution, and consumption of money, assets, goods and services (the discipline of ...
, computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includin ...
and the social sciences. Although mathematics is extensively used for modeling phenomena, the fundamental truths of mathematics are independent from any scientific experimentation. Some areas of mathematics, such as statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of ...
and game theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has appli ...
, are developed in close correlation with their applications and are often grouped under applied mathematics
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathemat ...
. Other areas are developed independently from any application (and are therefore called pure mathematics
Pure mathematics is the study of mathematical concepts independently of any application outside mathematics. These concepts may originate in real-world concerns, and the results obtained may later turn out to be useful for practical applications, ...
), but often later find practical applications. The problem of integer factorization
In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these factors are further restricted to prime numbers, the process is called prime factorization.
When the numbers are suf ...
, for example, which goes back to Euclid in 300 BC, had no practical application before its use in the RSA cryptosystem
RSA (Rivest–Shamir–Adleman) is a public-key cryptosystem that is widely used for secure data transmission. It is also one of the oldest. The acronym "RSA" comes from the surnames of Ron Rivest, Adi Shamir and Leonard Adleman, who publicly ...
, now widely used for the security of computer networks.
Historically, the concept of a proof and its associated mathematical rigour
Rigour (British English) or rigor (American English; see spelling differences) describes a condition of stiffness or strictness. These constraints may be environmentally imposed, such as "the rigours of famine"; logically imposed, such as m ...
first appeared in Greek mathematics
Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly extant from the 7th century BC to the 4th century AD, around the shores of the Eastern Mediterranean. Greek mathem ...
, most notably in Euclid's ''Elements
Element or elements may refer to:
Science
* Chemical element, a pure substance of one type of atom
* Heating element, a device that generates heat by electrical resistance
* Orbital elements, parameters required to identify a specific orbit of ...
''. Since its beginning, mathematics was essentially divided into geometry and arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
(the manipulation of natural numbers and fractions), until the 16th and 17th centuries, when algebra and infinitesimal calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
were introduced as new areas. Since then, the interaction between mathematical innovations and scientific discoveries has led to a rapid lockstep increase in the development of both. At the end of the 19th century, the foundational crisis of mathematics led to the systematization of the axiomatic method, which heralded a dramatic increase in the number of mathematical areas and their fields of application. The contemporary Mathematics Subject Classification lists more than 60 first-level areas of mathematics.
Etymology
The word ''mathematics'' comes fromAncient Greek
Ancient Greek includes the forms of the Greek language used in ancient Greece and the ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Dark Ages (), the Archaic p ...
''máthēma'' ('), meaning 'that which is learnt', 'what one gets to know', hence also 'study' and 'science'. The word came to have the narrower and more technical meaning of 'mathematical study' even in Classical times. Its adjective
In linguistics, an adjective ( abbreviated ) is a word that generally modifies a noun or noun phrase or describes its referent. Its semantic role is to change information given by the noun.
Traditionally, adjectives were considered one of the ...
is ''mathēmatikós'' (), meaning 'related to learning' or 'studious', which likewise further came to mean 'mathematical'. In particular, ''mathēmatikḗ tékhnē'' (; la, ars mathematica) meant 'the mathematical art'.
Similarly, one of the two main schools of thought in Pythagoreanism was known as the ''mathēmatikoi'' (μαθηματικοί)which at the time meant 'learners' rather than 'mathematicians' in the modern sense. The Pythagoreans were likely the first to constrain the use of the word to just the study of arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
and geometry. By the time of Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical Greece, Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatet ...
(384–322 BC) this meaning was fully established.
In Latin, and in English until around 1700, the term ''mathematics'' more commonly meant 'astrology
Astrology is a range of divinatory practices, recognized as pseudoscientific since the 18th century, that claim to discern information about human affairs and terrestrial events by studying the apparent positions of celestial objects. Di ...
' (or sometimes 'astronomy
Astronomy () is a natural science that studies astronomical object, celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and chronology of the Universe, evolution. Objects of interest ...
') rather than 'mathematics'; the meaning gradually changed to its present one from about 1500 to 1800. This change has resulted in several mistranslations: For example, Saint Augustine's warning that Christians should beware of ''mathematici'', meaning 'astrologers', is sometimes mistranslated as a condemnation of mathematicians.
The apparent plural form in English goes back to the Latin neuter
Neuter is a Latin adjective meaning "neither", and can refer to:
* Neuter gender, a grammatical gender, a linguistic class of nouns triggering specific types of inflections in associated words
*Neuter pronoun
*Neutering, the sterilization of an ...
plural (Cicero
Marcus Tullius Cicero ( ; ; 3 January 106 BC – 7 December 43 BC) was a Roman statesman, lawyer, scholar, philosopher, and academic skeptic, who tried to uphold optimate principles during the political crises that led to the est ...
), based on the Greek plural ''ta mathēmatiká'' () and means roughly "all things mathematical", although it is plausible that English borrowed only the adjective ''mathematic(al)'' and formed the noun ''mathematics'' anew, after the pattern of '' physics'' and ''metaphysics
Metaphysics is the branch of philosophy that studies the fundamental nature of reality, the first principles of being, identity and change, space and time, causality, necessity, and possibility. It includes questions about the nature of conscio ...
'', inherited from Greek. In English, the noun ''mathematics'' takes a singular verb. It is often shortened to ''maths'' or, in North America, ''math''."maths, ''n.''"an
"math, ''n.3''"
. ''Oxford English Dictionary,'' on-line version (2012).
Areas of mathematics
Before the Renaissance, mathematics was divided into two main areas: arithmeticregarding the manipulation of numbers, and geometry, regarding the study of shapes. Some types of pseudoscience, such asnumerology
Numerology (also known as arithmancy) is the belief in an occult, divine or mystical relationship between a number and one or more coinciding events. It is also the study of the numerical value, via an alphanumeric system, of the letters in ...
and astrology, were not then clearly distinguished from mathematics.
During the Renaissance, two more areas appeared. Mathematical notation led to algebra which, roughly speaking, consists of the study and the manipulation of formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwee ...
s. Calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
, consisting of the two subfields ''differential calculus
In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve. ...
'' and '' integral calculus'', is the study of continuous functions, which model the typically nonlinear relationships between varying quantities, as represented by variables. This division into four main areasarithmetic, geometry, algebra, calculusendured until the end of the 19th century. Areas such as celestial mechanics and solid mechanics were then studied by mathematicians, but now are considered as belonging to physics. The subject of combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many appl ...
has been studied for much of recorded history, yet did not become a separate branch of mathematics until the seventeenth century.
At the end of the 19th century, the foundational crisis in mathematics and the resulting systematization of the axiomatic method led to an explosion of new areas of mathematics. The 2020 Mathematics Subject Classification contains no less than first-level areas. Some of these areas correspond to the older division, as is true regarding number theory (the modern name for higher arithmetic
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777� ...
) and geometry. Several other first-level areas have "geometry" in their names or are otherwise commonly considered part of geometry. Algebra and calculus do not appear as first-level areas but are respectively split into several first-level areas. Other first-level areas emerged during the 20th century or had not previously been considered as mathematics, such as mathematical logic and foundations.
Number theory
 Number theory began with the manipulation of numbers, that is, natural numbers and later expanded to integers and rational numbers Number theory was once called arithmetic, but nowadays this term is mostly used for numerical calculations. Number theory dates back to ancient
Number theory began with the manipulation of numbers, that is, natural numbers and later expanded to integers and rational numbers Number theory was once called arithmetic, but nowadays this term is mostly used for numerical calculations. Number theory dates back to ancient Babylon
''Bābili(m)''
* sux, 𒆍𒀭𒊏𒆠
* arc, 𐡁𐡁𐡋 ''Bāḇel''
* syc, ܒܒܠ ''Bāḇel''
* grc-gre, Βαβυλών ''Babylṓn''
* he, בָּבֶל ''Bāvel''
* peo, 𐎲𐎠𐎲𐎡𐎽𐎢 ''Bābiru''
* elx, 𒀸𒁀𒉿𒇷 ''Babi ...
and probably China
China, officially the People's Republic of China (PRC), is a country in East Asia. It is the world's List of countries and dependencies by population, most populous country, with a Population of China, population exceeding 1.4 billion, slig ...
. Two prominent early number theorists were Euclid of ancient Greece and Diophantus
Diophantus of Alexandria ( grc, Διόφαντος ὁ Ἀλεξανδρεύς; born probably sometime between AD 200 and 214; died around the age of 84, probably sometime between AD 284 and 298) was an Alexandrian mathematician, who was the aut ...
of Alexandria. The modern study of number theory in its abstract form is largely attributed to Pierre de Fermat and Leonhard Euler. The field came to full fruition with the contributions of Adrien-Marie Legendre and Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refe ...
.
Many easily stated number problems have solutions that require sophisticated methods, often from across mathematics. A prominent example is Fermat's Last Theorem
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers , , and satisfy the equation for any integer value of greater than 2. The cases and have bee ...
. This conjecture was stated in 1637 by Pierre de Fermat, but it was proved only in 1994 by Andrew Wiles, who used tools including scheme theory from algebraic geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrica ...
, category theory
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, ca ...
, and homological algebra
Homological algebra is the branch of mathematics that studies homology (mathematics), homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology (a precurs ...
. Another example is Goldbach's conjecture
Goldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even natural number greater than 2 is the sum of two prime numbers.
The conjecture has been shown to hold ...
, which asserts that every even integer greater than 2 is the sum of two prime numbers. Stated in 1742 by Christian Goldbach
Christian Goldbach (; ; 18 March 1690 – 20 November 1764) was a German mathematician connected with some important research mainly in number theory; he also studied law and took an interest in and a role in the Russian court. After traveling ...
, it remains unproven despite considerable effort.
Number theory includes several subareas, including analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of D ...
, algebraic number theory
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic ...
, geometry of numbers (method oriented), diophantine equation
In mathematics, a Diophantine equation is an equation, typically a polynomial equation in two or more unknowns with integer coefficients, such that the only solutions of interest are the integer ones. A linear Diophantine equation equates to a c ...
s, and transcendence theory
Transcendental number theory is a branch of number theory that investigates transcendental numbers (numbers that are not solutions of any polynomial equation with rational coefficients), in both qualitative and quantitative ways.
Transcendence ...
(problem oriented).
Geometry
 Geometry is one of the oldest branches of mathematics. It started with empirical recipes concerning shapes, such as lines,
Geometry is one of the oldest branches of mathematics. It started with empirical recipes concerning shapes, such as lines, angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ...
s and circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
s, which were developed mainly for the needs of surveying
Surveying or land surveying is the technique, profession, art, and science of determining the terrestrial two-dimensional or three-dimensional positions of points and the distances and angles between them. A land surveying professional is ca ...
and architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and constructing buildings ...
, but has since blossomed out into many other subfields.
A fundamental innovation was the ancient Greeks' introduction of the concept of proofs, which require that every assertion must be ''proved''. For example, it is not sufficient to verify by measurement
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events.
In other words, measurement is a process of determining how large or small a physical quantity is as compared ...
that, say, two lengths are equal; their equality must be proven via reasoning from previously accepted results ( theorems) and a few basic statements. The basic statements are not subject to proof because they are self-evident ( postulates), or are part of the definition of the subject of study (axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or f ...
s). This principle, foundational for all mathematics, was first elaborated for geometry, and was systematized by Euclid around 300 BC in his book ''Elements
Element or elements may refer to:
Science
* Chemical element, a pure substance of one type of atom
* Heating element, a device that generates heat by electrical resistance
* Orbital elements, parameters required to identify a specific orbit of ...
''.
The resulting Euclidean geometry is the study of shapes and their arrangements constructed from lines, planes
Plane(s) most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
Plane or planes may also refer to:
Biology
* Plane (tree) or ''Platanus'', wetland native plant
* ''Planes' ...
and circles in the Euclidean plane
In mathematics, the Euclidean plane is a Euclidean space of dimension two. That is, a geometric setting in which two real quantities are required to determine the position of each point ( element of the plane), which includes affine notions of ...
( plane geometry) and the three-dimensional Euclidean space.
Euclidean geometry was developed without change of methods or scope until the 17th century, when René Descartes introduced what is now called Cartesian coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...
. This constituted a major change of paradigm: Instead of defining real numbers as lengths of line segments (see number line), it allowed the representation of points using their ''coordinates'', which are numbers. Algebra (and later, calculus) can thus be used to solve geometrical problems. Geometry was split into two new subfields: synthetic geometry, which uses purely geometrical methods, and analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineerin ...
, which uses coordinates systemically.
Analytic geometry allows the study of curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line (geometry), line, but that does not have to be Linearity, straight.
Intuitively, a curve may be thought of as the trace left by a moving point (ge ...
s unrelated to circles and lines. Such curves can be defined as the graph of functions, the study of which led to differential geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multili ...
. They can also be defined as implicit equations, often polynomial equations (which spawned algebraic geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrica ...
). Analytic geometry also makes it possible to consider Euclidean spaces of higher than three dimensions.
In the 19th century, mathematicians discovered non-Euclidean geometries, which do not follow the parallel postulate. By questioning that postulate's truth, this discovery has been viewed as joining Russel's paradox
In mathematical logic, Russell's paradox (also known as Russell's antinomy) is a set-theoretic paradox discovered by the British philosopher and mathematician Bertrand Russell in 1901. Russell's paradox shows that every set theory that contains a ...
in revealing the foundational crisis of mathematics. This aspect of the crisis was solved by systematizing the axiomatic method, and adopting that the truth of the chosen axioms is not a mathematical problem. In turn, the axiomatic method allows for the study of various geometries obtained either by changing the axioms or by considering properties that do not change under specific transformations of the space.
Today's subareas of geometry include:
* Projective geometry, introduced in the 16th century by Girard Desargues, extends Euclidean geometry by adding points at infinity at which parallel lines intersect. This simplifies many aspects of classical geometry by unifying the treatments for intersecting and parallel lines.
* Affine geometry, the study of properties relative to parallelism and independent from the concept of length.
*Differential geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multili ...
, the study of curves, surfaces, and their generalizations, which are defined using differentiable functions.
* Manifold theory, the study of shapes that are not necessarily embedded in a larger space.
* Riemannian geometry, the study of distance properties in curved spaces.
*Algebraic geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrica ...
, the study of curves, surfaces, and their generalizations, which are defined using polynomials.
* Topology, the study of properties that are kept under continuous deformation
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deforma ...
s.
** Algebraic topology, the use in topology of algebraic methods, mainly homological algebra
Homological algebra is the branch of mathematics that studies homology (mathematics), homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology (a precurs ...
.
* Discrete geometry, the study of finite configurations in geometry.
* Convex geometry, the study of convex sets, which takes its importance from its applications in optimization.
* Complex geometry, the geometry obtained by replacing real numbers with complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s.
Algebra
equation
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, in ...
s and formulas. Diophantus (3rd century) and al-Khwarizmi (9th century) were the two main precursors of algebra. Diophantus solved some equations involving unknown natural numbers by deducing new relations until he obtained the solution. Al-Khwarizmi introduced systematic methods for transforming equations, such as moving a term from one side of an equation into the other side. The term ''algebra'' is derived from the Arabic
Arabic (, ' ; , ' or ) is a Semitic language spoken primarily across the Arab world.Semitic languages: an international handbook / edited by Stefan Weninger; in collaboration with Geoffrey Khan, Michael P. Streck, Janet C. E.Watson; Walte ...
word ''al-jabr'' meaning 'the reunion of broken parts' that he used for naming one of these methods in the title of his main treatise.
Algebra became an area in its own right only with François Viète (1540–1603), who introduced the use of variables for representing unknown or unspecified numbers. Variables allow mathematicians to describe the operations that have to be done on the numbers represented using mathematical formulas.
Until the 19th century, algebra consisted mainly of the study of linear equation
In mathematics, a linear equation is an equation that may be put in the form
a_1x_1+\ldots+a_nx_n+b=0, where x_1,\ldots,x_n are the variables (or unknowns), and b,a_1,\ldots,a_n are the coefficients, which are often real numbers. The coefficien ...
s (presently '' linear algebra''), and polynomial equations in a single unknown, which were called ''algebraic equations'' (a term still in use, although it may be ambiguous). During the 19th century, mathematicians began to use variables to represent things other than numbers (such as matrices, modular integers, and geometric transformations), on which generalizations of arithmetic operations are often valid. The concept of algebraic structure
In mathematics, an algebraic structure consists of a nonempty set ''A'' (called the underlying set, carrier set or domain), a collection of operations on ''A'' (typically binary operations such as addition and multiplication), and a finite set of ...
addresses this, consisting of a set whose elements are unspecified, of operations acting on the elements of the set, and rules that these operations must follow. The scope of algebra thus grew to include the study of algebraic structures. This object of algebra was called ''modern algebra'' or abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures. Algebraic structures include groups, rings, fields, modules, vector spaces, lattices, and algebras over a field. The te ...
, as established by the influence and works of Emmy Noether. (The latter term appears mainly in an educational context, in opposition to elementary algebra, which is concerned with the older way of manipulating formulas.)
Some types of algebraic structures have useful and often fundamental properties, in many areas of mathematics. Their study became autonomous parts of algebra, and include:
*group theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field ...
;
* field theory;
* vector spaces, whose study is essentially the same as linear algebra;
* ring theory;
* commutative algebra, which is the study of commutative ring
In mathematics, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra. Complementarily, noncommutative algebra is the study of ring properties that are not ...
s, includes the study of polynomials, and is a foundational part of algebraic geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrica ...
;
*homological algebra
Homological algebra is the branch of mathematics that studies homology (mathematics), homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology (a precurs ...
;
*Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an Binary operation, operation called the Lie bracket, an Alternating multilinear map, alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow ...
and Lie group
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additio ...
theory;
*Boolean algebra
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values ''true'' and ''false'', usually denoted 1 and 0, whereas ...
, which is widely used for the study of the logical structure of computer
A computer is a machine that can be programmed to Execution (computing), carry out sequences of arithmetic or logical operations (computation) automatically. Modern digital electronic computers can perform generic sets of operations known as C ...
s.
The study of types of algebraic structures as mathematical objects is the purpose of universal algebra and category theory
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, ca ...
. The latter applies to every mathematical structure
In mathematics, a structure is a set endowed with some additional features on the set (e.g. an operation, relation, metric, or topology). Often, the additional features are attached or related to the set, so as to provide it with some additional ...
(not only algebraic ones). At its origin, it was introduced, together with homological algebra for allowing the algebraic study of non-algebraic objects such as topological spaces; this particular area of application is called algebraic topology.
Calculus and analysis
Newton
Newton most commonly refers to:
* Isaac Newton (1642–1726/1727), English scientist
* Newton (unit), SI unit of force named after Isaac Newton
Newton may also refer to:
Arts and entertainment
* ''Newton'' (film), a 2017 Indian film
* Newton ( ...
and Leibniz. It is fundamentally the study of the relationship of variables that depend on each other. Calculus was expanded in the 18th century by Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in ma ...
with the introduction of the concept of a function and many other results. Presently, "calculus" refers mainly to the elementary part of this theory, and "analysis" is commonly used for advanced parts.
Analysis is further subdivided into real analysis, where variables represent real numbers, and complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates Function (mathematics), functions of complex numbers. It is helpful in many branches of mathemati ...
, where variables represent complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s. Analysis includes many subareas shared by other areas of mathematics which include:
* Multivariable calculus
* Functional analysis, where variables represent varying functions;
* Integration
Integration may refer to:
Biology
* Multisensory integration
* Path integration
* Pre-integration complex, viral genetic material used to insert a viral genome into a host genome
*DNA integration, by means of site-specific recombinase technolo ...
, measure theory
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures ( length, area, volume) and other common notions, such as mass and probability of events. These seemingly distinct concepts have many simil ...
and potential theory, all strongly related with probability theory on a continuum;
* Ordinary differential equations;
* Partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a Multivariable calculus, multivariable function.
The function is often thought of as an "unknown" to be sol ...
s;
* Numerical analysis, mainly devoted to the computation on computers of solutions of ordinary and partial differential equations that arise in many applications.
Discrete mathematics
computational complexity
In computer science, the computational complexity or simply complexity of an algorithm is the amount of resources required to run it. Particular focus is given to computation time (generally measured by the number of needed elementary operations) ...
play a major role in discrete mathematics.
The four color theorem
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions sh ...
and optimal sphere packing were two major problems of discrete mathematics solved in the second half of the 20th century. The P versus NP problem, which remains open to this day, is also important for discrete mathematics, since its solution would potentially impact a large number of computationally difficult problems.
Discrete mathematics includes:
* Combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many appl ...
, the art of enumerating mathematical objects that satisfy some given constraints. Originally, these objects were elements or subset
In mathematics, Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are ...
s of a given set; this has been extended to various objects, which establishes a strong link between combinatorics and other parts of discrete mathematics. For example, discrete geometry includes counting configurations of geometric shape
A shape or figure is a graphical representation of an object or its external boundary, outline, or external surface, as opposed to other properties such as color, texture, or material type.
A plane shape or plane figure is constrained to lie on ...
s
* Graph theory and hypergraphs
* Coding theory, including error correcting codes and a part of cryptography
Cryptography, or cryptology (from grc, , translit=kryptós "hidden, secret"; and ''graphein'', "to write", or ''-logia'', "study", respectively), is the practice and study of techniques for secure communication in the presence of adve ...
* Matroid theory
* Discrete geometry
* Discrete probability distributions
* Game theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has appli ...
(although continuous game
A continuous game is a mathematical concept, used in game theory, that generalizes the idea of an ordinary game like tic-tac-toe (noughts and crosses) or checkers (draughts). In other words, it extends the notion of a discrete game, where the playe ...
s are also studied, most common games, such as chess and poker
Poker is a family of comparing card games in which players wager over which hand is best according to that specific game's rules. It is played worldwide, however in some places the rules may vary. While the earliest known form of the game w ...
are discrete)
* Discrete optimization, including combinatorial optimization, integer programming, constraint programming
Mathematical logic and set theory
 The two subjects of mathematical logic and set theory have belonged to mathematics since the end of the 19th century. Before this period, sets were not considered to be mathematical objects, and logic, although used for mathematical proofs, belonged to
The two subjects of mathematical logic and set theory have belonged to mathematics since the end of the 19th century. Before this period, sets were not considered to be mathematical objects, and logic, although used for mathematical proofs, belonged to philosophy
Philosophy (from , ) is the systematized study of general and fundamental questions, such as those about existence, reason, knowledge, values, mind, and language. Such questions are often posed as problems to be studied or resolved. Some ...
and was not specifically studied by mathematicians.
Before Cantor's study of infinite sets, mathematicians were reluctant to consider actually infinite collections, and considered infinity
Infinity is that which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
Since the time of the ancient Greeks, the philosophical nature of infinity was the subject of many discussions amo ...
to be the result of endless enumeration. Cantor's work offended many mathematicians not only by considering actually infinite sets but by showing that this implies different sizes of infinity, per Cantor's diagonal argument. This led to the controversy over Cantor's set theory.
In the same period, various areas of mathematics concluded the former intuitive definitions of the basic mathematical objects were insufficient for ensuring mathematical rigour
Rigour (British English) or rigor (American English; see spelling differences) describes a condition of stiffness or strictness. These constraints may be environmentally imposed, such as "the rigours of famine"; logically imposed, such as m ...
. Examples of such intuitive definitions are "a set is a collection of objects", "natural number is what is used for counting", "a point is a shape with a zero length in every direction", "a curve is a trace left by a moving point", etc.
This became the foundational crisis of mathematics. It was eventually solved in mainstream mathematics by systematizing the axiomatic method inside a formalized set theory. Roughly speaking, each mathematical object is defined by the set of all similar objects and the properties that these objects must have. For example, in Peano arithmetic
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano. These axioms have been used nearly u ...
, the natural numbers are defined by "zero is a number", "each number has a unique successor", "each number but zero has a unique predecessor", and some rules of reasoning. This mathematical abstraction
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
from reality is embodied in the modern philosophy of formalism, as founded by David Hilbert
David Hilbert (; ; 23 January 1862 – 14 February 1943) was a German mathematician, one of the most influential mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many ...
around 1910.
The "nature" of the objects defined this way is a philosophical problem that mathematicians leave to philosophers, even if many mathematicians have opinions on this nature, and use their opinionsometimes called "intuition"to guide their study and proofs. The approach allows considering "logics" (that is, sets of allowed deducing rules), theorems, proofs, etc. as mathematical objects, and to prove theorems about them. For example, Gödel's incompleteness theorems
Gödel's incompleteness theorems are two theorems of mathematical logic
Mathematical logic is the study of logic, formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory. Research i ...
assert, roughly speaking that, in every consistent formal system that contains the natural numbers, there are theorems that are true (that is provable in a stronger system), but not provable inside the system. This approach to the foundations of mathematics was challenged during the first half of the 20th century by mathematicians led by Brouwer Brouwer (also Brouwers and de Brouwer) is a Dutch and Flemish surname. The word ''brouwer'' means 'beer brewer'.
Brouwer
* Adriaen Brouwer (1605–1638), Flemish painter
* Alexander Brouwer (b. 1989), Dutch beach volleyball player
* Andries Bro ...
, who promoted intuitionistic logic, which explicitly lacks the law of excluded middle.
These problems and debates led to a wide expansion of mathematical logic, with subareas such as model theory
In mathematical logic, model theory is the study of the relationship between formal theories (a collection of sentences in a formal language expressing statements about a mathematical structure), and their models (those structures in which the s ...
(modeling some logical theories inside other theories), proof theory
Proof theory is a major branchAccording to Wang (1981), pp. 3–4, proof theory is one of four domains mathematical logic, together with model theory, axiomatic set theory, and recursion theory. Jon Barwise, Barwise (1978) consists of four correspo ...
, type theory, computability theory
Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since e ...
and computational complexity theory. Although these aspects of mathematical logic were introduced before the rise of computer
A computer is a machine that can be programmed to Execution (computing), carry out sequences of arithmetic or logical operations (computation) automatically. Modern digital electronic computers can perform generic sets of operations known as C ...
s, their use in compiler
In computing, a compiler is a computer program that translates computer code written in one programming language (the ''source'' language) into another language (the ''target'' language). The name "compiler" is primarily used for programs that ...
design, program certification, proof assistants and other aspects of computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includin ...
, contributed in turn to the expansion of these logical theories.
Statistics and other decision sciences
 The field of statistics is a mathematical application that is employed for the collection and processing of data samples, using procedures based on mathematical methods especially probability theory. Statisticians generate data with random sampling or randomized experiments. The design of a statistical sample or experiment determines the analytical methods that will be used. Analysis of data from observational studies is done using
The field of statistics is a mathematical application that is employed for the collection and processing of data samples, using procedures based on mathematical methods especially probability theory. Statisticians generate data with random sampling or randomized experiments. The design of a statistical sample or experiment determines the analytical methods that will be used. Analysis of data from observational studies is done using statistical model
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of Sample (statistics), sample data (and similar data from a larger Statistical population, population). A statistical model repres ...
s and the theory of inference
Inferences are steps in reasoning, moving from premises to logical consequences; etymologically, the word '' infer'' means to "carry forward". Inference is theoretically traditionally divided into deduction and induction, a distinction that in ...
, using model selection and estimation. The models and consequential predictions should then be tested against new data.
Statistical theory studies decision problems
In computability theory and computational complexity theory, a decision problem is a computational problem that can be posed as a yes–no question of the input values. An example of a decision problem is deciding by means of an algorithm whethe ...
such as minimizing the risk (expected loss Expected loss is the sum of the values of all possible losses, each multiplied by the probability of that loss occurring.
In bank lending (homes, autos, credit cards, commercial lending, etc.) the expected loss on a loan varies over time for a nu ...
) of a statistical action, such as using a procedure
Procedure may refer to:
* Medical procedure
* Instructions or recipes, a set of commands that show how to achieve some result, such as to prepare or make something
* Procedure (business), specifying parts of a business process
* Standard operat ...
in, for example, parameter estimation, hypothesis testing, and selecting the best. In these traditional areas of mathematical statistics, a statistical-decision problem is formulated by minimizing an objective function, like expected loss or cost, under specific constraints. For example, designing a survey often involves minimizing the cost of estimating a population mean with a given level of confidence. Because of its use of optimization, the mathematical theory of statistics overlaps with other decision sciences, such as operations research, control theory, and mathematical economics
Mathematical economics is the application of mathematical methods to represent theories and analyze problems in economics. Often, these applied methods are beyond simple geometry, and may include differential and integral calculus, difference an ...
.
Computational mathematics
Computational mathematics is the study ofmathematical problem
A mathematical problem is a problem that can be represented, analyzed, and possibly solved, with the methods of mathematics. This can be a real-world problem, such as computing the orbits of the planets in the solar system, or a problem of a more ...
s that are typically too large for human, numerical capacity. Numerical analysis studies methods for problems in analysis using functional analysis and approximation theory
In mathematics, approximation theory is concerned with how function (mathematics), functions can best be approximation, approximated with simpler functions, and with quantitative property, quantitatively characterization (mathematics), characteri ...
; numerical analysis broadly includes the study of approximation
An approximation is anything that is intentionally similar but not exactly equality (mathematics), equal to something else.
Etymology and usage
The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very ...
and discretization
In applied mathematics, discretization is the process of transferring continuous functions, models, variables, and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical ...
with special focus on rounding errors. Numerical analysis and, more broadly, scientific computing also study non-analytic topics of mathematical science, especially algorithmic-matrix
Matrix most commonly refers to:
* ''The Matrix'' (franchise), an American media franchise
** '' The Matrix'', a 1999 science-fiction action film
** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchi ...
-and- graph theory. Other areas of computational mathematics include computer algebra
In mathematics and computer science, computer algebra, also called symbolic computation or algebraic computation, is a scientific area that refers to the study and development of algorithms and software for manipulating mathematical expressions ...
and symbolic computation
In mathematics and computer science, computer algebra, also called symbolic computation or algebraic computation, is a scientific area that refers to the study and development of algorithms and software for manipulating mathematical expressions ...
.
History
Ancient
The history of mathematics is an ever-growing series of abstractions. Evolutionarily speaking, the first abstraction to ever be discovered, one shared by many animals, was probably that of numbers: the realization that, for example, a collection of two apples and a collection of two oranges (say) have something in common, namely that there are of them. As evidenced by tallies found on bone, in addition to recognizing how tocount
Count (feminine: countess) is a historical title of nobility in certain European countries, varying in relative status, generally of middling rank in the hierarchy of nobility. Pine, L. G. ''Titles: How the King Became His Majesty''. New Yor ...
physical objects, prehistoric
Prehistory, also known as pre-literary history, is the period of human history between the use of the first stone tools by hominins 3.3 million years ago and the beginning of recorded history with the invention of writing systems. The use of ...
peoples may have also known how to count abstract quantities, like timedays, seasons, or years.
 Evidence for more complex mathematics does not appear until around 3000 , when the
Evidence for more complex mathematics does not appear until around 3000 , when the Babylonia
Babylonia (; Akkadian: , ''māt Akkadī'') was an ancient Akkadian-speaking state and cultural area based in the city of Babylon in central-southern Mesopotamia (present-day Iraq and parts of Syria). It emerged as an Amorite-ruled state c. ...
ns and Egyptians began using arithmetic, algebra, and geometry for taxation and other financial calculations, for building and construction, and for astronomy. The oldest mathematical texts from Mesopotamia and Egypt
Egypt ( ar, مصر , ), officially the Arab Republic of Egypt, is a transcontinental country spanning the northeast corner of Africa and southwest corner of Asia via a land bridge formed by the Sinai Peninsula. It is bordered by the Med ...
are from 2000 to 1800 BC. Many early texts mention Pythagorean triples and so, by inference, the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
seems to be the most ancient and widespread mathematical concept after basic arithmetic and geometry. It is in Babylonian mathematics that elementary arithmetic (addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol ) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication and Division (mathematics), division. ...
, subtraction
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, . For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken ...
,