|
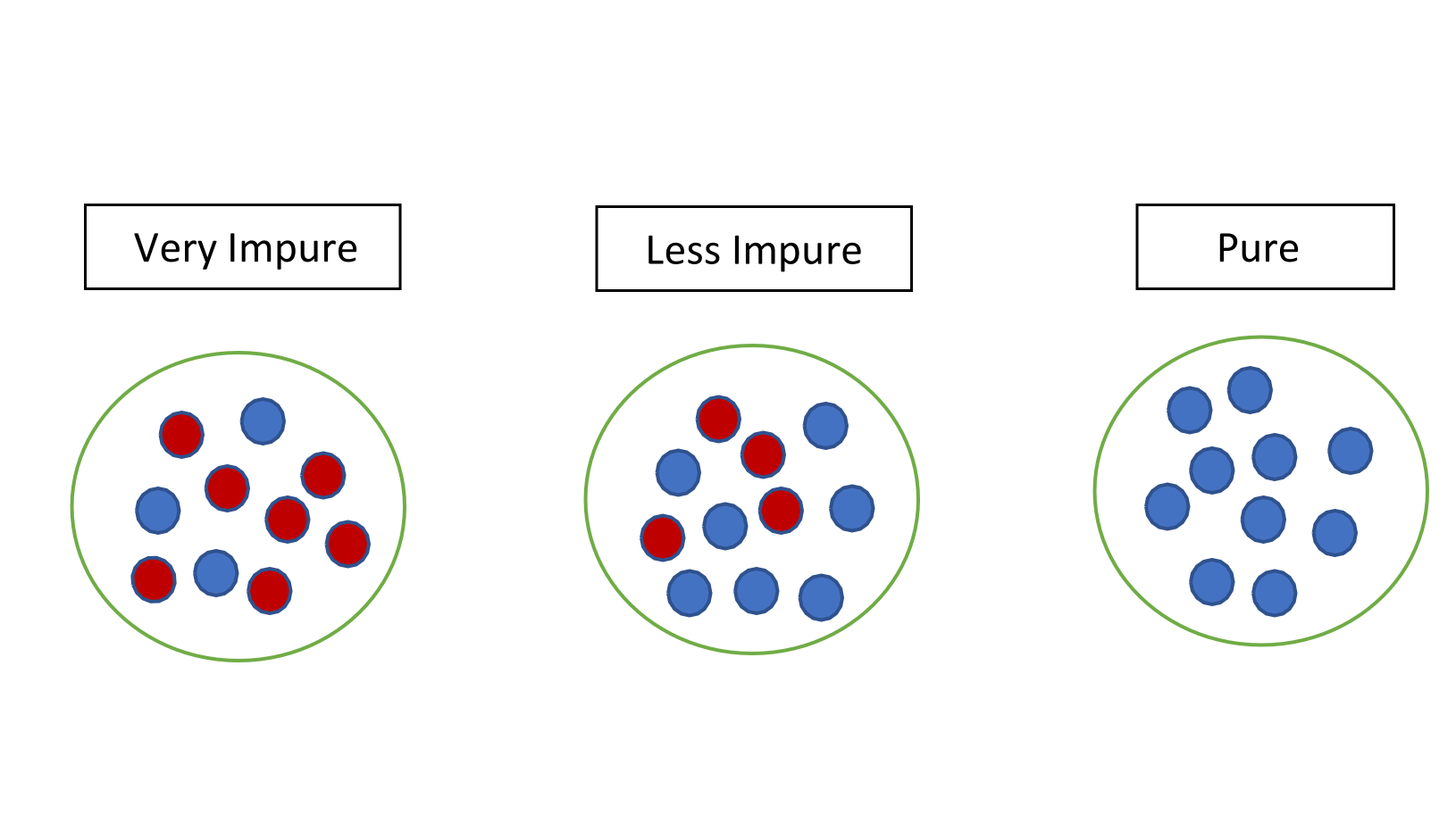
Information Gain In Decision Trees
In information theory and machine learning, information gain is a synonym for ''Kullback–Leibler divergence''; the amount of information gained about a random variable or signal from observing another random variable. However, in the context of decision trees, the term is sometimes used synonymously with mutual information, which is the conditional expected value of the Kullback–Leibler divergence of the univariate probability distribution of one variable from the conditional distribution of this variable given the other one. The information gain of a random variable ''X'' obtained from an observation of a random variable ''A'' taking value is defined IG_ = D_\text, the Kullback–Leibler divergence of the prior distribution P_ for x from the posterior distribution P_ for ''x'' given ''a''. The expected value of the information gain is the mutual information of ''X'' and ''A'' – i.e. the reduction in the entropy of ''X'' achieved by learning the state of the random v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the scientific study of the quantification, storage, and communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering, and electrical engineering. A key measure in information theory is entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a die (with six equally likely outcomes). Some other important measures in information theory are mutual information, channel capacity, error exponents, and relative entropy. Important sub-fields of information theory include s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expectation Value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with also often stylized as or \mathbb. History The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes ''in a fair way'' between two players, who have to end t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiley (publisher)
John Wiley & Sons, Inc., commonly known as Wiley (), is an American multinational publishing company founded in 1807 that focuses on academic publishing and instructional materials. The company produces books, journals, and encyclopedias, in print and electronically, as well as online products and services, training materials, and educational materials for undergraduate, graduate, and continuing education students. History The company was established in 1807 when Charles Wiley opened a print shop in Manhattan. The company was the publisher of 19th century American literary figures like James Fenimore Cooper, Washington Irving, Herman Melville, and Edgar Allan Poe, as well as of legal, religious, and other non-fiction titles. The firm took its current name in 1865. Wiley later shifted its focus to scientific, technical, and engineering subject areas, abandoning its literary interests. Wiley's son John (born in Flatbush, New York, October 4, 1808; died in East Orange, New ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analogy
Analogy (from Greek language, Greek ''analogia'', "proportion", from ''ana-'' "upon, according to" [also "against", "anew"] + ''logos'' "ratio" [also "word, speech, reckoning"]) is a cognition, cognitive process of transferring information or Meaning (linguistics), meaning from a particular subject (the analog, or source) to another (the target), or a language, linguistic expression corresponding to such a process. In a narrower sense, analogy is an inference or an Logical argument, argument from one particular to another particular, as opposed to deductive reasoning, deduction, inductive reasoning, induction, and abductive reasoning, abduction, in which at least one of the premises, or the conclusion, is general rather than particular in nature. The term analogy can also refer to the relation between the source and the target themselves, which is often (though not always) a Similarity (philosophy), similarity, as in the analogy (biology), biological notion of analogy. Analogy pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Distribution
In probability theory and statistics, a categorical distribution (also called a generalized Bernoulli distribution, multinoulli distribution) is a discrete probability distribution that describes the possible results of a random variable that can take on one of ''K'' possible categories, with the probability of each category separately specified. There is no innate underlying ordering of these outcomes, but numerical labels are often attached for convenience in describing the distribution, (e.g. 1 to ''K''). The ''K''-dimensional categorical distribution is the most general distribution over a ''K''-way event; any other discrete distribution over a size-''K'' sample space is a special case. The parameters specifying the probabilities of each possible outcome are constrained only by the fact that each must be in the range 0 to 1, and all must sum to 1. The categorical distribution is the generalization of the Bernoulli distribution for a categorical random variable, i.e. for a di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, set ''A'' is a subset of a set ''B'' if all elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. The subset relation defines a partial order on sets. In fact, the subsets of a given set form a Boolean algebra under the subset relation, in which the join and meet are given by intersection and union, and the subset relation itself is the Boolean inclusion relation. Definition If ''A'' and ''B'' are sets and every element of ''A'' is also an element of ''B'', then: :*''A'' is a subset of ''B'', denoted by A \subseteq B, or equivalently, :* ''B'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjoint Sets
In mathematics, two sets are said to be disjoint sets if they have no element in common. Equivalently, two disjoint sets are sets whose intersection is the empty set.. For example, and are ''disjoint sets,'' while and are not disjoint. A collection of two or more sets is called disjoint if any two distinct sets of the collection are disjoint. Generalizations This definition of disjoint sets can be extended to a family of sets \left(A_i\right)_: the family is pairwise disjoint, or mutually disjoint if A_i \cap A_j = \varnothing whenever i \neq j. Alternatively, some authors use the term disjoint to refer to this notion as well. For families the notion of pairwise disjoint or mutually disjoint is sometimes defined in a subtly different manner, in that repeated identical members are allowed: the family is pairwise disjoint if A_i \cap A_j = \varnothing whenever A_i \neq A_j (every two ''distinct'' sets in the family are disjoint).. For example, the collection of sets is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Of A Set
In mathematics, a partition of a set is a grouping of its elements into non-empty subsets, in such a way that every element is included in exactly one subset. Every equivalence relation on a set defines a partition of this set, and every partition defines an equivalence relation. A set equipped with an equivalence relation or a partition is sometimes called a setoid, typically in type theory and proof theory. Definition and Notation A partition of a set ''X'' is a set of non-empty subsets of ''X'' such that every element ''x'' in ''X'' is in exactly one of these subsets (i.e., ''X'' is a disjoint union of the subsets). Equivalently, a family of sets ''P'' is a partition of ''X'' if and only if all of the following conditions hold: *The family ''P'' does not contain the empty set (that is \emptyset \notin P). *The union of the sets in ''P'' is equal to ''X'' (that is \textstyle\bigcup_ A = X). The sets in ''P'' are said to exhaust or cover ''X''. See also collectively ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Classification
In statistics, classification is the problem of identifying which of a set of categories (sub-populations) an observation (or observations) belongs to. Examples are assigning a given email to the "spam" or "non-spam" class, and assigning a diagnosis to a given patient based on observed characteristics of the patient (sex, blood pressure, presence or absence of certain symptoms, etc.). Often, the individual observations are analyzed into a set of quantifiable properties, known variously as explanatory variables or ''features''. These properties may variously be categorical (e.g. "A", "B", "AB" or "O", for blood type), ordinal (e.g. "large", "medium" or "small"), integer-valued (e.g. the number of occurrences of a particular word in an email) or real-valued (e.g. a measurement of blood pressure). Other classifiers work by comparing observations to previous observations by means of a similarity or distance function. An algorithm that implements classification, especially in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
A set is the mathematical model for a collection of different things; a set contains ''elements'' or ''members'', which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other sets. The set with no element is the empty set; a set with a single element is a singleton. A set may have a finite number of elements or be an infinite set. Two sets are equal if they have precisely the same elements. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. History The concept of a set emerged in mathematics at the end of the 19th century. The German word for set, ''Menge'', was coined by Bernard Bolzano in his work '' Paradoxes of the Infinite''. Georg Cantor, one of the founders of set theory, gave the following ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shannon Entropy
Shannon may refer to: People * Shannon (given name) * Shannon (surname) * Shannon (American singer), stage name of singer Shannon Brenda Greene (born 1958) * Shannon (South Korean singer), British-South Korean singer and actress Shannon Arrum Williams (born 1998) * Shannon, intermittent stage name of English singer-songwriter Marty Wilde (born 1939) * Claude Shannon (1916-2001) was American mathematician, electrical engineer, and cryptographer known as a "father of information theory" Places Australia * Shannon, Tasmania, a locality * Hundred of Shannon, a cadastral unit in South Australia * Shannon, a former name for the area named Calomba, South Australia since 1916 * Shannon River (Western Australia) Canada * Shannon, New Brunswick, a community * Shannon, Quebec, a city * Shannon Bay, former name of Darrell Bay, British Columbia * Shannon Falls, a waterfall in British Columbia Ireland * River Shannon, the longest river in Ireland ** Shannon Cave, a subterranean section ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feature Vector
In machine learning and pattern recognition, a feature is an individual measurable property or characteristic of a phenomenon. Choosing informative, discriminating and independent features is a crucial element of effective algorithms in pattern recognition, classification and regression. Features are usually numeric, but structural features such as strings and graphs are used in syntactic pattern recognition. The concept of "feature" is related to that of explanatory variable used in statistical techniques such as linear regression. Classification A numeric feature can be conveniently described by a feature vector. One way to achieve binary classification is using a linear predictor function (related to the perceptron) with a feature vector as input. The method consists of calculating the scalar product between the feature vector and a vector of weights, qualifying those observations whose result exceeds a threshold. Algorithms for classification from a feature vec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |