|
Bayesian Experimental Design
Bayesian experimental design provides a general probability-theoretical framework from which other theories on experimental design can be derived. It is based on Bayesian inference to interpret the observations/data acquired during the experiment. This allows accounting for both any prior knowledge on the parameters to be determined as well as uncertainties in observations. The theory of Bayesian experimental design is to a certain extent based on the theory for making optimal decisions under uncertainty. The aim when designing an experiment is to maximize the expected utility of the experiment outcome. The utility is most commonly defined in terms of a measure of the accuracy of the information provided by the experiment (e.g., the Shannon information or the negative of the variance) but may also involve factors such as the financial cost of performing the experiment. What will be the optimal experiment design depends on the particular utility criterion chosen. Relations to more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Design Of Experiments
The design of experiments (DOE), also known as experiment design or experimental design, is the design of any task that aims to describe and explain the variation of information under conditions that are hypothesized to reflect the variation. The term is generally associated with experiments in which the design introduces conditions that directly affect the variation, but may also refer to the design of quasi-experiments, in which natural conditions that influence the variation are selected for observation. In its simplest form, an experiment aims at predicting the outcome by introducing a change of the preconditions, which is represented by one or more independent variables, also referred to as "input variables" or "predictor variables." The change in one or more independent variables is generally hypothesized to result in a change in one or more dependent variables, also referred to as "output variables" or "response variables." The experimental design may also identify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
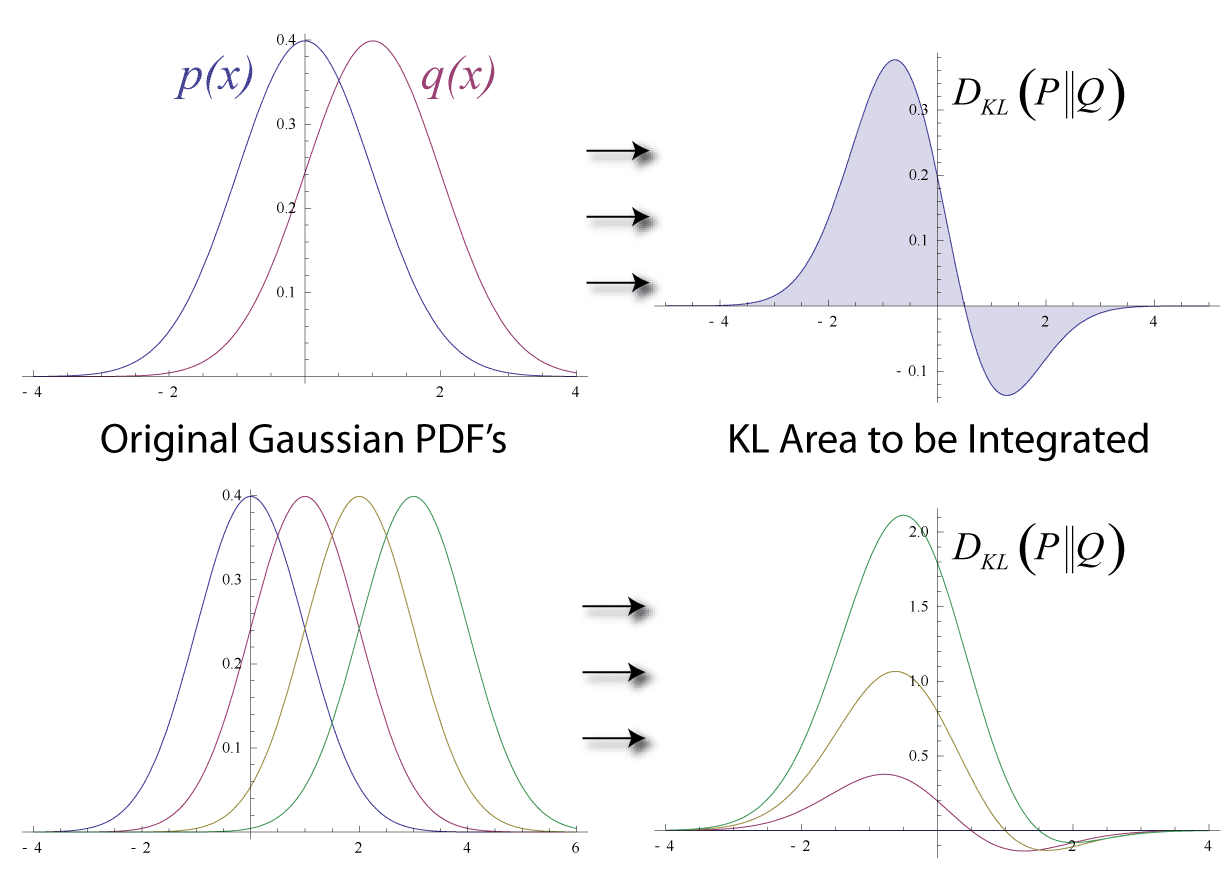
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimal Decisions
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Optimization problems can be divided into two categories, depending on whether the variables ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Statistics
Bayesian statistics ( or ) is a theory in the field of statistics based on the Bayesian interpretation of probability, where probability expresses a ''degree of belief'' in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation, which views probability as the limit of the relative frequency of an event after many trials. More concretely, analysis in Bayesian methods codifies prior knowledge in the form of a prior distribution. Bayesian statistical methods use Bayes' theorem to compute and update probabilities after obtaining new data. Bayes' theorem describes the conditional probability of an event based on data as well as prior information or beliefs about the event or conditions related to the event. For example, in Bayesian inference, Bayes' theorem can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calyampudi Radhakrishna Rao
Prof. Calyampudi Radhakrishna Rao (10 September 1920 – 22 August 2023) was an Indian-American mathematician and statistician. He was professor emeritus at Pennsylvania State University and research professor at the University at Buffalo. Rao was honoured by numerous colloquia, honorary degrees, and festschrifts and was awarded the US National Medal of Science in 2002. The American Statistical Association has described him as "a living legend" whose work has influenced not just statistics, but has had far reaching implications for fields as varied as economics, genetics, anthropology, geology, national planning, demography, biometry, and medicine." ''The Times of India'' listed Rao as one of the top 10 Indian scientists of all time. In 2023, Rao was awarded the International Prize in Statistics, an award often touted as the "statistics' equivalent of the Nobel Prize". Rao was also a Senior Policy and Statistics advisor for the Indian Heart Association non-profit focused on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
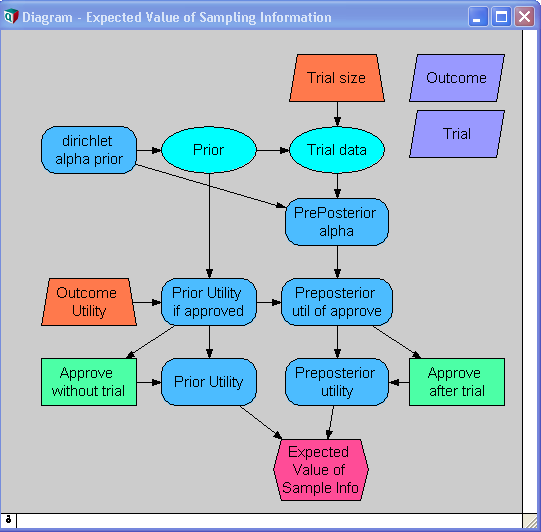
Expected Value Of Sample Information
In decision theory, the expected value of sample information (EVSI) is the expected increase in utility that a decision-maker could obtain from gaining access to a sample of additional observations before making a decision. The additional information obtained from the sample may allow them to make a more informed, and thus better, decision, thus resulting in an increase in expected utility. EVSI attempts to estimate what this improvement would be before seeing actual sample data; hence, EVSI is a form of what is known as ''preposterior analysis''. The use of EVSI in decision theory was popularized by Robert Schlaifer and Howard Raiffa in the 1960s. Formulation Let : \begin d\in D & \mbox D \\ x\in X & \mbox X \\ z \in Z & \mbox n \mbox \langle z_1,z_2,..,z_n \rangle \\ U(d,x) & \mbox d \mbox x \\ p(x) & \mbox x \\ p(z, x) & \mbox z \end It is common (but not essential) in EVSI scenarios for Z_i=X, p(z, x)=\prod p(z_i, x) and \int z p(z, x) dz = x, which is to say that each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Active Learning (machine Learning)
Active learning is a special case of machine learning in which a learning algorithm can interactively query a human user (or some other information source), to label new data points with the desired outputs. The human user must possess knowledge/expertise in the problem domain, including the ability to consult/research authoritative sources when necessary. In statistics literature, it is sometimes also called optimal experimental design. The information source is also called ''teacher'' or ''oracle''. There are situations in which unlabeled data is abundant but manual labeling is expensive. In such a scenario, learning algorithms can actively query the user/teacher for labels. This type of iterative supervised learning is called active learning. Since the learner chooses the examples, the number of examples to learn a concept can often be much lower than the number required in normal supervised learning. With this approach, there is a risk that the algorithm is overwhelmed by un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimal Design
In the design of experiments, optimal experimental designs (or optimum designs) are a class of experimental designs that are optimal with respect to some statistical criterion. The creation of this field of statistics has been credited to Danish statistician Kirstine Smith. In the design of experiments for estimating statistical models, optimal designs allow parameters to be estimated without bias and with minimum variance. A non-optimal design requires a greater number of experimental runs to estimate the parameters with the same precision as an optimal design. In practical terms, optimal experiments can reduce the costs of experimentation. The optimality of a design depends on the statistical model and is assessed with respect to a statistical criterion, which is related to the variance-matrix of the estimator. Specifying an appropriate model and specifying a suitable criterion function both require understanding of statistical theory and practical knowledge with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Optimization
Bayesian optimization is a sequential design strategy for global optimization of black-box functions, that does not assume any functional forms. It is usually employed to optimize expensive-to-evaluate functions. With the rise of artificial intelligence innovation in the 21st century, Bayesian optimizations have found prominent use in machine learning problems for optimizing hyperparameter values. History The term is generally attributed to and is coined in his work from a series of publications on global optimization in the 1970s and 1980s. Early mathematics foundations From 1960s to 1980s The earliest idea of Bayesian optimization sprang in 1964, from a paper by American applied mathematician Harold J. Kushner“A New Method of Locating the Maximum Point of an Arbitrary Multipeak Curve in the Presence of Noise” Although not directly proposing Bayesian optimization, in this paper, he first proposed a new method of locating the maximum point of an arbitrary multipeak curv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gambling And Information Theory
Statistical inference might be thought of as gambling theory applied to the world around us. The myriad applications for logarithmic information measures tell us precisely how to take the best guess in the face of partial information. In that sense, information theory might be considered a formal expression of the theory of gambling. It is no surprise, therefore, that information theory has applications to games of chance. Kelly Betting Kelly betting or proportional betting is an application of information theory to investing and gambling. Its discoverer was John Larry Kelly, Jr. Part of Kelly's insight was to have the gambler maximize the expectation of the ''logarithm'' of his capital, rather than the expected profit from each bet. This is important, since in the latter case, one would be led to gamble all he had when presented with a favorable bet, and if he lost, would have no capital with which to place subsequent bets. Kelly realized that it was the logarithm of the ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kelly Criterion
In probability theory, the Kelly criterion (or Kelly strategy or Kelly bet) is a formula for sizing a sequence of bets by maximizing the long-term expected value of the logarithm of wealth, which is equivalent to maximizing the long-term expected Geometric mean, geometric growth rate. John Larry Kelly Jr., a researcher at Bell Labs, described the criterion in 1956. The practical use of the formula has been demonstrated for gambling, and the same idea was used to explain Diversification (finance), diversification in investment management., page 184f. In the 2000s, Kelly-style analysis became a part of mainstream investment theory and the claim has been made that well-known successful investors including Warren Buffett and William H. Gross, Bill Gross use Kelly methods. Also see intertemporal portfolio choice. It is also the standard replacement of Power of a test, statistical power in anytime-valid statistical tests and confidence intervals, based on E-values, e-values and e-proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual Statistical dependence, dependence between the two variables. More specifically, it quantifies the "Information content, amount of information" (in Units of information, units such as shannon (unit), shannons (bits), Nat (unit), nats or Hartley (unit), hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of Entropy (information theory), entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the Pearson correlation coefficient, correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |