Bivector on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 The rotation vector is an example of an
The rotation vector is an example of an
 As suggested by their name and that of the algebra, one of the attractions of bivectors is that they have a natural geometric interpretation. This can be described in any dimension but is best done in three where parallels can be drawn with more familiar objects, before being applied to higher dimensions. In two dimensions the geometric interpretation is trivial, as the space is two-dimensional so has only one plane, and all bivectors are associated with it differing only by a scale factor.
All bivectors can be interpreted as
As suggested by their name and that of the algebra, one of the attractions of bivectors is that they have a natural geometric interpretation. This can be described in any dimension but is best done in three where parallels can be drawn with more familiar objects, before being applied to higher dimensions. In two dimensions the geometric interpretation is trivial, as the space is two-dimensional so has only one plane, and all bivectors are associated with it differing only by a scale factor.
All bivectors can be interpreted as  In three dimensions all bivectors can be generated by the exterior product of two vectors. If the bivector then the magnitude of B is
:
where ''θ'' is the angle between the vectors. This is the area of the
In three dimensions all bivectors can be generated by the exterior product of two vectors. If the bivector then the magnitude of B is
:
where ''θ'' is the angle between the vectors. This is the area of the  This relates the
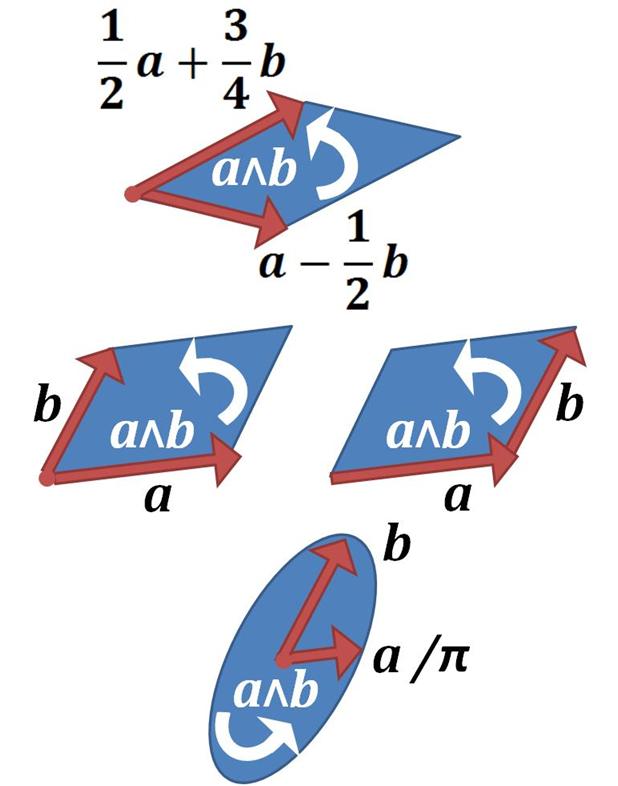
This relates the  Bivectors can be added together as areas. Given two non-zero bivectors B and C in three dimensions it is always possible to find a vector that is contained in both, a say, so the bivectors can be written as exterior products involving a:
:
This can be interpreted geometrically as seen in the diagram: the two areas sum to give a third, with the three areas forming faces of a
Bivectors can be added together as areas. Given two non-zero bivectors B and C in three dimensions it is always possible to find a vector that is contained in both, a say, so the bivectors can be written as exterior products involving a:
:
This can be interpreted geometrically as seen in the diagram: the two areas sum to give a third, with the three areas forming faces of a
 The rotations generated are more complex though. They can be categorised as follows:
: ''
The rotations generated are more complex though. They can be categorised as follows:
: ''
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, a bivector or 2-vector is a quantity in exterior algebra
In mathematics, the exterior algebra, or Grassmann algebra, named after Hermann Grassmann, is an algebra that uses the exterior product or wedge product as its multiplication. In mathematics, the exterior product or wedge product of vectors is ...
or geometric algebra
In mathematics, a geometric algebra (also known as a real Clifford algebra) is an extension of elementary algebra to work with geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the ge ...
that extends the idea of scalar
Scalar may refer to:
*Scalar (mathematics), an element of a field, which is used to define a vector space, usually the field of real numbers
* Scalar (physics), a physical quantity that can be described by a single element of a number field such ...
s and vector
Vector most often refers to:
*Euclidean vector, a quantity with a magnitude and a direction
*Vector (epidemiology), an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematic ...
s. If a scalar is considered a degree-zero quantity, and a vector is a degree-one quantity, then a bivector can be thought of as being of degree two. Bivectors have applications in many areas of mathematics and physics. They are related to complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
s in two dimensions and to both pseudovector
In physics and mathematics, a pseudovector (or axial vector) is a quantity that is defined as a function of some vectors or other geometric shapes, that resembles a vector, and behaves like a vector in many situations, but is changed into its o ...
s and quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quatern ...
s in three dimensions. They can be used to generate rotation
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional ...
s in any number of dimensions, and are a useful tool for classifying such rotations. They are also used in physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
, tying together a number of otherwise unrelated quantities.
Bivectors are generated by the exterior product
In mathematics, specifically in topology,
the interior of a subset of a topological space is the union of all subsets of that are open in .
A point that is in the interior of is an interior point of .
The interior of is the complement of the ...
on vectors: given two vectors a and b, their exterior product is a bivector, as is the sum of any bivectors. Not all bivectors can be generated as a single exterior product. More precisely, a bivector that can be expressed as an exterior product is called ''simple''; in up to three dimensions all bivectors are simple, but in higher dimensions this is not the case. The exterior product of two vectors is alternating, so is the negation of the bivector , producing the opposite orientation, and is the zero bivector.
Geometrically, a simple bivector can be interpreted as an oriented plane
Plane(s) most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
Plane or planes may also refer to:
Biology
* Plane (tree) or ''Platanus'', wetland native plant
* Planes (gen ...
segment, much as vector
Vector most often refers to:
*Euclidean vector, a quantity with a magnitude and a direction
*Vector (epidemiology), an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematic ...
s can be thought of as directed line segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between ...
s.
The bivector has a ''magnitude'' equal to the area of the parallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equa ...
with edges a and b, has the ''attitude'' of the plane spanned by a and b, and has ''orientation'' being the sense of the rotation that would align a with b.
In layman terms, any surface is the same bivector, if it has the same area, same orientation, and is parallel to the same plane (see figure).
History
The bivector was first defined in 1844 by German mathematicianHermann Grassmann
Hermann Günther Grassmann (german: link=no, Graßmann, ; 15 April 1809 – 26 September 1877) was a German polymath known in his day as a linguist and now also as a mathematician. He was also a physicist, general scholar, and publisher. His mat ...
in exterior algebra
In mathematics, the exterior algebra, or Grassmann algebra, named after Hermann Grassmann, is an algebra that uses the exterior product or wedge product as its multiplication. In mathematics, the exterior product or wedge product of vectors is ...
as the result of the exterior product
In mathematics, specifically in topology,
the interior of a subset of a topological space is the union of all subsets of that are open in .
A point that is in the interior of is an interior point of .
The interior of is the complement of the ...
of two vectors. Just the previous year, in Ireland, William Rowan Hamilton
Sir William Rowan Hamilton Doctor of Law, LL.D, Doctor of Civil Law, DCL, Royal Irish Academy, MRIA, Royal Astronomical Society#Fellow, FRAS (3/4 August 1805 – 2 September 1865) was an Irish mathematician, astronomer, and physicist. He was the ...
had discovered quaternions
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quatern ...
. Hamilton coined both ''vector'' and ''bivector'', the latter in his ''Lectures on Quaternions'' (1853) as he introduced biquaternion
In abstract algebra, the biquaternions are the numbers , where , and are complex numbers, or variants thereof, and the elements of multiply as in the quaternion group and commute with their coefficients. There are three types of biquaternions co ...
s which have bivector In mathematics, a bivector or 2-vector is a quantity in exterior algebra or geometric algebra that extends the idea of scalar (mathematics), scalars and Euclidean vector, vectors. If a scalar is considered a degree-zero quantity, and a vector is a d ...
s for their vector parts. It was not until English mathematician William Kingdon Clifford
William Kingdon Clifford (4 May 18453 March 1879) was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his ...
in 1888 added the geometric product to Grassmann's algebra, incorporating the ideas of both Hamilton and Grassmann, and founded Clifford algebra
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra. As -algebras, they generalize the real numbers, complex numbers, quaternions and several other hyperc ...
, that the bivector of this article arose. Henry Forder
Henry George Forder (27 September 1889 – 21 September 1981) was a New Zealand mathematician.
Academic career
Born in Shotesham All Saints, near Norwich, he won a scholarships first to a Grammar school and then to University of Cambridge. Af ...
used the term ''bivector'' to develop exterior algebra in 1941.
In the 1890s Josiah Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in t ...
and Oliver Heaviside
Oliver Heaviside FRS (; 18 May 1850 – 3 February 1925) was an English self-taught mathematician and physicist who invented a new technique for solving differential equations (equivalent to the Laplace transform), independently developed vec ...
developed vector calculus
Vector calculus, or vector analysis, is concerned with differentiation and integration of vector fields, primarily in 3-dimensional Euclidean space \mathbb^3. The term "vector calculus" is sometimes used as a synonym for the broader subject ...
, which included separate cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is ...
and dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebra ...
s that were derived from quaternion multiplication.A discussion of quaternions from these years is at:– The success of vector calculus, and of the book ''Vector Analysis
Vector calculus, or vector analysis, is concerned with derivative, differentiation and integral, integration of vector fields, primarily in 3-dimensional Euclidean space \mathbb^3. The term "vector calculus" is sometimes used as a synonym for ...
'' by Gibbs and Wilson
Wilson may refer to:
People
* Wilson (name)
** List of people with given name Wilson
** List of people with surname Wilson
* Wilson (footballer, 1927–1998), Brazilian manager and defender
* Wilson (footballer, born 1984), full name Wilson Ro ...
, had the effect that the insights of Hamilton and Clifford were overlooked for a long time, since much of 20th century mathematics and physics was formulated in vector terms. Gibbs used vectors to fill the role of bivectors in three dimensions, and used bivector In mathematics, a bivector or 2-vector is a quantity in exterior algebra or geometric algebra that extends the idea of scalar (mathematics), scalars and Euclidean vector, vectors. If a scalar is considered a degree-zero quantity, and a vector is a d ...
in Hamilton's sense, a use that has sometimes been copied.
Today the bivector is largely studied as a topic in geometric algebra
In mathematics, a geometric algebra (also known as a real Clifford algebra) is an extension of elementary algebra to work with geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the ge ...
, a Clifford algebra over real
Real may refer to:
Currencies
* Brazilian real (R$)
* Central American Republic real
* Mexican real
* Portuguese real
* Spanish real
* Spanish colonial real
Music Albums
* ''Real'' (L'Arc-en-Ciel album) (2000)
* ''Real'' (Bright album) (2010)
...
or complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
vector space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called ''vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but can ...
s with a quadratic form
In mathematics, a quadratic form is a polynomial with terms all of degree two ("form" is another name for a homogeneous polynomial). For example,
:4x^2 + 2xy - 3y^2
is a quadratic form in the variables and . The coefficients usually belong to a ...
. Its resurgence was led by David Hestenes
David Orlin Hestenes (born May 21, 1933) is a theoretical physicist and science educator. He is best known as chief architect of geometric algebra as a unified language for mathematics and physics, and as founder of Modelling Instructio ...
who, along with others, applied geometric algebra to a range of new applications in physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
.
Derivation
For this article the bivector will be considered only in real geometric algebras. This in practice is not much of a restriction, as all useful applications are drawn from such algebras. Also unless otherwise stated, all examples have aEuclidean metric
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points.
It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore oc ...
and so a positive-definite In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive-definite. See, in particular:
* Positive-definite bilinear form
* Positive-definite fu ...
quadratic form
In mathematics, a quadratic form is a polynomial with terms all of degree two ("form" is another name for a homogeneous polynomial). For example,
:4x^2 + 2xy - 3y^2
is a quadratic form in the variables and . The coefficients usually belong to a ...
.
Geometric algebra and the geometric product
The bivector arises from the definition of the geometric product over a vector space. For vectors a, b and c, the geometric product on vectors is defined as follows: ;Associativity
In mathematics, the associative property is a property of some binary operations, which means that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement f ...
:
;Left and right distributivity
In mathematics, the distributive property of binary operations generalizes the distributive law, which asserts that the equality
x \cdot (y + z) = x \cdot y + x \cdot z
is always true in elementary algebra.
For example, in elementary arithmetic, ...
:
;Contraction: Where ''Q'' is the quadratic form, , a, is the magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
of a and ''ϵ''a is the metric signature
In mathematics, the signature of a metric tensor ''g'' (or equivalently, a real quadratic form thought of as a real symmetric bilinear form on a finite-dimensional vector space) is the number (counted with multiplicity) of positive, negative an ...
. For a space with Euclidean metric ''ϵ''a is 1 so can be omitted, and the contraction condition becomes:
The scalar product
From associativity, , is a scalar times b. When b is not parallel to and hence not a scalar multiple of a, ab cannot be a scalar. But : is a sum of scalars and so a scalar. From thelaw of cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states ...
on the triangle formed by the vectors its value is , where ''θ'' is the angle between the vectors. It is therefore identical to the scalar product between two vectors, and is written the same way,
:
It is symmetric, scalar-valued, and can be used to determine the angle between two vectors: in particular if a and b are orthogonal the product is zero.
The exterior product
Just as the scalar product can be formulated as the symmetric part of the geometric product of another quantity, the exterior product (sometimes known as the "wedge" or "progressive" product) can be formulated as its antisymmetric part: : It is antisymmetric in a and b : and by addition: : That is, the geometric product is the sum of the symmetric scalar product and alternating exterior product. To examine the nature of , consider the formula : which using thePythagorean trigonometric identity
The Pythagorean trigonometric identity, also called simply the Pythagorean identity, is an identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one of the basic relations b ...
gives the value of
:
With a negative square it cannot be a scalar or vector quantity, so it is a new sort of object, a bivector. It has magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
, where ''θ'' is the angle between the vectors, and so is zero for parallel vectors.
To distinguish them from vectors, bivectors are written here with bold capitals, for example:
:
although other conventions are used, in particular as vectors and bivectors are both elements of the geometric algebra.
Properties
The space ⋀2R''n''
The algebra generated by the geometric product is thegeometric algebra
In mathematics, a geometric algebra (also known as a real Clifford algebra) is an extension of elementary algebra to work with geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the ge ...
over the vector space. For a Euclidean vector space it is written or Cl''n''(R), where ''n'' is the dimension of the vector space R''n''. Cl''n''(R) is both a vector space and an algebra, generated by all the products between vectors in R''n'', so it contains all vectors and bivectors. More precisely as a vector space it contains the vectors and bivectors as linear subspace
In mathematics, and more specifically in linear algebra, a linear subspace, also known as a vector subspaceThe term ''linear subspace'' is sometimes used for referring to flats and affine subspaces. In the case of vector spaces over the reals, li ...
s, though not subalgebra In mathematics, a subalgebra is a subset of an algebra, closed under all its operations, and carrying the induced operations.
"Algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operat ...
s (since the geometric product of two vectors is not generally another vector). The space of all bivectors is written ⋀2R''n''.
The even subalgebra
The subalgebra generated by the bivectors is the ''even subalgebra'' of the geometric algebra, written Cl(R). This algebra results from considering all products of scalars and bivectors generated by the geometric product. It has dimension , and contains ⋀2R''n'' as a linear subspace with dimension (atriangular number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
). In two and three dimensions the even subalgebra contains only scalars and bivectors, and each is of particular interest. In two dimensions the even subalgebra is isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
to the complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
s, C, while in three it is isomorphic to the quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quatern ...
s, H. More generally the even subalgebra can be used to generate rotation
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional ...
s in any dimension, and can be generated by bivectors in the algebra.
Magnitude
As noted in the previous section the magnitude of a simple bivector, that is one that is the exterior product of two vectors a and b, is , where ''θ'' is the angle between the vectors. It is written , where B is the bivector. For general bivectors the magnitude can be calculated by taking thenorm
Naturally occurring radioactive materials (NORM) and technologically enhanced naturally occurring radioactive materials (TENORM) consist of materials, usually industrial wastes or by-products enriched with radioactive elements found in the envir ...
of the bivector considered as a vector in the space ⋀2R''n''. If the magnitude is zero then all the bivector's components are zero, and the bivector is the zero bivector which as an element of the geometric algebra equals the scalar zero.
Unit bivectors
A unit bivector is one with unit magnitude. It can be derived from any non-zero bivector by dividing the bivector by its magnitude, that is : Of particular interest are the unit bivectors formed from the products of thestandard basis
In mathematics, the standard basis (also called natural basis or canonical basis) of a coordinate vector space (such as \mathbb^n or \mathbb^n) is the set of vectors whose components are all zero, except one that equals 1. For example, in the c ...
. If e''i'' and e''j'' are distinct basis vectors then the product is a bivector. As the vectors are orthogonal this is just e''i''e''j'', written e''ij'', with unit magnitude as the vectors are unit vector
In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat").
The term ''direction vecto ...
s. The set of all such bivectors form a basis for ⋀2R''n''. For instance in four dimensions the basis for ⋀2R4 is (e1e2, e1e3, e1e4, e2e3, e2e4, e3e4) or (e12, e13, e14, e23, e24, e34).
Simple bivectors
The exterior product of two vectors is a bivector, but not all bivectors are exterior products of two vectors. For example, in four dimensions the bivector : cannot be written as the exterior product of two vectors. A bivector that can be written as the exterior product of two vectors is simple. In two and three dimensions all bivectors are simple, but not in four or more dimensions; in four dimensions every bivector is the sum of at most two exterior products. A bivector has a real square if and only if it is simple, and only simple bivectors can be represented geometrically by an oriented plane area.Product of two bivectors
The geometric product of two bivectors, A and B, is : The quantity is the scalar-valued scalar product, while is the grade 4 exterior product that arises in four or more dimensions. The quantity is the bivector-valuedcommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.
Group theory
The commutator of two elements, a ...
product, given by
:
The space of bivectors ⋀2R''n'' is a Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an Binary operation, operation called the Lie bracket, an Alternating multilinear map, alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow ...
over R, with the commutator product as the Lie bracket. The full geometric product of bivectors generates the even subalgebra.
Of particular interest is the product of a bivector with itself. As the commutator product is antisymmetric the product simplifies to
:
If the bivector is ''simple'' the last term is zero and the product is the scalar-valued , which can be used as a check for simplicity. In particular the exterior product of bivectors only exists in four or more dimensions, so all bivectors in two and three dimensions are simple.
General bivectors and Matrices
Bivectors are isomorphic toskew-symmetric matrices
In mathematics, particularly in linear algebra, a skew-symmetric (or antisymmetric or antimetric) matrix is a square matrix whose transpose equals its negative. That is, it satisfies the condition
In terms of the entries of the matrix, if a_ ...
; the general bivector maps to the matrix
:
This multiplied by vectors on both sides gives the same vector as the product of a vector and bivector minus the outer product; an example is the angular velocity tensor
In physics, angular velocity or rotational velocity ( or ), also known as angular frequency vector,(UP1) is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an obje ...
.
Skew symmetric matrices generate orthogonal matrices
In linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal vectors.
One way to express this is
Q^\mathrm Q = Q Q^\mathrm = I,
where is the transpose of and is the identity ma ...
with determinant
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and ...
1 through the exponential map. In particular, the exponent of a bivector associated with a rotation is a rotation matrix In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix
:R = \begin
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end ...
, that is the rotation matrix ''M''''R'' given by the above skew-symmetric matrix is
:
The rotation described by ''M''''R'' is the same as that described by the rotor ''R'' given by
:
and the matrix ''M''''R'' can be also calculated directly from rotor ''R'':
:
Bivectors are related to the eigenvalue
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
s of a rotation matrix. Given a rotation matrix ''M'' the eigenvalues can calculated by solving the characteristic equation for that matrix . By the fundamental theorem of algebra
The fundamental theorem of algebra, also known as d'Alembert's theorem, or the d'Alembert–Gauss theorem, states that every non- constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomial ...
this has three roots (only one of which is real as there is only one eigenvector, i.e., the axis of rotation). The other roots must be a complex conjugate pair. They have unit magnitude so purely imaginary logarithms, equal to the magnitude of the bivector associated with the rotation, which is also the angle of rotation. The eigenvectors associated with the complex eigenvalues are in the plane of the bivector, so the exterior product of two non-parallel eigenvectors results in the bivector (or a multiple thereof).
Two dimensions
When working with coordinates in geometric algebra it is usual to write thebasis vectors
In mathematics, a set of vectors in a vector space is called a basis if every element of may be written in a unique way as a finite linear combination of elements of . The coefficients of this linear combination are referred to as components ...
as (e1, e2, ...), a convention that will be used here.
A vector
Vector most often refers to:
*Euclidean vector, a quantity with a magnitude and a direction
*Vector (epidemiology), an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematic ...
in real two-dimensional space R2 can be written , where ''a''1 and ''a''2 are real numbers, e1 and e2 are orthonormal
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal (or perpendicular along a line) unit vectors. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of un ...
basis vectors. The geometric product of two such vectors is
:
This can be split into the symmetric, scalar-valued, scalar product and an antisymmetric, bivector-valued exterior product:
:
All bivectors in two dimensions are of this form, that is multiples of the bivector e1e2, written e12 to emphasise it is a bivector rather than a vector. The magnitude of e12 is 1, with
:
so it is called the unit bivector. The term unit bivector can be used in other dimensions but it is only uniquely defined (up to a sign) in two dimensions and all bivectors are multiples of e12. As the highest grade element of the algebra e12 is also the pseudoscalar
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion while a true scalar does not.
Any scalar product between a pseudovector and an ordinary vector is a pseudoscalar. The ...
which is given the symbol ''i''.
Complex numbers
With the properties of negative square and unit magnitude, the unit bivector can be identified with theimaginary unit
The imaginary unit or unit imaginary number () is a solution to the quadratic equation x^2+1=0. Although there is no real number with this property, can be used to extend the real numbers to what are called complex numbers, using addition an ...
from complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a ...
. The bivectors and scalars together form the even subalgebra of the geometric algebra, which is isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
to the complex numbers C. The even subalgebra has basis (1, e12), the whole algebra has basis (1, e1, e2, e12).
The complex numbers are usually identified with the coordinate axes
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...
and two-dimensional vectors, which would mean associating them with the vector elements of the geometric algebra. There is no contradiction in this, as to get from a general vector to a complex number an axis needs to be identified as the real axis, e1 say. This multiplies by all vectors to generate the elements of even subalgebra.
All the properties of complex numbers can be derived from bivectors, but two are of particular interest. First as with complex numbers products of bivectors and so the even subalgebra are commutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name o ...
. This is only true in two dimensions, so properties of the bivector in two dimensions that depend on commutativity do not usually generalise to higher dimensions.
Second a general bivector can be written
:
where ''θ'' is a real number. Putting this into the Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor serie ...
for the exponential map and using the property e122 = −1 results in a bivector version of Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for an ...
,
:
which when multiplied by any vector rotates it through an angle ''θ'' about the origin:
:
The product of a vector with a bivector in two dimensions is anticommutative
In mathematics, anticommutativity is a specific property of some non-commutative mathematical operations. Swapping the position of two arguments of an antisymmetric operation yields a result which is the ''inverse'' of the result with unswapped ...
, so the following products all generate the same rotation
:
Of these the last product is the one that generalises into higher dimensions. The quantity needed is called a rotor
Rotor may refer to:
Science and technology
Engineering
*Rotor (electric), the non-stationary part of an alternator or electric motor, operating with a stationary element so called the stator
* Helicopter rotor, the rotary wing(s) of a rotorcraft ...
and is given the symbol ''R'', so in two dimensions a rotor that rotates through angle ''θ'' can be written
:
and the rotation it generates is
:
Three dimensions
Inthree dimensions
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position of an element (i.e., point). This is the informal ...
the geometric product of two vectors is
:
This can be split into the symmetric, scalar-valued, scalar product and the antisymmetric, bivector-valued, exterior product:
:
In three dimensions all bivectors are simple and so the result of an exterior product. The unit bivectors e23, e31 and e12 form a basis for the space of bivectors ⋀2R3, which is itself a three-dimensional linear space. So if a general bivector is:
:
they can be added like vectors
:
while when multiplied they produce the following
:
which can be split into symmetric scalar and antisymmetric bivector parts as follows
:
The exterior product of two bivectors in three dimensions is zero.
A bivector B can be written as the product of its magnitude and a unit bivector, so writing ''β'' for , B, and using the Taylor series for the exponential map it can be shown that
:
This is another version of Euler's formula, but with a general bivector in three dimensions. Unlike in two dimensions bivectors are not commutative so properties that depend on commutativity do not apply in three dimensions. For example, in general in three (or more) dimensions.
The full geometric algebra in three dimensions, Cl3(R), has basis (1, e1, e2, e3, e23, e31, e12, e123). The element e123 is a trivector and the pseudoscalar
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion while a true scalar does not.
Any scalar product between a pseudovector and an ordinary vector is a pseudoscalar. The ...
for the geometry. Bivectors in three dimensions are sometimes identified with pseudovector
In physics and mathematics, a pseudovector (or axial vector) is a quantity that is defined as a function of some vectors or other geometric shapes, that resembles a vector, and behaves like a vector in many situations, but is changed into its o ...
s
to which they are related, as discussed below.
Quaternions
Bivectors are not closed under the geometric product, but the even subalgebra is. In three dimensions it consists of all scalar and bivector elements of the geometric algebra, so a general element can be written for example ''a'' + A, where ''a'' is the scalar part and A is the bivector part. It is written Cl and has basis (1, e23, e31, e12). The product of two general elements of the even subalgebra is : The even subalgebra, that is the algebra consisting of scalars and bivectors, isisomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
to the quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quatern ...
s, H. This can be seen by comparing the basis to the quaternion basis, or from the above product which is identical to the quaternion product, except for a change of sign which relates to the negative products in the bivector scalar product . Other quaternion properties can be similarly related to or derived from geometric algebra.
This suggests that the usual split of a quaternion into scalar and vector parts would be better represented as a split into scalar and bivector parts; if this is done the quaternion product is merely the geometric product. It also relates quaternions in three dimensions to complex numbers in two, as each is isomorphic to the even subalgebra for the dimension, a relationship that generalises to higher dimensions.
Rotation vector
The rotation vector, from theaxis–angle representation
In mathematics, the axis–angle representation of a rotation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector indicating the direction of an axis of rotation, and an angle describing the magnitu ...
of rotations, is a compact way of representing rotations in three dimensions. In its most compact form, it consists of a vector, the product of a unit vector
In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat").
The term ''direction vecto ...
''ω'' that is the axis of rotation
Rotation around a fixed axis is a special case of rotational motion. The fixed-axis hypothesis excludes the possibility of an axis changing its orientation and cannot describe such phenomena as wobbling or precession. According to Euler's rota ...
with the (signed) angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle.
Angles formed by two ...
of rotation ''θ'', so that the magnitude of the overall rotation vector ''θω'' equals the (unsigned) rotation angle.
The quaternion associated with the rotation is
:
In geometric algebra the rotation is represented by a bivector. This can be seen in its relation to quaternions. Let Ω be a unit bivector in the plane of rotation, and let ''θ'' be the angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, of namely angle, that a figure is rotated about a fixed point, often the center of a circle. A clockwise rotation is considered a negative rotation, so that, for instance, ...
. Then the rotation bivector is Ω''θ''. The quaternion closely corresponds to the exponential of half of the bivector Ω''θ''. That is, the components of the quaternion correspond to the scalar and bivector parts of the following expression:
The exponential can be defined in terms of its power series, and easily evaluated using the fact that Ω squared is −1.
So rotations can be represented by bivectors. Just as quaternions are elements of the geometric algebra, they are related by the exponential map in that algebra.
Rotors
The bivector Ω''θ'' generates a rotation through the exponential map. The even elements generated rotate a general vector in three dimensions in the same way as quaternions: As in two dimensions, the quantity ''e''-Ω''θ''/2 is called arotor
Rotor may refer to:
Science and technology
Engineering
*Rotor (electric), the non-stationary part of an alternator or electric motor, operating with a stationary element so called the stator
* Helicopter rotor, the rotary wing(s) of a rotorcraft ...
and written ''R''. The quantity ''e''Ω''θ''/2 is then ''R''−1, and they generate rotations as This is identical to two dimensions, except here rotors are four-dimensional objects isomorphic to the quaternions. This can be generalised to all dimensions, with rotors, elements of the even subalgebra with unit magnitude, being generated by the exponential map from bivectors. They form a double cover over the rotation group, so the rotors ''R'' and −''R'' represent the same rotation.
Matrices
Axial vectors
axial vector
In physics and mathematics, a pseudovector (or axial vector) is a quantity that is defined as a function of some vectors or other geometric shapes, that resembles a vector, and behaves like a vector in many situations, but is changed into its ...
. Axial vectors, or pseudovectors, are vectors with the special feature that their coordinates undergo a sign change relative to the usual vectors (also called "polar vectors") under inversion through the origin, reflection in a plane, or other orientation-reversing linear transformation. Examples include quantities like torque
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of th ...
, angular momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed syst ...
and vector magnetic field
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to ...
s. Quantities that would use axial vectors in vector algebra In mathematics, vector algebra may mean:
* Linear algebra, specifically the basic algebraic operations of vector addition and scalar multiplication; see vector space.
* The algebraic operations in vector calculus, namely the specific additional stru ...
are properly represented by bivectors in geometric algebra.
More precisely, if an underlying orientation is chosen, the axial vectors are naturally identified with the usual vectors; the Hodge dual
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the al ...
then gives the isomorphism between axial vectors and bivectors, so each axial vector is associated with a bivector and vice versa; that is
:
where ∗ indicates the Hodge dual. Note that if the underlying orientation is reversed by inversion through the origin, both the identification of the axial vectors with the usual vectors and the Hodge dual change sign, but the bivectors don't budge. Alternately, using the unit pseudoscalar in Cl3(R), gives
:
This is easier to use as the product is just the geometric product. But it is antisymmetric because (as in two dimensions) the unit pseudoscalar ''i'' squares to −1, so a negative is needed in one of the products.
This relationship extends to operations like the vector-valued cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is ...
and bivector-valued exterior product, as when written as determinant
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and ...
s they are calculated in the same way:
:
so are related by the Hodge dual:
:
Bivectors have a number of advantages over axial vectors. They better disambiguate axial and polar vectors, that is the quantities represented by them, so it is clearer which operations are allowed and what their results are. For example, the inner product of a polar vector and an axial vector resulting from the cross product in the triple product
In geometry and algebra, the triple product is a product of three 3-dimensional vectors, usually Euclidean vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector- ...
should result in a pseudoscalar
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion while a true scalar does not.
Any scalar product between a pseudovector and an ordinary vector is a pseudoscalar. The ...
, a result which is more obvious if the calculation is framed as the exterior product of a vector and bivector. They generalise to other dimensions; in particular bivectors can be used to describe quantities like torque and angular momentum in two as well as three dimensions. Also, they closely match geometric intuition in a number of ways, as seen in the next section.
Geometric interpretation
planes
Plane(s) most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
Plane or planes may also refer to:
Biology
* Plane (tree) or ''Platanus'', wetland native plant
* ''Planes' ...
, or more precisely as directed plane segments. In three dimensions there are three properties of a bivector that can be interpreted geometrically:
* The arrangement of the plane in space, precisely the attitude
Attitude may refer to:
Philosophy and psychology
* Attitude (psychology), an individual's predisposed state of mind regarding a value
* Metaphysics of presence
* Propositional attitude, a relational mental state connecting a person to a pro ...
of the plane (or alternately the rotation
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional ...
, geometric orientation or gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gradi ...
of the plane), is associated with the ratio of the bivector components. In particular the three basis bivectors, e23, e31 and e12, or scalar multiples of them, are associated with the ''yz''-plane, ''zx''-plane and ''xy''-plane respectively.
* The magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
of the bivector is associated with the area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape
A shape or figure is a graphics, graphical representation of an obje ...
of the plane segment. The area does not have a particular shape so any shape can be used. It can even be represented in other ways, such as by an angular measure. But if the vectors are interpreted as lengths the bivector is usually interpreted as an area with the same units, as follows.
* Like the direction of a vector
Vector most often refers to:
*Euclidean vector, a quantity with a magnitude and a direction
*Vector (epidemiology), an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematic ...
a plane associated with a bivector has a direction, a circulation or a sense of rotation in the plane, which takes two values seen as clockwise and counterclockwise
Two-dimensional rotation can occur in two possible directions. Clockwise motion (abbreviated CW) proceeds in the same direction as a clock's hands: from the top to the right, then down and then to the left, and back up to the top. The opposite ...
when viewed from viewpoint not in the plane. This is associated with a change of sign in the bivector, that is if the direction is reversed the bivector is negated. Alternately if two bivectors have the same attitude and magnitude but opposite directions then one is the negative of the other.
* If imagined as a parallelogram, with the origin for the vectors at 0, then signed area is the determinant
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and ...
of the vectors' Cartesian coordinates ().
parallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equa ...
with edges a and b, as shown in the diagram. One interpretation is that the area is swept out by b as it moves along a. The exterior product is antisymmetric, so reversing the order of a and b to make a move along b results in a bivector with the opposite direction that is the negative of the first. The plane of bivector contains both a and b so they are both parallel to the plane.
Bivectors and axial vectors are related by Hodge dual
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the al ...
. In a real vector space the Hodge dual relates a subspace to its orthogonal complement In the mathematical fields of linear algebra and functional analysis, the orthogonal complement of a subspace ''W'' of a vector space ''V'' equipped with a bilinear form ''B'' is the set ''W''⊥ of all vectors in ''V'' that are orthogonal to every ...
, so if a bivector is represented by a plane then the axial vector associated with it is simply the plane's surface normal
In geometry, a normal is an object such as a line, ray, or vector that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the (infinite) line perpendicular to the tangent line to the curve at ...
. The plane has two normals, one on each side, giving the two possible orientation
Orientation may refer to:
Positioning in physical space
* Map orientation, the relationship between directions on a map and compass directions
* Orientation (housing), the position of a building with respect to the sun, a concept in building de ...
s for the plane and bivector.
 This relates the
This relates the cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is ...
to the exterior product
In mathematics, specifically in topology,
the interior of a subset of a topological space is the union of all subsets of that are open in .
A point that is in the interior of is an interior point of .
The interior of is the complement of the ...
. It can also be used to represent physical quantities, like torque
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of th ...
and angular momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed syst ...
. In vector algebra they are usually represented by vectors, perpendicular to the plane of the force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a p ...
, linear momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and ...
or displacement that they are calculated from. But if a bivector is used instead the plane is the plane of the bivector, so is a more natural way to represent the quantities and the way they act. It also unlike the vector representation generalises into other dimensions.
The product of two bivectors has a geometric interpretation. For non-zero bivectors A and B the product can be split into symmetric and antisymmetric parts as follows:
:
Like vectors these have magnitudes and , where ''θ'' is the angle between the planes. In three dimensions it is the same as the angle between the normal vectors dual to the planes, and it generalises to some extent in higher dimensions.
prism
Prism usually refers to:
* Prism (optics), a transparent optical component with flat surfaces that refract light
* Prism (geometry), a kind of polyhedron
Prism may also refer to:
Science and mathematics
* Prism (geology), a type of sedimentary ...
with a, b, c and as edges. This corresponds to the two ways of calculating the area using the distributivity
In mathematics, the distributive property of binary operations generalizes the distributive law, which asserts that the equality
x \cdot (y + z) = x \cdot y + x \cdot z
is always true in elementary algebra.
For example, in elementary arithmetic, ...
of the exterior product:
:
This only works in three dimensions as it is the only dimension where a vector parallel to both bivectors must exist. In higher dimensions bivectors generally are not associated with a single plane, or if they are (simple bivectors) two bivectors may have no vector in common, and so sum to a non-simple bivector.
Four dimensions
In four dimensions the basis elements for the space ⋀2R4 of bivectors are (e12, e13, e14, e23, e24, e34), so a general bivector is of the form :Orthogonality
In four dimensions the Hodge dual of a bivector is a bivector, and the space ⋀2R4 is dual to itself. Normal vectors are not unique, instead every plane is orthogonal to all the vectors in its Hodge dual space. This can be used to partition the bivectors into two 'halves', in the following way. We have three pairs of orthogonal bivectors: (e12, e34), (e13, e24) and (e14, e23). There are four distinct ways of picking one bivector from each of the first two pairs, and once these first two are picked their sum yields the third bivector from the other pair. For example, (e12, e13, e14) and (e23, e24, e34).Simple bivectors in 4D
In four dimensions bivectors are generated by the exterior product of vectors in R4, but with one important difference from R3 and R2. In four dimensions not all bivectors are simple. There are bivectors such as that cannot be generated by the exterior product of two vectors. This also means they do not have a real, that is scalar, square. In this case : The element e1234 is the pseudoscalar in Cl4, distinct from the scalar, so the square is non-scalar. All bivectors in four dimensions can be generated using at most two exterior products and four vectors. The above bivector can be written as : Similarly, every bivector can be written as the sum of two simple bivectors. It is useful to choose two orthogonal bivectors for this, and this is always possible to do. Moreover, for a generic bivector the choice of simple bivectors is unique, that is, there is only one way to decompose into orthogonal bivectors; the only exception is when the two orthogonal bivectors have equal magnitudes (as in the above example): in this case the decomposition is not unique. The decomposition is always unique in the case of simple bivectors, with the added bonus that one of the orthogonal parts is zero.Rotations in R4
As in three dimensions bivectors in four dimension generate rotations through the exponential map, and all rotations can be generated this way. As in three dimensions if B is a bivector then the rotor ''R'' is ''e''B/2 and rotations are generated in the same way: : The rotations generated are more complex though. They can be categorised as follows:
: ''
The rotations generated are more complex though. They can be categorised as follows:
: ''simple
Simple or SIMPLE may refer to:
*Simplicity, the state or quality of being simple
Arts and entertainment
* ''Simple'' (album), by Andy Yorke, 2008, and its title track
* "Simple" (Florida Georgia Line song), 2018
* "Simple", a song by Johnn ...
'' rotations are those that fix a plane in 4D, and rotate by an angle "about" this plane.
: ''double
A double is a look-alike or doppelgänger; one person or being that resembles another.
Double, The Double or Dubble may also refer to:
Film and television
* Double (filmmaking), someone who substitutes for the credited actor of a character
* Th ...
'' rotations have only one fixed point, the origin, and rotate through two angles about two orthogonal planes. In general the angles are different and the planes are uniquely specified
: ''isoclinic In mathematics, specifically group theory, isoclinism is an equivalence relation on groups which generalizes isomorphism. Isoclinism was introduced by to help classify and understand p-groups, although it is applicable to all groups. Isoclinism al ...
'' rotations are double rotations where the angles of rotation are equal. In this case the planes about which the rotation is taking place are not unique.
These are generated by bivectors in a straightforward way. Simple rotations are generated by simple bivectors, with the fixed plane the dual or orthogonal to the plane of the bivector. The rotation can be said to take place about that plane, in the plane of the bivector. All other bivectors generate double rotations, with the two angles of the rotation equalling the magnitudes of the two simple bivectors the non-simple bivector is composed of. Isoclinic rotations arise when these magnitudes are equal, in which case the decomposition into two simple bivectors is not unique.
Bivectors in general do not commute, but one exception is orthogonal bivectors and exponents of them. So if the bivector , where B1 and B2 are orthogonal simple bivectors, is used to generate a rotation it decomposes into two simple rotations that commute as follows:
:
It is always possible to do this as all bivectors can be expressed as sums of orthogonal bivectors.
Spacetime rotations
Spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differen ...
is a mathematical model for our universe used in special relativity. It consists of three space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. In classical physics, physical space is often conceived in three linear dimensions, although modern physicists usually consider ...
dimensions and one time
Time is the continued sequence of existence and events that occurs in an apparently irreversible succession from the past, through the present, into the future. It is a component quantity of various measurements used to sequence events, to ...
dimension combined into a single four-dimensional space. It is naturally described using geometric algebra and bivectors, with the Euclidean metric
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points.
It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore oc ...
replaced by a Minkowski metric
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of Three-dimensional space, three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two Event (rel ...
. That algebra is identical to that of Euclidean space, except the signature
A signature (; from la, signare, "to sign") is a handwritten (and often stylized) depiction of someone's name, nickname, or even a simple "X" or other mark that a person writes on documents as a proof of identity and intent. The writer of a ...
is changed, so
:
(Note the order and indices above are not universal – here e4 is the time-like dimension). The geometric algebra is Cl3,1(R), and the subspace of bivectors is ⋀2R3,1.
The simple bivectors are of two types. The simple bivectors e23, e31 and e12 have negative squares and span the bivectors of the three-dimensional subspace corresponding to Euclidean space, R3. These bivectors generate ordinary rotations in R3.
The simple bivectors e14, e24 and e34 have positive squares and as planes span a space dimension and the time dimension. These also generate rotations through the exponential map, but instead of trigonometric functions, hyperbolic functions are needed, which generates a rotor as follows:
:
where ''Ω'' is the bivector (e14, etc.), identified via the metric with an antisymmetric linear transformation of R3,1. These are Lorentz boost
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation i ...
s, expressed in a particularly compact way, using the same kind of algebra as in R3 and R4.
In general all spacetime rotations are generated from bivectors through the exponential map, that is, a general rotor generated by bivector A is of the form
:
The set of all rotations in spacetime form the Lorentz group
In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicis ...
, and from them most of the consequences of special relativity can be deduced. More generally this show how transformations in Euclidean space and spacetime can all be described using the same kind of algebra.
Maxwell's equations
(Note: in this section traditional 3-vectors are indicated by lines over the symbols and spacetime vector and bivectors by bold symbols, with the vectors J and A exceptionally in uppercase)Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits.
...
are used in physics to describe the relationship between electric
Electricity is the set of physical phenomena associated with the presence and motion of matter that has a property of electric charge. Electricity is related to magnetism, both being part of the phenomenon of electromagnetism, as described by ...
and magnetic
Magnetism is the class of physical attributes that are mediated by a magnetic field, which refers to the capacity to induce attractive and repulsive phenomena in other entities. Electric currents and the magnetic moments of elementary particle ...
fields. Normally given as four differential equations they have a particularly compact form when the fields are expressed as a spacetime bivector from ⋀2R3,1. If the electric and magnetic fields in R3 are and then the ''electromagnetic bivector'' is
:
where e4 is again the basis vector for the time-like dimension and ''c'' is the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant that is important in many areas of physics. The speed of light is exactly equal to ). According to the special theory of relativity, is the upper limit ...
. The product e123 yields the bivector that is Hodge dual to in three dimensions, as discussed above, while e4 as a product of orthogonal vectors is also bivector-valued. As a whole it is the electromagnetic tensor
In electromagnetism, the electromagnetic tensor or electromagnetic field tensor (sometimes called the field strength tensor, Faraday tensor or Maxwell bivector) is a mathematical object that describes the electromagnetic field in spacetime. Th ...
expressed more compactly as a bivector, and is used as follows. First it is related to the 4-current
In special and general relativity, the four-current (technically the four-current density) is the four-dimensional analogue of the electric current density. Also known as vector current, it is used in the geometric context of ''four-dimensional spa ...
J, a vector quantity given by
:
where is current density
In electromagnetism, current density is the amount of charge per unit time that flows through a unit area of a chosen cross section. The current density vector is defined as a vector whose magnitude is the electric current per cross-sectional ar ...
and ''ρ'' is charge density
In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density (symbolized by the Greek letter ρ) is the quantity of charge per unit volume, measured in the SI system in co ...
. They are related by a differential operator ∂, which is
:
The operator ∇ is a differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation that accepts a function and return ...
in geometric algebra, acting on the space dimensions and given by . When applied to vectors ∇·M is the divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the ...
and ∇∧M is the curl
cURL (pronounced like "curl", UK: , US: ) is a computer software project providing a library (libcurl) and command-line tool (curl) for transferring data using various network protocols. The name stands for "Client URL".
History
cURL was fi ...
but with a bivector rather than vector result, that is dual in three dimensions to the curl. For general quantity M they act as grade lowering and raising differential operators. In particular if M is a scalar then this operator is just the gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gradi ...
, and it can be thought of as a geometric algebraic del
Del, or nabla, is an operator used in mathematics (particularly in vector calculus) as a vector differential operator, usually represented by the nabla symbol ∇. When applied to a function defined on a one-dimensional domain, it denotes th ...
operator.
Together these can be used to give a particularly compact form for Maxwell's equations with sources:
:
This equation, when decomposed according to geometric algebra, using geometric products which have both grade raising and grade lowering effects, is equivalent to Maxwell's four equations. It is also related to the electromagnetic four-potential
An electromagnetic four-potential is a relativistic vector function from which the electromagnetic field can be derived. It combines both an electric scalar potential and a magnetic vector potential into a single four-vector.Gravitation, J.A. Whe ...
, a vector A given by
:
where is the vector magnetic potential and ''V'' is the electric potential. It is related to the electromagnetic bivector as follows
:
using the same differential operator ∂.
Higher dimensions
As has been suggested in earlier sections much of geometric algebra generalises well into higher dimensions. The geometric algebra for the real space R''n'' is Cl''n''(R), and the subspace of bivectors is ⋀2R''n''. The number of simple bivectors needed to form a general bivector rises with the dimension, so for ''n'' odd it is , for ''n'' even it is . So for four andfive
5 is a number, numeral, and glyph.
5, five or number 5 may also refer to:
* AD 5, the fifth year of the AD era
* 5 BC, the fifth year before the AD era
Literature
* ''5'' (visual novel), a 2008 visual novel by Ram
* ''5'' (comics), an awa ...
dimensions only two simple bivectors are needed but three are required for six
6 is a number, numeral, and glyph.
6 or six may also refer to:
* AD 6, the sixth year of the AD era
* 6 BC, the sixth year before the AD era
* The month of June
Science
* Carbon, the element with atomic number 6
* 6 Hebe, an asteroid
People ...
and seven
7 is a number, numeral, and glyph.
7 or seven may also refer to:
* AD 7, the seventh year of the AD era
* 7 BC, the seventh year before the AD era
* The month of
July
Music Artists
* Seven (Swiss singer) (born 1978), a Swiss recording artist ...
dimensions. For example, in six dimensions with standard basis (e1, e2, e3, e4, e5, e6) the bivector
:
is the sum of three simple bivectors but no less. As in four dimensions it is always possible to find orthogonal simple bivectors for this sum.
Rotations in higher dimensions
As in three and four dimensions rotors are generated by the exponential map, so : is the rotor generated by bivector B. Simple rotations, that take place in aplane of rotation
In geometry, a plane of rotation is an abstract object used to describe or visualize rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as t ...
around a fixed blade
A blade is the portion of a tool, weapon, or machine with an edge that is designed to puncture, chop, slice or scrape surfaces or materials. Blades are typically made from materials that are harder than those they are to be used on. Historic ...
of dimension are generated by simple bivectors, while other bivectors generate more complex rotations which can be described in terms of the simple bivectors they are sums of, each related to a plane of rotation. All bivectors can be expressed as the sum of orthogonal and commutative simple bivectors, so rotations can always be decomposed into a set of commutative rotations about the planes associated with these bivectors. The group of the rotors in ''n'' dimensions is the spin group
In mathematics the spin group Spin(''n'') page 15 is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when )
:1 \to \mathrm_2 \to \operatorname(n) \to \operatorname(n) \to 1.
As a L ...
, Spin(''n'').
One notable feature, related to the number of simple bivectors and so rotation planes, is that in odd dimensions every rotation has a fixed axis – it is misleading to call it an axis of rotation as in higher dimensions rotations are taking place in multiple planes orthogonal to it. This is related to bivectors, as bivectors in odd dimensions decompose into the same number of bivectors as the even dimension below, so have the same number of planes, but one extra dimension. As each plane generates rotations in two dimensions in odd dimensions there must be one dimension, that is an axis, that is not being rotated.
Bivectors are also related to the rotation matrix in ''n'' dimensions. As in three dimensions the characteristic equation of the matrix can be solved to find the eigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted b ...
. In odd dimensions this has one real root, with eigenvector the fixed axis, and in even dimensions it has no real roots, so either all or all but one of the roots are complex conjugate pairs. Each pair is associated with a simple component of the bivector associated with the rotation. In particular the log of each pair is ± the magnitude, while eigenvectors generated from the roots are parallel to and so can be used to generate the bivector. In general the eigenvalues and bivectors are unique, and the set of eigenvalues gives the full decomposition into simple bivectors; if roots are repeated then the decomposition of the bivector into simple bivectors is not unique.
Projective geometry
Geometric algebra can be applied toprojective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, pro ...
in a straightforward way. The geometric algebra used is , the algebra of the real vector space R''n''. This is used to describe objects in the real projective space
In mathematics, real projective space, denoted or is the topological space of lines passing through the origin 0 in It is a compact, smooth manifold of dimension , and is a special case of a Grassmannian space.
Basic properties Construction
A ...
RP''n''−1. The non-zero vectors in Cl''n''(R) or R''n'' are associated with points in the projective space so vectors that differ only by a scale factor, so their exterior product is zero, map to the same point. Non-zero simple bivectors in ⋀2R''n'' represent lines in RP''n''−1, with bivectors differing only by a (positive or negative) scale factor representing the same line.
A description of the projective geometry can be constructed in the geometric algebra using basic operations. For example, given two distinct points in RP''n''−1 represented by vectors a and b the line containing them is given by (or ). Two lines intersect in a point if for their bivectors A and B. This point is given by the vector
:
The operation "∨" is the meet, which can be defined as above in terms of the join, for non-zero . Using these operations projective geometry can be formulated in terms of geometric algebra. For example, given a third (non-zero) bivector C the point p lies on the line given by C if and only if
:
So the condition for the lines given by A, B and C to be collinear is
:
which in Cl3(R) and RP2 simplifies to
:
where the angle brackets denote the scalar part of the geometric product. In the same way all projective space operations can be written in terms of geometric algebra, with bivectors representing general lines in projective space, so the whole geometry can be developed using geometric algebra.
Tensors and matrices
As noted above a bivector can be written as a skew-symmetric matrix, which through the exponential map generates a rotation matrix that describes the same rotation as the rotor, also generated by the exponential map but applied to the vector. But it is also used with other bivectors such as theangular velocity tensor
In physics, angular velocity or rotational velocity ( or ), also known as angular frequency vector,(UP1) is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an obje ...
and the electromagnetic tensor
In electromagnetism, the electromagnetic tensor or electromagnetic field tensor (sometimes called the field strength tensor, Faraday tensor or Maxwell bivector) is a mathematical object that describes the electromagnetic field in spacetime. Th ...
, respectively a 3×3 and 4×4 skew-symmetric matrix or tensor.
Real bivectors in ⋀2R''n'' are isomorphic to ''n''×''n'' skew-symmetric matrices, or alternately to antisymmetric tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tenso ...
s of degree 2 on R''n''. While bivectors are isomorphic to vectors (via the dual) in three dimensions they can be represented by skew-symmetric matrices in any dimension. This is useful for relating bivectors to problems described by matrices, so they can be re-cast in terms of bivectors, given a geometric interpretation, then often solved more easily or related geometrically to other bivector problems.
More generally every real geometric algebra is isomorphic to a matrix algebra. These contain bivectors as a subspace, though often in a way which is not especially useful. These matrices are mainly of interest as a way of classifying Clifford algebras.
See also
*Multivector
In multilinear algebra, a multivector, sometimes called Clifford number, is an element of the exterior algebra of a vector space . This algebra is graded, associative and alternating, and consists of linear combinations of simple -vectors (a ...
*Multilinear algebra
Multilinear algebra is a subfield of mathematics that extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of ''p' ...
*Dyadics In mathematics, specifically multilinear algebra, a dyadic or dyadic tensor is a second order tensor, written in a notation that fits in with vector algebra.
There are numerous ways to multiply two Euclidean vectors. The dot product takes in two v ...
Notes
General references
* * * * {{Linear algebra * Geometric algebra Multilinear algebra Vector calculus Tensors