|
Standard Translation
{{short description, Algorithm in modal logic In modal logic, standard translation is a logic translation that transforms formulas of modal logic into formulas of first-order logic which capture the meaning of the modal formulas. Standard translation is defined inductively on the structure of the formula. In short, atomic formulas are mapped onto unary predicates and the objects in the first-order language are the accessible worlds. The logical connectives from propositional logic remain untouched and the modal operators are transformed into first-order formulas according to their semantics. Definition Standard translation is defined as follows: *ST_x(p) \equiv P(x), where p is an atomic formula; P(x) is true when p holds in world x. *ST_x(\top) \equiv \top *ST_x(\bot) \equiv \bot *ST_x(\neg \varphi) \equiv \neg ST_x(\varphi) *ST_x(\varphi \wedge \psi) \equiv ST_x(\varphi) \wedge ST_x(\psi) *ST_x(\varphi \vee \psi) \equiv ST_x(\varphi) \vee ST_x(\psi) *ST_x(\varphi \rightarrow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Logic
Modal logic is a collection of formal systems developed to represent statements about necessity and possibility. It plays a major role in philosophy of language, epistemology, metaphysics, and natural language semantics. Modal logics extend other systems by adding unary operators \Diamond and \Box, representing possibility and necessity respectively. For instance the modal formula \Diamond P can be read as "possibly P" while \Box P can be read as "necessarily P". Modal logics can be used to represent different phenomena depending on what kind of necessity and possibility is under consideration. When \Box is used to represent epistemic necessity, \Box P states that P is epistemically necessary, or in other words that it is known. When \Box is used to represent deontic necessity, \Box P states that P is a moral or legal obligation. In the standard relational semantics for modal logic, formulas are assigned truth values relative to a '' possible world''. A formula's truth value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Variables And Bound Variables
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation (symbol) that specifies places in an expression where substitution may take place and is not a parameter of this or any container expression. Some older books use the terms real variable and apparent variable for free variable and bound variable, respectively. The idea is related to a placeholder (a symbol that will later be replaced by some value), or a wildcard character that stands for an unspecified symbol. In computer programming, the term free variable refers to variables used in a function that are neither local variables nor parameters of that function. The term non-local variable is often a synonym in this context. A bound variable, in contrast, is a variable that has been ''bound'' to a specific value or range of values in the domain of discourse or universe. This may be achieved through the use of logical q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johan Van Benthem (logician)
Johannes Franciscus Abraham Karel (Johan) van Benthem (born 12 June 1949 in Rijswijk) is a University Professor (') of logic at the University of Amsterdam at the Institute for Logic, Language and Computation and professor of philosophy at Stanford University (at CSLI). He was awarded the Spinozapremie in 1996 and elected a Foreign Fellow of the American Academy of Arts & Sciences in 2015. Biography Van Benthem studied physics ( B.Sc. 1969), philosophy ( M.A. 1972) and mathematics ( M.Sc. 1973) at the University of Amsterdam and received a PhD from the same university under supervision of Martin Löb in 1977. Before becoming University Professor in 2003, he held appointments at the University of Amsterdam (1973–1977), at the University of Groningen (1977–1986), and as a professor at the University of Amsterdam (1986–2003). In 1992 he was elected member of the Royal Netherlands Academy of Arts and Sciences. Van Benthem is known for his research in the area of mod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Depth
In modal logic, the modal depth of a formula is the deepest nesting of modal operators (commonly \Box and \Diamond). Modal formulas without modal operators have a modal depth of zero. Definition Modal depth can be defined as follows. Let MD(\phi) be a function that computes the modal depth for a modal formula \phi: :MD(p) = 0, where p is an atomic formula. :MD(\top) = 0 :MD(\bot) = 0 :MD(\neg \varphi) = MD(\varphi) :MD(\varphi \wedge \psi) = max(MD(\varphi), MD(\psi)) :MD(\varphi \vee \psi) = max(MD(\varphi), MD(\psi)) :MD(\varphi \rightarrow \psi) = max(MD(\varphi), MD(\psi)) :MD(\Box \varphi) = 1 + MD(\varphi) :MD(\Diamond \varphi) = 1 + MD(\varphi) Example The following computation gives the modal depth of \Box ( \Box p \rightarrow p ): :MD(\Box ( \Box p \rightarrow p )) = :1 + MD( \Box p \rightarrow p) = :1 + max(MD(\Box p), MD(p)) = :1 + max(1 + MD(p), 0) = :1 + max(1 + 0, 0) = :1 + 1 =:2 Modal depth and semantics The modal depth of a formula indicates 'how far' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antecedent (logic)
An antecedent is the first half of a hypothetical proposition, whenever the if-clause precedes the then-clause. In some contexts the antecedent is called the ''protasis''. Examples: * If P, then Q. This is a nonlogical formulation of a hypothetical proposition. In this case, the antecedent is P, and the consequent is Q. In an implication, if \phi implies \psi then \phi is called the antecedent and \psi is called the consequent.Sets, Functions and Logic - An Introduction to Abstract Mathematics, Keith Devlin, Chapman & Hall/CRC Mathematics, 3rd ed., 2004 Antecedent and consequent are connected via logical connective to form a proposition. * If X is a man, then X is mortal. "X is a man" is the antecedent for this proposition. * If men have walked on the moon, then I am the king of France. Here, "men have walked on the moon" is the antecedent. Let y=x+1. If x=1 then y=2 See also * Consequent * Affirming the consequent (fallacy) * Denying the antecedent (fallacy) * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Implication
Logical consequence (also entailment) is a fundamental concept in logic, which describes the relationship between statements that hold true when one statement logically ''follows from'' one or more statements. A valid logical argument is one in which the conclusion is entailed by the premises, because the conclusion is the consequence of the premises. The philosophical analysis of logical consequence involves the questions: In what sense does a conclusion follow from its premises? and What does it mean for a conclusion to be a consequence of premises?Beall, JC and Restall, Greg, Logical Consequence' The Stanford Encyclopedia of Philosophy (Fall 2009 Edition), Edward N. Zalta (ed.). All of philosophical logic is meant to provide accounts of the nature of logical consequence and the nature of logical truth. Logical consequence is necessary and formal, by way of examples that explain with formal proof and models of interpretation. A sentence is said to be a logical con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vacuous Truth
In mathematics and logic, a vacuous truth is a conditional or universal statement (a universal statement that can be converted to a conditional statement) that is true because the antecedent cannot be satisfied. For example, the statement "she does not own a cell phone" will imply that the statement "all of her cell phones are turned off" will be assigned a truth value. Also, the statement "all of her cell phones are turned ''on''" would also be vacuously true, as would the conjunction of the two: "all of her cell phones are turned on ''and'' turned off", which would otherwise be incoherent and false. For that reason, it is sometimes said that a statement is vacuously true because it is meaningless. More formally, a relatively well-defined usage refers to a conditional statement (or a universal conditional statement) with a false antecedent. One example of such a statement is "if Tokyo is in France, then the Eiffel Tower is in Bolivia". Such statements are considered vacuous t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multimodal Logic
A multimodal logic is a modal logic that has more than one primitive modal operator. They find substantial applications in theoretical computer science. Overview A modal logic with ''n'' primitive unary modal operators \Box_i, i\in \ is called an ''n''-modal logic. Given these operators and negation, one can always add \Diamond_i modal operators defined as \Diamond_i P if and only if \lnot \Box_i \lnot P. Perhaps the first substantive example of a two-modal logic is Arthur Prior's tense logic, with two modalities, F and P, corresponding to "sometime in the future" and "sometime in the past". A logic with infinitely many modalities is dynamic logic, introduced by Vaughan Pratt in 1976 and having a separate modal operator for every regular expression. A version of temporal logic introduced in 1977 and intended for program verification has two modalities, corresponding to dynamic logic's 'A''and 'A''*modalities for a single program ''A'', understood as the whole universe taki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
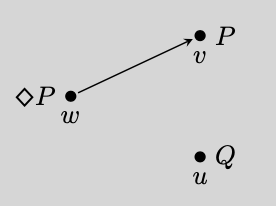
Accessibility Relation
An accessibility relation is a relation which plays a key role in assigning truth values to sentences in the relational semantics for modal logic. In relational semantics, a modal formula's truth value at a ''possible world'' w can depend on what's true at another possible world v, but only if the accessibility relation R relates w to v. For instance, if P holds at some world v such that wRv, the formula \Diamond P will be true at w. The fact wRv is crucial. If R did not relate w to v, then \Diamond P would be false at w unless P also held at some other world u such that wRu. Accessibility relations are motivated conceptually by the fact that natural language modal statements depend on some, but not all alternative scenarios. For instance, the sentence "It might be raining" is not generally judged true simply because one can imagine a scenario where it was raining. Rather, its truth depends on whether such a scenario is ruled out by available information. This fact can be f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kripke Semantics
Kripke semantics (also known as relational semantics or frame semantics, and often confused with possible world semantics) is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke (algebraic semantics existed, but were considered 'syntax in disguise'). Semantics of modal logic The language of propositional modal logic consists of a countably infinite set of propositional variables, a set of truth-functional connectives (in this article \to and \neg), and the modal operator \Box ("necessarily"). The modal operator \Diamond ("possibly") is (classically) the dual of \Box and may be defined in terms of necessity like so: \Di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logic Translation
Logic translation is the process of representing a text in the formal language of a logical system. If the original text is formulated in ordinary language then the term "natural language formalization" is often used. An example is the translation of the English sentence "some men are bald" into first-order logic as \exist x (M(x) \land B(x)). In this regard, the purpose is to reveal the logical structure of arguments. This makes it possible to use the precise rules of formal logic to assess whether these arguments are correct. It can also guide reasoning by arriving at new conclusions. Many of the difficulties associated with the process are caused by vague or ambiguous expressions in natural language. For example, the English word "is" can mean that something exists, that it is Identity (philosophy), identical to something else, or that it has a certain Property (philosophy), property. This contrasts with the precise nature of formal logic, which avoids such ambiguities. Nat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Propositional Logic
Propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions (which can be true or false) and relations between propositions, including the construction of arguments based on them. Compound propositions are formed by connecting propositions by logical connectives. Propositions that contain no logical connectives are called atomic propositions. Unlike first-order logic, propositional logic does not deal with non-logical objects, predicates about them, or quantifiers. However, all the machinery of propositional logic is included in first-order logic and higher-order logics. In this sense, propositional logic is the foundation of first-order logic and higher-order logic. Explanation Logical connectives are found in natural languages. In English for example, some examples are "and" ( conjunction), "or" (disjunction), "not" (negation) and "if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |