|
Modal Depth
In modal logic, the modal depth of a formula is the deepest nesting of modal operators (commonly \Box and \Diamond). Modal formulas without modal operators have a modal depth of zero. Definition Modal depth can be defined as follows. Let MD(\phi) be a Function (mathematics), function that computes the modal depth for a modal formula \phi: :MD(p) = 0, where p is an atomic formula. :MD(\top) = 0 :MD(\bot) = 0 :MD(\neg \varphi) = MD(\varphi) :MD(\varphi \wedge \psi) = max(MD(\varphi), MD(\psi)) :MD(\varphi \vee \psi) = max(MD(\varphi), MD(\psi)) :MD(\varphi \rightarrow \psi) = max(MD(\varphi), MD(\psi)) :MD(\Box \varphi) = 1 + MD(\varphi) :MD(\Diamond \varphi) = 1 + MD(\varphi) Example The following computation gives the modal depth of \Box ( \Box p \rightarrow p ): :MD(\Box ( \Box p \rightarrow p )) = :1 + MD( \Box p \rightarrow p) = :1 + max(MD(\Box p), MD(p)) = :1 + max(1 + MD(p), 0) = :1 + max(1 + 0, 0) = :1 + 1 =:2 Modal depth and semantics The modal depth of a formu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Logic
Modal logic is a collection of formal systems developed to represent statements about necessity and possibility. It plays a major role in philosophy of language, epistemology, metaphysics, and natural language semantics. Modal logics extend other systems by adding unary operators \Diamond and \Box, representing possibility and necessity respectively. For instance the modal formula \Diamond P can be read as "possibly P" while \Box P can be read as "necessarily P". Modal logics can be used to represent different phenomena depending on what kind of necessity and possibility is under consideration. When \Box is used to represent epistemic necessity, \Box P states that P is epistemically necessary, or in other words that it is known. When \Box is used to represent deontic necessity, \Box P states that P is a moral or legal obligation. In the standard relational semantics for modal logic, formulas are assigned truth values relative to a ''possible world''. A formula's truth value at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Operator
A modal connective (or modal operator) is a logical connective for modal logic. It is an operator which forms propositions from propositions. In general, a modal operator has the "formal" property of being non-truth-functional in the following sense: The truth-value of composite formulae sometimes depend on factors other than the actual truth-value of their components. In the case of alethic modal logic, a modal operator can be said to be truth-functional in another sense, namely, that of being sensitive only to the distribution of truth-values across possible worlds, actual or not. Finally, a modal operator is "intuitively" characterized by expressing a modal attitude (such as necessity, possibility, belief, or knowledge) about the proposition to which the operator is applied. See also Garson, James, "Modal Logic", The Stanford Encyclopedia of Philosophy (Summer 2021 Edition), Edward N. Zalta (ed.), URL = Syntax for modal operators The syntax rules for modal operators \Box and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Formula
In mathematical logic, an atomic formula (also known as an atom or a prime formula) is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic. Compound formulas are formed by combining the atomic formulas using the logical connectives. The precise form of atomic formulas depends on the logic under consideration; for propositional logic, for example, a propositional variable is often more briefly referred to as an "atomic formula", but, more precisely, a propositional variable is not an atomic formula but a formal expression that denotes an atomic formula. For predicate logic, the atoms are predicate symbols together with their arguments, each argument being a term. In model theory, atomic formulas are merely strings of symbols with a given signature, which may or may not be satisfiable with respect to a given mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kripke Model
Kripke semantics (also known as relational semantics or frame semantics, and often confused with possible world semantics) is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke and André Joyal. It was first conceived for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The development of Kripke semantics was a breakthrough in the theory of non-classical logics, because the model theory of such logics was almost non-existent before Kripke (algebraic semantics existed, but were considered 'syntax in disguise'). Semantics of modal logic The language of propositional modal logic consists of a countably infinite set of propositional variables, a set of truth-functional connectives (in this article \to and \neg), and the modal operator \Box ("necessarily"). The modal operator \Diamond ("possibly") is (classically) the dual of \Box and may be defined in terms of necessity like so: \Di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Validity (logic)
In logic, specifically in deductive reasoning, an argument is valid if and only if it takes a form that makes it impossible for the premises to be true and the conclusion nevertheless to be false. It is not required for a valid argument to have premises that are actually true, but to have premises that, if they were true, would guarantee the truth of the argument's conclusion. Valid arguments must be clearly expressed by means of sentences called well-formed formulas (also called ''wffs'' or simply ''formulas''). The validity of an argument can be tested, proved or disproved, and depends on its logical form. Arguments In logic, an argument is a set of statements expressing the ''premises'' (whatever consists of empirical evidences and axiomatic truths) and an ''evidence-based conclusion.'' An argument is ''valid'' if and only if it would be contradictory for the conclusion to be false if all of the premises are true. Validity doesn't require the truth of the premises, inst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
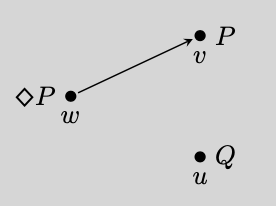
Accessibility Relation
An accessibility relation is a relation which plays a key role in assigning truth values to sentences in the relational semantics for modal logic. In relational semantics, a modal formula's truth value at a ''possible world'' w can depend on what's true at another possible world v, but only if the accessibility relation R relates w to v. For instance, if P holds at some world v such that wRv, the formula \Diamond P will be true at w. The fact wRv is crucial. If R did not relate w to v, then \Diamond P would be false at w unless P also held at some other world u such that wRu. Accessibility relations are motivated conceptually by the fact that natural language modal statements depend on some, but not all alternative scenarios. For instance, the sentence "It might be raining" is not generally judged true simply because one can imagine a scenario where it was raining. Rather, its truth depends on whether such a scenario is ruled out by available information. This fact can be for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Validity (logic)")
