|
Network Controllability
Network controllability concerns the structural controllability of a network. Controllability describes our ability to guide a dynamical system from any initial state to any desired final state in finite time, with a suitable choice of inputs. This definition agrees well with our intuitive notion of control. The controllability of general directed and weighted complex networks has recently been the subject of intense study by a number of groups in wide variety of networks, worldwide. Recent studies by Sharma et al. on multi-type biological networks (gene–gene, miRNA–gene, and protein–protein interaction networks) identified control targets in phenotypically characterized Osteosarcoma showing important role of genes and proteins responsible for maintaining tumor microenvironment. Background Consider the canonical linear time-invariant dynamics on a complex network \dot(t) = \mathbf \cdot \mathbf(t) + \mathbf\cdot \mathbf(t) where the vector \mathbf(t)=(x_1(t),\cdots,x_N(t) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
YYL2
Lynn Lake Airport is an airport located adjacent to Lynn Lake, Manitoba, Canada. It features a paved runway, and is the furthest north runway of its type accessible by highway in Manitoba. After entering into a public/private partnership with YYL Airport Inc. for the continued operation of the airport, long-term operational status is being achieved. See also * List of airports in Manitoba This is a list of airports in Manitoba. It includes all Nav Canada certified and registered water and land airports, Aerodrome#Canada, aerodromes and heliports in the Provinces and territories of Canada, Canadian province of Manitoba. Airport nam ... * Lynn Lake (Eldon Lake) Water Aerodrome References External links * airport website http://www.cyyl.ca/home.html Certified airports in Manitoba {{Manitoba-airport-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Controllability Gramian
In control theory, we may need to find out whether or not a system such as \begin \dot(t) &= \boldsymbol(t) + \boldsymbol(t) \\ \boldsymbol(t) &= \boldsymbol(t) +\boldsymbol(t) \end is controllable, where \boldsymbol, \boldsymbol, \boldsymbol and \boldsymbol are, respectively, n\times n, n\times p, q\times n and q\times p matrices for a system with p inputs, n state variables and q outputs. One of the many ways one can achieve such goal is by the use of the Controllability Gramian. Controllability in LTI Systems Linear Time Invariant (LTI) Systems are those systems in which the parameters \boldsymbol, \boldsymbol, \boldsymbol and \boldsymbol are invariant with respect to time. One can observe if the LTI system is or is not controllable simply by looking at the pair (\boldsymbol,\boldsymbol). Then, we can say that the following statements are equivalent: # The pair (\boldsymbol,\boldsymbol) is controllable. # The n\times n matrix \boldsymbol(t)=\int_^e^\boldsymbole^d\tau=\int_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Minimum Rank Of A Graph
In mathematics, the minimum rank is a graph parameter \operatorname(G) for a graph ''G''. It was motivated by the Colin de Verdière graph invariant. Definition The adjacency matrix of an undirected graph is a symmetric matrix whose rows and columns both correspond to the vertices of the graph. Its elements are all 0 or 1, and the element in row ''i'' and column ''j'' is nonzero whenever vertex ''i'' is adjacent to vertex ''j'' in the graph. More generally, a ''generalized adjacency matrix'' is any symmetric matrix of real numbers with the same pattern of nonzeros off the diagonal (the diagonal elements may be any real numbers). The minimum rank of G is defined as the smallest rank of any generalized adjacency matrix of the graph; it is denoted by \operatorname (G). Properties Here are some elementary properties. *The minimum rank of a graph is always at most equal to ''n'' − 1, where ''n'' is the number of vertices in the graph. *For every induced subgraph ''H'' of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algebraic Graph Theory
Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches. There are three main branches of algebraic graph theory, involving the use of linear algebra, the use of group theory, and the study of graph invariants. Branches of algebraic graph theory Using linear algebra The first branch of algebraic graph theory involves the study of graphs in connection with linear algebra. Especially, it studies the spectrum of the adjacency matrix, or the Laplacian matrix of a graph (this part of algebraic graph theory is also called spectral graph theory). For the Petersen graph, for example, the spectrum of the adjacency matrix is (−2, −2, −2, −2, 1, 1, 1, 1, 1, 3). Several theorems relate properties of the spectrum to other graph properties. As a simple example, a connected graph with diameter ''D'' wil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lenka Zdeborová
Lenka Zdeborová (born 24 November 1980) is a Czech physicist and computer scientist who applies methods from statistical physics to machine learning and constraint satisfaction problems. She is a professor of physics and computer science and communication systems at EPFL (École Polytechnique Fédérale de Lausanne). Life Zdeborová was born in Plzeň and attended a local grammar school where she excelled in math and physics. After living in France with her family and working at the Centre National de la Recherche Scientifique (CNRS), she and her partner moved to Switzerland in 2020. They are currently raising their two children there. Education and career Zdeborová earned a master's degree in physics at Charles University in 2004, and 2008, completed an international dual doctorate ("en cotutelle") at both Charles University and University of Paris-Sud. Her doctoral advisors were Václav Janiš at Charles University, and Marc Mézard at Paris-Sud. After postdoctoral resea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cavity Method
The cavity method is a mathematical method presented by Marc Mézard, Giorgio Parisi and Miguel Angel Virasoro in 1987 to derive and solve some mean field-type models in statistical physics, specially adapted to disordered systems. The method has been used to compute properties of ground states in many condensed matter and optimization problems. Initially invented to deal with the Sherrington–Kirkpatrick model of spin glasses, the cavity method has shown wider applicability. It can be regarded as a generalization of the Bethe– Peierls iterative method in tree-like graphs, to the case of a graph with loops that are not too short. The cavity method can solve many problems also solvable using the replica trick but has the advantage of being more intuitive and less mathematically subtle than replica-based methods. The cavity method proceeds by perturbing a large system with the addition of a non-thermodynamic number of additional constituents and approximating the response of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
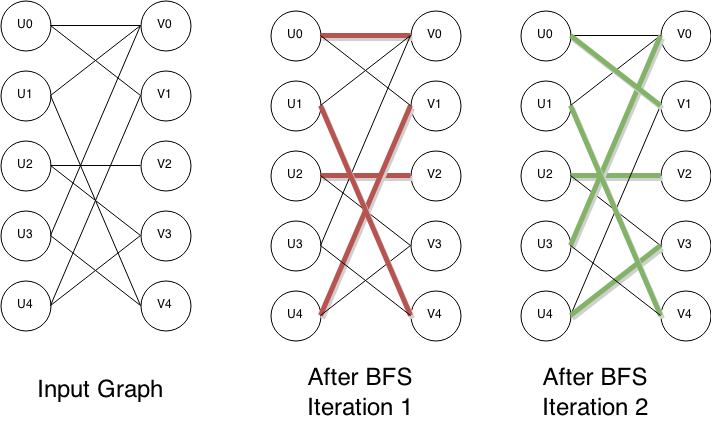
Hopcroft–Karp Algorithm
In computer science, the Hopcroft–Karp algorithm (sometimes more accurately called the Hopcroft–Karp–Karzanov algorithm) is an algorithm that takes a bipartite graph as input and produces a maximum-cardinality matching as output — a set of as many edges as possible with the property that no two edges share an endpoint. It runs in O(, E, \sqrt) time in the worst case, where E is set of edges in the graph, V is set of vertices of the graph, and it is assumed that , E, =\Omega(, V, ). In the case of dense graphs the time bound becomes O(, V, ^), and for sparse random graphs it runs in time O(, E, \log , V, ) with high probability. The algorithm was discovered by and independently by . As in previous methods for matching such as the Hungarian algorithm and the work of , the Hopcroft–Karp algorithm repeatedly increases the size of a partial matching by finding ''augmenting paths''. These paths are sequences of edges of the graph, which alternate between edges in the matchi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Matching (graph Theory)
In the mathematical discipline of graph theory, a matching or independent edge set in an undirected Graph (discrete mathematics), graph is a set of Edge (graph theory), edges without common vertex (graph theory), vertices. In other words, a subset of the edges is a matching if each vertex appears in at most one edge of that matching. Finding a matching in a bipartite graph can be treated as a Flow network, network flow problem. Definitions Given a Graph (discrete mathematics), graph a matching ''M'' in ''G'' is a set of pairwise non-adjacent edges, none of which are loop (graph theory), loops; that is, no two edges share common vertices. A vertex is matched (or saturated) if it is an endpoint of one of the edges in the matching. Otherwise the vertex is unmatched (or unsaturated). A maximal matching is a matching ''M'' of a graph ''G'' that is not a subset of any other matching. A matching ''M'' of a graph ''G'' is maximal if every edge in ''G'' has a non-empty intersectio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Degree (graph Theory)
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for the two ends of the edge. The degree of a vertex v is denoted \deg(v) or \deg v. The maximum degree of a graph G is denoted by \Delta(G), and is the maximum of G's vertices' degrees. The minimum degree of a graph is denoted by \delta(G), and is the minimum of G's vertices' degrees. In the multigraph shown on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, every vertex has the same degree, and so we can speak of ''the'' degree of the graph. A complete graph (denoted K_n, where n is the number of vertices in the graph) is a special kind of regular graph where all vertices have the maximum possible degree, n-1. In a signed graph, the number of positive edges connected to the vertex v is called positive deg(v) and the number of connected negative edges is enti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Controllability
Controllability is an important property of a control system and plays a crucial role in many regulation problems, such as the stabilization of unstable systems using feedback, tracking problems, obtaining optimal control strategies, or, simply prescribing an input that has a desired effect on the state. Controllability and observability are dual notions. Controllability pertains to regulating the state by a choice of a suitable input, while observability pertains to being able to know the state by observing the output (assuming that the input is also being observed). Broadly speaking, the concept of controllability relates to the ability to steer a system around in its configuration space using only certain admissible manipulations. The exact definition varies depending on the framework or the type of models dealt with. The following are examples of variants of notions of controllability that have been introduced in the systems and control literature: * State controllability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Closeness Centrality
In a connected graph, closeness centrality (or closeness) of a node is a measure of centrality in a network, calculated as the reciprocal of the sum of the length of the shortest paths between the node and all other nodes in the graph. Thus, the more central a node is, the ''closer'' it is to all other nodes. Closeness was defined by Bavelas (1950) as the reciprocal of the farness, that is: : C_B(x)= \frac, where d(y,x) is the distance (length of the shortest path) between vertices x and y. This unnormalised version of closeness is sometimes known as status. When speaking of closeness centrality, people usually refer to its normalized form which represents the average length of the shortest paths instead of their sum. It is generally given by the previous formula multiplied by N-1, where N is the number of nodes in the graph resulting in: : C(x)= \frac. The normalization of closeness simplifies the comparison of nodes in graphs of different sizes. For large graphs, the minu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |