Hopcroft–Karp algorithm

In computer science, the Hopcroft–Karp algorithm (sometimes more accurately called the Hopcroft–Karp–Karzanov algorithm) is an algorithm that takes a bipartite graph as input and produces a maximum cardinality matching as output – a set of as many edges as possible with the property that no two edges share an endpoint. It runs in $O(, E, \sqrt)$ time in the worst case, where $E$ is set of edges in the graph, $V$ is set of vertices of the graph, and it is assumed that $, E, =\Omega(, V, )$. In the case of dense graphs the time bound becomes $O(, V, ^)$, and for sparse random graphs it runs in time $O(, E, \log , V, )$ with high probability.

The algorithm was discovered by and independently by . As in previous methods for matching such as the Hungarian algorithm and the work of , the Hopcroft–Karp algorithm repeatedly increases the size of a partial matching by finding ''augmenting paths''. These paths are sequences of edges of the graph, which alternate between edges in the matching and edges out of the partial matching, and where the initial and final edge are not in the partial matching. Finding an augmenting path allows us to increment the size of the partial matching, by simply toggling the edges of the augmenting path (putting in the partial matching those that were not, and vice versa). Simpler algorithms for bipartite matching, such as the Ford–Fulkerson algorithm‚ find one augmenting path per iteration: the Hopcroft-Karp algorithm instead finds a maximal set of shortest augmenting paths, so as to ensure that only $O(\sqrt)$ iterations are needed instead of $O(V)$ iterations. The same performance of $O(, E, \sqrt)$ can be achieved to find maximum cardinality matchings in arbitrary graphs, with the more complicated algorithm of Micali and Vazirani.

The Hopcroft–Karp algorithm can be seen as a special case of Dinic's algorithm for the maximum flow problem.

Augmenting paths

A vertex that is not the endpoint of an edge in some partial matching $M$ is called a ''free vertex''. The basic concept that the algorithm relies on is that of an ''augmenting path'', a path that starts at a free vertex, ends at a free vertex, and alternates between unmatched and matched edges within the path. It follows from this definition that, except for the endpoints, all other vertices (if any) in augmenting path must be non-free vertices. An augmenting path could consist of only two vertices (both free) and single unmatched edge between them.

If $M$ is a matching, and $P$ is an augmenting path relative to $M$, then the symmetric difference of the two sets of edges, $M \oplus P$, would form a matching with size $, M, + 1$. Thus, by finding augmenting paths, an algorithm may increase the size of the matching.

Conversely, suppose that a matching $M$ is not optimal, and let $P$ be the symmetric difference $M \oplus M^*$ where $M^*$ is an optimal matching. Because $M$ and $M^*$ are both matchings, every vertex has degree at most 2 in $P$. So $P$ must form a collection of disjoint cycles, of paths with an equal number of matched and unmatched edges in $M$, of augmenting paths for $M$, and of augmenting paths for $M^*$; but the latter is impossible because $M^*$ is optimal. Now, the cycles and the paths with equal numbers of matched and unmatched vertices do not contribute to the difference in size between $M$ and $M^*$, so this difference is equal to the number of augmenting paths for $M$ in $P$. Thus, whenever there exists a matching $M^*$ larger than the current matching $M$, there must also exist an augmenting path. If no augmenting path can be found, an algorithm may safely terminate, since in this case $M$ must be optimal.

An augmenting path in a matching problem is closely related to the augmenting paths arising in maximum flow problems, paths along which one may increase the amount of flow between the terminals of the flow. It is possible to transform the bipartite matching problem into a maximum flow instance, such that the alternating paths of the matching problem become augmenting paths of the flow problem. It suffices to insert two vertices, source and sink, and insert edges of unit capacity from the source to each vertex in $U$, and from each vertex in $V$ to the sink; and let edges from $U$ to $V$ have unit capacity. A generalization of the technique used in Hopcroft–Karp algorithm to find maximum flow in an arbitrary network is known as Dinic's algorithm.

Algorithm

The algorithm may be expressed in the following pseudocode.

: Input: Bipartite graph $G(U \cup V, E)$
: Output: Matching $M \subseteq E$
: $M \leftarrow \empty$
: repeat
:: $\mathcal P \leftarrow \$ ''maximal set of vertex-disjoint shortest augmenting paths''
:: $M \leftarrow M \oplus (P_1 \cup P_2 \cup \dots \cup P_k)$
: until $\mathcal P = \empty$

In more detail, let $U$ and $V$ be the two sets in the bipartition of $G$, and let the matching from $U$ to $V$ at any time be represented as the set $M$.
The algorithm is run in phases. Each phase consists of the following steps.
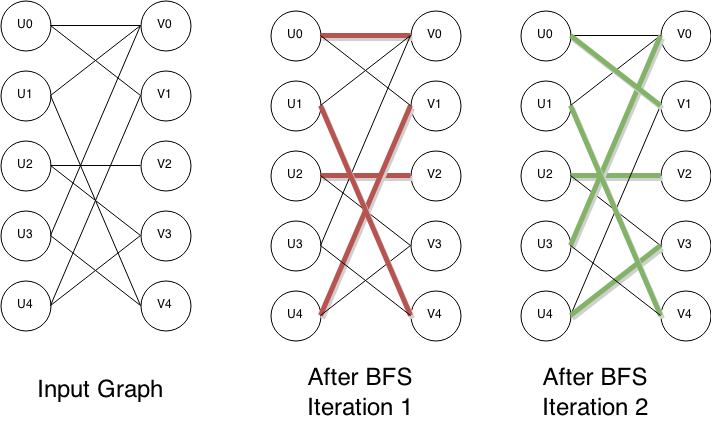
* A breadth-first search partitions the vertices of the graph into layers. The free vertices in $U$ are used as the starting vertices of this search and form the first layer of the partitioning. At the first level of the search, there are only unmatched edges, since the free vertices in $U$ are by definition not adjacent to any matched edges. At subsequent levels of the search, the traversed edges are required to alternate between matched and unmatched. That is, when searching for successors from a vertex in $U$, only unmatched edges may be traversed, while from a vertex in $V$ only matched edges may be traversed. The search terminates at the first layer $k$ where one or more free vertices in $V$ are reached.
* All free vertices in $V$ at layer $k$ are collected into a set $F$. That is, a vertex $v$ is put into $F$ if and only if it ends a shortest augmenting path.
* The algorithm finds a maximal set of ''vertex disjoint'' augmenting paths of length $k$. (''Maximal'' means that no more such paths can be added. This is different from finding the ''maximum'' number of such paths, which would be harder to do. Fortunately, it is sufficient here to find a maximal set of paths.) This set may be computed by depth-first search (DFS) from $F$ to the free vertices in $U$, using the breadth first layering to guide the search: the DFS is only allowed to follow edges that lead to an unused vertex in the previous layer, and paths in the DFS tree must alternate between matched and unmatched edges. Once an augmenting path is found that involves one of the vertices in $F$, the DFS is continued from the next starting vertex. Any vertex encountered during the DFS can immediately be marked as used, since if there is no path from it to $U$ at the current point in the DFS, then that vertex can't be used to reach $U$ at any other point in the DFS. This ensures $O(, E, )$ running time for the DFS. It is also possible to work in the other direction, from free vertices in $U$ to those in $V$, which is the variant used in the pseudocode.
* Every one of the paths found in this way is used to enlarge $M$.

The algorithm terminates when no more augmenting paths are found in the breadth first search part of one of the phases.

Analysis

Each phase consists of a single breadth first search and a single depth-first search. Thus, a single phase may be implemented in $O(, E, )$ time.
Therefore, the first $\sqrt$ phases, in a graph with $, V,$ vertices and $, E,$ edges, take time $O(, E, \sqrt)$.

Each phase increases the length of the shortest augmenting path by at least one: the phase finds a maximal set of augmenting paths of the given length, so any remaining augmenting path must be longer. Therefore, once the initial $\sqrt$ phases of the algorithm are complete, the shortest remaining augmenting path has at least $\sqrt$ edges in it. However, the symmetric difference of the eventual optimal matching and of the partial matching ''M'' found by the initial phases forms a collection of vertex-disjoint augmenting paths and alternating cycles. If each of the paths in this collection has length at least $\sqrt$, there can be at most $\sqrt$ paths in the collection, and the size of the optimal matching can differ from the size of $M$ by at most $\sqrt$ edges. Since each phase of the algorithm increases the size of the matching by at least one, there can be at most $\sqrt$ additional phases before the algorithm terminates.

Since the algorithm performs a total of at most $2\sqrt$ phases, it takes a total time of $O(, E, \sqrt)$ in the worst case.

In many instances, however, the time taken by the algorithm may be even faster than this worst case analysis indicates. For instance, in the average case for sparse bipartite random graphs, (improving a previous result of ) showed that with high probability all non-optimal matchings have augmenting paths of logarithmic length. As a consequence, for these graphs, the Hopcroft–Karp algorithm takes $O(\log , V, )$ phases and $O(, E, \log , V, )$ total time.

Comparison with other bipartite matching algorithms

For sparse graphs, the Hopcroft–Karp algorithm continues to have the best known worst-case performance, but for dense graphs ($, E, =\Omega(, V, ^2)$) a more recent algorithm by achieves a slightly better time bound, $O\left(, V, ^\sqrt\right)$. Their algorithm is based on using a push-relabel maximum flow algorithm and then, when the matching created by this algorithm becomes close to optimum, switching to the Hopcroft–Karp method.

Several authors have performed experimental comparisons of bipartite matching algorithms. Their results in general tend to show that the Hopcroft–Karp method is not as good in practice as it is in theory: it is outperformed both by simpler breadth-first and depth-first strategies for finding augmenting paths, and by push-relabel techniques.

Non-bipartite graphs

The same idea of finding a maximal set of shortest augmenting paths works also for finding maximum cardinality matchings in non-bipartite graphs, and for the same reasons the algorithms based on this idea take $O(\sqrt)$ phases. However, for non-bipartite graphs, the task of finding the augmenting paths within each phase is more difficult. Building on the work of several slower predecessors, showed how to implement a phase in linear time, resulting in a non-bipartite matching algorithm with the same time bound as the Hopcroft–Karp algorithm for bipartite graphs. The Micali–Vazirani technique is complex, and its authors did not provide full proofs of their results; subsequently,
a "clear exposition" was published by and alternative methods were described by other authors. In 2012, Vazirani offered a new simplified proof of the Micali-Vazirani algorithm.

Pseudocode

/*
G = U ∪ V ∪
where U and V are the left and right sides of the bipartite graph and NIL is a special null vertex
*/

function BFS() is
for each u in U do
if Pair_U = NIL then
Dist := 0
Enqueue(Q, u)
else
Dist := ∞
Dist IL:= ∞
while Empty(Q) = false do
u := Dequeue(Q)
if Dist < Dist ILthen
for each v in Adj do
if Dist air_V[v = ∞ then
Dist air_V[v := Dist + 1
Enqueue(Q, Pair_V[v])
return Dist IL≠ ∞

function DFS(u) is
if u ≠ NIL then
for each v in Adj do
if Dist air_V[v_=_Dist_+_1_then
_________________if_DFS(Pair_V[v.html" ;"title=".html" ;"title="air_V[v">air_V[v = Dist + 1 then
if DFS(Pair_V[v">.html" ;"title="air_V[v">air_V[v = Dist + 1 then
if DFS(Pair_V[v = true then
Pair_V := u
Pair_U := v
return true
Dist := ∞
return false
return true

function Hopcroft–Karp is
for each u in U do
Pair_U := NIL
for each v in V do
Pair_V := NIL
matching := 0
while BFS() = true do
for each u in U do
if Pair_U = NIL then
if DFS(u) = true then
matching := matching + 1
return matching

Explanation

Let the vertices of our graph be partitioned in U and V, and consider a partial matching, as indicated by the Pair_U and Pair_V tables that contain the one vertex to which each vertex of U and of V is matched, or NIL for unmatched vertices. The key idea is to add two dummy vertices on each side of the graph: uDummy connected to all unmatched vertices in U and vDummy connected to all unmatched vertices in V. Now, if we run a breadth-first search (BFS) from uDummy to vDummy then we can get the paths of minimal length that connect currently unmatched vertices in U to currently unmatched vertices in V. Note that, as the graph is bipartite, these paths always alternate between vertices in U and vertices in V, and we require in our BFS that when going from V to U, we always select a matched edge. If we reach an unmatched vertex of V, then we end at vDummy and the search for paths in the BFS terminate. To summarize, the BFS starts at unmatched vertices in U, goes to all their neighbors in V, if all are matched then it goes back to the vertices in U to which all these vertices are matched (and which were not visited before), then it goes to all the neighbors of these vertices, etc., until one of the vertices reached in V is unmatched.

Observe in particular that BFS marks the unmatched nodes of U with distance 0, then increments the distance every time it comes back to U. This guarantees that the paths considered in the BFS are of minimal length to connect unmatched vertices of U to unmatched vertices of V while always going back from V to U on edges that are currently part of the matching. In particular, the special NIL vertex, which corresponds to vDummy, then gets assigned a finite distance, so the BFS function returns true iff some path has been found. If no path has been found, then there are no augmenting paths left and the matching is maximal.

If BFS returns true, then we can go ahead and update the pairing for vertices on the minimal-length paths found from U to V: we do so using a depth-first search (DFS). Note that each vertex in V on such a path, except for the last one, is currently matched. So we can explore with the DFS, making sure that the paths that we follow correspond to the distances computed in the BFS. We update along every such path by removing from the matching all edges of the path that are currently in the matching, and adding to the matching all edges of the path that are currently not in the matching: as this is an augmenting path (the first and last edges of the path were not part of the matching, and the path alternated between matched and unmatched edges), then this increases the number of edges in the matching. This is same as replacing the current matching by the symmetric difference between the current matching and the entire path..

Note that the code ensures that all augmenting paths that we consider are vertex disjoint. Indeed, after doing the symmetric difference for a path, none of its vertices could be considered again in the DFS, just because the Dist air_V[v_will_not_be_equal_to_Dist_+_1_(it_would_be_exactly_Dist[u.html" ;"title=".html" ;"title="air_V[v">air_V[v will not be equal to Dist + 1 (it would be exactly Dist[u">.html" ;"title="air_V[v">air_V[v will not be equal to Dist + 1 (it would be exactly Dist[u.

Also observe that the DFS does not visit the same vertex multiple times. This is thanks to the following lines:
Dist = ∞
return false
When we were not able to find any shortest augmenting path from a vertex u, then the DFS marks vertex u by setting Dist to infinity, so that these vertices are not visited again.

One last observation is that we actually don't need uDummy: its role is simply to put all unmatched vertices of U in the queue when we start the BFS. As for vDummy, it is denoted as NIL in the pseudocode above.

See also

* Maximum cardinality matching, the problem solved by the algorithm, and its generalization to non-bipartite graphs
* Assignment problem, a generalization of this problem on weighted graphs, solved e.g. by the Hungarian algorithm
* Edmonds–Karp algorithm for finding maximum flow, a generalization of the Hopcroft–Karp algorithm

Notes

References

*.
*.
*
*
*. As cited by .
*. As cited by .
*.
*.
*
*.
*. Previously announced at the 12th Annual Symposium on Switching and Automata Theory, 1971.
*. Previously announced at the Seminar on Combinatorial Mathematics (Moscow, 1971).
*.
*.
*.
*. As cited by .
*.
*
*.

{{DEFAULTSORT:Hopcroft-Karp algorithm
Graph algorithms
Matching (graph theory)