|
Extension Of A Topological Group
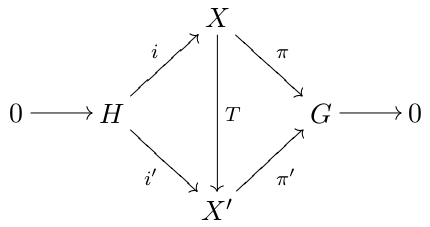
In mathematics, more specifically in topological groups, an extension of topological groups, or a topological extension, is a short exact sequence 0\to H\stackrel X \stackrelG\to 0 where H, X and G are topological groups and i and \pi are continuous homomorphisms which are also open onto their images. Every extension of topological groups is therefore a group extension. Classification of extensions of topological groups We say that the topological extensions :0 \rightarrow H\stackrel X\stackrel G\rightarrow 0 and :0\to H\stackrel X'\stackrel G\rightarrow 0 are equivalent (or congruent) if there exists a topological isomorphism T: X\to X' making commutative the diagram of Figure 1. We say that the topological extension :0 \rightarrow H\stackrel X\stackrel G\rightarrow 0 is a ''split extension'' (or splits) if it is equivalent to the trivial extension :0 \rightarrow H\stackrel H\times G\stackrel G\rightarrow 0 where i_H: H\to H\times G is the natural inclusion over ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Group
In mathematics, topological groups are logically the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures together and consequently they are not independent from each other. Topological groups have been studied extensively in the period of 1925 to 1940. Haar and Weil (respectively in 1933 and 1940) showed that the integrals and Fourier series are special cases of a very wide class of topological groups. Topological groups, along with continuous group actions, are used to study continuous symmetries, which have many applications, for example, in physics. In functional analysis, every topological vector space is an additive topological group with the additional property that scalar multiplication is continuous; consequently, many results from the theory of topological groups can be applied to functional analysis. Formal definition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Short Exact Sequence
An exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next. Definition In the context of group theory, a sequence :G_0\;\xrightarrow\; G_1 \;\xrightarrow\; G_2 \;\xrightarrow\; \cdots \;\xrightarrow\; G_n of groups and group homomorphisms is said to be exact at G_i if \operatorname(f_i)=\ker(f_). The sequence is called exact if it is exact at each G_i for all 1\leq i |
Group Extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the center o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutative Diagram
350px, The commutative diagram used in the proof of the five lemma. In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra. Description A commutative diagram often consists of three parts: * objects (also known as ''vertices'') * morphisms (also known as ''arrows'' or ''edges'') * paths or composites Arrow symbols In algebra texts, the type of morphism can be denoted with different arrow usages: * A monomorphism may be labeled with a \hookrightarrow or a \rightarrowtail. * An epimorphism may be labeled with a \twoheadrightarrow. * An isomorphism may be labeled with a \overset. * The dashed arrow typically represents the claim that the indicated morphism exists (whenever the rest of the diagram holds); the arrow may be optionally labeled as \exist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extensions Groups2
Extension, extend or extended may refer to: Mathematics Logic or set theory * Axiom of extensionality * Extensible cardinal * Extension (model theory) * Extension (predicate logic), the set of tuples of values that satisfy the predicate * Extension (semantics), the set of things to which a property applies * Extension by definitions * Extensional definition, a definition that enumerates every individual a term applies to * Extensionality Other uses * Extension of a polyhedron, in geometry * Exterior algebra, Grassmann's theory of extension, in geometry * Homotopy extension property, in topology * Kolmogorov extension theorem, in probability theory * Linear extension, in order theory * Sheaf extension, in algebraic geometry * Tietze extension theorem, in topology * Whitney extension theorem, in differential geometry * Group extension, in abstract algebra and homological algebra Music * Extension (music), notes that fit outside the standard range * ''Extended'' (Solar Fields al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Sum Of Topological Groups
In mathematics, a topological group G is called the topological direct sum of two subgroups H_1 and H_2 if the map \begin H_1\times H_2 &\longrightarrow G \\ (h_1,h_2) &\longmapsto h_1 h_2 \end is a topological isomorphism, meaning that it is a homeomorphism and a group isomorphism. Definition More generally, G is called the direct sum of a finite set of subgroups H_1, \ldots, H_n of the map \begin \prod^n_ H_i &\longrightarrow G \\ (h_i)_ &\longmapsto h_1 h_2 \cdots h_n \end is a topological isomorphism. If a topological group G is the topological direct sum of the family of subgroups H_1, \ldots, H_n then in particular, as an abstract group (without topology) it is also the direct sum (in the usual way) of the family H_i. Topological direct summands Given a topological group G, we say that a subgroup H is a topological direct summand of G (or that splits topologically from G) if and only if there exist another subgroup K \leq G such that G is the direct su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Numbers
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Compact Group
In mathematics, a locally compact group is a topological group ''G'' for which the underlying topology is locally compact and Hausdorff. Locally compact groups are important because many examples of groups that arise throughout mathematics are locally compact and such groups have a natural measure called the Haar measure. This allows one to define integrals of Borel measurable functions on ''G'' so that standard analysis notions such as the Fourier transform and L^p spaces can be generalized. Many of the results of finite group representation theory are proved by averaging over the group. For compact groups, modifications of these proofs yields similar results by averaging with respect to the normalized Haar integral. In the general locally compact setting, such techniques need not hold. The resulting theory is a central part of harmonic analysis. The representation theory for locally compact abelian groups is described by Pontryagin duality. Examples and counterexamples *Any c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pontryagin Duality
In mathematics, Pontryagin duality is a duality between locally compact abelian groups that allows generalizing Fourier transform to all such groups, which include the circle group (the multiplicative group of complex numbers of modulus one), the finite abelian groups (with the discrete topology), and the additive group of the integers (also with the discrete topology), the real numbers, and every finite dimensional vector space over the reals or a -adic field. The Pontryagin dual of a locally compact abelian group is the locally compact abelian topological group formed by the continuous group homomorphisms from the group to the circle group with the operation of pointwise multiplication and the topology of uniform convergence on compact sets. The Pontryagin duality theorem establishes Pontryagin duality by stating that any locally compact abelian group is naturally isomorphic with its bidual (the dual of its dual). The Fourier inversion theorem is a special case of this th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Groups
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set endowed with a structure, called a ''topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; connectedne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |