mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...

, more specifically in

topological group In mathematics, topological groups are logically the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two str ...

s, an extension of topological groups, or a topological extension, is a

short exact sequence An exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next. Definition In the context o ...

0\to H\stackrel X \stackrelG\to 0

where

H, X

and

G

are topological groups and

i

and

\pi

are continuous homomorphisms which are also open onto their images. Every extension of topological groups is therefore a

group extension In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overs ...

Classification of extensions of topological groups

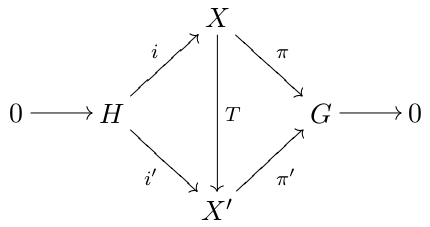
We say that the topological extensions :

0 \rightarrow H\stackrel X\stackrel G\rightarrow 0

and :

0\to H\stackrel X'\stackrel G\rightarrow 0

are equivalent (or congruent) if there exists a topological isomorphism

T: X\to X'

making

commutative In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name o ...

the diagram of Figure 1. Extensions groups2

We say that the topological extension :

0 \rightarrow H\stackrel X\stackrel G\rightarrow 0

is a ''split extension'' (or splits) if it is equivalent to the trivial extension :

0 \rightarrow H\stackrel H\times G\stackrel G\rightarrow 0

where

i_H: H\to H\times G

is the natural inclusion over the first factor and

\pi_G: H\times G\to  G

is the natural projection over the second factor. It is easy to prove that the topological extension

0 \rightarrow H\stackrel X\stackrel G\rightarrow 0

splits if and only if there is a continuous homomorphism

R: X \rightarrow H

such that

R\circ i

is the identity map on

H

Note that the topological extension

0 \rightarrow H\stackrel X\stackrel G\rightarrow 0

splits if and only if the subgroup

i(H)

is a topological direct summand of

X

Examples

* Take

\mathbb R

the

real numbers In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real ...

and

\mathbb Z

the

integer numbers An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language o ...

. Take

\imath

the natural inclusion and

\pi

the natural projection. Then ::

0\to \mathbb Z\stackrel \mathbb R \stackrel\mathbb R/\mathbb Z\to 0

: is an extension of topological abelian groups. Indeed it is an example of a non-splitting extension.

Extensions of locally compact abelian groups (LCA)

An extension of topological abelian groups will be a short exact sequence

0\to H\stackrel X \stackrelG\to 0

where

H, X

and

G

are locally compact abelian groups and

i

and

\pi

are relatively open continuous homomorphisms. *Let be an extension of locally compact abelian groups ::

0\to H\stackrel X \stackrelG\to 0.

: Take

H^\wedge, X^\wedge

and

G^\wedge

the Pontryagin duals of

H, X

and

G

and take

i^\wedge

and

\pi^\wedge

the dual maps of

i

and

\pi

. Then the sequence ::

0\to G^\wedge\stackrel X^\wedge \stackrelH^\wedge\to 0

: is an extension of locally compact abelian groups.

References

{{Reflist Topological groups Topology