|
Direct Sum Of Topological Groups
In mathematics, a topological group G is called the topological direct sum of two subgroups H_1 and H_2 if the map \begin H_1\times H_2 &\longrightarrow G \\ (h_1,h_2) &\longmapsto h_1 h_2 \end is a topological isomorphism, meaning that it is a homeomorphism and a group isomorphism. Definition More generally, G is called the direct sum of a finite set of subgroups H_1, \ldots, H_n of the map \begin \prod^n_ H_i &\longrightarrow G \\ (h_i)_ &\longmapsto h_1 h_2 \cdots h_n \end is a topological isomorphism. If a topological group G is the topological direct sum of the family of subgroups H_1, \ldots, H_n then in particular, as an abstract group (without topology) it is also the Direct sum of groups, direct sum (in the usual way) of the family H_i. Topological direct summands Given a topological group G, we say that a subgroup H is a topological direct summand of G (or that splits topologically from G) if and only if there exist another subgroup K \leq G such that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Group
In mathematics, topological groups are logically the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures together and consequently they are not independent from each other. Topological groups have been studied extensively in the period of 1925 to 1940. Haar and Weil (respectively in 1933 and 1940) showed that the integrals and Fourier series are special cases of a very wide class of topological groups. Topological groups, along with continuous group actions, are used to study continuous symmetries, which have many applications, for example, in physics. In functional analysis, every topological vector space is an additive topological group with the additional property that scalar multiplication is continuous; consequently, many results from the theory of topological groups can be applied to functional analysis. Formal defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgroup
In group theory, a branch of mathematics, given a group ''G'' under a binary operation ∗, a subset ''H'' of ''G'' is called a subgroup of ''G'' if ''H'' also forms a group under the operation ∗. More precisely, ''H'' is a subgroup of ''G'' if the restriction of ∗ to is a group operation on ''H''. This is often denoted , read as "''H'' is a subgroup of ''G''". The trivial subgroup of any group is the subgroup consisting of just the identity element. A proper subgroup of a group ''G'' is a subgroup ''H'' which is a proper subset of ''G'' (that is, ). This is often represented notationally by , read as "''H'' is a proper subgroup of ''G''". Some authors also exclude the trivial group from being proper (that is, ). If ''H'' is a subgroup of ''G'', then ''G'' is sometimes called an overgroup of ''H''. The same definitions apply more generally when ''G'' is an arbitrary semigroup, but this article will only deal with subgroups of groups. Subgroup tests Suppose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homeomorphism
In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same. The word ''homeomorphism'' comes from the Greek words '' ὅμοιος'' (''homoios'') = similar or same and '' μορφή'' (''morphē'') = shape or form, introduced to mathematics by Henri Poincaré in 1895. Very roughly speaking, a topological space is a geometric object, and the homeomorphism is a continuous stretching and bending of the object into a new shape. Thus, a square and a circle are homeomorphic to each other, but a sphere and a torus are not. However, this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic. From the standpoint of group theory, isomorphic groups have the same properties and need not be distinguished. Definition and notation Given two groups (G, *) and (H, \odot), a ''group isomorphism'' from (G, *) to (H, \odot) is a bijective group homomorphism from G to H. Spelled out, this means that a group isomorphism is a bijective function f : G \to H such that for all u and v in G it holds that f(u * v) = f(u) \odot f(v). The two groups (G, *) and (H, \odot) are isomorphic if there exists an isomorphism from one to the other. This is written (G, *) \cong (H, \odot). Often shorter and simpler notations can be used. When the relevant group operations are understood, they are omitted and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direct Sum Of Groups
In mathematics, a group ''G'' is called the direct sumHomology. Saunders MacLane. Springer, Berlin; Academic Press, New York, 1963.László Fuchs. Infinite Abelian Groups of two normal subgroups with trivial intersection if it is generated by the subgroups. In abstract algebra, this method of construction of groups can be generalized to direct sums of vector spaces, modules, and other structures; see the article direct sum of modules for more information. A group which can be expressed as a direct sum of non-trivial subgroups is called ''decomposable'', and if a group cannot be expressed as such a direct sum then it is called ''indecomposable''. Definition A group ''G'' is called the direct sum of two subgroups ''H''1 and ''H''2 if * each ''H''1 and ''H''2 are normal subgroups of ''G'', * the subgroups ''H''1 and ''H''2 have trivial intersection (i.e., having only the identity element e of ''G'' in common), * ''G'' = ⟨''H''1, ''H''2⟩; in other words, ''G'' is generat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
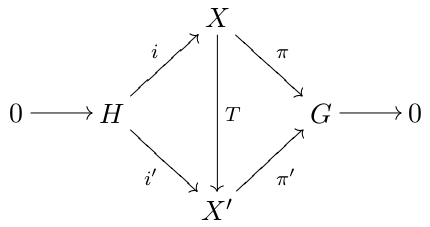
Extension Of A Topological Group
In mathematics, more specifically in topological groups, an extension of topological groups, or a topological extension, is a short exact sequence 0\to H\stackrel X \stackrelG\to 0 where H, X and G are topological groups and i and \pi are continuous homomorphisms which are also open onto their images. Every extension of topological groups is therefore a group extension. Classification of extensions of topological groups We say that the topological extensions :0 \rightarrow H\stackrel X\stackrel G\rightarrow 0 and :0\to H\stackrel X'\stackrel G\rightarrow 0 are equivalent (or congruent) if there exists a topological isomorphism T: X\to X' making commutative the diagram of Figure 1. We say that the topological extension :0 \rightarrow H\stackrel X\stackrel G\rightarrow 0 is a ''split extension'' (or splits) if it is equivalent to the trivial extension :0 \rightarrow H\stackrel H\times G\stackrel G\rightarrow 0 where i_H: H\to H\times G is the natural inclusion ove ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locally Compact Group
In mathematics, a locally compact group is a topological group ''G'' for which the underlying topology is locally compact and Hausdorff. Locally compact groups are important because many examples of groups that arise throughout mathematics are locally compact and such groups have a natural measure called the Haar measure. This allows one to define integrals of Borel measurable functions on ''G'' so that standard analysis notions such as the Fourier transform and L^p spaces can be generalized. Many of the results of finite group representation theory are proved by averaging over the group. For compact groups, modifications of these proofs yields similar results by averaging with respect to the normalized Haar integral. In the general locally compact setting, such techniques need not hold. The resulting theory is a central part of harmonic analysis. The representation theory for locally compact abelian groups is described by Pontryagin duality. Examples and counterexamples *An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as because it is a one-dimensional unit n-sphere, -sphere. If is a point on the unit circle's circumference, then and are the lengths of the legs of a right triangle whose hypotenuse has length 1. Thus, by the Pythagorean theorem, and satisfy the equation x^2 + y^2 = 1. Since for all , and since the reflection of any point on the unit circle about the - or -axis is also on the unit circle, the above equation holds for all points on the unit circle, not only those in the first quadrant. The interior of the unit circle is called the open unit disk, while the interior of the unit circle combined with the unit circle itself is called the closed unit disk. One may also use other notions of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Numbers
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer and the fraction . The rest of the rea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Groups
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set endowed with a structure, called a ''topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |