|
53 Equal Temperament
In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps (equal frequency ratios). Each step represents a frequency ratio of 2, or 22.6415 cents (), an interval sometimes called the Holdrian comma. 53-TET is a tuning of equal temperament in which the tempered perfect fifth is 701.89 cents wide, as shown in Figure 1. The 53-TET tuning equates to the unison, or ''tempers out'', the intervals , known as the schisma, and , known as the kleisma. These are both 5 limit intervals, involving only the primes 2, 3 and 5 in their factorization, and the fact that 53 ET tempers out both characterizes it completely as a 5 limit temperament: it is the only regular temperament tempering out both of these intervals, or commas, a fact which seems to have first been recognized by Japanese music theorist Shohé Tanaka. Because it tempers these out, 53-TET can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
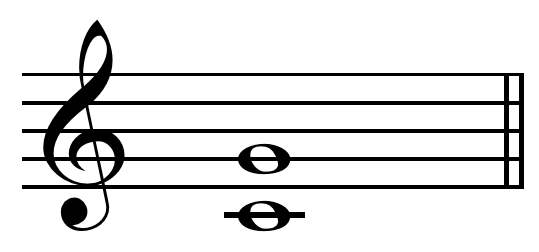
Just Fifth
In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of five consecutive notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant note is a perfect fifth above the tonic note. The perfect fifth is more consonant, or stable, than any other interval except the unison and the octave. It occurs above the root of all major and minor chords (triads) and their extensions. Until the late 19th century, it was often referred to by one of its G ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Holford Macdowall Bosanquet
Robert Holford Macdowall Bosanquet (31 July 1841 – 7 August 1912) was an English scientist and music theorist, and brother of Admiral Sir Day Bosanquet, and philosopher Bernard Bosanquet.Bosanquet was the son of Rev. R. W. Bosanquet of Rock Hall, Alnwick, Northumberland. He was educated at Eton College, and took first class honors in Natural Science and Mathematics at Balliol College, Oxford, and later became a fellow of St. John's College. He was called to the Bar at Lincoln's Inn, London but worked mainly tutoring at Oxford, notably for the Natural Science School, and later was Professor of Acoustics at the Royal College of Music. He was a musician and an authority on organ construction, and published a number of experimental and theoretical papers on acoustics, electromagnetism and astronomy. He was elected Fellow of the Royal Astronomical Society in 1871 and Fellow of the Royal Society in 1890. Bosanquet developed classes for musical tunings used mapping pitches in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term ''limit'' was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name. The harmonic series and the evolution of music Harry Partch, Ivor Darreg, and Ralph David Hill are among the many microtonalists to suggest that music has been slowly evolving to employ higher and higher harmonics in its constructs (see emancipation of the dissonance). In medieval music, only chords made of octaves and perfect fifths (involving relationships among the first three harmonics) were considered consonant. In the West, triadic harmony arose (contenance angloise) around the time of the Renaissance, and triads quickly became the fundamental building blocks of Western music. The major and minor thirds of these triads invoke relationships among the first five harmonic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a "natural philosopher"), widely recognised as one of the greatest mathematicians and physicists and among the most influential scientists of all time. He was a key figure in the philosophical revolution known as the Enlightenment. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for developing infinitesimal calculus. In the , Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. Newton used his mathematical description of gravity to derive Kepler's laws of planetary motion, account for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Just Intonation
In music, just intonation or pure intonation is the tuning of musical intervals Interval may refer to: Mathematics and physics * Interval (mathematics), a range of numbers ** Partially ordered set#Intervals, its generalization from numbers to arbitrary partially ordered sets * A statistical level of measurement * Interval e ... as whole number ratios (such as 3:2 or 4:3) of Frequency, frequencies. An interval (music), interval tuned in this way is said to be pure, and is called a just interval. Just intervals (and chords created by combining them) consist of tones from a single harmonic series (music), harmonic series of an implied fundamental frequency, fundamental. For example, in the diagram, if the notes G3 and C4 (labelled 3 and 4) are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth (music), fourth. In Western musical practice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Five-limit Tuning
Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as . Powers of 2 represent intervallic movements by octaves. Powers of 3 represent movements by intervals of perfect fifths (plus one octave, which can be removed by multiplying by 1/2, i.e., 2−1). Powers of 5 represent intervals of major thirds (plus two octaves, removable by multiplying by 1/4, i.e., 2−2). Thus, 5-limit tunings are constructed entirely from stacking of three basic purely-tuned intervals (octaves, thirds and fifths). Since the perception of consonance seems related to low numbers in the harmonic series, and 5-limit tuning relies on the three lowest primes, 5-limit tuning should be capable of producing very consonan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Just Major Third
Just or JUST may refer to: __NOTOC__ People * Just (surname) * Just (given name) Arts and entertainment * ''Just'', a 1998 album by Dave Lindholm * "Just" (song), a song by Radiohead * "Just", a song from the album ''Lost and Found'' by Mudvayne * ''Just!'' (series), a series of short-story collections for children by Andy Griffiths JUST * Jordan University of Science and Technology, Jordan * Jessore University of Science & Technology, Bangladesh * Jinwen University of Science and Technology, New Taipei, Taiwan Businesses * Just Group plc, a British company specialising in retirement products and services * Just Group, an Australian owner and operator of seven retail brands * JUST, Inc., an American food manufacturing company See also * * List of people known as the Just * Saint-Just (other) * Justice Justice, in its broadest sense, is the principle that people receive that which they deserve, with the interpretation of what then constitutes "deserving" bein ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Holder
William Holder FRS (1616 – 24 January 1698) was an English clergyman and music theorist of the 17th century. His most notable work was his widely known 1694 publication ''A Treatise on the Natural Grounds and Principles of Harmony''. Life He studied at Pembroke Hall, Cambridge, where he became a fellow in 1640. He married Susanna Wren, sister of Christopher Wren, in 1643. In 1662 he received a D.D. Oxon., and was a fellow of the Royal Society in 1663. He became a Canon of St. Paul's in 1672, and served as sub-dean of the Chapel Royal from 1674 until 1689 when he resigned. In 1687 he had been preferred to the rectory of Therfield. A few of his musical compositions survive in the British Library in the Harleian MSS 7338 and 7339. In 1660 at Bletchingdon he taught a deaf mute, Alexander Popham to speak "plainly and distinctly, and with a good and graceful tone". The division of credit for this between Holder and John Wallis became a matter of dispute in the Royal Society.Jonat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. . This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2 (i.e., the untempered perfect fifth), which is ≈702 cents wide. The system dates to Ancient Mesopotamia; see . The system is named, and has been widely misattributed, to Ancient Greeks, notably Pythagoras (sixth century BC) by modern authors of music theory, while Ptolemy, and later Boethius, ascribed the divi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B (), or D and C. It is equal to the frequency ratio = ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often refer to tempering is the Pythagorean comma. The Pythagorean comma can be also defined as the difference between a Pythagorean apotome and a Pythagorean limma (i.e., between a chromatic and a diatonic semitone, as determined in Pythagorean tuning), or the difference between twelve just perfect fifths and seven octaves, or the difference between three Pythagorean ditones and one octave (this is the reason why the Pythagorean comma is also called a ''ditonic comma''). The diminished second, in Pythagorean tuning, is defined as the differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntonic Comma
In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125) (around 21.51 cents). Two notes that differ by this interval would sound different from each other even to untrained ears, , ''BBC''. but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a Didymean comma because it is the amount by which Didymus corrected the |