Just Intonation on:
[Wikipedia]
[Google]
[Amazon]
 In music, just intonation or pure intonation is the tuning of musical intervals as whole number
In music, just intonation or pure intonation is the tuning of musical intervals as whole number


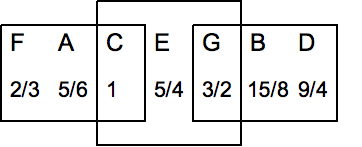 The prominent notes of a given scale may be tuned so that their frequencies form (relatively) small whole number ratios.
The 5-limit diatonic major scale is tuned in such a way that major triads on the tonic, subdominant, and dominant are tuned in the proportion 4:5:6, and minor triads on the mediant and
The prominent notes of a given scale may be tuned so that their frequencies form (relatively) small whole number ratios.
The 5-limit diatonic major scale is tuned in such a way that major triads on the tonic, subdominant, and dominant are tuned in the proportion 4:5:6, and minor triads on the mediant and
 Originally a system of notation to describe scales was devised by Hauptmann and modified by Helmholtz (1877); the starting note is presumed Pythagorean; a “+” is placed between if the next note is a just major third up, a “−” if it is a just minor third, among others; finally, subscript numbers are placed on the second note to indicate how many syntonic commas (81:80) to lower by. Note the use of the “+” between just major thirds, “−” between just minor thirds, “, ” between Pythagorean minor thirds, and “±” between perfect fifths. For example, the Pythagorean major third on C is C+E () while the just major third is C+E1 (). A similar system was devised by Carl Eitz and used in Barbour (1951) in which Pythagorean notes are started with and positive or negative superscript numbers are added indicating how many commas (81:80, syntonic comma) to adjust by. For example, the Pythagorean major third on C is C−E0 while the just major third is C−E−1. An extension of this Pythagorean-based notation to higher primes is the ''Helmholtz / Ellis / Wolf / Monzo system'' of
Originally a system of notation to describe scales was devised by Hauptmann and modified by Helmholtz (1877); the starting note is presumed Pythagorean; a “+” is placed between if the next note is a just major third up, a “−” if it is a just minor third, among others; finally, subscript numbers are placed on the second note to indicate how many syntonic commas (81:80) to lower by. Note the use of the “+” between just major thirds, “−” between just minor thirds, “, ” between Pythagorean minor thirds, and “±” between perfect fifths. For example, the Pythagorean major third on C is C+E () while the just major third is C+E1 (). A similar system was devised by Carl Eitz and used in Barbour (1951) in which Pythagorean notes are started with and positive or negative superscript numbers are added indicating how many commas (81:80, syntonic comma) to adjust by. For example, the Pythagorean major third on C is C−E0 while the just major third is C−E−1. An extension of this Pythagorean-based notation to higher primes is the ''Helmholtz / Ellis / Wolf / Monzo system'' of 
 In 2000–2004, Marc Sabat and
In 2000–2004, Marc Sabat and  Sagittal notation (from Latin ''sagitta'', "arrow") is a system of arrow-like accidentals that indicate prime-number comma alterations to tones in a Pythagorean series. It is used to notate both just intonation and equal temperaments. The size of the symbol indicates the size of the alteration.
The great advantage of such notation systems is that they allow the natural harmonic series to be precisely notated. At the same time, they provide some degree of practicality through their extension of staff notation, as traditionally trained performers may draw on their intuition for roughly estimating pitch height. This may be contrasted with the more abstract use of ratios for representing pitches in which the amount by which two pitches differ and the "direction" of change may not be immediately obvious to most musicians. One caveat is the requirement for performers to learn and internalize a (large) number of new graphical symbols. However, the use of unique symbols reduces harmonic ambiguity and the potential confusion arising from indicating only cent deviations.
Sagittal notation (from Latin ''sagitta'', "arrow") is a system of arrow-like accidentals that indicate prime-number comma alterations to tones in a Pythagorean series. It is used to notate both just intonation and equal temperaments. The size of the symbol indicates the size of the alteration.
The great advantage of such notation systems is that they allow the natural harmonic series to be precisely notated. At the same time, they provide some degree of practicality through their extension of staff notation, as traditionally trained performers may draw on their intuition for roughly estimating pitch height. This may be contrasted with the more abstract use of ratios for representing pitches in which the amount by which two pitches differ and the "direction" of change may not be immediately obvious to most musicians. One caveat is the requirement for performers to learn and internalize a (large) number of new graphical symbols. However, the use of unique symbols reduces harmonic ambiguity and the potential confusion arising from indicating only cent deviations.
Art of the States: microtonal/just intonation
works using just intonation by American composers
Just Intonation
b
Mark Nowitzky
Just intonation
compared with meantone and 12-equal temperaments; a video featuring Pachelbel's canon.
Just Intonation Explained
by Kyle Gann
A selection of Just Intonation works edited by the Just Intonation Network
web published on the Tellus Audio Cassette Magazine project archive at UbuWeb
Medieval Music and Arts Foundation
* Barbieri, Patrizio
(2008) Latina, Il Levante
22 Note Just Intonation Keyboard Software with 12 Indian Instrument Sounds
Libreria Editrice
Plainsound Music Edition
– JI music and research, information about the Helmholtz-Ellis JI Pitch Notation {{Authority control *
 In music, just intonation or pure intonation is the tuning of musical intervals as whole number
In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
s (such as 3:2 or 4:3) of frequencies
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from '' angular frequency''. Frequency is measured in hertz (Hz) which is e ...
. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals (and chords created by combining them) consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 (labelled 3 and 4) are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth.
In Western musical practice, instruments are rarely tuned using only pure intervals—the desire for different keys to have identical intervals in Western music makes this impractical. Some instruments of fixed pitch, such as electric pianos, are commonly tuned using equal temperament
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, ...
, in which all intervals other than octaves consist of irrational-number frequency ratios. Acoustic pianos are usually tuned with the octaves slightly widened, and thus with no pure intervals at all.
Terminology
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: M ...
, or 3-limit tuning, allows ratios including the numbers 2 and 3 and their powers, such as 3:2, a perfect fifth
In music theory, a perfect fifth is the musical interval corresponding to a pair of pitches with a frequency ratio of 3:2, or very nearly so.
In classical music from Western culture, a fifth is the interval from the first to the last of five ...
, and 9:4, a major ninth. Although the interval from C to G is called a perfect fifth for purposes of music analysis regardless of its tuning method, for purposes of discussing tuning systems musicologists may distinguish between a ''perfect fifth'' created using the 3:2 ratio and a ''tempered fifth'' using some other system, such as meantone or equal temperament
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, ...
.
5-limit tuning encompasses ratios additionally using the number 5 and its powers, such as 5:4, a major third
In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and P ...
, and 15:8, a major seventh. The specialized term ''perfect third'' is occasionally used to distinguish the 5:4 ratio from major thirds created using other tuning methods. 7-limit and higher systems use higher partials in the overtone series.
Commas
The comma is a punctuation mark that appears in several variants in different languages. It has the same shape as an apostrophe or single closing quotation mark () in many typefaces, but it differs from them in being placed on the baseline o ...
are very small intervals that result from minute differences between pairs of just intervals. For example, the 5:4 ratio is different from the Pythagorean (3-limit) major third (81:64) by a difference of 81:80, called the syntonic comma.
A Cent is a measure of interval size. It is logarithmic in the musical frequency ratios. The octave is divided into 1200 steps, 100 cents for each semitone.
History
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: M ...
has been attributed to both Pythagoras
Pythagoras of Samos ( grc, Πυθαγόρας ὁ Σάμιος, Pythagóras ho Sámios, Pythagoras the Samian, or simply ; in Ionian Greek; ) was an ancient Ionian Greek philosopher and the eponymous founder of Pythagoreanism. His politic ...
and Eratosthenes
Eratosthenes of Cyrene (; grc-gre, Ἐρατοσθένης ; – ) was a Greek polymath: a mathematician, geographer, poet, astronomer, and music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexand ...
by later writers, but may have been analyzed by other early Greeks or other early cultures as well. The oldest known description of the Pythagorean tuning system appears in Babylonian artifacts.
During the second century AD, Claudius Ptolemy described a 5-limit diatonic scale in his influential text on music theory ''Harmonics'', which he called "intense diatonic". Given ratios of string lengths 120, , 100, 90, 80, 75, , and 60, Ptolemy quantified the tuning of what would later be called the Phrygian scale (equivalent to the major scale
The major scale (or Ionian mode) is one of the most commonly used musical scales, especially in Western music. It is one of the diatonic scales. Like many musical scales, it is made up of seven notes: the eighth duplicates the first at doub ...
beginning and ending on the third note) – 16:15, 9:8, 10:9, 9:8, 16:15, 9:8, and 10:9.
Non-Western music, particularly that built on pentatonic scales, is largely tuned using just intonation. In China, the guqin
The ''guqin'' (; ) is a plucked seven-string Chinese musical instrument. It has been played since ancient times, and has traditionally been favoured by scholars and literati as an instrument of great subtlety and refinement, as highlighted b ...
has a musical scale based on harmonic overtone positions. The dots on its soundboard indicate the harmonic positions: , , , , , , , , , , , , . Indian music has an extensive theoretical framework
A theory is a rational type of abstract thinking about a phenomenon, or the results of such thinking. The process of contemplative and rational thinking is often associated with such processes as observational study or research. Theories may be s ...
for tuning in just intonation.
Diatonic scale

 The prominent notes of a given scale may be tuned so that their frequencies form (relatively) small whole number ratios.
The 5-limit diatonic major scale is tuned in such a way that major triads on the tonic, subdominant, and dominant are tuned in the proportion 4:5:6, and minor triads on the mediant and
The prominent notes of a given scale may be tuned so that their frequencies form (relatively) small whole number ratios.
The 5-limit diatonic major scale is tuned in such a way that major triads on the tonic, subdominant, and dominant are tuned in the proportion 4:5:6, and minor triads on the mediant and submediant
In music, the submediant is the sixth degree () of a diatonic scale. The submediant ("lower mediant") is named thus because it is halfway between tonic and subdominant ("lower dominant") or because its position below the tonic is symmetrical to ...
are tuned in the proportion 10:12:15. Because of the two sizes of wholetone – 9:8 (major wholetone) and 10:9 (minor wholetone) – the supertonic must be microtonally lowered by a syntonic comma to form a pure minor triad.
The 5-limit diatonic major scale ( Ptolemy's intense diatonic scale) on C is shown in the table below:
In this example the interval from D up to A would be a wolf fifth with the ratio , about 680 cents, noticeably smaller than the 702 cents of the pure ratio.
For a justly tuned diatonic minor scale, the mediant is tuned 6:5 and the submediant is tuned 8:5. It would include a tuning of 9:5 for the subtonic. For example on A:
Twelve-tone scale
There are several ways to create a just tuning of the twelve-tone scale.Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: M ...
can produce a twelve-tone scale, but it does so by involving ratios of very large numbers, corresponding to natural harmonics very high in the harmonic series that do not occur widely in physical phenomena. This tuning uses ratios involving only powers of 3 and 2, creating a sequence of just fifths or fourths, as follows:
The ratios are computed with respect to C (the ''base note''). Starting from C, they are obtained by moving six steps (around the circle of fifths
In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths. (This is strictly true in the standard 12-tone equal temperament system — using a different system requires one interval of ...
) to the left and six to the right. Each step consists of a multiplication of the previous pitch by (descending fifth), (ascending fifth), or their inversions ( or ).
Between the enharmonic notes at both ends of this sequence is a pitch ratio of , or about 23 cents, known as the Pythagorean comma. To produce a twelve-tone scale, one of them is arbitrarily discarded. The twelve remaining notes are repeated by increasing or decreasing their frequencies by a power of 2 (the size of one or more octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
s) to build scales with multiple octaves (such as the keyboard of a piano). A drawback of Pythagorean tuning is that one of the twelve fifths in this scale is badly tuned and hence unusable (the wolf fifth, either F–D if G is discarded, or B–G if F is discarded). This twelve-tone scale is fairly close to equal temperament
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, ...
, but it does not offer much advantage for tonal harmony because only the perfect intervals (fourth, fifth, and octave) are simple enough to sound pure. Major thirds, for instance, receive the rather unstable interval of 81:64, sharp of the preferred 5:4 by an 81:80 ratio. The primary reason for its use is that it is extremely easy to tune, as its building block, the perfect fifth, is the simplest and consequently the most consonant
In articulatory phonetics, a consonant is a speech sound that is articulated with complete or partial closure of the vocal tract. Examples are and pronounced with the lips; and pronounced with the front of the tongue; and pronounced ...
interval after the octave and unison.
Pythagorean tuning may be regarded as a "three-limit" tuning system, because the ratios can be expressed as a product of integer powers of only whole numbers less than or equal to 3.
Five-limit tuning
A twelve-tone scale can also be created by compounding harmonics up to the fifth: namely, by multiplying the frequency of a given reference note (the base note) by powers of 2, 3, or 5, or a combination of them. This method is called five-limit tuning. To build such a twelve-tone scale (using C as the base note), we may start by constructing a table containing fifteen pitches: The factors listed in the first row and column are powers of 3 and 5, respectively (e.g., = 3). Colors indicate couples of enharmonic notes with almost identical pitch. The ratios are all expressed relative to C in the centre of this diagram (the base note for this scale). They are computed in two steps: # For each cell of the table, a ''base ratio'' is obtained by multiplying the corresponding factors. For instance, the base ratio for the lower-left cell is # The base ratio is then multiplied by a negative or positive power of 2, as large as needed to bring it within the range of the octave starting from C (from 1:1 to 2:1). For instance, the base ratio for the lower left cell () is multiplied by 2, and the resulting ratio is 64:45, which is a number between 1:1 and 2:1. Note that the powers of 2 used in the second step may be interpreted as ascending or descendingoctave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
s. For instance, multiplying the frequency of a note by 2 means increasing it by 6 octaves. Moreover, each row of the table may be considered to be a sequence of fifths (ascending to the right), and each column a sequence of major thirds (ascending upward). For instance, in the first row of the table, there is an ascending fifth from D and A, and another one (followed by a descending octave) from A to E. This suggests an alternative but equivalent method for computing the same ratios. For instance, one can obtain A, starting from C, by moving one cell to the left and one upward in the table, which means descending by a fifth and ascending by a major third:
Since this is below C, one needs to move up by an octave to end up within the desired range of ratios (from 1:1 to 2:1):
A 12-tone scale is obtained by removing one note for each couple of enharmonic notes. This can be done in at least three ways, which have in common the removal of G, according to a convention which was valid even for C-based Pythagorean and quarter-comma meantone scales. Note that it is a diminished fifth, close to half an octave, above the tonic C, which is a disharmonic interval; also its ratio has the largest values in its numerator and denominator of all tones in the scale, which make it least harmonious: all reasons to avoid it.
This is only one possible strategy of five-limit tuning. It consists of discarding the first column of the table (labeled ""). The resulting 12-tone scale is shown below:
Extension of the twelve-tone scale
The table above uses only low powers of 3 and 5 to build the base ratios. However, it can be easily extended by using higher positive and negative powers of the same numbers, such as 5 = 25, 5 = , 3 = 27, or 3 = . A scale with 25, 35 or even more pitches can be obtained by combining these base ratios.Indian scales
In Indian music, the just diatonic scale described above is used, though there are different possibilities, for instance for the sixth pitch (''Dha''), and further modifications may be made to all pitches excepting ''Sa'' and ''Pa''. Some accounts of Indian intonation system cite a given 22 Shrutis. According to some musicians, one has a scale of a given 12 pitches and ten in addition (the tonic, Shadja (''Sa''), and the pure fifth, Pancham (''Pa''), are inviolate): Where we have ''two'' ratios for a given letter name, we have a difference of 81:80 (or 22 cents), which is known as the syntonic comma. One can see the symmetry, looking at it from the tonic, then the octave. (This is just one example of explaining a 22-Śruti scale of tones. There are many different explanations.)Practical difficulties
Some fixed just intonation scales and systems, such as the diatonic scale above, produce wolf intervals when the approximately equivalent flat note is substituted for a sharp note not available in the scale, or vice versa. The above scale allows a minor tone to occur next to a semitone which produces the awkward ratio 32:27 for D–F, and still worse, a minor tone next to a fourth giving 40:27 for D–A. Moving D down to 10:9 alleviates these difficulties but creates new ones: D–G becomes 27:20, and D–B becomes 27:16. This fundamental problem arises in any system of tuning using a limited number of notes. One can have morefret
A fret is any of the thin strips of material, usually metal wire, inserted laterally at specific positions along the neck or fretboard of a stringed instrument. Frets usually extend across the full width of the neck. On some historical instru ...
s on a guitar
The guitar is a fretted musical instrument that typically has six strings. It is usually held flat against the player's body and played by strumming or plucking the strings with the dominant hand, while simultaneously pressing selected string ...
(or keys on a piano) to handle both As, 9:8 with respect to G and 10:9 with respect to G so that A-C can be played as 6:5 while A-D can still be played as 3:2. 9:8 and 10:9 are less than of an octave apart, so mechanical and performance considerations have made this approach extremely rare. And the problem of how to tune complex chords such as C6add9 (C-E-G-A-D), in typical 5-limit just intonation, is left unresolved (for instance, A could be 4:3 below D (making it 9:8, if G is 1) or 4:3 above E (making it 10:9, if G is 1) but not both at the same time, so one of the fourths in the chord will have to be an out-of-tune wolf interval). Most complex (added-tone and extended) chords usually require intervals beyond common 5-limit ratios in order to sound harmonious (for instance, the previous chord could be tuned to 8:10:12:13:18, using the A note from the 13th harmonic), which implies even more keys or frets. However the frets may be removed entirely—this, unfortunately, makes in-tune fingering of many chords exceedingly difficult, due to the construction and mechanics of the human hand—and the tuning of most complex chords in just intonation is generally ambiguous.
Some composers deliberately use these wolf intervals and other dissonant intervals as a way to expand the tone color palette of a piece of music. For example, the extended piano pieces '' The Well-Tuned Piano'' by LaMonte Young and ''The Harp Of New Albion'' by Terry Riley use a combination of very consonant and dissonant intervals for musical effect. In "Revelation", Michael Harrison goes even further, and uses the tempo of beat patterns produced by some dissonant intervals as an integral part of several movements.
For many fixed-pitch instruments tuned in just intonation, one cannot change keys without retuning the instrument. For instance, if a piano is tuned in just intonation intervals and a minimum of wolf intervals for the key of G, then only one other key (typically E-flat) can have the same intervals, and many of the keys have a very dissonant and unpleasant sound. This makes modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the '' carrier signal'', with a separate signal called the ''modulation signal'' that typically contains informat ...
within a piece, or playing a repertoire of pieces in different keys, impractical to impossible.
Synthesizer
A synthesizer (also spelled synthesiser) is an electronic musical instrument that generates audio signals. Synthesizers typically create sounds by generating waveforms through methods including subtractive synthesis, additive synthesis ...
s have proven a valuable tool for composers wanting to experiment with just intonation. They can be easily retuned with a microtuner
A microtuner or microtonal tuner is an electronic device or software program designed to modify and test the tuning of musical instruments (in particular synthesizers) with microtonal precision, allowing for the design and construction of microton ...
. Many commercial synthesizers provide the ability to use built-in just intonation scales or to create them manually. Wendy Carlos
Wendy Carlos (born Walter Carlos, November 14, 1939) is an American musician and composer best known for her electronic music and film scores. Born and raised in Rhode Island, Carlos studied physics and music at Brown University before movin ...
used a system on her 1986 album '' Beauty in the Beast'', where one electronic keyboard was used to play the notes, and another used to instantly set the root note to which all intervals were tuned, which allowed for modulation. On her 1987 lecture album ''Secrets of Synthesis'' there are audible examples of the difference in sound between equal temperament and just intonation.
Singing and scale-free instruments
The human voice is among the most pitch-flexible instruments in common use. Pitch can be varied with no restraints and adjusted in the midst of performance, without needing to retune. Although the explicit use of just intonation fell out of favour concurrently with the increasing use of instrumental accompaniment (with its attendant constraints on pitch), most a cappella ensembles naturally tend toward just intonation because of the comfort of its stability. Barbershop quartets are a good example of this. The unfretted stringed instruments such as those from the violin family (the violin, the viola, and the cello), and the double bass are quite flexible in the way pitches can be adjusted. Stringed instruments that are not playing with fixed pitch instruments tend to adjust the pitch of key notes such as thirds and leading tones so that the pitches differ from equal temperament. Trombones have a slide that allows arbitrary tuning during performance. French horns can be tuned by shortening or lengthening the main tuning slide on the back of the instrument, with each individual rotary or piston slide for each rotary or piston valve, and by using the right hand inside the bell to adjust the pitch by pushing the hand in deeper to sharpen the note, or pulling it out to flatten the note while playing. Some natural horns also may adjust the tuning with the hand in the bell, and valved cornets, trumpets, Flugelhorns, Saxhorns, Wagner tubas, and tubas have overall and valve-by-valve tuning slides, like valved horns. Wind instruments with valves are biased towards natural tuning and must be micro-tuned if equal temperament is required. Other wind instruments, although built to a certain scale, can be micro-tuned to a certain extent by using theembouchure
Embouchure () or lipping is the use of the lips, facial muscles, tongue, and teeth in playing a wind instrument. This includes shaping the lips to the mouthpiece of a woodwind instrument or the mouthpiece of a brass instrument. The word is of Fr ...
or adjustments to fingering.
Western composers
Composers often impose alimit
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2019 ...
on how complex the ratios may become. For example, a composer who chooses to write in 7-limit just intonation will not employ ratios that use powers of prime numbers larger than 7. Under this scheme, ratios like 11:7 and 13:6 would not be permitted, because 11 and 13 cannot be expressed as powers of those prime numbers ≤ 7 (''i.e.'' 2, 3, 5, and 7).
Staff notation
 Originally a system of notation to describe scales was devised by Hauptmann and modified by Helmholtz (1877); the starting note is presumed Pythagorean; a “+” is placed between if the next note is a just major third up, a “−” if it is a just minor third, among others; finally, subscript numbers are placed on the second note to indicate how many syntonic commas (81:80) to lower by. Note the use of the “+” between just major thirds, “−” between just minor thirds, “, ” between Pythagorean minor thirds, and “±” between perfect fifths. For example, the Pythagorean major third on C is C+E () while the just major third is C+E1 (). A similar system was devised by Carl Eitz and used in Barbour (1951) in which Pythagorean notes are started with and positive or negative superscript numbers are added indicating how many commas (81:80, syntonic comma) to adjust by. For example, the Pythagorean major third on C is C−E0 while the just major third is C−E−1. An extension of this Pythagorean-based notation to higher primes is the ''Helmholtz / Ellis / Wolf / Monzo system'' of
Originally a system of notation to describe scales was devised by Hauptmann and modified by Helmholtz (1877); the starting note is presumed Pythagorean; a “+” is placed between if the next note is a just major third up, a “−” if it is a just minor third, among others; finally, subscript numbers are placed on the second note to indicate how many syntonic commas (81:80) to lower by. Note the use of the “+” between just major thirds, “−” between just minor thirds, “, ” between Pythagorean minor thirds, and “±” between perfect fifths. For example, the Pythagorean major third on C is C+E () while the just major third is C+E1 (). A similar system was devised by Carl Eitz and used in Barbour (1951) in which Pythagorean notes are started with and positive or negative superscript numbers are added indicating how many commas (81:80, syntonic comma) to adjust by. For example, the Pythagorean major third on C is C−E0 while the just major third is C−E−1. An extension of this Pythagorean-based notation to higher primes is the ''Helmholtz / Ellis / Wolf / Monzo system'' of ASCII
ASCII ( ), abbreviated from American Standard Code for Information Interchange, is a character encoding standard for electronic communication. ASCII codes represent text in computers, telecommunications equipment, and other devices. Because ...
symbols and prime-factor-power vectors described in Monzo's ''Tonalsoft Encyclopaedia''.
While these systems allow precise indication of intervals and pitches in print, more recently some composers have been developing notation methods for Just Intonation using the conventional five-line staff. James Tenney, amongst others, preferred to combine JI ratios with cents deviations from the equal tempered
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, w ...
pitches, indicated in a legend or directly in the score, allowing performers to readily use electronic tuning devices if desired.
Beginning in the 1960s, Ben Johnston had proposed an alternative approach, redefining the understanding of conventional symbols (the seven "white" notes, the sharps and flats) and adding further accidentals, each designed to extend the notation into higher prime limits. His notation "begins with the 16th-century Italian definitions of intervals and continues from there." Johnston notation is based on a diatonic C Major scale tuned in JI (Fig. 4), in which the interval between D (9:8 above C) and A (5:3 above C) is one syntonic comma less than a Pythagorean perfect fifth 3:2. To write a perfect fifth, Johnston introduces a pair of symbols, + and − again, to represent this comma. Thus, a series of perfect fifths beginning with F would proceed C G D A+ E+ B+. The three conventional white notes A E B are tuned as Ptolemaic major thirds (5:4) above F C G respectively. Johnston introduces new symbols for the septimal ( & ), undecimal ( & ), tridecimal ( & ), and further prime-number extensions to create an accidental based exact JI notation for what he has named "Extended Just Intonation" ( Fig. 2 & Fig. 3). For example, the Pythagorean major third on C is C-E+ while the just major third is C-E (Fig. 4).

 In 2000–2004, Marc Sabat and
In 2000–2004, Marc Sabat and Wolfgang von Schweinitz
Wolfgang von Schweinitz (born 7 February 1953 in Hamburg) is a German composer of classical music and an academic teacher.
Career
Schweinitz studied composition at the Hochschule für Musik und Theater Hamburg, from 1971 to 1973 with Gernot Kl ...
worked in Berlin to develop a different accidental-based method, the Extended Helmholtz-Ellis JI Pitch Notation. Following the method of notation suggested by Helmholtz in his classic ''On the Sensations of Tone as a Physiological Basis for the Theory of Music
''On the Sensations of Tone as a Physiological Basis for the Theory of Music'' (German ), commonly referred to as ''Sensations of Tone'', is a foundational work on music acoustics and the perception of sound by Hermann von Helmholtz.
The first G ...
'', incorporating Ellis' invention of cents, and continuing Johnston's step into "Extended JI", Sabat and Schweinitz propose unique symbols (accidentals) for each prime dimension of harmonic space. In particular, the conventional flats, naturals and sharps define a Pythagorean series of perfect fifths. The Pythagorean pitches are then paired with new symbols that commatically alter them to represent various other partials of the harmonic series (Fig. 1). To facilitate quick estimation of pitches, cents indications may be added (e.g. downward deviations below and upward deviations above the respective accidental). A typically used convention is that cent deviations refer to the ''tempered pitch'' implied by the flat, natural, or sharp. A complete legend and fonts for the notation (see samples) are open source and available from the Plainsound Music Edition website. For example, the Pythagorean major third on C is C-E while the just major third is C-E↓ (see Fig. 4 for "combined" symbol)
 Sagittal notation (from Latin ''sagitta'', "arrow") is a system of arrow-like accidentals that indicate prime-number comma alterations to tones in a Pythagorean series. It is used to notate both just intonation and equal temperaments. The size of the symbol indicates the size of the alteration.
The great advantage of such notation systems is that they allow the natural harmonic series to be precisely notated. At the same time, they provide some degree of practicality through their extension of staff notation, as traditionally trained performers may draw on their intuition for roughly estimating pitch height. This may be contrasted with the more abstract use of ratios for representing pitches in which the amount by which two pitches differ and the "direction" of change may not be immediately obvious to most musicians. One caveat is the requirement for performers to learn and internalize a (large) number of new graphical symbols. However, the use of unique symbols reduces harmonic ambiguity and the potential confusion arising from indicating only cent deviations.
Sagittal notation (from Latin ''sagitta'', "arrow") is a system of arrow-like accidentals that indicate prime-number comma alterations to tones in a Pythagorean series. It is used to notate both just intonation and equal temperaments. The size of the symbol indicates the size of the alteration.
The great advantage of such notation systems is that they allow the natural harmonic series to be precisely notated. At the same time, they provide some degree of practicality through their extension of staff notation, as traditionally trained performers may draw on their intuition for roughly estimating pitch height. This may be contrasted with the more abstract use of ratios for representing pitches in which the amount by which two pitches differ and the "direction" of change may not be immediately obvious to most musicians. One caveat is the requirement for performers to learn and internalize a (large) number of new graphical symbols. However, the use of unique symbols reduces harmonic ambiguity and the potential confusion arising from indicating only cent deviations.
Audio examples
* An A-major scale, followed by three major triads, and then a progression of fifths in just intonation. * An A-major scale, followed by three major triads, and then a progression of fifths in equal temperament. The beating in this file may be more noticeable after listening to the above file. * A pair of major thirds, followed by a pair of full major chords. The first in each pair is in equal temperament; the second is in just intonation. Piano sound. * A pair of major chords. The first is in equal temperament; the second is in just intonation. The pair of chords is repeated with a transition from equal temperament to just intonation between the two chords. In the equal temperament chords a roughness or beating can be heard at about 4 Hz and about 0.8 Hz. In the just intonation triad, this roughness is absent. Thesquare wave
A square wave is a non-sinusoidal periodic waveform in which the amplitude alternates at a steady frequency between fixed minimum and maximum values, with the same duration at minimum and maximum. In an ideal square wave, the transitions b ...
form makes the difference between equal temperament and just intonation more obvious.
See also
* List of compositions in just intonation *List of intervals in 5-limit just intonation The intervals of 5-limit just intonation (prime limit, not odd limit) are ratios involving only the powers of 2, 3, and 5. The fundamental intervals are the superparticular ratios 2/1 (the octave), 3/2 (the perfect fifth) and 5/4 (the major third ...
* List of meantone intervals
* List of pitch intervals
* Electronic tuner
* Hexany
*Microtonal music
Microtonal music or microtonality is the use in music of microtones— intervals smaller than a semitone, also called "microintervals". It may also be extended to include any music using intervals not found in the customary Western tuning of ...
*Microtuner
A microtuner or microtonal tuner is an electronic device or software program designed to modify and test the tuning of musical instruments (in particular synthesizers) with microtonal precision, allowing for the design and construction of microton ...
* Music and mathematics
*Musical interval
In music theory, an interval is a difference in pitch between two sounds.
An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or ha ...
* Pythagorean interval
* Regular number
* Superparticular ratio
* Whole-tone scale
References
External links
Art of the States: microtonal/just intonation
works using just intonation by American composers
Just Intonation
b
Mark Nowitzky
Just intonation
compared with meantone and 12-equal temperaments; a video featuring Pachelbel's canon.
Just Intonation Explained
by Kyle Gann
A selection of Just Intonation works edited by the Just Intonation Network
web published on the Tellus Audio Cassette Magazine project archive at UbuWeb
Medieval Music and Arts Foundation
* Barbieri, Patrizio
(2008) Latina, Il Levante
22 Note Just Intonation Keyboard Software with 12 Indian Instrument Sounds
Libreria Editrice
Plainsound Music Edition
– JI music and research, information about the Helmholtz-Ellis JI Pitch Notation {{Authority control *