|
Fundamental Frequency
The fundamental frequency, often referred to simply as the ''fundamental'' (abbreviated as 0 or 1 ), is defined as the lowest frequency of a Periodic signal, periodic waveform. In music, the fundamental is the musical pitch (music), pitch of a note that is perceived as the lowest Harmonic series (music)#Partial, partial present. In terms of a superposition of Sine wave, sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as 0, indicating the lowest frequency Zero-based numbering, counting from zero. In other contexts, it is more common to abbreviate it as 1, the first harmonic. (The second harmonic is then 2 = 2⋅1, etc.) According to Benward and Saker's ''Music: In Theory and Practice'': Explanation All sinusoidal and many non-sinusoidal waveforms repeat exactly over time – they are per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Partials On Strings
In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the ''fundamental frequency'' of a periodic signal. The fundamental frequency is also called the ''1st harmonic''; the other harmonics are known as ''higher harmonics''. As all harmonics are Periodic function, periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a ''harmonic series (music), harmonic series''. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hertz, Hz, a common alternating current, AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50& ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MIT Press
The MIT Press is the university press of the Massachusetts Institute of Technology (MIT), a private research university in Cambridge, Massachusetts. The MIT Press publishes a number of academic journals and has been a pioneer in the Open Access movement in academic publishing. History MIT Press traces its origins back to 1926 when MIT published a lecture series entitled ''Problems of Atomic Dynamics'' given by the visiting German physicist and later Nobel Prize winner, Max Born. In 1932, MIT's publishing operations were first formally instituted by the creation of an imprint called Technology Press. This imprint was founded by James R. Killian, Jr., at the time editor of MIT's alumni magazine and later to become MIT president. Technology Press published eight titles independently, then in 1937 entered into an arrangement with John Wiley & Sons in which Wiley took over marketing and editorial responsibilities. In 1961, the centennial of MIT's founding charter, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics technology may be called an Acoustical engineering, acoustical engineer. The application of acoustics is present in almost all aspects of modern society with the most obvious being the audio and noise control industries. Hearing (sense), Hearing is one of the most crucial means of survival in the animal world and speech is one of the most distinctive characteristics of human development and culture. Accordingly, the science of acoustics spreads across many facets of human society—music, medicine, architecture, industrial production, warfare and more. Likewise, animal species such as songbirds and frogs use sound and hearing as a key element of mating rituals or for marking territories. Art, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Tuning
In music, there are two common meanings for tuning: * #Tuning practice, Tuning practice, the act of tuning an instrument or voice. * #Tuning systems, Tuning systems, the various systems of Pitch (music), pitches used to tune an instrument, and their theoretical bases. Tuning practice Tuning is the process of adjusting the pitch of one or many tones from musical instruments to establish typical intervals between these tones. Tuning is usually based on a fixed reference, such as A440 (pitch standard), A = 440 Hz. The term "''out of tune''" refers to a pitch/tone that is either too high (Sharp (music), sharp) or too low (Flat (music), flat) in relation to a given reference pitch. While an instrument might be in tune relative to its own range of notes, it may not be considered 'in tune' if it does not match the chosen reference pitch. Some instruments become 'out of tune' with temperature, humidity, damage, or simply time, and must be readjusted or repaired. Different method ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Of Harmonics
The scale of harmonics is a musical scale based on the noded positions of the natural harmonics existing on a string. This musical scale is present on the guqin, regarded as one of the first string instruments with a musical scale.Yin, Wei. ''Zhongguo Qinshi Yanyi'' 【中国琴史演义】 (Chinese). Pages 1-10. Most fret positions appearing on Non-Western string instruments (lutes) are equal to positions of this scale. Unexpectedly, these fret positions are actually the corresponding undertones of the overtones from the harmonic series. The distance from the nut to the fret is an integer number lower than the distance from the fret to the bridge (see: superparticular number). Origin On the guqin, the left end of the dotted scale is a mirror image of the right end. The instrument is played with flageolet tones (harmonics) as well as pressing the strings on the wood. The flageolets appear on the harmonic positions of the overtone series, therefore these positions are marked a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pitch Detection Algorithm
A pitch detection algorithm (PDA) is an algorithm designed to estimate the pitch or fundamental frequency of a quasiperiodic or oscillating signal, usually a digital recording of speech or a musical note or tone. This can be done in the time domain, the frequency domain, or both. PDAs are used in various contexts (e.g. phonetics, music information retrieval, speech coding, musical performance systems) and so there may be different demands placed upon the algorithm. There is as yet no single ideal PDA, so a variety of algorithms exist, most falling broadly into the classes given below. A PDA typically estimates the period of a quasiperiodic signal, then inverts that value to give the frequency. General approaches One simple approach would be to measure the distance between zero crossing points of the signal (i.e. the zero-crossing rate). However, this does not work well with complicated waveforms which are composed of multiple sine waves with differing periods or noisy data. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscillation
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms. Oscillations occur not only in mechanical systems but also in dynamic systems in virtually every area of science: for example the beating of the human heart (for circulation), business cycles in economics, predator–prey population cycles in ecology, geothermal geysers in geology, vibration of strings in guitar and other string instruments, periodic firing of nerve cells in the brain, and the periodic swelling of Cepheid variable stars in astronomy. The term ''vibration'' is precisely used to describe a mechanical oscillation. Oscillation, especially rapid oscillation, may be an undesirable phenomenon in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Frequency
Natural frequency, measured in terms of '' eigenfrequency'', is the rate at which an oscillatory system tends to oscillate in the absence of disturbance. A foundational example pertains to simple harmonic oscillators, such as an idealized spring with no energy loss wherein the system exhibits constant-amplitude oscillations with a constant frequency. The phenomenon of resonance occurs when a forced vibration matches a system's natural frequency. Overview Free vibrations of an elastic body, also called ''natural vibrations'', occur at the natural frequency. Natural vibrations are different from forced vibrations which happen at the frequency of an applied force (forced frequency). If the forced frequency is equal to the natural frequency, the vibrations' amplitude increases manyfold. This phenomenon is known as resonance where the system's response to the applied frequency is amplified.. A system's ''normal mode'' is defined by the oscillation of a natural frequency in a sine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
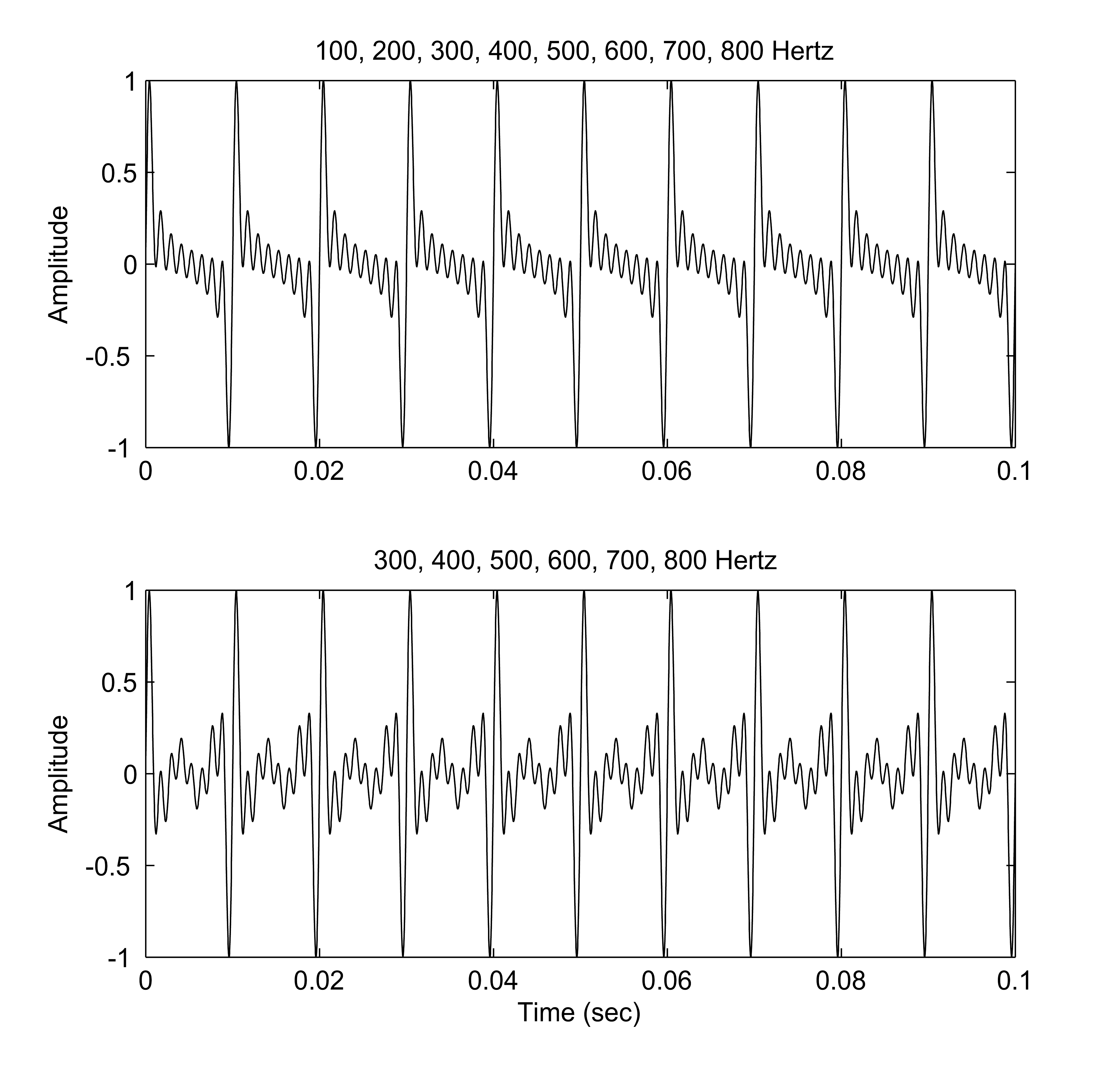
Missing Fundamental
The pitch being perceived with the first harmonic being absent in the waveform is called the missing fundamental phenomenon. It is established in psychoacoustics that the auditory system, with its natural tendency to distinguish a tone from another, will persistently assign a pitch to a complex tone given that a sufficient set of harmonics are present in the spectrum. For example, when a note (that is not a pure tone) has a pitch (music), pitch of 100 hertz, Hz, it will consist of frequency components that are integer multiples of that value (e.g. 100, 200, 300, 400, 500.... Hz). However, smaller loudspeakers may not produce low frequencies, so in our example, the 100 Hz component may be missing. Nevertheless, a pitch corresponding to the fundamental may still be heard. Explanation A low pitch (psychophysics), pitch (also known as the pitch of the missing fundamental or virtual pitch) can sometimes be heard when there is no apparent source or component of that frequ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greatest Common Divisor
In mathematics, the greatest common divisor (GCD), also known as greatest common factor (GCF), of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers , , the greatest common divisor of and is denoted \gcd (x,y). For example, the GCD of 8 and 12 is 4, that is, . In the name "greatest common divisor", the adjective "greatest" may be replaced by "highest", and the word "divisor" may be replaced by "factor", so that other names include highest common factor, etc. Historically, other names for the same concept have included greatest common measure. This notion can be extended to polynomials (see ''Polynomial greatest common divisor'') and other commutative rings (see ' below). Overview Definition The ''greatest common divisor'' (GCD) of integers and , at least one of which is nonzero, is the greatest positive integer such that is a divisor of both and ; that is, there are integers and such that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Analysis
Modal analysis is the study of the dynamic properties of systems in the frequency domain. It consists of mechanically exciting a studied component in such a way to target the Normal mode, modeshapes of the structure, and recording the vibration data with a network of sensors. Examples would include measuring the vibration of a car's body when it is attached to a shaker (testing device), shaker, or the White noise, noise pattern in a room when excited by a loudspeaker. Modern day experimental modal analysis systems are composed of 1) sensors such as transducers (typically accelerometers, load cells), or non contact via a Laser vibrometer, or Photogrammetry, stereophotogrammetric cameras 2) data acquisition system and an analog-to-digital converter front end (to digitize Analog signal, analog instrumentation signals) and 3) host PC (personal computer) to view the data and analyze it. Classically this was done with a SIMO (single-input, multiple-output) approach, that is, one excit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force. The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is. Calculations The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (DOF) (for example, stretching or compression of a rod), the stiffness is defined as k = \frac where, * F is the force on the body * \delta is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) Stiffness is usually defined under quasi-static conditions, but sometimes under dynamic loading. In the International System of Units, stiffness is typically measured in newtons per meter (N/m). In Imperial units, stiffness is typically measured in pounds (lbs) per inch. Generally speaking, deflections (or motions) of an infinitesima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |