Mass–energy Equivalence on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 Einstein did not write the exact formula in his 1905 ''Annus Mirabilis'' paper "Does the Inertia of an object Depend Upon Its Energy Content?"; rather, the paper states that if a body gives off the energy by emitting light, its mass diminishes by . This formulation relates only a change in mass to a change in energy without requiring the absolute relationship. The relationship convinced him that mass and energy can be seen as two names for the same underlying, conserved physical quantity. He has stated that the laws of conservation of energy and conservation of mass are "one and the same". Einstein elaborated in a 1946 essay that "the principle of the conservation of mass… proved inadequate in the face of the special theory of relativity. It was therefore merged with the energy conservation principle—just as, about 60 years before, the principle of the conservation of mechanical energy had been combined with the principle of the conservation of heat hermal energy We might say that the principle of the conservation of energy, having previously swallowed up that of the conservation of heat, now proceeded to swallow that of the conservation of mass—and holds the field alone."
Einstein did not write the exact formula in his 1905 ''Annus Mirabilis'' paper "Does the Inertia of an object Depend Upon Its Energy Content?"; rather, the paper states that if a body gives off the energy by emitting light, its mass diminishes by . This formulation relates only a change in mass to a change in energy without requiring the absolute relationship. The relationship convinced him that mass and energy can be seen as two names for the same underlying, conserved physical quantity. He has stated that the laws of conservation of energy and conservation of mass are "one and the same". Einstein elaborated in a 1946 essay that "the principle of the conservation of mass… proved inadequate in the face of the special theory of relativity. It was therefore merged with the energy conservation principle—just as, about 60 years before, the principle of the conservation of mechanical energy had been combined with the principle of the conservation of heat hermal energy We might say that the principle of the conservation of energy, having previously swallowed up that of the conservation of heat, now proceeded to swallow that of the conservation of mass—and holds the field alone."
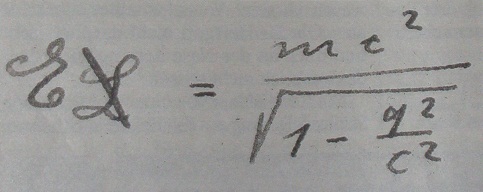 In developing
In developing
Einstein on the Inertia of Energy
– MathPages
Mass and Energy
– Conversations About Science with Theoretical Physicist
The Equivalence of Mass and Energy
– Entry in the ''Stanford Encyclopedia of Philosophy'' * {{DEFAULTSORT:Mass-Energy Equivalence 1905 introductions 1905 in science 1905 in Germany Albert Einstein Energy (physics) Equations Mass Special relativity
 In
In physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, mass–energy equivalence is the relationship between mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
and energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
in a system's rest frame
In special relativity, the rest frame of a particle is the frame of reference (a coordinate system attached to physical markers) in which the particle is at rest.
The rest frame of compound objects (such as a fluid, or a solid made of many vibrati ...
. The two differ only by a multiplicative constant and the units of measurement. The principle is described by the physicist Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
's formula: . In a reference frame
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system, whose origin, orientation, and scale have been specified in physical space. It is based on a set of reference points, defined as geometric ...
where the system is moving, its relativistic energy
Relativity may refer to:
Physics
* Galilean relativity, Galileo's conception of relativity
* Numerical relativity, a subfield of computational physics that aims to establish numerical solutions to Einstein's field equations in general relativity ...
and relativistic mass
The word "mass" has two meanings in special relativity: ''invariant mass'' (also called rest mass) is an invariant quantity which is the same for all observers in all reference frames, while the relativistic mass is dependent on the velocity ...
(instead of rest mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, ...
) obey the same formula.
The formula defines the energy () of a particle in its rest frame as the product of mass () with the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
squared (). Because the speed of light is a large number in everyday units (approximately ), the formula implies that a small amount of mass corresponds to an enormous amount of energy.
Rest mass, also called invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, ...
, is a fundamental physical property
A physical property is any property of a physical system that is measurable. The changes in the physical properties of a system can be used to describe its changes between momentary states. A quantifiable physical property is called ''physical ...
of matter
In classical physics and general chemistry, matter is any substance that has mass and takes up space by having volume. All everyday objects that can be touched are ultimately composed of atoms, which are made up of interacting subatomic pa ...
, independent of velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
. Massless particle
In particle physics, a massless particle is an elementary particle whose invariant mass is zero. At present the only confirmed massless particle is the photon.
Other particles and quasiparticles
Standard Model gauge bosons
The photon (carrier of ...
s such as photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s have zero invariant mass, but massless free particle
In physics, a free particle is a particle that, in some sense, is not bound by an external force, or equivalently not in a region where its potential energy varies. In classical physics, this means the particle is present in a "field-free" space. I ...
s have both momentum and energy.
The equivalence principle implies that when mass is lost in chemical reaction
A chemical reaction is a process that leads to the chemistry, chemical transformation of one set of chemical substances to another. When chemical reactions occur, the atoms are rearranged and the reaction is accompanied by an Gibbs free energy, ...
s or nuclear reaction
In nuclear physics and nuclear chemistry, a nuclear reaction is a process in which two atomic nucleus, nuclei, or a nucleus and an external subatomic particle, collide to produce one or more new nuclides. Thus, a nuclear reaction must cause a t ...
s, a corresponding amount of energy will be released. The energy can be released to the environment (outside of the system being considered) as radiant energy
In physics, and in particular as measured by radiometry, radiant energy is the energy of electromagnetic radiation, electromagnetic and gravitational radiation. As energy, its SI unit is the joule (J). The quantity of radiant energy may be calcul ...
, such as light
Light, visible light, or visible radiation is electromagnetic radiation that can be visual perception, perceived by the human eye. Visible light spans the visible spectrum and is usually defined as having wavelengths in the range of 400– ...
, or as thermal energy
The term "thermal energy" is often used ambiguously in physics and engineering. It can denote several different physical concepts, including:
* Internal energy: The energy contained within a body of matter or radiation, excluding the potential en ...
. The principle is fundamental to many fields of physics, including nuclear
Nuclear may refer to:
Physics
Relating to the nucleus of the atom:
*Nuclear engineering
*Nuclear physics
*Nuclear power
*Nuclear reactor
*Nuclear weapon
*Nuclear medicine
*Radiation therapy
*Nuclear warfare
Mathematics
* Nuclear space
*Nuclear ...
and particle physics
Particle physics or high-energy physics is the study of Elementary particle, fundamental particles and fundamental interaction, forces that constitute matter and radiation. The field also studies combinations of elementary particles up to the s ...
.
Mass–energy equivalence arose from special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between Spacetime, space and time. In Albert Einstein's 1905 paper, Annus Mirabilis papers#Special relativity,
"On the Ele ...
as a paradox
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true or apparently true premises, leads to a seemingly self-contradictor ...
described by the French polymath
A polymath or polyhistor is an individual whose knowledge spans many different subjects, known to draw on complex bodies of knowledge to solve specific problems. Polymaths often prefer a specific context in which to explain their knowledge, ...
Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...
(1854–1912). Einstein was the first to propose the equivalence of mass and energy as a general principle and a consequence of the symmetries of space and time. The principle first appeared in "Does the inertia of a body depend upon its energy-content?", one of his ''annus mirabilis'' papers, published on 21 November 1905. The formula and its relationship to momentum, as described by the energy–momentum relation
In physics, the energy–momentum relation, or relativistic dispersion relation, is the relativistic equation relating total energy (which is also called relativistic energy) to invariant mass (which is also called rest mass) and momentum. It i ...
, were later developed by other physicists.
Description
Mass–energy equivalence states that all objects havingmass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
, or ''massive objects'', have a corresponding intrinsic energy, even when they are stationary. In the rest frame
In special relativity, the rest frame of a particle is the frame of reference (a coordinate system attached to physical markers) in which the particle is at rest.
The rest frame of compound objects (such as a fluid, or a solid made of many vibrati ...
of an object, where by definition it is motionless and so has no momentum
In Newtonian mechanics, momentum (: momenta or momentums; more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. ...
, the mass and energy are equal or they differ only by a constant factor, the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
squared (). In Newtonian mechanics
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body r ...
, a motionless body has no kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
, and it may or may not have other amounts of internal stored energy, like chemical energy
Chemical energy is the energy of chemical substances that is released when the substances undergo a chemical reaction and transform into other substances. Some examples of storage media of chemical energy include batteries, Schmidt-Rohr, K. (20 ...
or thermal energy
The term "thermal energy" is often used ambiguously in physics and engineering. It can denote several different physical concepts, including:
* Internal energy: The energy contained within a body of matter or radiation, excluding the potential en ...
, in addition to any potential energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity ...
it may have from its position in a field of force. These energies tend to be much smaller than the mass of the object multiplied by , which is on the order of 1017 joule
The joule ( , or ; symbol: J) is the unit of energy in the International System of Units (SI). In terms of SI base units, one joule corresponds to one kilogram- metre squared per second squared One joule is equal to the amount of work d ...
s for a mass of one kilogram. By this principle, the mass of the atoms that come out of a nuclear reaction
In nuclear physics and nuclear chemistry, a nuclear reaction is a process in which two atomic nucleus, nuclei, or a nucleus and an external subatomic particle, collide to produce one or more new nuclides. Thus, a nuclear reaction must cause a t ...
is less than the mass of the atoms that go in, and the difference in mass shows up as heat and light with the same equivalent energy as the difference. In analyzing these extreme events, Einstein's formula can be used with as the energy released (removed), and as the change in mass.
In relativity, all the energy that moves with an object (i.e., the energy as measured in the object's rest frame) contributes to the total mass of the body, which measures how much it resists acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector ...
. If an isolated box of ideal mirrors could contain light, the individually massless photons would contribute to the total mass of the box by the amount equal to their energy divided by . For an observer in the rest frame, removing energy is the same as removing mass, and the formula indicates how much mass is lost when energy is removed. In the same way, when any energy is added to an isolated system, the increase in the mass is equal to the added energy divided by .
Mass in special relativity
An object moves at different speeds in differentframes of reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system, whose origin, orientation, and scale have been specified in physical space. It is based on a set of reference points, defined as geometric ...
, depending on the motion of the observer. This implies the kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
, in both Newtonian mechanics and relativity, is 'frame dependent', so that the amount of relativistic energy that an object is measured to have depends on the observer. The ''relativistic mass'' of an object is given by the relativistic energy divided by . Because the relativistic mass is exactly proportional to the relativistic energy, relativistic mass and relativistic energy are nearly synonym
A synonym is a word, morpheme, or phrase that means precisely or nearly the same as another word, morpheme, or phrase in a given language. For example, in the English language, the words ''begin'', ''start'', ''commence'', and ''initiate'' are a ...
ous; the only difference between them is the units
Unit may refer to:
General measurement
* Unit of measurement, a definite magnitude of a physical quantity, defined and adopted by convention or by law
**International System of Units (SI), modern form of the metric system
**English units, histo ...
. The ''rest mass'' or invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, ...
of an object is defined as the mass an object has in its rest frame, when it is not moving with respect to the observer. The rest mass is the same for all inertial frame
In classical physics and special relativity, an inertial frame of reference (also called an inertial space or a Galilean reference frame) is a frame of reference in which objects exhibit inertia: they remain at rest or in uniform motion relative ...
s, as it is independent of the motion of the observer, it is the smallest possible value of the relativistic mass of the object. Because of the attraction between components of a system, which results in potential energy, the rest mass is almost never additive
Additive may refer to:
Mathematics
* Additive function, a function in number theory
* Additive map, a function that preserves the addition operation
* Additive set-function see Sigma additivity
* Additive category, a preadditive category with fin ...
; in general, the mass of an object is not the sum of the masses of its parts. The rest mass of an object is the total energy of all the parts, including kinetic energy, as observed from the center of momentum frame, and potential energy. The masses add up only if the constituents are at rest (as observed from the center of momentum frame) and do not attract or repel, so that they do not have any extra kinetic or potential energy.They can also have a positive kinetic energy and a negative potential energy that exactly cancels. Massless particles are particles with no rest mass, and therefore have no intrinsic energy; their energy is due only to their momentum.
Relativistic mass
Relativistic mass depends on the motion of the object, so that different observers in relative motion see different values for it. The relativistic mass of a moving object is larger than the relativistic mass of an object at rest, because a moving object has kinetic energy. If the object moves slowly, the relativistic mass is nearly equal to therest mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, ...
and both are nearly equal to the classical inertial mass (as it appears in Newton's laws of motion
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body re ...
). If the object moves quickly, the relativistic mass is greater than the rest mass by an amount equal to the mass associated with the kinetic energy of the object. Massless particles also have relativistic mass derived from their kinetic energy, equal to their relativistic energy divided by , or . The speed of light is one in a system where length and time are measured in natural units
In physics, natural unit systems are measurement systems for which selected physical constants have been set to 1 through nondimensionalization of physical units. For example, the speed of light may be set to 1, and it may then be omitted, equa ...
and the relativistic mass and energy would be equal in value and dimension. As it is just another name for the energy, the use of the term ''relativistic mass'' is redundant and physicists generally reserve ''mass'' to refer to rest mass, or invariant mass, as opposed to relativistic mass. A consequence of this terminology is that the mass is not conserved in special relativity, whereas the conservation of momentum and conservation of energy
The law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be Conservation law, ''conserved'' over time. In the case of a Closed system#In thermodynamics, closed system, the principle s ...
are both fundamental laws.
Conservation of mass and energy
Conservation of energy is a universal principle in physics and holds for any interaction, along with the conservation of momentum. The classical conservation of mass, in contrast, is violated in certain relativistic settings. This concept has been experimentally proven in a number of ways, including the conversion of mass into kinetic energy in nuclear reactions and other interactions betweenelementary particle
In particle physics, an elementary particle or fundamental particle is a subatomic particle that is not composed of other particles. The Standard Model presently recognizes seventeen distinct particles—twelve fermions and five bosons. As a c ...
s. While modern physics has discarded the expression 'conservation of mass', in older terminology a relativistic mass
The word "mass" has two meanings in special relativity: ''invariant mass'' (also called rest mass) is an invariant quantity which is the same for all observers in all reference frames, while the relativistic mass is dependent on the velocity ...
can also be defined to be equivalent to the energy of a moving system, allowing for a ''conservation of relativistic mass''. Mass conservation breaks down when the energy associated with the mass of a particle is converted into other forms of energy, such as kinetic energy, thermal energy, or radiant energy
In physics, and in particular as measured by radiometry, radiant energy is the energy of electromagnetic radiation, electromagnetic and gravitational radiation. As energy, its SI unit is the joule (J). The quantity of radiant energy may be calcul ...
.
Massless particles
Massless particles have zero rest mass. ThePlanck–Einstein relation
The Planck relationFrench & Taylor (1978), pp. 24, 55.Cohen-Tannoudji, Diu & Laloë (1973/1977), pp. 10–11. (referred to as Planck's energy–frequency relation,Schwinger (2001), p. 203. the Planck–Einstein relation, Planck equation, and Plan ...
for the energy for photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s is given by the equation , where is the Planck constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a ...
and is the photon frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
. This frequency and thus the relativistic energy are frame-dependent. If an observer runs away from a photon in the direction the photon travels from a source, and it catches up with the observer, the observer sees it as having less energy than it had at the source. The faster the observer is traveling with regard to the source when the photon catches up, the less energy the photon would be seen to have. As an observer approaches the speed of light with regard to the source, the redshift
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation (such as light). The opposite change, a decrease in wavelength and increase in frequency and e ...
of the photon increases, according to the relativistic Doppler effect
The relativistic Doppler effect is the change in frequency, wavelength and amplitude of light, caused by the relative motion of the source and the observer (as in the classical Doppler effect, first proposed by Christian Doppler in 1842), when ta ...
. The energy of the photon is reduced and as the wavelength becomes arbitrarily large, the photon's energy approaches zero, because of the massless nature of photons, which does not permit any intrinsic energy.
Composite systems
For closed systems made up of many parts, like anatomic nucleus
The atomic nucleus is the small, dense region consisting of protons and neutrons at the center of an atom, discovered in 1911 by Ernest Rutherford at the Department_of_Physics_and_Astronomy,_University_of_Manchester , University of Manchester ...
, planet, or star, the relativistic energy is given by the sum of the relativistic energies of each of the parts, because energies are additive in these systems. If a system is ''bound'' by attractive forces, and the energy gained in excess of the work done is removed from the system, then mass is lost with this removed energy. The mass of an atomic nucleus is less than the total mass of the proton
A proton is a stable subatomic particle, symbol , Hydron (chemistry), H+, or 1H+ with a positive electric charge of +1 ''e'' (elementary charge). Its mass is slightly less than the mass of a neutron and approximately times the mass of an e ...
s and neutron
The neutron is a subatomic particle, symbol or , that has no electric charge, and a mass slightly greater than that of a proton. The Discovery of the neutron, neutron was discovered by James Chadwick in 1932, leading to the discovery of nucle ...
s that make it up. This mass decrease is also equivalent to the energy required to break up the nucleus into individual protons and neutrons. This effect can be understood by looking at the potential energy of the individual components. The individual particles have a force attracting them together, and forcing them apart increases the potential energy of the particles in the same way that lifting an object up on earth does. This energy is equal to the work required to split the particles apart. The mass of the Solar System
The Solar SystemCapitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Sola ...
is slightly less than the sum of its individual masses.
For an isolated system of particles moving in different directions, the invariant mass of the system is the analog of the rest mass, and is the same for all observers, even those in relative motion. It is defined as the total energy (divided by ) in the center of momentum frame
In physics, the center-of-momentum frame (COM frame) of a system, also known as zero-momentum frame, is the inertial frame in which the total momentum of the system vanishes. It is unique up to velocity, but not origin. The ''center of momentum'' ...
. The ''center of momentum frame'' is defined so that the system has zero total momentum; the term center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weight function, weighted relative position (vector), position of the d ...
frame is also sometimes used, where the ''center of mass frame'' is a special case of the center of momentum frame where the center of mass is put at the origin. A simple example of an object with moving parts but zero total momentum is a container of gas. In this case, the mass of the container is given by its total energy (including the kinetic energy of the gas molecules), since the system's total energy and invariant mass are the same in any reference frame where the momentum is zero, and such a reference frame is also the only frame in which the object can be weighed. In a similar way, the theory of special relativity posits that the thermal energy in all objects, including solids, contributes to their total masses, even though this energy is present as the kinetic and potential energies of the atoms in the object, and it (in a similar way to the gas) is not seen in the rest masses of the atoms that make up the object. Similarly, even photons, if trapped in an isolated container, would contribute their energy to the mass of the container. Such extra mass, in theory, could be weighed in the same way as any other type of rest mass, even though individually photons have no rest mass. The property that trapped energy in any form adds weighable mass to systems that have no net momentum is one of the consequences of relativity. It has no counterpart in classical Newtonian physics, where energy never exhibits weighable mass.
Relation to gravity
Physics has two concepts of mass, the gravitational mass and the inertial mass. The gravitational mass is the quantity that determines the strength of thegravitational field
In physics, a gravitational field or gravitational acceleration field is a vector field used to explain the influences that a body extends into the space around itself. A gravitational field is used to explain gravitational phenomena, such as ...
generated by an object, as well as the gravitational force acting on the object when it is immersed in a gravitational field produced by other bodies. The inertial mass, on the other hand, quantifies how much an object accelerates if a given force is applied to it. The mass–energy equivalence in special relativity refers to the inertial mass. However, already in the context of Newtonian gravity, the weak equivalence principle
The equivalence principle is the hypothesis that the observed equivalence of gravitational and inertial mass is a consequence of nature. The weak form, known for centuries, relates to masses of any composition in free fall taking the same t ...
is postulated: the gravitational and the inertial mass of every object are the same. Thus, the mass–energy equivalence, combined with the weak equivalence principle, results in the prediction that all forms of energy contribute to the gravitational field generated by an object. This observation is one of the pillars of the general theory of relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physi ...
.
The prediction that all forms of energy interact gravitationally has been subject to experimental tests. One of the first observations testing this prediction, called the Eddington experiment
The Eddington experiment was an observational test of general relativity, organised by the British astronomers Frank Watson Dyson and Arthur Stanley Eddington in 1919. The observations were of the total solar eclipse of 29 May 1919 and were ca ...
, was made during the solar eclipse of May 29, 1919
A total solar eclipse occurred at the Moon's descending node of orbit on Thursday, May 29, 1919, with a magnitude of 1.0719. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of ...
. During the eclipse, the English astronomer
An astronomer is a scientist in the field of astronomy who focuses on a specific question or field outside the scope of Earth. Astronomers observe astronomical objects, such as stars, planets, natural satellite, moons, comets and galaxy, galax ...
and physicist Arthur Eddington
Sir Arthur Stanley Eddington, (28 December 1882 – 22 November 1944) was an English astronomer, physicist, and mathematician. He was also a philosopher of science and a populariser of science. The Eddington limit, the natural limit to the lu ...
observed that the light from stars passing close to the Sun was bent. The effect is due to the gravitational attraction of light by the Sun. The observation confirmed that the energy carried by light indeed is equivalent to a gravitational mass. Another seminal experiment, the Pound–Rebka experiment, was performed in 1960. In this test a beam of light was emitted from the top of a tower and detected at the bottom. The frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
of the light detected was higher than the light emitted. This result confirms that the energy of photons increases when they fall in the gravitational field of the Earth. The energy, and therefore the gravitational mass, of photons is proportional to their frequency as stated by the Planck's relation.
Efficiency
In some reactions, matter particles can be destroyed and their associated energy released to the environment as other forms of energy, such as light and heat. One example of such a conversion takes place in elementary particle interactions, where the rest energy is transformed into kinetic energy. Such conversions between types of energy happen in nuclear weapons, in which the protons and neutrons inatomic nuclei
The atomic nucleus is the small, dense region consisting of protons and neutrons at the center of an atom, discovered in 1911 by Ernest Rutherford at the University of Manchester based on the 1909 Geiger–Marsden gold foil experiment. Aft ...
lose a small fraction of their original mass, though the mass lost is not due to the destruction of any smaller constituents. Nuclear fission
Nuclear fission is a reaction in which the nucleus of an atom splits into two or more smaller nuclei. The fission process often produces gamma photons, and releases a very large amount of energy even by the energetic standards of radioactiv ...
allows a tiny fraction of the energy associated with the mass to be converted into usable energy such as radiation; in the decay of the uranium
Uranium is a chemical element; it has chemical symbol, symbol U and atomic number 92. It is a silvery-grey metal in the actinide series of the periodic table. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons. Ura ...
, for instance, about 0.1% of the mass of the original atom is lost. In theory, it should be possible to destroy matter and convert all of the rest-energy associated with matter into heat and light, but none of the theoretically known methods are practical. One way to harness all the energy associated with mass is to annihilate matter with antimatter
In modern physics, antimatter is defined as matter composed of the antiparticles (or "partners") of the corresponding subatomic particle, particles in "ordinary" matter, and can be thought of as matter with reversed charge and parity, or go ...
. Antimatter is rare in the universe, however, and the known mechanisms of production require more usable energy than would be released in annihilation. CERN
The European Organization for Nuclear Research, known as CERN (; ; ), is an intergovernmental organization that operates the largest particle physics laboratory in the world. Established in 1954, it is based in Meyrin, western suburb of Gene ...
estimated in 2011 that over a billion
Billion is a word for a large number, and it has two distinct definitions:
* 1,000,000,000, i.e. one thousand million, or (ten to the ninth power), as defined on the short scale. This is now the most common sense of the word in all varieties of ...
times more energy is required to make and store antimatter than could be released in its annihilation.
As most of the mass which comprises ordinary objects resides in protons and neutrons, converting all the energy of ordinary matter into more useful forms requires that the protons and neutrons be converted to lighter particles, or particles with no mass at all. In the Standard Model of particle physics
The Standard Model of particle physics is the theory describing three of the four known fundamental forces (electromagnetic, weak and strong interactions – excluding gravity) in the universe and classifying all known elementary particles. It ...
, the number of protons plus neutrons is nearly exactly conserved. Despite this, Gerard 't Hooft
Gerardus "Gerard" 't Hooft (; born July 5, 1946) is a Dutch theoretical physicist and professor at Utrecht University, the Netherlands. He shared the 1999 Nobel Prize in Physics with his thesis advisor Martinus J. G. Veltman "for elucidating t ...
showed that there is a process that converts protons and neutrons to antielectron
The positron or antielectron is the particle with an electric charge of +1'' e'', a spin of 1/2 (the same as the electron), and the same mass as an electron. It is the antiparticle (antimatter counterpart) of the electron. When a positron col ...
s and neutrino
A neutrino ( ; denoted by the Greek letter ) is an elementary particle that interacts via the weak interaction and gravity. The neutrino is so named because it is electrically neutral and because its rest mass is so small ('' -ino'') that i ...
s. This is the weak SU(2)
In mathematics, the special unitary group of degree , denoted , is the Lie group of unitary matrices with determinant 1.
The matrices of the more general unitary group may have complex determinants with absolute value 1, rather than real 1 ...
instanton
An instanton (or pseudoparticle) is a notion appearing in theoretical and mathematical physics. An instanton is a classical solution to equations of motion with a finite, non-zero action, either in quantum mechanics or in quantum field theory. M ...
proposed by the physicists Alexander Belavin, Alexander Markovich Polyakov
Alexander Markovich Polyakov (; born 27 September 1945) is a Russian theoretical physicist, formerly at the Landau Institute in Moscow and, since 1989, at Princeton University, where he is the Joseph Henry Professor of Physics Emeritus.
Importa ...
, Albert Schwarz
Albert Solomonovich Schwarz ( ; ; born June 24, 1934) is a Soviet and American mathematician and a theoretical physicist educated in the Soviet Union and now a professor at the University of California, Davis.
Early life and education
Schwarz was ...
, and Yu. S. Tyupkin. This process, can in principle destroy matter and convert all the energy of matter into neutrinos and usable energy, but it is normally extraordinarily slow. It was later shown that the process occurs rapidly at extremely high temperatures that would only have been reached shortly after the Big Bang
The Big Bang is a physical theory that describes how the universe expanded from an initial state of high density and temperature. Various cosmological models based on the Big Bang concept explain a broad range of phenomena, including th ...
.
Many extensions of the standard model contain magnetic monopole
In particle physics, a magnetic monopole is a hypothetical particle that is an isolated magnet with only one magnetic pole (a north pole without a south pole or vice versa). A magnetic monopole would have a net north or south "magnetic charge". ...
s, and in some models of grand unification
A Grand Unified Theory (GUT) is any model in particle physics that merges the electromagnetic, weak, and strong forces (the three gauge interactions of the Standard Model) into a single force at high energies. Although this unified force ha ...
, these monopoles catalyze proton decay
In particle physics, proton decay is a hypothetical form of particle decay in which the proton decays into lighter subatomic particles, such as a neutral pion and a positron. The proton decay hypothesis was first formulated by Andrei Sakharov ...
, a process known as the Callan–Rubakov effect. This process would be an efficient mass–energy conversion at ordinary temperatures, but it requires making monopoles and anti-monopoles, whose production is expected to be inefficient. Another method of completely annihilating matter uses the gravitational field of black holes. The British theoretical physicist
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain, and predict natural phenomena. This is in contrast to experimental physics, which uses experi ...
Stephen Hawking
Stephen William Hawking (8January 194214March 2018) was an English theoretical physics, theoretical physicist, cosmologist, and author who was director of research at the Centre for Theoretical Cosmology at the University of Cambridge. Between ...
theorized it is possible to throw matter into a black hole and use the emitted heat to generate power. According to the theory of Hawking radiation
Hawking radiation is black-body radiation released outside a black hole's event horizon due to quantum effects according to a model developed by Stephen Hawking in 1974.
The radiation was not predicted by previous models which assumed that onc ...
, however, larger black holes radiate less than smaller ones, so that usable power can only be produced by small black holes.
Extension for systems in motion
Unlike a system's energy in an inertial frame, the relativistic energy () of a system depends on both the rest mass () and the total momentum of the system. The extension of Einstein's equation to these systems is given by:Some authors state the expression equivalently as where is theLorentz factor
The Lorentz factor or Lorentz term (also known as the gamma factor) is a dimensionless quantity expressing how much the measurements of time, length, and other physical properties change for an object while it moves. The expression appears in sev ...
.
or
or
where the term represents the square of the Euclidean norm
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' ...
(total vector length) of the various momentum vectors in the system, which reduces to the square of the simple momentum magnitude, if only a single particle is considered. This equation is called the energy–momentum relation
In physics, the energy–momentum relation, or relativistic dispersion relation, is the relativistic equation relating total energy (which is also called relativistic energy) to invariant mass (which is also called rest mass) and momentum. It i ...
and reduces to when the momentum term is zero. For photons where , the equation reduces to .
Low-speed approximation
Using theLorentz factor
The Lorentz factor or Lorentz term (also known as the gamma factor) is a dimensionless quantity expressing how much the measurements of time, length, and other physical properties change for an object while it moves. The expression appears in sev ...
, , the energy–momentum can be rewritten as and expanded as a power series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a co ...
:
For speeds much smaller than the speed of light, higher-order terms in this expression get smaller and smaller because is small. For low speeds, all but the first two terms can be ignored:
In classical mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics inv ...
, both the term and the high-speed corrections are ignored. The initial value of the energy is arbitrary, as only the change in energy can be measured and so the term is ignored in classical physics. While the higher-order terms become important at higher speeds, the Newtonian equation is a highly accurate low-speed approximation; adding in the third term yields:
.
The difference between the two approximations is given by , a number very small for everyday objects. In 2018 NASA announced the Parker Solar Probe
The Parker Solar Probe (PSP; previously Solar Probe, Solar Probe Plus or Solar Probe+) is a NASA space probe launched in 2018 to make observations of the Stellar corona, Sun's outer corona.
It used repeated Gravity assist, gravity assists from ...
was the fastest ever, with a speed of . The difference between the approximations for the Parker Solar Probe in 2018 is , which accounts for an energy correction of four parts per hundred million. The gravitational constant
The gravitational constant is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's general relativity, theory of general relativity. It ...
, in contrast, has a standard relative uncertainty
Uncertainty or incertitude refers to situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown, and is particularly relevant for decision ...
of about .
Applications
Application to nuclear physics
Thenuclear binding energy
Nuclear binding energy in experimental physics is the minimum energy that is required to disassemble the nucleus of an atom into its constituent protons and neutrons, known collectively as nucleons. The binding energy for stable nuclei is alwa ...
is the minimum energy that is required to disassemble the nucleus of an atom into its component parts. The mass of an atom is less than the sum of the masses of its constituents due to the attraction of the strong nuclear force
In nuclear physics and particle physics, the strong interaction, also called the strong force or strong nuclear force, is one of the four known fundamental interactions. It confines quarks into protons, neutrons, and other hadron particles, an ...
. The difference between the two masses is called the ''mass defect'' and is related to the binding energy through Einstein's formula. The principle is used in modeling nuclear fission reactions, and it implies that a great amount of energy can be released by the nuclear fission chain reaction
A chain reaction is a sequence of reactions where a reactive product or by-product causes additional reactions to take place. In a chain reaction, positive feedback leads to a self-amplifying chain of events.
Chain reactions are one way that sys ...
s used in both nuclear weapon
A nuclear weapon is an explosive device that derives its destructive force from nuclear reactions, either fission (fission or atomic bomb) or a combination of fission and fusion reactions (thermonuclear weapon), producing a nuclear exp ...
s and nuclear power
Nuclear power is the use of nuclear reactions to produce electricity. Nuclear power can be obtained from nuclear fission, nuclear decay and nuclear fusion reactions. Presently, the vast majority of electricity from nuclear power is produced by ...
.
A water molecule weighs a little less than two free hydrogen atoms and an oxygen atom. The minuscule mass difference is the energy needed to split the molecule into three individual atoms (divided by ), which was given off as heat when the molecule formed (this heat had mass). Similarly, a stick of dynamite in theory weighs a little bit more than the fragments after the explosion; in this case the mass difference is the energy and heat that is released when the dynamite explodes. Such a change in mass may only happen when the system is open, and the energy and mass are allowed to escape. Thus, if a stick of dynamite is detonated in a hermetically sealed chamber, the mass of the chamber and fragments, the heat, sound, and light would still be equal to the original mass of the chamber and dynamite. If sitting on a scale, the weight and mass would not change. This would in theory also happen even with a nuclear bomb, if it could be kept in an ideal box of infinite strength, which did not rupture or pass radiation
In physics, radiation is the emission or transmission of energy in the form of waves or particles through space or a material medium. This includes:
* ''electromagnetic radiation'' consisting of photons, such as radio waves, microwaves, infr ...
. Thus, a 21.5 kiloton
TNT equivalent is a convention for expressing energy, typically used to describe the energy released in an explosion. A ton of TNT equivalent is a unit of energy defined by convention to be (). It is the approximate energy released in the det ...
() nuclear bomb produces about one gram of heat and electromagnetic radiation, but the mass of this energy would not be detectable in an exploded bomb in an ideal box sitting on a scale; instead, the contents of the box would be heated to millions of degrees without changing total mass and weight. If a transparent window passing only electromagnetic radiation were opened in such an ideal box after the explosion, and a beam of X-rays and other lower-energy light allowed to escape the box, it would eventually be found to weigh one gram less than it had before the explosion. This weight loss and mass loss would happen as the box was cooled by this process, to room temperature. However, any surrounding mass that absorbed the X-rays (and other "heat") would ''gain'' this gram of mass from the resulting heating, thus, in this case, the mass "loss" would represent merely its relocation.
Practical examples
Einstein used thecentimetre–gram–second system of units
The centimetre–gram–second system of units (CGS or cgs) is a variant of the metric system based on the centimetre as the unit of length, the gram as the unit of mass, and the second as the unit of time. All CGS mechanical units are unamb ...
(cgs), but the formula is independent of the system of units. In natural units, the numerical value of the speed of light is set to equal 1, and the formula expresses an equality of numerical values: . In the SI system (expressing the ratio in joules
The joule ( , or ; symbol: J) is the unit of energy in the International System of Units (SI). In terms of SI base units, one joule corresponds to one kilogram- metre squared per second squared One joule is equal to the amount of work don ...
per kilogram using the value of in metres per second
The metre per second is the unit of both speed (a scalar quantity) and velocity (a vector quantity, which has direction and magnitude) in the International System of Units (SI), equal to the speed of a body covering a distance of one metre in ...
):
: (≈ 9.0 × 1016 joules per kilogram).
So the energy equivalent of one kilogram of mass is
* 89.9 petajoules
The joule ( , or ; symbol: J) is the unit of energy in the International System of Units (SI). In terms of SI base units, one joule corresponds to one kilogram- metre squared per second squared One joule is equal to the amount of work done ...
* 25.0 billion
Billion is a word for a large number, and it has two distinct definitions:
* 1,000,000,000, i.e. one thousand million, or (ten to the ninth power), as defined on the short scale. This is now the most common sense of the word in all varieties of ...
kilowatt-hour
A kilowatt-hour ( unit symbol: kW⋅h or kW h; commonly written as kWh) is a non-SI unit of energy equal to 3.6 megajoules (MJ) in SI units, which is the energy delivered by one kilowatt of power for one hour. Kilowatt-hours are a comm ...
s (or 25,000 GW·h
A kilowatt-hour (unit symbol: kW⋅h or kW h; commonly written as kWh) is a non-SI unit of energy equal to 3.6 megajoules (MJ) in SI units, which is the energy delivered by one kilowatt of power for one hour. Kilowatt-hours are a common b ...
)
* 21.5 trillion
''Trillion'' is a number with two distinct definitions:
*1,000,000,000,000, i.e. one million 1,000,000, million, or (ten to the twelfth Exponentiation, power), as defined on the long and short scales, short scale. This is now the meaning in bot ...
kilocalories
The calorie is a unit of energy that originated from the caloric theory of heat. The large calorie, food calorie, dietary calorie, kilocalorie, or kilogram calorie is defined as the amount of heat needed to raise the temperature of one liter o ...
(or 21.5 Pcal)Conversions used: 1956 International (Steam) Table (IT) values where one calorie ≡ 4.1868 J and one BTU ≡ 1055.05585262 J. Weapons designers' conversion value of one gram TNT ≡ 1000 calories used.
* 85.2 trillion BTUs (or 0.0852 quads
The quadriceps femoris muscle (, also called the quadriceps extensor, quadriceps or quads) is a large muscle group that includes the four prevailing muscles on the front of the thigh. It is the sole extensor muscle of the knee, forming a large ...
)
:or the energy released by combustion of any of the following:
* 21 500 kiloton
TNT equivalent is a convention for expressing energy, typically used to describe the energy released in an explosion. A ton of TNT equivalent is a unit of energy defined by convention to be (). It is the approximate energy released in the det ...
s of TNT-equivalent energy (or 21.5 Mt)
* litre
The litre ( Commonwealth spelling) or liter ( American spelling) (SI symbols L and l, other symbol used: ℓ) is a metric unit of volume. It is equal to 1 cubic decimetre (dm3), 1000 cubic centimetres (cm3) or 0.001 cubic metres (m3). A ...
s or US gallon
The gallon is a unit of volume in British imperial units and United States customary units.
The imperial gallon (imp gal) is defined as , and is or was used in the United Kingdom and its former colonies, including Ireland, Canada, Australia ...
s of automotive gasoline
Gasoline ( North American English) or petrol ( Commonwealth English) is a petrochemical product characterized as a transparent, yellowish, and flammable liquid normally used as a fuel for spark-ignited internal combustion engines. When for ...
Any time energy is released, the process can be evaluated from an perspective. For instance, the "gadget"-style bomb used in the Trinity test
Trinity was the first detonation of a nuclear weapon, conducted by the United States Army at 5:29 a.m. MWT (11:29:21 GMT) on July 16, 1945, as part of the Manhattan Project. The test was of an implosion-design plutonium bomb, or "gadg ...
and the bombing of Nagasaki
On 6 and 9 August 1945, the United States detonated two atomic bombs over the Japanese cities of Hiroshima and Nagasaki, respectively, during World War II. The aerial bombings killed between 150,000 and 246,000 people, most of whom were civil ...
had an explosive yield equivalent to 21 kt of TNT. About 1 kg of the approximately 6.15 kg of plutonium
Plutonium is a chemical element; it has symbol Pu and atomic number 94. It is a silvery-gray actinide metal that tarnishes when exposed to air, and forms a dull coating when oxidized. The element normally exhibits six allotropes and four ...
in each of these bombs fissioned into lighter elements totaling almost exactly one gram less, after cooling. The electromagnetic radiation and kinetic energy (thermal and blast energy) released in this explosion carried the missing gram of mass.
Whenever energy is added to a system, the system gains mass, as shown when the equation is rearranged:
* A spring's mass increases whenever it is put into compression or tension. Its mass increase arises from the increased potential energy stored within it, which is bound in the stretched chemical (electron) bonds linking the atoms within the spring.
* Raising the temperature of an object (increasing its thermal energy
The term "thermal energy" is often used ambiguously in physics and engineering. It can denote several different physical concepts, including:
* Internal energy: The energy contained within a body of matter or radiation, excluding the potential en ...
) increases its mass. For example, consider the world's primary mass standard for the kilogram, made of platinum
Platinum is a chemical element; it has Symbol (chemistry), symbol Pt and atomic number 78. It is a density, dense, malleable, ductility, ductile, highly unreactive, precious metal, precious, silverish-white transition metal. Its name origina ...
and iridium
Iridium is a chemical element; it has the symbol Ir and atomic number 77. This very hard, brittle, silvery-white transition metal of the platinum group, is considered the second-densest naturally occurring metal (after osmium) with a density ...
. If its temperature is allowed to change by 1 °C, its mass changes by 1.5 picograms (1 pg = ).Assuming a 90/10 alloy of Pt/Ir by weight, a of 25.9 for Pt and 25.1 for Ir, a Pt-dominated average of 25.8, 5.134 moles of metal, and 132 J⋅K−1 for the prototype. A variation of ±1.5 picograms is much smaller than the uncertainty in the mass of the international prototype, which is ±2 micrograms.
* A spinning ball has greater mass than when it is not spinning. Its increase of mass is exactly the equivalent of the mass of energy of rotation, which is itself the sum of the kinetic energies of all the moving parts of the ball. For example, the Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all of Earth's water is ...
itself is more massive due to its rotation, than it would be with no rotation. The rotational energy of the Earth is greater than 1024 Joules, which is over 107 kg.
History
WhileEinstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
was the first to have correctly deduced the mass–energy equivalence formula, he was not the first to have related energy with mass, though nearly all previous authors thought that the energy that contributes to mass comes only from electromagnetic fields. Once discovered, Einstein's formula was initially written in many different notations, and its interpretation and justification was further developed in several steps.
Developments prior to Einstein
Eighteenth century theories on the correlation of mass and energy included that devised by the English scientistIsaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
in 1717, who speculated that light particles and matter particles were interconvertible in "Query 30" of the ''Opticks
''Opticks: or, A Treatise of the Reflexions, Refractions, Inflexions and Colours of Light'' is a collection of three books by Isaac Newton that was published in English language, English in 1704 (a scholarly Latin translation appeared in 1706). ...
'', where he asks: "Are not the gross bodies and light convertible into one another, and may not bodies receive much of their activity from the particles of light which enter their composition?" Swedish scientist and theologian Emanuel Swedenborg
Emanuel Swedenborg (; ; born Emanuel Swedberg; (29 January 168829 March 1772) was a Swedish polymath; scientist, engineer, astronomer, anatomist, Christian theologian, philosopher, and mysticism, mystic. He became best known for his book on the ...
, in his ''Principia
Principia may refer to:
* ''Philosophiæ Naturalis Principia Mathematica'', Isaac Newton's three-volume work about his laws of motion and universal gravitation
* Principia ( "primary buildings"), the headquarters at the center of Roman forts ()
* ...
'' of 1734 theorized that all matter is ultimately composed of dimensionless points of "pure and total motion". He described this motion as being without force, direction or speed, but having the potential for force, direction and speed everywhere within it.
During the nineteenth century there were several speculative attempts to show that mass and energy were proportional in various ether theories. In 1873 the Russian physicist and mathematician Nikolay Umov
Nikolay Alekseevich Umov (; January 23, 1846 – January 15, 1915) was a Russian physicist and mathematician known for discovering the concept of Umov-Poynting vector and Umov effect.
Biography
Umov was born in 1846 in Simbirsk (present-day U ...
pointed out a relation between mass and energy for ether in the form of , where . English engineer Samuel Tolver Preston
Samuel Tolver Preston (8 July 1844 – 1917) was an English engineer and physicist.
His parents were Daniel Bloom Preston (born 1807) and Mary Susannah Tolver. Preston was educated as a Telegraph-engineer. He went to Munich, where he attained hi ...
in 1875 and the Italian industrialist and geologist
A geologist is a scientist who studies the structure, composition, and History of Earth, history of Earth. Geologists incorporate techniques from physics, chemistry, biology, mathematics, and geography to perform research in the Field research, ...
Olinto De Pretto
Olinto De Pretto (26 April 1857 – 16 March 1921) was an Italian industrialist and geologist from Schio, Vicenza. It is claimed by an Italian mathematician, Umberto Bartocci, that De Pretto may have been the first person to derive the energy– ...
in 1903, following physicist Georges-Louis Le Sage
Georges-Louis Le Sage (; 13 June 1724 – 20 November 1803) was a Genevan physicist and is most known for his theory of gravitation, for his invention of an electric telegraph and his anticipation of the kinetic theory of gases. He was a cont ...
, imagined that the universe was filled with an ether
In organic chemistry, ethers are a class of compounds that contain an ether group, a single oxygen atom bonded to two separate carbon atoms, each part of an organyl group (e.g., alkyl or aryl). They have the general formula , where R and R� ...
of tiny particles that always move at speed . Each of these particles has a kinetic energy of up to a small numerical factor, giving a mass–energy relation.
In 1905, independently of Einstein, French polymath Gustave Le Bon
Charles-Marie Gustave Le Bon (7 May 1841 – 13 December 1931) was a leading French polymath whose areas of interest included anthropology, psychology, sociology, medicine, invention, and physics. He is best known for his 1895 work '' The Crowd: ...
speculated that atoms could release large amounts of latent energy, reasoning from an all-encompassing qualitative philosophy of physics
In philosophy, the philosophy of physics deals with conceptual and interpretational issues in physics, many of which overlap with research done by certain kinds of theoretical physicists. Historically, philosophers of physics have engaged with ...
.
Electromagnetic mass
There were many attempts in the 19th and the beginning of the 20th century—like those of British physicistsJ. J. Thomson
Sir Joseph John Thomson (18 December 1856 – 30 August 1940) was an English physicist who received the Nobel Prize in Physics in 1906 "in recognition of the great merits of his theoretical and experimental investigations on the conduction of ...
in 1881 and Oliver Heaviside
Oliver Heaviside ( ; 18 May 1850 – 3 February 1925) was an English mathematician and physicist who invented a new technique for solving differential equations (equivalent to the Laplace transform), independently developed vector calculus, an ...
in 1889, and George Frederick Charles Searle in 1897, German physicists Wilhelm Wien
Wilhelm Carl Werner Otto Fritz Franz Wien (; 13 January 1864 – 30 August 1928) was a German physicist who used theories about heat and electromagnetism to deduce Wien's displacement law, which calculates the emission of a blackbody at any te ...
in 1900 and Max Abraham
Max Abraham (; 26 March 1875 – 16 November 1922) was a German physicist known for his work on electromagnetism and his opposition to the theory of relativity.
Biography
Abraham was born in Danzig, Imperial Germany (now Gdańsk in Poland) ...
in 1902, and the Dutch physicist Hendrik Antoon Lorentz
Hendrik Antoon Lorentz ( ; ; 18 July 1853 – 4 February 1928) was a Dutch theoretical physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for their discovery and theoretical explanation of the Zeeman effect. He derived ...
in 1904—to understand how the mass of a charged object depends on the electrostatic field
An electric field (sometimes called E-field) is a physical field that surrounds electrically charged particles such as electrons. In classical electromagnetism, the electric field of a single charge (or group of charges) describes their capac ...
. This concept was called electromagnetic mass
Electromagnetic mass was initially a concept of classical mechanics, denoting as to how much the electromagnetic field, or the self-energy, is contributing to the mass of charged particles. It was first derived by J. J. Thomson in 1881 and was ...
, and was considered as being dependent on velocity and direction as well. Lorentz in 1904 gave the following expressions for longitudinal and transverse electromagnetic mass:
where
Another way of deriving a type of electromagnetic mass was based on the concept of radiation pressure
Radiation pressure (also known as light pressure) is mechanical pressure exerted upon a surface due to the exchange of momentum between the object and the electromagnetic field. This includes the momentum of light or electromagnetic radiation of ...
. In 1900, French polymath Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...
associated electromagnetic radiation energy with a "fictitious fluid" having momentum and mass
By that, Poincaré tried to save the center of mass theorem in Lorentz's theory, though his treatment led to radiation paradoxes.
Austrian physicist Friedrich Hasenöhrl
Friedrich Hasenöhrl (; 30 November 1874 – 7 October 1915) was an Austrian physicist and professor of the University of Vienna. He postulated a relation between electromagnetic mass and energy, close to the modern mass–energy equivalence.
He ...
showed in 1904 that electromagnetic cavity radiation contributes the "apparent mass"
to the cavity's mass. He argued that this implies mass dependence on temperature as well.
Einstein: mass–energy equivalence
 Einstein did not write the exact formula in his 1905 ''Annus Mirabilis'' paper "Does the Inertia of an object Depend Upon Its Energy Content?"; rather, the paper states that if a body gives off the energy by emitting light, its mass diminishes by . This formulation relates only a change in mass to a change in energy without requiring the absolute relationship. The relationship convinced him that mass and energy can be seen as two names for the same underlying, conserved physical quantity. He has stated that the laws of conservation of energy and conservation of mass are "one and the same". Einstein elaborated in a 1946 essay that "the principle of the conservation of mass… proved inadequate in the face of the special theory of relativity. It was therefore merged with the energy conservation principle—just as, about 60 years before, the principle of the conservation of mechanical energy had been combined with the principle of the conservation of heat hermal energy We might say that the principle of the conservation of energy, having previously swallowed up that of the conservation of heat, now proceeded to swallow that of the conservation of mass—and holds the field alone."
Einstein did not write the exact formula in his 1905 ''Annus Mirabilis'' paper "Does the Inertia of an object Depend Upon Its Energy Content?"; rather, the paper states that if a body gives off the energy by emitting light, its mass diminishes by . This formulation relates only a change in mass to a change in energy without requiring the absolute relationship. The relationship convinced him that mass and energy can be seen as two names for the same underlying, conserved physical quantity. He has stated that the laws of conservation of energy and conservation of mass are "one and the same". Einstein elaborated in a 1946 essay that "the principle of the conservation of mass… proved inadequate in the face of the special theory of relativity. It was therefore merged with the energy conservation principle—just as, about 60 years before, the principle of the conservation of mechanical energy had been combined with the principle of the conservation of heat hermal energy We might say that the principle of the conservation of energy, having previously swallowed up that of the conservation of heat, now proceeded to swallow that of the conservation of mass—and holds the field alone."
Mass–velocity relationship
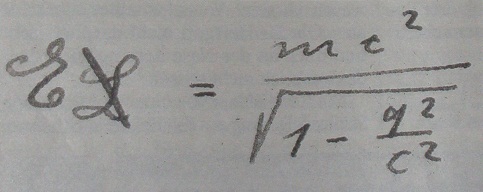 In developing
In developing special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between Spacetime, space and time. In Albert Einstein's 1905 paper, Annus Mirabilis papers#Special relativity,
"On the Ele ...
, Einstein found that the kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
of a moving body is
with the velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
, the rest mass, and the Lorentz factor.
He included the second term on the right to make sure that for small velocities the energy would be the same as in classical mechanics, thus satisfying the correspondence principle
In physics, a correspondence principle is any one of several premises or assertions about the relationship between classical and quantum mechanics.
The physicist Niels Bohr coined the term in 1920 during the early development of quantum theory; ...
:
Without this second term, there would be an additional contribution in the energy when the particle is not moving.
Einstein's view on mass
Einstein, following Lorentz and Abraham, used velocity- and direction-dependent mass concepts in his 1905 electrodynamics paper and in another paper in 1906. In Einstein's first 1905 paper on , he treated as what would now be called the ''rest mass'', and it has been noted that in his later years he did not like the idea of "relativistic mass". In modern physics terminology, relativistic energy is used in lieu of relativistic mass and the term "mass" is reserved for the rest mass. Historically, there has been considerable debate over the use of the concept of "relativistic mass" and the connection of "mass" in relativity to "mass" in Newtonian dynamics. One view is that only rest mass is a viable concept and is a property of the particle; while relativistic mass is a conglomeration of particle properties and properties of spacetime. Another view, attributed to Norwegian physicist Kjell Vøyenli, is that the Newtonian concept of mass as a particle property and the relativistic concept of mass have to be viewed as embedded in their own theories and as having no precise connection.Einstein's 1905 derivation
Already in his relativity paper "On the electrodynamics of moving bodies", Einstein derived the correct expression for the kinetic energy of particles: Now the question remained open as to which formulation applies to bodies at rest. This was tackled by Einstein in his paper "Does the inertia of a body depend upon its energy content?", one of his Annus Mirabilis papers. Here, Einstein used to represent the speed of light in vacuum and to represent theenergy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
lost by a body in the form of radiation. Consequently, the equation was not originally written as a formula but as a sentence in German saying that "if a body gives off the energy in the form of radiation, its mass diminishes by ." A remark placed above it informed that the equation was approximated by neglecting "magnitudes of fourth and higher orders" of a series expansion
In mathematics, a series expansion is a technique that expresses a Function (mathematics), function as an infinite sum, or Series (mathematics), series, of simpler functions. It is a method for calculating a Function (mathematics), function that ...
.See the sentence on the last page 641 of the original German edition, above the equation
. See also the sentence above the last equation in the English translation, , and the comment on the symbols used in ''About this edition'' that follows the translation. Einstein used a body emitting two light pulses in opposite directions, having energies of before and after the emission as seen in its rest frame. As seen from a moving frame, becomes and becomes . Einstein obtained, in modern notation:
He then argued that can only differ from the kinetic energy by an additive constant, which gives
Neglecting effects higher than third order in after a Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
expansion of the right side of this yields:
Einstein concluded that the emission reduces the body's mass by , and that the mass of a body is a measure of its energy content.
The correctness of Einstein's 1905 derivation of was criticized by German theoretical physicist Max Planck
Max Karl Ernst Ludwig Planck (; ; 23 April 1858 – 4 October 1947) was a German Theoretical physics, theoretical physicist whose discovery of energy quantum, quanta won him the Nobel Prize in Physics in 1918.
Planck made many substantial con ...
in 1907, who argued that it is only valid to first approximation. Another criticism was formulated by American physicist Herbert Ives in 1952 and the Israeli physicist Max Jammer
Max Jammer (; born Moshe Jammer, ; 13 April 1915 – 18 December 2010), was an Israeli physicist and philosophy of physics, philosopher of physics. He was born in Berlin, Germany. He was Rector and Acting President at Bar-Ilan University from 19 ...
in 1961, asserting that Einstein's derivation is based on begging the question
In classical rhetoric and logic, begging the question or assuming the conclusion (Latin: ) is an informal fallacy that occurs when an argument's premises assume the truth of the conclusion. Historically, begging the question refers to a fault i ...
. Other scholars, such as American and Chilean philosopher
Philosophy ('love of wisdom' in Ancient Greek) is a systematic study of general and fundamental questions concerning topics like existence, reason, knowledge, Value (ethics and social sciences), value, mind, and language. It is a rational an ...
s John Stachel
John Stachel (; March 29, 1928 – May 9, 2025) was an American physicist and philosopher of science.
Life and career
Stachel earned his PhD at Stevens Institute of Technology in Physics about a topic in General relativity in 1958. After holding d ...
and Roberto Torretti
Roberto Torretti (February 15, 1930 – November 12, 2022) was a Chilean philosopher, author and academic who was internationally renowned for his contributions to the history of philosophy, philosophy of physics and philosophy of mathematics.
B ...
, have argued that Ives' criticism was wrong, and that Einstein's derivation was correct. American physics writer Hans Ohanian, in 2008, agreed with Stachel/Torretti's criticism of Ives, though he argued that Einstein's derivation was wrong for other reasons.
Relativistic center-of-mass theorem of 1906
Like Poincaré, Einstein concluded in 1906 that the inertia of electromagnetic energy is a necessary condition for the center-of-mass theorem to hold. On this occasion, Einstein referred to Poincaré's 1900 paper and wrote: "Although the merely formal considerations, which we will need for the proof, are already mostly contained in a work by H. Poincaré2, for the sake of clarity I will not rely on that work." In Einstein's more physical, as opposed to formal or mathematical, point of view, there was no need for fictitious masses. He could avoid the ''perpetual motion
Perpetual motion is the motion of bodies that continues forever in an unperturbed system. A perpetual motion machine is a hypothetical machine that can do work indefinitely without an external energy source. This kind of machine is impossible ...
'' problem because, on the basis of the mass–energy equivalence, he could show that the transport of inertia that accompanies the emission and absorption of radiation solves the problem. Poincaré's rejection of the principle of action–reaction can be avoided through Einstein's , because mass conservation appears as a special case of the energy conservation law
The law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be Conservation law, ''conserved'' over time. In the case of a Closed system#In thermodynamics, closed system, the principle s ...
.
Further developments
There were several further developments in the first decade of the twentieth century. In May 1907, Einstein explained that the expression for energy of a moving mass point assumes the simplest form when its expression for the state of rest is chosen to be (where is the mass), which is in agreement with the "principle of the equivalence of mass and energy". In addition, Einstein used the formula , with being the energy of a system of mass points, to describe the energy and mass increase of that system when the velocity of the differently moving mass points is increased. Max Planck rewrote Einstein's mass–energy relationship as in June 1907, where is the pressure and the volume to express the relation between mass, its latent energy, and thermodynamic energy within the body. Subsequently, in October 1907, this was rewritten as and given a quantum interpretation by German physicistJohannes Stark
Johannes Stark (; 15 April 1874 – 21 June 1957) was a German physicist who received the Nobel Prize in Physics in 1919 "for his discovery of the Doppler effect in canal rays and the splitting of spectral lines in electric fields". This phenom ...
, who assumed its validity and correctness. In December 1907, Einstein expressed the equivalence in the form and concluded: "A mass is equivalent, as regards inertia, to a quantity of energy . ��It appears far more natural to consider every inertial mass as a store of energy." American physical chemist
Physical chemistry is the study of macroscopic and microscopic phenomena in chemical systems in terms of the principles, practices, and concepts of physics such as motion, energy, force, time, thermodynamics, quantum chemistry, statistical mecha ...
s Gilbert N. Lewis
Gilbert Newton Lewis (October 23 or October 25, 1875 – March 23, 1946) was an American physical chemist and a dean of the college of chemistry at University of California, Berkeley. Lewis was best known for his discovery of the covalent bon ...
and Richard C. Tolman
Richard Chace Tolman (March 4, 1881 – September 5, 1948) was an American mathematical physicist and physical chemist who made many contributions to statistical mechanics and theoretical cosmology. He was a professor at the California Ins ...
used two variations of the formula in 1909: and , with being the relativistic energy (the energy of an object when the object is moving), is the rest energy (the energy when not moving), is the relativistic mass (the rest mass and the extra mass gained when moving), and is the rest mass. The same relations in different notation were used by Lorentz in 1913 and 1914, though he placed the energy on the left-hand side: and , with being the total energy (rest energy plus kinetic energy) of a moving material point, its rest energy, the relativistic mass, and the invariant mass.
In 1911, German physicist Max von Laue
Max Theodor Felix von Laue (; 9 October 1879 – 24 April 1960) was a German physicist who received the Nobel Prize in Physics in 1914 "for his discovery of the X-ray diffraction, diffraction of X-rays by crystals".
In addition to his scientifi ...
gave a more comprehensive proof of from the stress–energy tensor
The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity that describes the density and flux of energy and momentum in spacetime, generalizing the stress ...
, which was later generalized by German mathematician Felix Klein
Felix Christian Klein (; ; 25 April 1849 – 22 June 1925) was a German mathematician and Mathematics education, mathematics educator, known for his work in group theory, complex analysis, non-Euclidean geometry, and the associations betwe ...
in 1918.
Einstein returned to the topic once again after World War II
World War II or the Second World War (1 September 1939 – 2 September 1945) was a World war, global conflict between two coalitions: the Allies of World War II, Allies and the Axis powers. World War II by country, Nearly all of the wo ...
and this time he wrote in the title of his article intended as an explanation for a general reader by analogy.
Alternative version
An alternative version of Einstein'sthought experiment
A thought experiment is an imaginary scenario that is meant to elucidate or test an argument or theory. It is often an experiment that would be hard, impossible, or unethical to actually perform. It can also be an abstract hypothetical that is ...
was proposed by American theoretical physicist Fritz Rohrlich
Fritz Rohrlich (May 12, 1921 – November 14, 2018) was an American theoretical physicist and educator who published in the fields of quantum electrodynamics, classical electrodynamics of charged particles, and the philosophy of science.
Life an ...
in 1990, who based his reasoning on the Doppler effect
The Doppler effect (also Doppler shift) is the change in the frequency of a wave in relation to an observer who is moving relative to the source of the wave. The ''Doppler effect'' is named after the physicist Christian Doppler, who described ...
. Like Einstein, he considered a body at rest with mass . If the body is examined in a frame moving with nonrelativistic velocity , it is no longer at rest and in the moving frame it has momentum . Then he supposed the body emits two pulses of light to the left and to the right, each carrying an equal amount of energy . In its rest frame, the object remains at rest after the emission since the two beams are equal in strength and carry opposite momentum. However, if the same process is considered in a frame that moves with velocity to the left, the pulse moving to the left is redshift
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation (such as light). The opposite change, a decrease in wavelength and increase in frequency and e ...
ed, while the pulse moving to the right is blue shift
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation (such as light). The opposite change, a decrease in wavelength and increase in frequency and e ...
ed. The blue light carries more momentum than the red light, so that the momentum of the light in the moving frame is not balanced: the light is carrying some net momentum to the right. The object has not changed its velocity before or after the emission. Yet in this frame it has lost some right-momentum to the light. The only way it could have lost momentum is by losing mass. This also solves Poincaré's radiation paradox. The velocity is small, so the right-moving light is blueshifted by an amount equal to the nonrelativistic Doppler shift
The Doppler effect (also Doppler shift) is the change in the frequency of a wave in relation to an observer who is moving relative to the source of the wave. The ''Doppler effect'' is named after the physicist Christian Doppler, who described t ...
factor . The momentum of the light is its energy divided by , and it is increased by a factor of . So the right-moving light is carrying an extra momentum given by:
The left-moving light carries a little less momentum, by the same amount . So the total right-momentum in both light pulses is twice . This is the right-momentum that the object lost.
The momentum of the object in the moving frame after the emission is reduced to this amount:
So the change in the object's mass is equal to the total energy lost divided by . Since any emission of energy can be carried out by a two-step process, where first the energy is emitted as light and then the light is converted to some other form of energy, any emission of energy is accompanied by a loss of mass. Similarly, by considering absorption, a gain in energy is accompanied by a gain in mass.
Radioactivity and nuclear energy
It was quickly noted after the discovery ofradioactivity
Radioactive decay (also known as nuclear decay, radioactivity, radioactive disintegration, or nuclear disintegration) is the process by which an unstable atomic nucleus loses energy by radiation. A material containing unstable nuclei is conside ...
in 1897 that the total energy due to radioactive processes is about one million times greater than that involved in any known molecular change, raising the question of where the energy comes from. After eliminating the idea of absorption and emission of some sort of Lesagian ether particles, the existence of a huge amount of latent energy, stored within matter, was proposed by New Zealand physicist Ernest Rutherford
Ernest Rutherford, 1st Baron Rutherford of Nelson (30 August 1871 – 19 October 1937) was a New Zealand physicist who was a pioneering researcher in both Atomic physics, atomic and nuclear physics. He has been described as "the father of nu ...
and British radiochemist Frederick Soddy
Frederick Soddy FRS (2 September 1877 – 22 September 1956) was an English radiochemist who explained, with Ernest Rutherford, that radioactivity is due to the transmutation of elements, now known to involve nuclear reactions. He also pr ...
in 1903. Rutherford also suggested that this internal energy is stored within normal matter as well. He went on to speculate in 1904: "If it were ever found possible to control at will the rate of disintegration of the radio-elements, an enormous amount of energy could be obtained from a small quantity of matter."
Einstein's equation does not explain the large energies released in radioactive decay, but can be used to quantify them. The theoretical explanation for radioactive decay is given by the nuclear force
The nuclear force (or nucleon–nucleon interaction, residual strong force, or, historically, strong nuclear force) is a force that acts between hadrons, most commonly observed between protons and neutrons of atoms. Neutrons and protons, both ...
s responsible for holding atoms together, though these forces were still unknown in 1905. The enormous energy released from radioactive decay had previously been measured by Rutherford and was much more easily measured than the small change in the gross mass of materials as a result. Einstein's equation, by theory, can give these energies by measuring mass differences before and after reactions, but in practice, these mass differences in 1905 were still too small to be measured in bulk. Prior to this, the ease of measuring radioactive decay energies with a calorimeter
A calorimeter is a device used for calorimetry, or the process of measuring the heat of chemical reactions or physical changes as well as heat capacity. Differential scanning calorimeters, isothermal micro calorimeters, titration calorimeters ...
was thought possibly likely to allow measurement of changes in mass difference, as a check on Einstein's equation itself. Einstein mentions in his 1905 paper that mass–energy equivalence might perhaps be tested with radioactive decay, which was known by then to release enough energy to possibly be "weighed," when missing from the system. However, radioactivity seemed to proceed at its own unalterable pace, and even when simple nuclear reactions became possible using proton bombardment, the idea that these great amounts of usable energy could be liberated at will with any practicality, proved difficult to substantiate. Rutherford was reported in 1933 to have declared that this energy could not be exploited efficiently: "Anyone who expects a source of power from the transformation of the atom is talking moonshine
Moonshine is alcohol proof, high-proof liquor, traditionally made or distributed alcohol law, illegally. The name was derived from a tradition of distilling the alcohol (drug), alcohol at night to avoid detection. In the first decades of the ...
."
This outlook changed dramatically in 1932 with the discovery of the neutron and its mass, allowing mass differences for single nuclide
Nuclides (or nucleides, from nucleus, also known as nuclear species) are a class of atoms characterized by their number of protons, ''Z'', their number of neutrons, ''N'', and their nuclear energy state.
The word ''nuclide'' was coined by the A ...
s and their reactions to be calculated directly, and compared with the sum of masses for the particles that made up their composition. In 1933, the energy released from the reaction of lithium-7
Naturally occurring lithium (3Li) is composed of two stable isotopes, lithium-6 (6Li) and lithium-7 (7Li), with the latter being far more abundant on Earth. Both of the natural isotopes have an unexpectedly low nuclear binding energy per nucle ...
plus protons giving rise to two alpha particle
Alpha particles, also called alpha rays or alpha radiation, consist of two protons and two neutrons bound together into a particle identical to a helium-4 nucleus. They are generally produced in the process of alpha decay but may also be produce ...
s, allowed Einstein's equation to be tested to an error of ±0.5%. However, scientists still did not see such reactions as a practical source of power, due to the energy cost of accelerating reaction particles. After the very public demonstration of huge energies released from nuclear fission after the atomic bombings of Hiroshima and Nagasaki
On 6 and 9 August 1945, the United States detonated two atomic bombs over the Japanese cities of Hiroshima and Nagasaki, respectively, during World War II. The aerial bombings killed between 150,000 and 246,000 people, most of whom were civili ...
in 1945, the equation became directly linked in the public eye with the power and peril of nuclear weapons. The equation was featured on page 2 of the Smyth Report
The Smyth Report (officially ''Atomic Energy for Military Purposes'') is the common name of an administrative history written by American physicist Henry DeWolf Smyth about the Manhattan Project, the Allies of World War II, Allied effort to ...
, the official 1945 release by the US government on the development of the atomic bomb, and by 1946 the equation was linked closely enough with Einstein's work that the cover of ''Time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ...
'' magazine prominently featured a picture of Einstein next to an image of a mushroom cloud
A mushroom cloud is a distinctive mushroom-shaped flammagenitus cloud of debris, smoke, and usually condensed water vapour resulting from a large explosion. The effect is most commonly associated with a nuclear explosion, but any sufficiently e ...
emblazoned with the equation. Einstein himself had only a minor role in the Manhattan Project
The Manhattan Project was a research and development program undertaken during World War II to produce the first nuclear weapons. It was led by the United States in collaboration with the United Kingdom and Canada.
From 1942 to 1946, the ...
: he had cosigned a letter to the U.S. president in 1939 urging funding for research into atomic energy, warning that an atomic bomb was theoretically possible. The letter persuaded Roosevelt to devote a significant portion of the wartime budget to atomic research. Without a security clearance, Einstein's only scientific contribution was an analysis of an isotope separation
Isotope separation is the process of concentrating specific isotopes of a chemical element by removing other isotopes. The use of the nuclides produced is varied. The largest variety is used in research (e.g. in chemistry where atoms of "marker" n ...
method in theoretical terms. It was inconsequential, on account of Einstein not being given sufficient information to fully work on the problem.
While is useful for understanding the amount of energy potentially released in a fission reaction, it was not strictly necessary to develop the weapon, once the fission process was known, and its energy measured at 200 MeV
In physics, an electronvolt (symbol eV), also written electron-volt and electron volt, is the measure of an amount of kinetic energy gained by a single electron accelerating through an electric potential difference of one volt in vacuum. When us ...
(which was directly possible, using a quantitative Geiger counter
A Geiger counter (, ; also known as a Geiger–Müller counter or G-M counter) is an electronic instrument for detecting and measuring ionizing radiation with the use of a Geiger–Müller tube. It is widely used in applications such as radiat ...
, at that time). The physicist and Manhattan Project participant Robert Serber
Robert Serber (March 14, 1909 – June 1, 1997) was an American physicist who participated in the Manhattan Project. Serber's lectures explaining the basic principles and goals of the project were printed and supplied to all incoming scientific st ...
noted that somehow "the popular notion took hold long ago that Einstein's theory of relativity, in particular his equation , plays some essential role in the theory of fission. Einstein had a part in alerting the United States government to the possibility of building an atomic bomb, but his theory of relativity is not required in discussing fission. The theory of fission is what physicists call a non-relativistic theory, meaning that relativistic effects are too small to affect the dynamics of the fission process significantly." There are other views on the equation's importance to nuclear reactions. In late 1938, the Austrian-Swedish and British physicists Lise Meitner
Elise Lise Meitner ( ; ; 7 November 1878 – 27 October 1968) was an Austrian-Swedish nuclear physicist who was instrumental in the discovery of nuclear fission.
After completing her doctoral research in 1906, Meitner became the second woman ...
and Otto Robert Frisch
Otto Robert Frisch (1 October 1904 – 22 September 1979) was an Austrian-born British physicist who worked on nuclear physics. With Otto Stern and Immanuel Estermann, he first measured the magnetic moment of the proton. With his aunt, Lise M ...
—while on a winter walk during which they solved the meaning of Hahn's experimental results and introduced the idea that would be called atomic fission—directly used Einstein's equation to help them understand the quantitative energetics of the reaction that overcame the "surface tension-like" forces that hold the nucleus together, and allowed the fission fragments to separate to a configuration from which their charges could force them into an energetic ''fission''. To do this, they used ''packing fraction'', or nuclear binding energy
In physics and chemistry, binding energy is the smallest amount of energy required to remove a particle from a system of particles or to disassemble a system of particles into individual parts. In the former meaning the term is predominantly use ...
values for elements. These, together with use of allowed them to realize on the spot that the basic fission process was energetically possible.
Einstein's equation written
According to the Einstein Papers Project at theCalifornia Institute of Technology
The California Institute of Technology (branded as Caltech) is a private research university in Pasadena, California, United States. The university is responsible for many modern scientific advancements and is among a small group of institutes ...
and Hebrew University of Jerusalem
The Hebrew University of Jerusalem (HUJI; ) is an Israeli public university, public research university based in Jerusalem. Co-founded by Albert Einstein and Chaim Weizmann in July 1918, the public university officially opened on 1 April 1925. ...
, there remain only four known copies of this equation as written by Einstein. One of these is a letter written in German
German(s) may refer to:
* Germany, the country of the Germans and German things
**Germania (Roman era)
* Germans, citizens of Germany, people of German ancestry, or native speakers of the German language
** For citizenship in Germany, see also Ge ...
to Ludwik Silberstein
Ludwik Silberstein (May 17, 1872 – January 17, 1948) was a Polish-American physicist who helped make special relativity and general relativity staples of university coursework. His textbook '' The Theory of Relativity'' was published by Macmill ...
, which was in Silberstein's archives, and sold at auction
An auction is usually a process of Trade, buying and selling Good (economics), goods or Service (economics), services by offering them up for Bidding, bids, taking bids, and then selling the item to the highest bidder or buying the item from th ...
for $1.2 million, RR Auction of Boston, Massachusetts
Boston is the capital and most populous city in the Commonwealth (U.S. state), Commonwealth of Massachusetts in the United States. The city serves as the cultural and Financial centre, financial center of New England, a region of the Northeas ...
said on May 21, 2021.
See also
Notes
References
External links
Einstein on the Inertia of Energy
– MathPages
Mass and Energy
– Conversations About Science with Theoretical Physicist
Matt Strassler
Matthew J. Strassler is a theoretical physicist, science communicator, and educator known for the cascading gauge theory.
Education
Strassler studied at Simon's Rock College and Princeton University, and further obtained his Ph.D from Stanford ...
The Equivalence of Mass and Energy
– Entry in the ''Stanford Encyclopedia of Philosophy'' * {{DEFAULTSORT:Mass-Energy Equivalence 1905 introductions 1905 in science 1905 in Germany Albert Einstein Energy (physics) Equations Mass Special relativity