The Global Positioning System (GPS) is a
satellite-based hyperbolic navigation system owned by the
United States Space Force
The United States Space Force (USSF) is the space force branch of the United States Department of Defense. It is one of the six United States Armed Forces, armed forces of the United States and one of the eight uniformed services of the Unite ...
and operated by
Mission Delta 31.
It is one of the
global navigation satellite systems (GNSS) that provide
geolocation
Geopositioning is the process of determining or estimating the geographic position of an object or a person.
Geopositioning yields a set of Geographic coordinate system, geographic coordinates (such as latitude and longitude) in a given map datum ...
and
time information to a
GPS receiver anywhere on or near the Earth where there is an unobstructed line of sight to four or more GPS satellites. It does not require the user to transmit any data, and operates independently of any telephone or Internet reception, though these technologies can enhance the usefulness of the GPS positioning information. It provides critical positioning capabilities to military, civil, and commercial users around the world. Although the United States government created, controls, and maintains the GPS system, it is freely accessible to anyone with a GPS receiver.
Overview
The GPS project was started by the
U.S. Department of Defense in 1973.
The first prototype spacecraft was launched in 1978 and the full constellation of 24 satellites became operational in 1993.
After
Korean Air Lines Flight 007 was shot down when it mistakenly entered Soviet airspace, President
Ronald Reagan
Ronald Wilson Reagan (February 6, 1911 – June 5, 2004) was an American politician and actor who served as the 40th president of the United States from 1981 to 1989. He was a member of the Republican Party (United States), Republican Party a ...
determined that the GPS system would be made available for civilian use as of 1988;
however, initially this civilian use was limited to an average accuracy of by use of
Selective Availability (SA), a deliberate error introduced into the GPS data that military receivers could correct for.
As civilian GPS usage grew, there was increasing pressure to remove this error. The SA system was temporarily disabled during the
Gulf War
, combatant2 =
, commander1 =
, commander2 =
, strength1 = Over 950,000 soldiers3,113 tanks1,800 aircraft2,200 artillery systems
, page = https://www.govinfo.gov/content/pkg/GAOREPORTS-PEMD-96- ...
, as a shortage of military GPS units meant that many US soldiers were using civilian GPS units sent from home. In the 1990s,
Differential GPS
Differential Global Positioning Systems (DGPSs) supplement and enhance the positional data available from global navigation satellite systems (GNSSs). A DGPS can increase accuracy of positional data by about a thousandfold, from approximately to ...
systems from the
US Coast Guard,
Federal Aviation Administration
The Federal Aviation Administration (FAA) is a Federal government of the United States, U.S. federal government agency within the United States Department of Transportation, U.S. Department of Transportation that regulates civil aviation in t ...
, and similar agencies in other countries began to broadcast local GPS corrections, reducing the effect of both SA degradation and atmospheric effects (that military receivers also corrected for). The U.S. military had also developed methods to perform local GPS jamming, meaning that the ability to globally degrade the system was no longer necessary. As a result, United States President
Bill Clinton
William Jefferson Clinton (né Blythe III; born August 19, 1946) is an American politician and lawyer who was the 42nd president of the United States from 1993 to 2001. A member of the Democratic Party (United States), Democratic Party, ...
signed a bill ordering that Selective Availability be disabled on May 1, 2000;
and, in 2007, the US government announced that the next generation of GPS satellites would not include the feature at all.
Advances in technology and new demands on the existing system have now led to efforts to modernize the GPS and implement the next generation of
GPS Block III satellites and Next Generation Operational Control System (OCX)
which was authorized by the
U.S. Congress in 2000. When Selective Availability was discontinued, GPS was accurate to about . GPS receivers that use the L5 band have much higher accuracy of , while those for high-end applications such as engineering and land surveying are accurate to within and can even provide sub-millimeter accuracy with long-term measurements.
Consumer devices such as smartphones can be accurate to or better when used with assistive services like
Wi-Fi positioning.
, 18 GPS satellites broadcast L5 signals, which are considered pre-operational prior to being broadcast by a full complement of 24 satellites in 2027.
History
The GPS project was launched in the United States in 1973 to overcome the limitations of previous navigation systems, combining ideas from several predecessors, including classified engineering design studies from the 1960s. The
U.S. Department of Defense developed the system, which originally used 24 satellites, for use by the United States military, and became fully operational in 1993. Civilian use was allowed from the 1980s.
Roger L. Easton of the
Naval Research Laboratory,
Ivan A. Getting of
The Aerospace Corporation, and
Bradford Parkinson of the
Applied Physics Laboratory are credited with inventing it.
The work of
Gladys West on the creation of the mathematical geodetic Earth model is credited as instrumental in the development of computational techniques for detecting satellite positions with the precision needed for GPS.
The design of GPS is based partly on similar ground-based
radio-navigation systems, such as
LORAN
LORAN (Long Range Navigation) was a hyperbolic navigation, hyperbolic radio navigation system developed in the United States during World War II. It was similar to the UK's Gee (navigation), Gee system but operated at lower frequencies in order ...
and the
Decca Navigator System, developed in the early 1940s. In 1955,
Friedwardt Winterberg proposed a test of
general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
—detecting time slowing in a strong gravitational field using accurate atomic clocks placed in orbit inside artificial satellites. Special and general relativity predicted that the clocks on GPS satellites, as observed by those on Earth, run 38 microseconds faster per day than those on the Earth. The design of GPS corrects for this difference; because without doing so, GPS calculated positions would accumulate errors of up to .
Predecessors
When the
Soviet Union
The Union of Soviet Socialist Republics. (USSR), commonly known as the Soviet Union, was a List of former transcontinental countries#Since 1700, transcontinental country that spanned much of Eurasia from 1922 until Dissolution of the Soviet ...
launched its first artificial satellite (
Sputnik 1
Sputnik 1 (, , ''Satellite 1''), sometimes referred to as simply Sputnik, was the first artificial Earth satellite. It was launched into an elliptical low Earth orbit by the Soviet Union on 4 October 1957 as part of the Soviet space program ...
) in 1957, two American physicists, William Guier and George Weiffenbach, at
Johns Hopkins University
The Johns Hopkins University (often abbreviated as Johns Hopkins, Hopkins, or JHU) is a private university, private research university in Baltimore, Maryland, United States. Founded in 1876 based on the European research institution model, J ...
's
Applied Physics Laboratory (APL) monitored its radio transmissions.
Within hours they realized that, because of the
Doppler effect, they could pinpoint where the satellite was along its orbit. The Director of the APL gave them access to their
UNIVAC I
The UNIVAC I (Universal Automatic Computer I) was the first general-purpose electronic digital computer design for business application produced in the United States. It was designed principally by J. Presper Eckert and John Mauchly, the invento ...
computer to perform the heavy calculations required.

Early the next year, Frank McClure, the deputy director of the APL, asked Guier and Weiffenbach to investigate the inverse problem: pinpointing the user's location, given the satellite's. (At the time, the Navy was developing the submarine-launched
Polaris
Polaris is a star in the northern circumpolar constellation of Ursa Minor. It is designated α Ursae Minoris (Latinisation of names, Latinized to ''Alpha Ursae Minoris'') and is commonly called the North Star or Pole Star. With an ...
missile, which required them to know the submarine's location.) This led them and APL to develop the
TRANSIT system. In 1959, ARPA (renamed
DARPA
The Defense Advanced Research Projects Agency (DARPA) is a research and development agency of the United States Department of Defense responsible for the development of emerging technologies for use by the military. Originally known as the Adva ...
in 1972) also played a role in TRANSIT.
TRANSIT was first successfully tested in 1960. It used a
constellation
A constellation is an area on the celestial sphere in which a group of visible stars forms Asterism (astronomy), a perceived pattern or outline, typically representing an animal, mythological subject, or inanimate object.
The first constellati ...
of five satellites and could provide a navigational fix approximately once per hour. In 1967, the U.S. Navy developed the
Timation satellite, which proved the feasibility of placing accurate clocks in space, a technology required for GPS.
In the 1970s, the ground-based
OMEGA
Omega (, ; uppercase Ω, lowercase ω; Ancient Greek ὦ, later ὦ μέγα, Modern Greek ωμέγα) is the twenty-fourth and last letter in the Greek alphabet. In the Greek numerals, Greek numeric system/isopsephy (gematria), it has a value ...
navigation system, based on phase comparison of signal transmission from pairs of stations, became the first worldwide radio navigation system. Limitations of these systems drove the need for a more universal navigation solution with greater accuracy.
Although there were wide needs for accurate navigation in military and civilian sectors, almost none of those was seen as justification for the billions of dollars it would cost in research, development, deployment, and operation of a constellation of navigation satellites. During the
Cold War
The Cold War was a period of global Geopolitics, geopolitical rivalry between the United States (US) and the Soviet Union (USSR) and their respective allies, the capitalist Western Bloc and communist Eastern Bloc, which lasted from 1947 unt ...
arms race
An arms race occurs when two or more groups compete in military superiority. It consists of a competition between two or more State (polity), states to have superior armed forces, concerning production of weapons, the growth of a military, and ...
, the nuclear threat to the existence of the United States was the one need that did justify this cost in the view of the United States Congress. This deterrent effect is why GPS was funded. It is also the reason for the ultra-secrecy at that time. The
nuclear triad consisted of the United States Navy's
submarine-launched ballistic missile
A submarine-launched ballistic missile (SLBM) is a ballistic missile capable of being launched from Ballistic missile submarine, submarines. Modern variants usually deliver multiple independently targetable reentry vehicles (MIRVs), each of which ...
s (SLBMs) along with
United States Air Force
The United States Air Force (USAF) is the Air force, air service branch of the United States Department of Defense. It is one of the six United States Armed Forces and one of the eight uniformed services of the United States. Tracing its ori ...
(USAF)
strategic bomber
A strategic bomber is a medium- to long-range Penetrator (aircraft), penetration bomber aircraft designed to drop large amounts of air-to-ground weaponry onto a distant target for the purposes of debilitating the enemy's capacity to wage war. Unl ...
s and
intercontinental ballistic missile
An intercontinental ballistic missile (ICBM) is a ballistic missile with a range (aeronautics), range greater than , primarily designed for nuclear weapons delivery (delivering one or more Thermonuclear weapon, thermonuclear warheads). Conven ...
s (ICBMs). Considered vital to the
nuclear deterrence posture, accurate determination of the SLBM launch position was a
force multiplier.
Precise navigation would enable United States
ballistic missile submarines to get an accurate fix of their positions before they launched their SLBMs. The USAF, with two-thirds of the nuclear triad, also had requirements for a more accurate and reliable navigation system. The U.S. Navy and U.S. Air Force were developing their own technologies in parallel to solve what was essentially the same problem. To increase the survivability of ICBMs, there was a proposal to use mobile launch platforms (comparable to the Soviet
SS-24 and
SS-25) and so the need to fix the launch position had similarity to the SLBM situation.
In 1960, the Air Force proposed a radio-navigation system called MOSAIC (MObile System for Accurate ICBM Control) that was essentially a 3-D LORAN System. A follow-on study, Project 57, was performed in 1963 and it was "in this study that the GPS concept was born". That same year, the concept was pursued as Project 621B, which had "many of the attributes that you now see in GPS" and promised increased accuracy for U.S. Air Force bombers as well as ICBMs.
Updates from the Navy TRANSIT system were too slow for the high speeds of Air Force operation. The
Naval Research Laboratory (NRL) continued making advances with their
Timation (Time Navigation) satellites, first launched in 1967, second launched in 1969, with the third in 1974 carrying the first
atomic clock
An atomic clock is a clock that measures time by monitoring the resonant frequency of atoms. It is based on atoms having different energy levels. Electron states in an atom are associated with different energy levels, and in transitions betwee ...
into orbit and the fourth launched in 1977.
Another important predecessor to GPS came from a different branch of the United States military. In 1964, the
United States Army
The United States Army (USA) is the primary Land warfare, land service branch of the United States Department of Defense. It is designated as the Army of the United States in the United States Constitution.Article II, section 2, clause 1 of th ...
orbited its first Sequential Collation of Range (
SECOR) satellite used for geodetic surveying. The SECOR system included three ground-based transmitters at known locations that would send signals to the satellite transponder in orbit. A fourth ground-based station, at an undetermined position, could then use those signals to fix its location precisely. The last SECOR satellite was launched in 1969.
Development
With these parallel developments in the 1960s, it was realized that a superior system could be developed by synthesizing the best technologies from 621B, Transit, Timation, and SECOR in a multi-service program. Satellite orbital position errors, induced by variations in the
gravity field and
radar refraction among others, had to be resolved. A team led by Harold L. Jury of Pan Am Aerospace Division in Florida from 1970 to 1973, used real-time data assimilation and recursive estimation to do so, reducing systematic and residual errors to a manageable level to permit accurate navigation.
During Labor Day weekend in 1973, a meeting of about twelve military officers at the Pentagon discussed the creation of a ''Defense Navigation Satellite System (DNSS)''. It was at this meeting that the real synthesis that became GPS was created. Later that year, the DNSS program was named ''Navstar.'' Navstar is often erroneously considered an acronym for "NAVigation System using Timing And Ranging" but was never considered as such by the GPS Joint Program Office (TRW may have once advocated for a different navigational system that used that acronym). With the individual satellites being associated with the name Navstar (as with the predecessors Transit and Timation), a more fully encompassing name was used to identify the constellation of Navstar satellites, ''Navstar-GPS''. Ten "
Block I" prototype satellites were launched between 1978 and 1985 (an additional unit was destroyed in a launch failure).
The effect of the ionosphere on radio transmission was investigated in a geophysics laboratory of
Air Force Cambridge Research Laboratory, renamed to Air Force Geophysical Research Lab (AFGRL) in 1974. AFGRL developed the Klobuchar model for computing
ionospheric
The ionosphere () is the ionized part of the upper atmosphere of Earth, from about to above sea level, a region that includes the thermosphere and parts of the mesosphere and exosphere. The ionosphere is ionized by solar radiation. It plays ...
corrections to GPS location. Of note is work done by Australian space scientist
Elizabeth Essex-Cohen at AFGRL in 1974. She was concerned with the curving of the paths of radio waves (
atmospheric refraction) traversing the ionosphere from NavSTAR satellites.
After
Korean Air Lines Flight 007, a
Boeing 747
The Boeing 747 is a long-range wide-body aircraft, wide-body airliner designed and manufactured by Boeing Commercial Airplanes in the United States between 1968 and 2023.
After the introduction of the Boeing 707, 707 in October 1958, Pan Am ...
carrying 269 people, was shot down by a Soviet
interceptor aircraft after straying in
prohibited airspace because of navigational errors, in the vicinity of
Sakhalin and
Moneron Islands, President
Ronald Reagan
Ronald Wilson Reagan (February 6, 1911 – June 5, 2004) was an American politician and actor who served as the 40th president of the United States from 1981 to 1989. He was a member of the Republican Party (United States), Republican Party a ...
issued a directive making GPS freely available for civilian use, once it was sufficiently developed, as a common good.
The first Block II satellite was launched on February 14, 1989, and the 24th satellite was launched in 1994. The GPS program cost at this point, not including the cost of the user equipment but including the costs of the satellite launches, has been estimated at US$5 billion (equivalent to $ billion in ).
Initially, the highest-quality signal was reserved for military use, and the signal available for civilian use was intentionally degraded, in a policy known as
Selective Availability. This changed on May 1, 2000, with U.S. President
Bill Clinton
William Jefferson Clinton (né Blythe III; born August 19, 1946) is an American politician and lawyer who was the 42nd president of the United States from 1993 to 2001. A member of the Democratic Party (United States), Democratic Party, ...
signing a policy directive to turn off Selective Availability to provide the same accuracy to civilians that was afforded to the military. The directive was proposed by the U.S. Secretary of Defense,
William Perry, in view of the widespread growth of
differential GPS
Differential Global Positioning Systems (DGPSs) supplement and enhance the positional data available from global navigation satellite systems (GNSSs). A DGPS can increase accuracy of positional data by about a thousandfold, from approximately to ...
services by private industry to improve civilian accuracy. Moreover, the U.S. military was developing technologies to deny GPS service to potential adversaries on a regional basis. Selective Availability was removed from the GPS architecture beginning with GPS-III.
Since its deployment, the U.S. has implemented several improvements to the GPS service, including new signals for civil use and increased accuracy and integrity for all users, all the while maintaining compatibility with existing GPS equipment. Modernization of the satellite system has been an ongoing initiative by the U.S. Department of Defense through a series of
satellite acquisitions to meet the growing needs of the military, civilians, and the commercial market. As of early 2015, high-quality Standard Positioning Service (SPS) GPS receivers provided horizontal accuracy of better than ,
although many factors such as receiver and antenna quality and atmospheric issues can affect this accuracy.
GPS is owned and operated by the United States government as a national resource. The Department of Defense is the steward of GPS. The ''Interagency GPS Executive Board (IGEB)'' oversaw GPS policy matters from 1996 to 2004. After that, the National Space-Based Positioning, Navigation and Timing Executive Committee was established by presidential directive in 2004 to advise and coordinate federal departments and agencies on matters concerning the GPS and related systems. The executive committee is chaired jointly by the Deputy Secretaries of Defense and Transportation. Its membership includes equivalent-level officials from the Departments of State, Commerce, and Homeland Security, the
Joint Chiefs of Staff and
NASA
The National Aeronautics and Space Administration (NASA ) is an independent agencies of the United States government, independent agency of the federal government of the United States, US federal government responsible for the United States ...
. Components of the executive office of the president participate as observers to the executive committee, and the FCC chairman participates as a liaison.
The U.S. Department of Defense is required by law to "maintain a Standard Positioning Service (as defined in the federal radio navigation plan and the standard positioning service signal specification) that will be available on a continuous, worldwide basis" and "develop measures to prevent hostile use of GPS and its augmentations without unduly disrupting or degrading civilian uses".
Timeline and modernization
* In 1972, the U.S. Air Force Central Inertial Guidance Test Facility (Holloman Air Force Base) conducted developmental flight tests of four prototype GPS receivers in a Y configuration over
White Sands Missile Range, using ground-based pseudo-satellites.
* In 1978, the first experimental Block-I GPS satellite was launched.
* In 1983, after Soviet Union interceptor aircraft shot down the civilian airliner
KAL 007 that strayed into
prohibited airspace because of navigational errors, killing all 269 people on board, U.S. President
Ronald Reagan
Ronald Wilson Reagan (February 6, 1911 – June 5, 2004) was an American politician and actor who served as the 40th president of the United States from 1981 to 1989. He was a member of the Republican Party (United States), Republican Party a ...
announced that GPS would be made available for civilian uses once it was completed,
although it had been publicly known as early as 1979, that the CA code (Coarse/Acquisition code) would be available to civilian users.
* By 1985, ten more experimental Block-I satellites had been launched to validate the concept.
* Beginning in 1988, command and control of these satellites was moved from
Onizuka AFS, California to the
2nd Satellite Control Squadron (2SCS) located at
Schriever Space Force Base in
Colorado Springs, Colorado
Colorado Springs is the most populous city in El Paso County, Colorado, United States, and its county seat. The city had a population of 478,961 at the 2020 United States census, 2020 census, a 15.02% increase since 2010 United States Census, 2 ...
.
* On February 14, 1989, the first modern Block-II satellite was launched.
* The
Gulf War
, combatant2 =
, commander1 =
, commander2 =
, strength1 = Over 950,000 soldiers3,113 tanks1,800 aircraft2,200 artillery systems
, page = https://www.govinfo.gov/content/pkg/GAOREPORTS-PEMD-96- ...
from 1990 to 1991 was the first conflict in which the military widely used GPS.
* In 1991, DARPA's project to create a miniature GPS receiver successfully ended, replacing the previous military receivers with a all-digital handheld GPS receiver.
* In 1991,
TomTom, a Dutch sat-nav manufacturer was founded.
* In 1992, the
2nd Space Wing, which originally managed the system, was inactivated and replaced by the
50th Space Wing.
* By December 1993, GPS achieved
initial operational capability (IOC), with a full constellation (24 satellites) available and providing the Standard Positioning Service (SPS).
* Full Operational Capability (FOC) was declared by
Air Force Space Command (AFSPC) in April 1995, signifying full availability of the military's secure Precise Positioning Service (PPS).
* In 1996, recognizing the importance of GPS to civilian users as well as military users, U.S. President
Bill Clinton
William Jefferson Clinton (né Blythe III; born August 19, 1946) is an American politician and lawyer who was the 42nd president of the United States from 1993 to 2001. A member of the Democratic Party (United States), Democratic Party, ...
issued a policy directive declaring GPS a
dual-use system and establishing an
Interagency GPS Executive Board to manage it as a national asset.
* In 1998, United States Vice President
Al Gore
Albert Arnold Gore Jr. (born March 31, 1948) is an American former politician, businessman, and environmentalist who served as the 45th vice president of the United States from 1993 to 2001 under President Bill Clinton. He previously served as ...
announced plans to upgrade GPS with two new civilian signals for enhanced user accuracy and reliability, particularly with respect to aviation safety, and in 2000 the
United States Congress
The United States Congress is the legislature, legislative branch of the federal government of the United States. It is a Bicameralism, bicameral legislature, including a Lower house, lower body, the United States House of Representatives, ...
authorized the effort, referring to it as ''
GPS III''.
* On May 2, 2000 "Selective Availability" was discontinued as a result of the 1996 executive order, allowing civilian users to receive a non-degraded signal globally.
* In 2004, the United States government signed an agreement with the European Community establishing cooperation related to GPS and Europe's
Galileo system.
* In 2004, United States President
George W. Bush
George Walker Bush (born July 6, 1946) is an American politician and businessman who was the 43rd president of the United States from 2001 to 2009. A member of the Bush family and the Republican Party (United States), Republican Party, he i ...
updated the national policy and replaced the executive board with the National Executive Committee for Space-Based Positioning, Navigation, and Timing.
* In November 2004,
Qualcomm
Qualcomm Incorporated () is an American multinational corporation headquartered in San Diego, California, and Delaware General Corporation Law, incorporated in Delaware. It creates semiconductors, software and services related to wireless techn ...
announced successful tests of
assisted GPS for
mobile phones.
* In 2005, the first modernized GPS satellite was launched and began transmitting a second civilian signal (L2C) for enhanced user performance.
* On September 14, 2007, the aging mainframe-based
Ground segment
A ground segment consists of all the ground-based elements of a spaceflight, space system used by operators and support personnel, as opposed to the Satellite space segment, space segment and user segment. The ground segment enables management of ...
Control System was transferred to the new Architecture Evolution Plan.
* On May 19, 2009, the United States
Government Accountability Office
The United States Government Accountability Office (GAO) is an independent, nonpartisan government agency within the legislative branch that provides auditing, evaluative, and investigative services for the United States Congress. It is the s ...
issued a report warning that some GPS satellites could fail as soon as 2010.
* On May 21, 2009, the
Air Force Space Command allayed fears of GPS failure, saying: "There's only a small risk we will not continue to exceed our performance standard."
* On January 11, 2010, an update of ground control systems caused a software incompatibility with 8,000 to 10,000 military receivers manufactured by a division of Trimble Navigation Limited of Sunnyvale, California.
* On February 25, 2010, the U.S. Air Force awarded the contract to
Raytheon Company
Raytheon is a business unit of RTX Corporation and is a major List of United States defense contractors, U.S. defense contractor and industrial corporation with manufacturing concentrations in weapons and military and commercial electronics. Fou ...
to develop the GPS Next Generation Operational Control System (OCX) to improve accuracy and availability of GPS navigation signals, and serve as a critical part of GPS modernization.
* July 24, 2020, operation of the GPS constellation is transferred to the newly established
U.S. Space Force as part of its establishment.

* On October 13, 2023, the Space Force activated
PNT Delta (Provisional) to manage US
navigation warfare assets.
2SOPS and GPS operations were realigned under this new
Delta
Delta commonly refers to:
* Delta (letter) (Δ or δ), the fourth letter of the Greek alphabet
* D (NATO phonetic alphabet: "Delta"), the fourth letter in the Latin alphabet
* River delta, at a river mouth
* Delta Air Lines, a major US carrier ...
.
Awards
On February 10, 1993, the
National Aeronautic Association selected the GPS Team as winners of the 1992
Robert J. Collier Trophy, the US's most prestigious aviation award. This team combines researchers from the Naval Research Laboratory, the U.S. Air Force, the
Aerospace Corporation,
Rockwell International Corporation, and
IBM
International Business Machines Corporation (using the trademark IBM), nicknamed Big Blue, is an American Multinational corporation, multinational technology company headquartered in Armonk, New York, and present in over 175 countries. It is ...
Federal Systems Company. The citation honors them "for the most significant development for safe and efficient navigation and surveillance of air and spacecraft since the introduction of radio navigation 50 years ago".
Two GPS developers received the
National Academy of Engineering
The National Academy of Engineering (NAE) is an American Nonprofit organization, nonprofit, NGO, non-governmental organization. It is part of the National Academies of Sciences, Engineering, and Medicine (NASEM), along with the National Academ ...
Charles Stark Draper Prize for 2003:
*
Ivan Getting, emeritus president of
The Aerospace Corporation and an engineer at
Massachusetts Institute of Technology
The Massachusetts Institute of Technology (MIT) is a Private university, private research university in Cambridge, Massachusetts, United States. Established in 1861, MIT has played a significant role in the development of many areas of moder ...
, established the basis for GPS, improving on the
World War II
World War II or the Second World War (1 September 1939 – 2 September 1945) was a World war, global conflict between two coalitions: the Allies of World War II, Allies and the Axis powers. World War II by country, Nearly all of the wo ...
land-based radio system called LORAN (''Lo''ng-range ''R''adio ''A''id to ''N''avigation).
*
Bradford Parkinson, professor of
aeronautics
Aeronautics is the science or art involved with the study, design process, design, and manufacturing of air flight-capable machines, and the techniques of operating aircraft and rockets within the atmosphere.
While the term originally referred ...
and
astronautics
Astronautics (or cosmonautics) is the practice of sending spacecraft beyond atmosphere of Earth, Earth's atmosphere into outer space. Spaceflight is one of its main applications and space science is its overarching field.
The term ''astronautics' ...
at
Stanford University
Leland Stanford Junior University, commonly referred to as Stanford University, is a Private university, private research university in Stanford, California, United States. It was founded in 1885 by railroad magnate Leland Stanford (the eighth ...
, conceived the present satellite-based system in the early 1960s and developed it in conjunction with the U.S. Air Force. Parkinson served twenty-one years in the Air Force, from 1957 to 1978, and retired with the rank of colonel.
GPS developer
Roger L. Easton received the
National Medal of Technology on February 13, 2006.
Francis X. Kane (Col. USAF, ret.) was inducted into the U.S. Air Force Space and Missile Pioneers Hall of Fame at Lackland A.F.B., San Antonio, Texas, March 2, 2010, for his role in space technology development and the engineering design concept of GPS conducted as part of Project 621B. In 1998, GPS technology was inducted into the
Space Foundation Space Technology Hall of Fame.
On October 4, 2011, the
International Astronautical Federation (IAF) awarded the Global Positioning System (GPS) its 60th Anniversary Award, nominated by IAF member, the American Institute for Aeronautics and Astronautics (AIAA). The IAF Honors and Awards Committee recognized the uniqueness of the GPS program and the exemplary role it has played in building international collaboration for the benefit of humanity. On December 6, 2018, Gladys West was inducted into the Air Force Space and Missile Pioneers Hall of Fame in recognition of her work on an extremely accurate geodetic Earth model, which was ultimately used to determine the orbit of the GPS constellation. On February 12, 2019, four founding members of the project were awarded the Queen Elizabeth Prize for Engineering with the chair of the awarding board stating: "Engineering is the foundation of civilisation; ...They've re-written, in a major way, the infrastructure of our world."
Principles
The GPS satellites carry very stable
atomic clocks
An atomic clock is a clock that measures time by monitoring the resonant frequency of atoms. It is based on atoms having different energy levels. Electron states in an atom are associated with different energy levels, and in transitions betwee ...
that are synchronized with one another and with the reference atomic clocks at the ground control stations; any drift of the clocks aboard the satellites from the reference time maintained on the ground stations is corrected regularly. Since the speed of
radio wave
Radio waves (formerly called Hertzian waves) are a type of electromagnetic radiation with the lowest frequencies and the longest wavelengths in the electromagnetic spectrum, typically with frequencies below 300 gigahertz (GHz) and wavelengths g ...
s (
speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
) is constant and independent of the satellite speed, the time delay between when the satellite transmits a signal and the ground station receives it is proportional to the distance from the satellite to the ground station. With the distance information collected from multiple ground stations, the location coordinates of any satellite at any time can be calculated with great precision.
Each GPS satellite carries an accurate record of its own position and time, and broadcasts that data continuously. Based on data received from multiple GPS
satellite
A satellite or an artificial satellite is an object, typically a spacecraft, placed into orbit around a celestial body. They have a variety of uses, including communication relay, weather forecasting, navigation ( GPS), broadcasting, scient ...
s, an end user's GPS receiver can calculate its own
four-dimensional position in
spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
; However, at a minimum, four satellites must be in view of the receiver for it to compute four unknown quantities (three position coordinates and the deviation of its own clock from satellite time).
More detailed description
Each GPS satellite continually broadcasts a signal (
carrier wave
In telecommunications, a carrier wave, carrier signal, or just carrier, is a periodic waveform (usually sinusoidal) that conveys information through a process called ''modulation''. One or more of the wave's properties, such as amplitude or freq ...
with
modulation
Signal modulation is the process of varying one or more properties of a periodic waveform in electronics and telecommunication for the purpose of transmitting information.
The process encodes information in form of the modulation or message ...
) that includes:
* A
pseudorandom code (sequence of ones and zeros) that is known to the receiver. By time-aligning a receiver-generated version and the receiver-measured version of the code, the time of arrival (TOA) of a defined point in the code sequence, called an epoch, can be found in the receiver clock time scale
* A message that includes the time of transmission (TOT) of the code epoch (in GPS time scale) and the satellite position at that time
Conceptually, the receiver measures the TOAs (according to its own clock) of four satellite signals. From the TOAs and the TOTs, the receiver forms four
time of flight (TOF) values, which are (given the speed of light) approximately equivalent to receiver-satellite ranges plus time difference between the receiver and GPS satellites multiplied by speed of light, which are called pseudo-ranges. The receiver then computes its three-dimensional position and clock deviation from the four TOFs.
In practice the receiver position (in three dimensional
Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
with origin at the Earth's center) and the offset of the receiver clock relative to the GPS time are computed simultaneously, using the
navigation equations to process the TOFs.
The receiver's Earth-centered solution location is usually converted to
latitude
In geography, latitude is a geographic coordinate system, geographic coordinate that specifies the north-south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at t ...
,
longitude
Longitude (, ) is a geographic coordinate that specifies the east- west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek lett ...
and height relative to an ellipsoidal Earth model. The height may then be further converted to height relative to the
geoid, which is essentially mean sea level. These coordinates may be displayed, such as on a
moving map display, or recorded or used by some other system, such as a vehicle guidance system.
User-satellite geometry
Although usually not formed explicitly in the receiver processing, the conceptual time differences of arrival (TDOAs) define the measurement geometry. Each TDOA corresponds to a
hyperboloid of revolution (see
Multilateration
Trilateration is the use of distances (or "ranges") for determining the unknown position coordinates of a point of interest, often around Earth ( geopositioning).
When more than three distances are involved, it may be called multilateration, f ...
). The line connecting the two satellites involved (and its extensions) forms the axis of the hyperboloid. The receiver is located at the point where three hyperboloids intersect.
It is sometimes incorrectly said that the user location is at the intersection of three spheres. While simpler to visualize, this is the case only if the receiver has a clock synchronized with the satellite clocks (i.e., the receiver measures true ranges to the satellites rather than range differences). There are marked performance benefits to the user carrying a clock synchronized with the satellites. Foremost is that only three satellites are needed to compute a position solution. If it were an essential part of the GPS concept that all users needed to carry a synchronized clock, a smaller number of satellites could be deployed, but the cost and complexity of the user equipment would increase.
Receiver in continuous operation
The description above is representative of a receiver start-up situation. Most receivers have a
track algorithm, sometimes called a ''tracker'', that combines sets of satellite measurements collected at different times—in effect, taking advantage of the fact that successive receiver positions are usually close to each other. After a set of measurements are processed, the tracker predicts the receiver location corresponding to the next set of satellite measurements. When the new measurements are collected, the receiver uses a weighting scheme to combine the new measurements with the tracker prediction. In general, a tracker can (a) improve receiver position and time accuracy, (b) reject bad measurements, and (c) estimate receiver speed and direction.
The disadvantage of a tracker is that changes in speed or direction can be computed only with a delay, and that derived direction becomes inaccurate when the distance traveled between two position measurements drops below or near the
random error
Observational error (or measurement error) is the difference between a measured value of a quantity and its unknown true value.Dodge, Y. (2003) ''The Oxford Dictionary of Statistical Terms'', OUP. Such errors are inherent in the measurement ...
of position measurement. GPS units can use measurements of the
Doppler shift
The Doppler effect (also Doppler shift) is the change in the frequency of a wave in relation to an observer who is moving relative to the source of the wave. The ''Doppler effect'' is named after the physicist Christian Doppler, who described t ...
of the signals received to compute velocity accurately. More advanced navigation systems use additional sensors like a
compass
A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself with No ...
or an
inertial navigation system
An inertial navigation system (INS; also inertial guidance system, inertial instrument) is a navigation device that uses motion sensors (accelerometers), rotation sensors (gyroscopes) and a computer to continuously calculate by dead reckoning th ...
to complement GPS.
Non-navigation applications
GPS requires four or more satellites to be visible for accurate navigation. The solution of the
navigation equations gives the position of the receiver along with the difference between the time kept by the receiver's on-board clock and the true time-of-day, thereby eliminating the need for a more precise and possibly impractical receiver based clock. Applications for GPS such as
time transfer, traffic signal timing, and
synchronization of cell phone base stations,
make use of this cheap and highly accurate timing. Some GPS applications use this time for display, or, other than for the basic position calculations, do not use it at all.
Although four satellites are required for normal operation, fewer apply in special cases. If one variable is already known, a receiver can determine its position using only three satellites. For example, a ship on the open ocean usually has a known elevation
close to 0m, and the elevation of an aircraft may be known. Some GPS receivers may use additional clues or assumptions such as reusing the last known altitude,
dead reckoning,
inertial navigation, or including information from the vehicle computer, to give a (possibly degraded) position when fewer than four satellites are visible.
[ Chapter 7]
Structure
The current GPS consists of three major segments. These are the space segment, a control segment, and a user segment.
The
U.S. Space Force develops, maintains, and operates the space and control segments. GPS satellites
broadcast signals from space, and each GPS receiver uses these signals to calculate its three-dimensional location (latitude, longitude, and altitude) and the current time.
Space segment

The space segment (SS) is composed of 24 to 32 satellites, or Space Vehicles (SV), in
medium Earth orbit
A medium Earth orbit (MEO) is an geocentric orbit, Earth-centered orbit with an altitude above a low Earth orbit (LEO) and below a high Earth orbit (HEO) – between above sea level. , and also includes the payload adapters to the boosters required to launch them into orbit. The GPS design originally called for 24 SVs, eight each in three approximately circular
orbits
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an physical body, object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an satellite, artificia ...
, but this was modified to six orbital planes with four satellites each. The six orbit planes have approximately 55°
inclination (tilt relative to the Earth's
equator
The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumferen ...
) and are separated by 60°
right ascension
Right ascension (abbreviated RA; symbol ) is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the equinox (celestial coordinates), March equinox to the (hour circle of the) point in questio ...
of the
ascending node (angle along the equator from a reference point to the orbit's intersection).
[GPS Overview from the NAVSTAR Joint Program Office](_blank)
. Retrieved December 15, 2006. The
orbital period is one-half of a
sidereal day, about 11 hours and 58 minutes, so that
the satellites pass over the same locations or almost the same locations
every day. The orbits are arranged so that at least six satellites are always within
line of sight from everywhere on the Earth's surface (see animation at right). The result of this objective is that the four satellites are not evenly spaced (90°) apart within each orbit. In general terms, the angular difference between satellites in each orbit is 30°, 105°, 120°, and 105° apart, which sum to 360°.
Orbiting at an altitude of approximately ; orbital radius of approximately , each SV makes two complete orbits each
sidereal day, repeating the same
ground track each day. This was very helpful during development because even with only four satellites, correct alignment means all four are visible from one spot for a few hours each day. For military operations, the ground track repeat can be used to ensure good coverage in combat zones.
, there are 31 satellites in the GPS
constellation
A constellation is an area on the celestial sphere in which a group of visible stars forms Asterism (astronomy), a perceived pattern or outline, typically representing an animal, mythological subject, or inanimate object.
The first constellati ...
, 27 of which are in use at a given time with the rest allocated as stand-bys. A 32nd was launched in 2018, but as of July 2019 is still in evaluation. More decommissioned satellites are in orbit and available as spares. The additional satellites improve the precision of GPS receiver calculations by providing redundant measurements. With the increased number of satellites, the constellation was changed to a nonuniform arrangement. Such an arrangement was shown to improve accuracy but also improves reliability and availability of the system, relative to a uniform system, when multiple satellites fail. With the expanded constellation, nine satellites are usually visible at any time from any point on the Earth with a clear horizon, ensuring considerable redundancy over the minimum four satellites needed for a position.
Control segment

The control segment (CS) is composed of:
# a master control station (MCS),
# an alternative master control station,
# four dedicated ground antennas, and
# six dedicated monitor stations.
The MCS can also access
Satellite Control Network (SCN) ground antennas (for additional command and control capability) and NGA (
National Geospatial-Intelligence Agency
The National Geospatial-Intelligence Agency (NGA) is a combat support agency within the United States Department of Defense whose primary mission is collecting, analyzing, and distributing geospatial intelligence (GEOINT) to support national se ...
) monitor stations. The flight paths of the satellites are tracked by dedicated U.S. Space Force monitoring stations in Hawaii,
Kwajalein Atoll
Kwajalein Atoll (; Marshallese language, Marshallese: ) is part of the Marshall Islands, Republic of the Marshall Islands (RMI). The southernmost and largest island in the atoll is named Kwajalein Island, which its majority English-speaking re ...
,
Ascension Island
Ascension Island is an isolated volcanic island, 7°56′ south of the Equator in the Atlantic Ocean, South Atlantic Ocean. It is about from the coast of Africa and from the coast of South America. It is governed as part of the British Overs ...
,
Diego Garcia
Diego Garcia is the largest island of the Chagos Archipelago. It has been used as a joint UK–U.S. military base since the 1970s, following the expulsion of the Chagossians by the UK government. The Chagos Islands are set to become a former B ...
,
Colorado Springs, Colorado
Colorado Springs is the most populous city in El Paso County, Colorado, United States, and its county seat. The city had a population of 478,961 at the 2020 United States census, 2020 census, a 15.02% increase since 2010 United States Census, 2 ...
and
Cape Canaveral, Florida, along with shared NGA monitor stations operated in England, Argentina, Ecuador, Bahrain, Australia and Washington, DC. The tracking information is sent to the MCS at
Schriever Space Force Base ESE of Colorado Springs, which is operated by the
2nd Space Operations Squadron (2 SOPS) of the U.S. Space Force. Then 2 SOPS contacts each GPS satellite regularly with a navigational update using dedicated or shared (AFSCN) ground antennas (GPS dedicated ground antennas are located at
Kwajalein,
Ascension Island
Ascension Island is an isolated volcanic island, 7°56′ south of the Equator in the Atlantic Ocean, South Atlantic Ocean. It is about from the coast of Africa and from the coast of South America. It is governed as part of the British Overs ...
,
Diego Garcia
Diego Garcia is the largest island of the Chagos Archipelago. It has been used as a joint UK–U.S. military base since the 1970s, following the expulsion of the Chagossians by the UK government. The Chagos Islands are set to become a former B ...
, and
Cape Canaveral). These updates synchronize the atomic clocks on board the satellites to within a few
nanoseconds of each other, and adjust the
ephemeris of each satellite's internal orbital model. The updates are created by a
Kalman filter
In statistics and control theory, Kalman filtering (also known as linear quadratic estimation) is an algorithm that uses a series of measurements observed over time, including statistical noise and other inaccuracies, to produce estimates of unk ...
that uses inputs from the ground monitoring stations,
space weather information, and various other inputs.
When a satellite's orbit is being adjusted, the satellite is marked ''unhealthy'', so receivers do not use it. After the maneuver, engineers track the new orbit from the ground, upload the new ephemeris, and mark the satellite healthy again. The operation control segment (OCS) currently serves as the control segment of record. It provides the operational capability that supports GPS users and keeps the GPS operational and performing within specification.
OCS replaced the 1970s-era mainframe computer at Schriever Air Force Base in September 2007. After installation, the system helped enable upgrades and provide a foundation for a new security architecture that supported U.S. armed forces.
OCS will continue to be the ground control system of record until the new segment, Next Generation GPS Operation Control System
(OCX), is fully developed and functional. The U.S. Department of Defense has claimed that the new capabilities provided by OCX will be the cornerstone for enhancing GPS's mission capabilities, enabling U.S. Space Force to enhance GPS operational services to U.S. combat forces, civil partners and domestic and international users. The GPS OCX program also will reduce cost, schedule and technical risk. It is designed to provide 50% sustainment cost savings through efficient software architecture and Performance-Based Logistics. In addition, GPS OCX is expected to cost millions of dollars less than the cost to upgrade OCS while providing four times the capability.
The GPS OCX program represents a critical part of GPS modernization and provides information assurance improvements over the current GPS OCS program.
* OCX will have the ability to control and manage GPS legacy satellites as well as the next generation of GPS III satellites, while enabling the full array of military signals.
* Built on a flexible architecture that can rapidly adapt to changing needs of GPS users allowing immediate access to GPS data and constellation status through secure, accurate and reliable information.
* Provides the warfighter with more secure, actionable and predictive information to enhance situational awareness.
* Enables new modernized signals (L1C, L2C, and L5) and has M-code capability, which the legacy system is unable to do.
* Provides significant information assurance improvements over the current program including detecting and preventing cyber attacks, while isolating, containing and operating during such attacks.
* Supports higher volume near real-time command and control capabilities and abilities.
On September 14, 2011, the U.S. Air Force announced the completion of GPS OCX Preliminary Design Review and confirmed that the OCX program is ready for the next phase of development. The GPS OCX program missed major milestones and pushed its launch into 2021, 5 years past the original deadline. According to the Government Accounting Office in 2019, the 2021 deadline looked shaky.
The project remained delayed in 2023, and was (as of June 2023) 73% over its original estimated budget. In late 2023, Frank Calvelli, the assistant secretary of the Air Force for space acquisitions and integration, stated that the project was estimated to go live some time during the summer of 2024.
User segment

The user segment (US) is composed of hundreds of thousands of U.S. and allied military users of the secure GPS Precise Positioning Service, and tens of millions of civil, commercial and scientific users of the Standard Positioning Service. In general, GPS receivers are composed of an antenna, tuned to the frequencies transmitted by the satellites, receiver-processors, and a highly stable clock (often a
crystal oscillator
A crystal oscillator is an electronic oscillator Electrical circuit, circuit that uses a piezoelectricity, piezoelectric crystal as a frequency selective surface, frequency-selective element. The oscillator frequency is often used to keep trac ...
). They may also include a display for providing location and speed information to the user.
GPS receivers may include an input for differential corrections, using the
RTCM SC-104 format. This is typically in the form of an
RS-232 port at 4,800 bit/s speed. Data is actually sent at a much lower rate, which limits the accuracy of the signal sent using RTCM. Receivers with internal DGPS receivers can outperform those using external RTCM data. , even low-cost units commonly include
Wide Area Augmentation System (WAAS) receivers.
Many GPS receivers can relay position data to a PC or other device using the
NMEA 0183
NMEA 0183 is a combined electrical and data specification for communication between marine electronics such as echo sounder, sonars, anemometer, gyrocompass, Self-steering gear, autopilot, GPS receivers and many other types of instruments. It has b ...
protocol. Although this protocol is officially defined by the National Marine Electronics Association (NMEA), references to this protocol have been compiled from public records, allowing open source tools like
gpsd to read the protocol without violating intellectual property laws. Other proprietary protocols exist as well, such as the
SiRF and
MTK protocols. Receivers can interface with other devices using methods including a serial connection,
USB
Universal Serial Bus (USB) is an industry standard, developed by USB Implementers Forum (USB-IF), for digital data transmission and power delivery between many types of electronics. It specifies the architecture, in particular the physical ...
, or
Bluetooth
Bluetooth is a short-range wireless technology standard that is used for exchanging data between fixed and mobile devices over short distances and building personal area networks (PANs). In the most widely used mode, transmission power is li ...
.
Applications
While originally a military project, GPS is considered a
dual-use technology
In politics, diplomacy and export control, dual-use items refer to goods, software and technology that can be used for both civilian and military applications. , meaning it has significant civilian applications as well.
GPS has become a widely deployed and useful tool for commerce, scientific uses, tracking, and surveillance. GPS's accurate time facilitates everyday activities such as banking, mobile phone operations, and even the control of power grids by allowing well synchronized hand-off switching.
Civilian

Many civilian applications use one or more of GPS's three basic components: absolute location, relative movement, and time transfer.
*
Amateur radio
Amateur radio, also known as ham radio, is the use of the radio frequency radio spectrum, spectrum for purposes of non-commercial exchange of messages, wireless experimentation, self-training, private recreation, radiosport, contesting, and emer ...
: clock synchronization required for several digital modes such as
FT8, FT4 and JS8; also used with
APRS for position reporting; is often critical during emergency and disaster communications support.
*
Atmosphere
An atmosphere () is a layer of gases that envelop an astronomical object, held in place by the gravity of the object. A planet retains an atmosphere when the gravity is great and the temperature of the atmosphere is low. A stellar atmosph ...
: studying the
troposphere
The troposphere is the lowest layer of the atmosphere of Earth. It contains 80% of the total mass of the Atmosphere, planetary atmosphere and 99% of the total mass of water vapor and aerosols, and is where most weather phenomena occur. From the ...
delays (recovery of the water vapor content) and
ionosphere
The ionosphere () is the ionized part of the upper atmosphere of Earth, from about to above sea level, a region that includes the thermosphere and parts of the mesosphere and exosphere. The ionosphere is ionized by solar radiation. It plays ...
delays (recovery of the number of free electrons). Recovery of Earth surface displacements due to the atmospheric pressure loading.
*
Astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
: both positional and
clock synchronization data is used in
astrometry
Astrometry is a branch of astronomy that involves precise measurements of the positions and movements of stars and other Astronomical object, celestial bodies. It provides the kinematics and physical origin of the Solar System and this galaxy, th ...
and
celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
and precise orbit determination. GPS is also used in both
amateur astronomy with
small telescopes as well as by professional observatories for finding
extrasolar planets.
*
Automated vehicle: applying precise vehicle location, coupled with
highly detailed maps, provides the context needed for cars and trucks to function without a human driver.
*
Cartography
Cartography (; from , 'papyrus, sheet of paper, map'; and , 'write') is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an imagined reality) can ...
: both civilian and military cartographers use GPS extensively.
*
Cellular telephony
Mobile telephony is the provision of wireless telephone services to mobile phones, distinguishing it from fixed-location telephony provided via landline phones. Traditionally, telephony specifically refers to voice communication, though t ...
: clock synchronization enables time transfer, which is critical for synchronizing its spreading codes with other base stations to facilitate inter-cell handoff and support hybrid GPS/cellular position detection for
mobile emergency calls and other applications. The first
handsets with integrated GPS launched in the late 1990s. The U.S.
Federal Communications Commission
The Federal Communications Commission (FCC) is an independent agency of the United States government that regulates communications by radio, television, wire, internet, wi-fi, satellite, and cable across the United States. The FCC maintains j ...
(FCC) mandated the feature in either the handset or in the towers (for use in triangulation) in 2002 so emergency services could locate 911 callers. Third-party software developers later gained access to GPS APIs from
Nextel
Nextel Communications, Inc. was an American wireless service operator that merged with and ceased to exist as a subsidiary of Sprint Corporation, which would later be bought by T-Mobile US and folded into that company. Nextel in Brazil, and form ...
upon launch, followed by
Sprint in 2006, and
Verizon
Verizon Communications Inc. ( ), is an American telecommunications company headquartered in New York City. It is the world's second-largest telecommunications company by revenue and its mobile network is the largest wireless carrier in the ...
soon thereafter.
*
Clock synchronization: the accuracy of GPS time signals (±10 ns) is second only to the atomic clocks they are based on, and is used in applications such as
GPS disciplined oscillators.
*
Disaster relief
Emergency management (also Disaster management) is a science and a system charged with creating the framework within which communities reduce vulnerability to hazards and cope with disasters. Emergency management, despite its name, does not actu ...
/
emergency services: many emergency services depend upon GPS for location and timing capabilities.
* GPS-equipped
radiosondes and
dropsondes: measure and calculate the atmospheric pressure, wind speed and direction up to from the Earth's surface.
*
Radio occultation for weather and atmospheric science applications.
*
Fleet tracking: used to identify, locate and maintain contact reports with one or more
fleet vehicles in real-time.
*
Geodesy
Geodesy or geodetics is the science of measuring and representing the Figure of the Earth, geometry, Gravity of Earth, gravity, and Earth's rotation, spatial orientation of the Earth in Relative change, temporally varying Three-dimensional spac ...
: determination of
Earth orientation parameters including the daily and sub-daily polar motion, and length-of-day variabilities, Earth's center-of-mass – geocenter motion, and low-degree gravity field parameters.
*
Geofencing:
vehicle tracking systems,
person tracking systems, and
pet tracking systems use GPS to locate devices that are attached to or carried by a person, vehicle, or pet. The application can provide continuous tracking and send notifications if the target leaves a designated (or "fenced-in") area.
*
Geotagging: applies location coordinates to digital objects such as photographs (in
Exif data) and other documents for purposes such as creating map overlays with devices like
Nikon GP-1.
*
GPS aircraft tracking
*
GPS for mining: the use of RTK GPS has significantly improved several mining operations such as drilling, shoveling, vehicle tracking, and surveying. RTK GPS provides centimeter-level positioning accuracy.
*
GPS data mining: It is possible to aggregate GPS data from multiple users to understand movement patterns, common trajectories and interesting locations. GPS data is today used in transportation and disaster engineering to forecast mobility in normal and evacuation situations (e.g., hurricanes, wildfires, earthquakes).
*
GPS tours: location determines what content to display; for instance, information about an approaching point of interest.
*
Mental health
Mental health is often mistakenly equated with the absence of mental illness. However, mental health refers to a person's overall emotional, psychological, and social well-being. It influences how individuals think, feel, and behave, and how t ...
: tracking mental health functioning and sociability.
*
Navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navig ...
: navigators value digitally precise velocity and orientation measurements, as well as precise positions in real-time with a support of orbit and clock corrections.
*
Orbit
In celestial mechanics, an orbit (also known as orbital revolution) is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an ...
determination of low-orbiting satellites with GPS receiver installed on board, such as
GOCE,
GRACE,
Jason-1,
Jason-2,
TerraSAR-X
TerraSAR-X is an imaging radar Earth observation satellite, a joint venture being carried out under a public-private-partnership between the German Aerospace Center (DLR) and Astrium, EADS Astrium. The exclusive commercial exploitation rights ar ...
,
TanDEM-X
TanDEM-X (TerraSAR-X add-on for Digital Elevation Measurement) is a German twin satellite mission using interferometric synthetic aperture radar (InSAR). It is developed in a public-private partnership between the German Aerospace centre (DLR In ...
,
CHAMP,
Sentinel-3, and some cubesats, e.g.,
CubETH.
*
Phasor measurements: GPS enables highly accurate timestamping of power system measurements, making it possible to compute
phasors.
*
Recreation
Recreation is an activity of leisure, leisure being discretionary time. The "need to do something for recreation" is an essential element of human biology and psychology. Recreational activities are often done for happiness, enjoyment, amusement, ...
: for example,
Geocaching
Geocaching (, ) is an outdoor recreational activity, in which participants use a Global Positioning System (GPS) receiver or mobile device and other navigational techniques to hide and seek containers, called ''geocaches'' or ''caches'', at sp ...
,
Geodashing
Geocaching (, ) is an outdoor recreational activity, in which participants use a Global Positioning System (GPS) receiver or mobile device and other navigational techniques to hide and seek containers, called ''geocaches'' or ''caches'', at sp ...
,
GPS drawing,
waymarking, and other kinds of
location based mobile games such as ''
Pokémon Go''.
*
Reference frames: realization and densification of the terrestrial reference frames in the framework of Global Geodetic Observing System. Co-location in space between
Satellite laser ranging
Satellite laser ranging (SLR) is a method to measure the distance to satellites in a geocentric orbit. It consists of an astronomical observatory equipped with a laser that sends ultrashort pulses of light. The pulses hit the satellite and boun ...
and microwave observations for deriving global geodetic parameters.
*
Robotics
Robotics is the interdisciplinary study and practice of the design, construction, operation, and use of robots.
Within mechanical engineering, robotics is the design and construction of the physical structures of robots, while in computer s ...
: self-navigating, autonomous robots using GPS sensors, which calculate latitude, longitude, time, speed, and heading.
* Sport: used in football and rugby for the control and analysis of the training load.
*
Surveying
Surveying or land surveying is the technique, profession, art, and science of determining the land, terrestrial Plane (mathematics), two-dimensional or Three-dimensional space#In Euclidean geometry, three-dimensional positions of Point (geom ...
: surveyors use absolute locations to make maps and determine property boundaries.
*
Tectonics
Tectonics ( via Latin ) are the processes that result in the structure and properties of the Earth's crust and its evolution through time. The field of ''planetary tectonics'' extends the concept to other planets and moons.
These processes ...
: GPS enables direct fault motion measurement of
earthquakes. Between earthquakes GPS can be used to measure
crustal motion and deformation to estimate seismic strain buildup for creating
seismic hazard maps.
*
Telematics: GPS technology integrated with computers and mobile communications technology in
automotive navigation systems.
Restrictions on civilian use
The U.S. government controls the export of some civilian receivers. All GPS receivers capable of functioning above above sea level and , or designed or modified for use with unmanned missiles and aircraft, are classified as
munitions (weapons)—which means they require
State Department
The United States Department of State (DOS), or simply the State Department, is an executive department of the U.S. federal government responsible for the country's foreign policy and relations. Equivalent to the ministry of foreign affairs o ...
export licenses. This rule applies even to otherwise purely civilian units that only receive the L1 frequency and the C/A (Coarse/Acquisition) code.
Disabling operation above these limits exempts the receiver from classification as a munition. Vendor interpretations differ. The rule refers to operation at both the target altitude and speed, but some receivers stop operating even when stationary. This has caused problems with some amateur radio balloon launches that regularly reach . These limits only apply to units or components exported from the United States. A growing trade in various components exists, including GPS units from other countries. These are expressly sold as
ITAR-free.
Military

As of 2009, military GPS applications include:
* Navigation: Soldiers use GPS to find objectives, even in the dark or in unfamiliar territory, and to coordinate troop and supply movement. In the United States armed forces, commanders use the ''Commander's Digital Assistant'' and lower ranks use the ''Soldier Digital Assistant''.
* Frequency-Hopping Radio Clock Coordination: Military radio systems using
frequency hopping modes, such as
SINCGARS and
HAVEQUICK, require all radios within a network to have the same time input to their internal clocks (+/-4 seconds in the case of SINCGARS) to be on the correct frequency at a given time. Military GPS receivers, such as the
Precision Lightweight GPS Receiver (PLGR) and
Defense Advanced GPS Receiver (DAGR), are used by
radio operators within a radio network to properly input an accurate time to said radios internal clock. More modern military radios have internal GPS receivers that synchronize the internal clock automatically.
* Target tracking: Various military weapons systems use GPS to track potential ground and air targets before flagging them as hostile. These weapon systems pass target coordinates to
precision-guided munitions to allow them to engage targets accurately. Military aircraft, particularly in
air-to-ground roles, use GPS to find targets.
* Missile and projectile guidance: GPS allows accurate targeting of various military weapons including
ICBM
An intercontinental ballistic missile (ICBM) is a ballistic missile with a range (aeronautics), range greater than , primarily designed for nuclear weapons delivery (delivering one or more Thermonuclear weapon, thermonuclear warheads). Conven ...
s,
cruise missile
A cruise missile is an unmanned self-propelled guided missile that sustains flight through aerodynamic lift for most of its flight path. Cruise missiles are designed to deliver a large payload over long distances with high precision. Modern cru ...
s,
precision-guided munitions and
artillery shell
A shell, in a modern military context, is a projectile whose payload contains an explosive, incendiary device, incendiary, or other chemical filling. Originally it was called a bombshell, but "shell" has come to be unambiguous in a military ...
s. Embedded GPS receivers able to withstand accelerations of 12,000 ''
g''
or about have been developed for use in
howitzer
The howitzer () is an artillery weapon that falls between a cannon (or field gun) and a mortar. It is capable of both low angle fire like a field gun and high angle fire like a mortar, given the distinction between low and high angle fire break ...
shells.
* Search and rescue.
* Reconnaissance: Patrol movement can be managed more closely.
* GPS satellites carry a set of nuclear detonation detectors consisting of an optical sensor called a
bhangmeter, an X-ray sensor, a dosimeter, and an electromagnetic pulse (EMP) sensor (W-sensor), that form a major portion of the
United States Nuclear Detonation Detection System. General William Shelton has stated that future satellites may drop this feature to save money.
GPS type navigation was first used in war in the
1991 Persian Gulf War, before GPS was fully developed in 1995, to assist
Coalition Forces to navigate and perform maneuvers in the war. The war also demonstrated the vulnerability of GPS to being
jammed, when Iraqi forces installed jamming devices on likely targets that emitted radio noise, disrupting reception of the weak GPS signal.
GPS's vulnerability to jamming is a threat that continues to grow as jamming equipment and experience grows. GPS signals have been reported to have been jammed many times over the years for military purposes. Russia seems to have several objectives for this approach, such as intimidating neighbors while undermining confidence in their reliance on American systems, promoting their GLONASS alternative, disrupting Western military exercises, and protecting assets from drones. China uses jamming to discourage US surveillance aircraft near the contested
Spratly Islands.
North Korea
North Korea, officially the Democratic People's Republic of Korea (DPRK), is a country in East Asia. It constitutes the northern half of the Korea, Korean Peninsula and borders China and Russia to the north at the Yalu River, Yalu (Amnok) an ...
has mounted several major jamming operations near its border with South Korea and offshore, disrupting flights, shipping and fishing operations. Iranian Armed Forces disrupted the civilian airliner plane Flight
PS752's GPS when it shot down the aircraft.
In the
Russo-Ukrainian War
The Russo-Ukrainian War began in February 2014 and is ongoing. Following Ukraine's Revolution of Dignity, Russia Russian occupation of Crimea, occupied and Annexation of Crimea by the Russian Federation, annexed Crimea from Ukraine. It then ...
, GPS-guided munitions provided to Ukraine by NATO countries experienced significant failure rates as a result of Russian electronic warfare. Excalibur artillery shells efficiency rate hitting targets dropped from 70% to 6% as Russia adapted its electronic warfare activities.
Timekeeping
Leap seconds
While most clocks derive their time from
Coordinated Universal Time
Coordinated Universal Time (UTC) is the primary time standard globally used to regulate clocks and time. It establishes a reference for the current time, forming the basis for civil time and time zones. UTC facilitates international communicat ...
(UTC), the atomic clocks on the satellites are set to ''GPS time''. The difference is that GPS time is not corrected to match the rotation of the Earth, so it does not contain new
leap seconds or other corrections that are periodically added to UTC. GPS time was set to match UTC in 1980, but has since diverged. The lack of corrections means that GPS time remains at a constant offset with
International Atomic Time (TAI) (TAI – GPS = 19 seconds). Periodic corrections are performed to the on-board clocks to keep them synchronized with ground clocks.
The GPS navigation message includes the difference between GPS time and UTC. GPS time is 18 seconds ahead of UTC because of the leap second added to UTC on December 31, 2016. Receivers subtract this offset from GPS time to calculate UTC and specific time zone values. New GPS units may not show the correct UTC time until after receiving the UTC offset message. The GPS-UTC offset field can accommodate 255 leap seconds (eight bits).
Accuracy
GPS time is theoretically accurate to about 14 nanoseconds, due to the
clock drift relative to
International Atomic Time that the atomic clocks in GPS transmitters experience. Most receivers lose some accuracy in their interpretation of the signals and are only accurate to about 100 nanoseconds.
Relativistic corrections
The GPS implements two major corrections to its time signals for relativistic effects: one for relative velocity of satellite and receiver, using the special theory of relativity, and one for the difference in gravitational potential between satellite and receiver, using general relativity. The acceleration of the satellite could also be computed independently as a correction, depending on purpose, but normally the effect is already dealt with in the first two corrections.
Format
As opposed to the year, month, and day format of the
Gregorian calendar
The Gregorian calendar is the calendar used in most parts of the world. It went into effect in October 1582 following the papal bull issued by Pope Gregory XIII, which introduced it as a modification of, and replacement for, the Julian cale ...
, the GPS date is expressed as a week number and a seconds-into-week number. The week number is transmitted as a ten-
bit field in the C/A and P(Y) navigation messages, and so it becomes zero again every 1,024 weeks (19.6 years). GPS week zero started at 00:00:00 UTC (00:00:19 TAI) on January 6, 1980, and the week number became zero again for the first time at 23:59:47 UTC on August 21, 1999 (00:00:19 TAI on August 22, 1999). It happened the second time at 23:59:42 UTC on April 6, 2019. To determine the current Gregorian date, a GPS receiver must be provided with the approximate date (to within 3,584 days) to correctly translate the GPS date signal. To address this concern in the future the modernized GPS civil navigation (CNAV) message will use a 13-bit field that only repeats every 8,192 weeks (157 years), thus lasting until 2137 (157 years after GPS week zero).
Communication
The navigational signals transmitted by GPS satellites encode a variety of information including satellite positions, the state of the internal clocks, and the health of the network. These signals are transmitted on two separate carrier frequencies that are common to all satellites in the network. Two different encodings are used: a public encoding that enables lower resolution navigation, and an encrypted encoding used by the U.S. military.
Message format
:
Each GPS satellite continuously broadcasts a ''navigation message'' on L1 (C/A and P/Y) and L2 (P/Y) frequencies at a rate of 50 bits per second (see
bitrate). Each complete message takes 750 seconds ( minutes) to complete. The message structure has a basic format of a 1500-bit-long frame made up of five subframes, each subframe being 300 bits (6 seconds) long. Subframes 4 and 5 are
subcommutated 25 times each, so that a complete data message requires the transmission of 25 full frames. Each subframe consists of ten words, each 30 bits long. Thus, with 300 bits in a subframe times 5 subframes in a frame times 25 frames in a message, each message is 37,500 bits long. At a transmission rate of 50-bit/s, this gives 750 seconds to transmit an entire
almanac message (GPS). Each 30-second frame begins precisely on the minute or half-minute as indicated by the atomic clock on each satellite.
The first subframe of each frame encodes the week number and the time within the week, as well as the data about the health of the satellite. The second and the third subframes contain the ''
ephemeris'' – the precise orbital parameters for the satellite. The fourth and fifth subframes contain the ''almanac'', which contains coarse orbit and status information for up to 32 satellites in the constellation as well as data related to error correction. Thus, to obtain an accurate satellite location from this transmitted message, the receiver must demodulate the message from each satellite it includes in its solution for 18 to 30 seconds. To collect all transmitted almanacs, the receiver must demodulate the message for 732 to 750 seconds or minutes.
All satellites broadcast at the same frequencies, encoding signals using unique
code-division multiple access
Code-division multiple access (CDMA) is a channel access method used by various radio communication technologies. CDMA is an example of channel access method, multiple access, where several transmitters can send information simultaneously over ...
(CDMA) so receivers can distinguish individual satellites from each other. The system uses two distinct CDMA encoding types: the coarse/acquisition (C/A) code, which is accessible by the general public, and the precise (P(Y)) code, which is encrypted so that only the U.S. military and other NATO nations who have been given access to the encryption code can access it.
The ephemeris is updated every 2 hours and is sufficiently stable for 4 hours, with provisions for updates every 6 hours or longer in non-nominal conditions. The almanac is updated typically every 24 hours. Additionally, data for a few weeks following is uploaded in case of transmission updates that delay data upload.
Satellite frequencies
:
All satellites broadcast at the same two frequencies, 1.57542 GHz (L1 signal) and 1.2276 GHz (L2 signal). The satellite network uses a CDMA spread-spectrum technique
where the low-bitrate message data is encoded with a high-rate
pseudo-random (PRN) sequence that is different for each satellite. The receiver must be aware of the PRN codes for each satellite to reconstruct the actual message data. The C/A code, for civilian use, transmits data at 1.023 million
chips per second, whereas the P code, for U.S. military use, transmits at 10.23 million chips per second. The actual internal reference of the satellites is 10.22999999543 MHz to compensate for
relativistic effects that make observers on the Earth perceive a different time reference with respect to the transmitters in orbit. The L1 carrier is modulated by both the C/A and P codes, while the L2 carrier is only modulated by the P code.
The P code can be encrypted as a so-called P(Y) code that is only available to military equipment with a proper decryption key. Both the C/A and P(Y) codes impart the precise time-of-day to the user.
The L3 signal at a frequency of 1.38105 GHz is used to transmit data from the satellites to ground stations. This data is used by the United States Nuclear Detonation (NUDET) Detection System (USNDS) to detect, locate, and report nuclear detonations (NUDETs) in the Earth's atmosphere and near space. One usage is the enforcement of nuclear test ban treaties.
The L4 band at 1.379913 GHz is being studied for additional ionospheric correction.
The L5 frequency band at 1.17645 GHz was added in the process of
GPS modernization. This frequency falls into an internationally protected range for aeronautical navigation, promising little or no interference under all circumstances. The first Block IIF satellite that provides this signal was launched in May 2010.
On February 5, 2016, the 12th and final Block IIF satellite was launched. The L5 consists of two carrier components that are in phase quadrature with each other. Each carrier component is bi-phase shift key (BPSK) modulated by a separate bit train. "L5, the third civil GPS signal, will eventually support safety-of-life applications for aviation and provide improved availability and accuracy."
In 2011, a conditional waiver was granted to
LightSquared to operate a terrestrial broadband service near the L1 band. Although LightSquared had applied for a license to operate in the 1525 to 1559 band as early as 2003 and it was put out for public comment, the FCC asked LightSquared to form a study group with the GPS community to test GPS receivers and identify issues that might arise due to the larger signal power from the LightSquared terrestrial network. The GPS community had not objected to the LightSquared (formerly MSV and SkyTerra) applications until November 2010, when LightSquared applied for a modification to its Ancillary Terrestrial Component (ATC) authorization. This filing (SAT-MOD-20101118-00239) amounted to a request to run several orders of magnitude more power in the same frequency band for terrestrial base stations, essentially repurposing what was supposed to be a "quiet neighborhood" for signals from space as the equivalent of a cellular network. Testing in the first half of 2011 has demonstrated that the effects from the lower 10 MHz of spectrum are minimal to GPS devices (less than 1% of the total GPS devices are affected). The upper 10 MHz intended for use by LightSquared may have some effect on GPS devices. There is some concern that this may seriously degrade the GPS signal for many consumer uses.
''
Aviation Week'' magazine reports that the latest testing (June 2011) confirms "significant jamming" of GPS by LightSquared's system.
Demodulation and decoding
Because all of the satellite signals are modulated onto the same L1 carrier frequency, the signals must be separated after demodulation. This is done by assigning each satellite a unique binary
sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is cal ...
known as a
Gold code. The signals are decoded after demodulation using addition of the Gold codes corresponding to the satellites monitored by the receiver.
If the almanac information has previously been acquired, the receiver picks the satellites to listen for by their PRNs, unique numbers in the range 1 through 32. If the almanac information is not in memory, the receiver enters a search mode until a lock is obtained on one of the satellites. To obtain a lock, it is necessary that there be an unobstructed line of sight from the receiver to the satellite. The receiver can then acquire the almanac and determine the satellites it should listen for. As it detects each satellite's signal, it identifies it by its distinct C/A code pattern. There can be a delay of up to 30 seconds before the first estimate of position because of the need to read the ephemeris data.
Processing of the navigation message enables the determination of the time of transmission and the satellite position at this time. For more information see
Demodulation and Decoding, Advanced.
Navigation equations
Problem statement
The receiver uses messages received from satellites to determine the satellite positions and time sent. The ''x, y,'' and ''z'' components of satellite position and the time sent (''s'') are designated as
'xi, yi, zi, si''where the subscript ''i'' denotes the satellite and has the value 1, 2, ..., ''n'', where ''n'' ≥ 4. When the time of message reception indicated by the on-board receiver clock is
, the true reception time is
, where ''b'' is the receiver's clock bias from the much more accurate GPS clocks employed by the satellites. The receiver clock bias is the same for all received satellite signals (assuming the satellite clocks are all perfectly synchronized). The message's transit time is
, where ''s
i'' is the satellite time. Assuming the message traveled at
the speed of light, ''c'', the distance traveled is
.
For n satellites, the equations to satisfy are:
:
where ''d
i'' is the geometric distance or range between receiver and satellite ''i'' (the values without subscripts are the ''x, y,'' and ''z'' components of receiver position):
:
Defining ''pseudoranges'' as
, we see they are biased versions of the true range:
:
.
[section 4 beginning on page 1]
Geoffrey Blewitt: Basics of the GPS Technique
Since the equations have four unknowns
'x, y, z, b''��the three components of GPS receiver position and the clock bias—signals from at least four satellites are necessary to attempt solving these equations. They can be solved by algebraic or numerical methods. Existence and uniqueness of GPS solutions are discussed by Abell and Chaffee.
When ''n'' is greater than four, this system is
overdetermined and a
fitting method must be used.
The amount of error in the results varies with the received satellites' locations in the sky, since certain configurations (when the received satellites are close together in the sky) cause larger errors. Receivers usually calculate a running estimate of the error in the calculated position. This is done by multiplying the basic resolution of the receiver by quantities called the
geometric dilution of position (GDOP) factors, calculated from the relative sky directions of the satellites used. The receiver location is expressed in a specific coordinate system, such as latitude and longitude using the
WGS 84 geodetic datum
A geodetic datum or geodetic system (also: geodetic reference datum, geodetic reference system, or geodetic reference frame, or terrestrial reference frame) is a global datum reference or reference frame for unambiguously representing the positi ...
or a country-specific system.
Geometric interpretation
The GPS equations can be solved by numerical and analytical methods. Geometrical interpretations can enhance the understanding of these solution methods.
Spheres
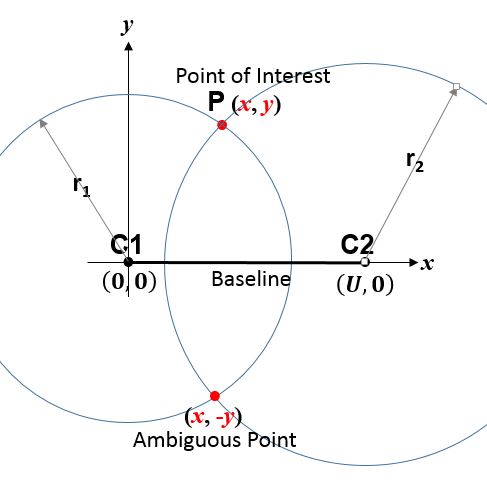
The measured ranges, called pseudoranges, contain clock errors. In a simplified idealization in which the ranges are synchronized, these true ranges represent the radii of spheres, each centered on one of the transmitting satellites. The solution for the position of the receiver is then at the intersection of the surfaces of these spheres; see
trilateration
Trilateration is the use of distances (or "ranges") for determining the unknown position coordinates of a point of interest, often around Earth ( geopositioning).
When more than three distances are involved, it may be called multilateration, f ...
(more generally, true-range multilateration). Signals from at minimum three satellites are required, and their three spheres would typically intersect at two points. One of the points is the location of the receiver, and the other moves rapidly in successive measurements and would not usually be on Earth's surface.
In practice, there are many sources of inaccuracy besides clock bias, including random errors as well as the potential for precision loss from subtracting numbers close to each other if the centers of the spheres are relatively close together. This means that the position calculated from three satellites alone is unlikely to be accurate enough. Data from more satellites can help because of the tendency for random errors to cancel out and also by giving a larger spread between the sphere centers. But at the same time, more spheres will not generally intersect at one point. Therefore, a near intersection gets computed, typically via least squares. The more signals available, the better the approximation is likely to be.
Hyperboloids

If the pseudorange between the receiver and satellite ''i'' and the pseudorange between the receiver and satellite ''j'' are subtracted, , the common receiver clock bias (''b'') cancels out, resulting in a difference of distances . The locus of points having a constant difference in distance to two points (here, two satellites) is a
hyperbola on a plane and a
hyperboloid of revolution (more specifically, a
two-sheeted hyperboloid) in 3D space (see
Multilateration
Trilateration is the use of distances (or "ranges") for determining the unknown position coordinates of a point of interest, often around Earth ( geopositioning).
When more than three distances are involved, it may be called multilateration, f ...
). Thus, from four pseudorange measurements, the receiver can be placed at the intersection of the surfaces of three hyperboloids each with
foci at a pair of satellites. With additional satellites, the multiple intersections are not necessarily unique, and a best-fitting solution is sought instead.
Inscribed sphere

The receiver position can be interpreted as the center of an
inscribed sphere
image:Circumcentre.svg, An inscribed triangle of a circle
In geometry, an inscribed plane (geometry), planar shape or solid (geometry), solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figu ...
(insphere) of radius ''bc'', given by the receiver clock bias ''b'' (scaled by the speed of light ''c''). The insphere location is such that it touches other spheres. The
circumscribing spheres are centered at the GPS satellites, whose radii equal the measured pseudoranges ''p''
i. This configuration is distinct from the one described above, in which the spheres' radii were the unbiased or geometric ranges ''d''
i.
Hypercones
The clock in the receiver is usually not of the same quality as the ones in the satellites and will not be accurately synchronized to them. This produces
pseudoranges with large differences compared to the true distances to the satellites. Therefore, in practice, the time difference between the receiver clock and the satellite time is defined as an unknown clock bias ''b''. The equations are then solved simultaneously for the receiver position and the clock bias. The solution space
'x, y, z, b''can be seen as a four-dimensional
spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
, and signals from at minimum four satellites are needed. In that case each of the equations describes a
hypercone (or spherical cone), with the cusp located at the satellite, and the base a sphere around the satellite. The receiver is at the intersection of four or more of such hypercones.
Solution methods
Least squares
When more than four satellites are available, the calculation can use the four best, or more than four simultaneously (up to all visible satellites), depending on the number of receiver channels, processing capability, and
geometric dilution of precision (GDOP).
Using more than four involves an over-determined system of equations with no unique solution; such a system can be solved by a
least-squares or weighted least squares method.
:
Iterative
Both the equations for four satellites, or the least squares equations for more than four, are non-linear and need special solution methods. A common approach is by iteration on a linearized form of the equations, such as the
Gauss–Newton algorithm.
The GPS was initially developed assuming use of a numerical least-squares solution method—i.e., before closed-form solutions were found.
Closed-form
One closed-form solution to the above set of equations was developed by S. Bancroft.
Its properties are well known;
[Chaffee, J. and Abel, J., "On the Exact Solutions of Pseudorange Equations", ''IEEE Transactions on Aerospace and Electronic Systems'', vol:30, no:4, pp: 1021–1030, 1994] in particular, proponents claim it is superior in low-
GDOP situations, compared to iterative least squares methods.
Bancroft's method is algebraic, as opposed to numerical, and can be used for four or more satellites. When four satellites are used, the key steps are inversion of a 4x4 matrix and solution of a single-variable quadratic equation. Bancroft's method provides one or two solutions for the unknown quantities. When there are two (usually the case), only one is a near-Earth sensible solution.
When a receiver uses more than four satellites for a solution, Bancroft uses the
generalized inverse
In mathematics, and in particular, algebra, a generalized inverse (or, g-inverse) of an element ''x'' is an element ''y'' that has some properties of an inverse element but not necessarily all of them. The purpose of constructing a generalized inv ...
(i.e., the pseudoinverse) to find a solution. A case has been made that iterative methods, such as the Gauss–Newton algorithm approach for solving over-determined
non-linear least squares problems, generally provide more accurate solutions.
Leick et al. (2015) states that "Bancroft's (1985) solution is a very early, if not the first, closed-form solution."
Other closed-form solutions were published afterwards,
[Alfred Kleusberg, "Analytical GPS Navigation Solution", ''University of Stuttgart Research Compendium'', 1994.][Oszczak, B., "New Algorithm for GNSS Positioning Using System of Linear Equations", ''Proceedings of the 26th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2013)'', Nashville, Tennessee, September 2013, pp. 3560–3563.] although their adoption in practice is unclear.
Error sources and analysis
GPS error analysis examines error sources in GPS results and the expected size of those errors. GPS makes corrections for receiver clock errors and other effects, but some residual errors remain uncorrected. Error sources include signal arrival time measurements, numerical calculations, atmospheric effects (ionospheric/tropospheric delays),
ephemeris and clock data, multipath signals, and natural and artificial interference. Magnitude of residual errors from these sources depends on geometric dilution of precision. Artificial errors may result from jamming devices and threaten ships and aircraft or from intentional signal degradation through selective availability, which limited accuracy to ≈ , but has been switched off since May 1, 2000.
Accuracy enhancement and surveying
Regulatory spectrum issues concerning GPS receivers
In the United States, GPS receivers are regulated under the
Federal Communications Commission
The Federal Communications Commission (FCC) is an independent agency of the United States government that regulates communications by radio, television, wire, internet, wi-fi, satellite, and cable across the United States. The FCC maintains j ...
's (FCC)
Part 15 rules. As indicated in the manuals of GPS-enabled devices sold in the United States, as a Part 15 device, it "must accept any interference received, including interference that may cause undesired operation". With respect to GPS devices in particular, the FCC states that GPS receiver manufacturers "must use receivers that reasonably discriminate against reception of signals outside their allocated spectrum".
For the last 30 years, GPS receivers have operated next to the Mobile Satellite Service band, and have discriminated against reception of mobile satellite services, such as Inmarsat, without any issue.
The spectrum allocated for GPS L1 use by the FCC is 1559 to 1610 MHz, while the spectrum allocated for satellite-to-ground use owned by Lightsquared is the Mobile Satellite Service band. Since 1996, the FCC has authorized licensed use of the spectrum neighboring the GPS band of 1525 to 1559 MHz to the
Virginia
Virginia, officially the Commonwealth of Virginia, is a U.S. state, state in the Southeastern United States, Southeastern and Mid-Atlantic (United States), Mid-Atlantic regions of the United States between the East Coast of the United States ...
company
LightSquared. On March 1, 2001, the FCC received an application from LightSquared's predecessor,
Motient
TerreStar Corporation (TSTR), formerly Motient Corp. (MNCP - 2000–2007) and ''American Mobile Satellite Corp.'' (AMSC - 1988–2000), was the controlling shareholder of ''TerreStar Networks Inc.'', ''TerreStar National Services, Inc.'' and ''Terr ...
Services, to use their allocated frequencies for an integrated satellite-terrestrial service.
In 2002, the U.S. GPS Industry Council came to an out-of-band-emissions (OOBE) agreement with LightSquared to prevent transmissions from LightSquared's ground-based stations from emitting transmissions into the neighboring GPS band of 1559 to 1610 MHz. In 2004, the FCC adopted the OOBE agreement in its authorization for LightSquared to deploy a ground-based network ancillary to their satellite system – known as the Ancillary Tower Components (ATCs) – "We will authorize MSS ATC subject to conditions that ensure that the added terrestrial component remains ancillary to the principal MSS offering. We do not intend, nor will we permit, the terrestrial component to become a stand-alone service."
This authorization was reviewed and approved by the U.S. Interdepartment Radio Advisory Committee, which includes the
U.S. Department of Agriculture, U.S. Space Force, U.S. Army,
U.S. Coast Guard,
Federal Aviation Administration
The Federal Aviation Administration (FAA) is a Federal government of the United States, U.S. federal government agency within the United States Department of Transportation, U.S. Department of Transportation that regulates civil aviation in t ...
,
National Aeronautics and Space Administration
The National Aeronautics and Space Administration (NASA ) is an independent agency of the US federal government responsible for the United States's civil space program, aeronautics research and space research. Established in 1958, it su ...
(NASA),
U.S. Department of the Interior, and
U.S. Department of Transportation.
In January 2011, the FCC conditionally authorized LightSquared's wholesale customers—such as
Best Buy,
Sharp, and
C Spire—to only purchase an integrated satellite-ground-based service from LightSquared and re-sell that integrated service on devices that are equipped to only use the ground-based signal using LightSquared's allocated frequencies of 1525 to 1559 MHz. In December 2010, GPS receiver manufacturers expressed concerns to the FCC that LightSquared's signal would interfere with GPS receiver devices
although the FCC's policy considerations leading up to the January 2011 order did not pertain to any proposed changes to the maximum number of ground-based LightSquared stations or the maximum power at which these stations could operate. The January 2011 order makes final authorization contingent upon studies of GPS interference issues carried out by a LightSquared led working group along with GPS industry and Federal agency participation. On February 14, 2012, the FCC initiated proceedings to vacate LightSquared's Conditional Waiver Order based on the NTIA's conclusion that there was currently no practical way to mitigate potential GPS interference.
GPS receiver manufacturers design GPS receivers to use spectrum beyond the GPS-allocated band. In some cases, GPS receivers are designed to use up to 400 MHz of spectrum in either direction of the L1 frequency of 1575.42 MHz, because mobile satellite services in those regions are broadcasting from space to ground, and at power levels commensurate with mobile satellite services. As regulated under the FCC's Part 15 rules, GPS receivers are not warranted protection from signals outside GPS-allocated spectrum.
This is why GPS operates next to the Mobile Satellite Service band, and also why the Mobile Satellite Service band operates next to GPS. The symbiotic relationship of spectrum allocation ensures that users of both bands are able to operate cooperatively and freely.
The FCC adopted rules in February 2003 that allowed Mobile Satellite Service (MSS) licensees such as LightSquared to construct a small number of ancillary ground-based towers in their licensed spectrum to "promote more efficient use of terrestrial wireless spectrum". In those 2003 rules, the FCC stated: "As a preliminary matter, terrestrial
ommercial Mobile Radio Service ('CMRS')and MSS ATC are expected to have different prices, coverage, product acceptance and distribution; therefore, the two services appear, at best, to be imperfect substitutes for one another that would be operating in predominantly different market segments ... MSS ATC is unlikely to compete directly with terrestrial CMRS for the same customer base...". In 2004, the FCC clarified that the ground-based towers would be ancillary, noting: "We will authorize MSS ATC subject to conditions that ensure that the added terrestrial component remains ancillary to the principal MSS offering. We do not intend, nor will we permit, the terrestrial component to become a stand-alone service."
In July 2010, the FCC stated that it expected LightSquared to use its authority to offer an integrated satellite-terrestrial service to "provide mobile broadband services similar to those provided by terrestrial mobile providers and enhance competition in the mobile broadband sector". GPS receiver manufacturers have argued that LightSquared's licensed spectrum of 1525 to 1559 MHz was never envisioned as being used for high-speed wireless broadband based on the 2003 and 2004 FCC ATC rulings making clear that the Ancillary Tower Component (ATC) would be, in fact, ancillary to the primary satellite component.
To build public support of efforts to continue the 2004 FCC authorization of LightSquared's ancillary terrestrial component vs. a simple ground-based LTE service in the Mobile Satellite Service band, GPS receiver manufacturer
Trimble Navigation Ltd. formed the "Coalition To Save Our GPS".
The FCC and LightSquared have each made public commitments to solve the GPS interference issue before the network is allowed to operate. According to Chris Dancy of the
Aircraft Owners and Pilots Association, airline pilots with the type of systems that would be affected "may go off course and not even realize it".
The problems could also affect the Federal Aviation Administration upgrade to the
air traffic control
Air traffic control (ATC) is a service provided by ground-based air traffic controllers who direct aircraft on the ground and through a given section of controlled airspace, and can provide advisory services to aircraft in non-controlled air ...
system,
United States Defense Department guidance, and local
emergency services including
911.
On February 14, 2012, the FCC moved to bar LightSquared's planned national broadband network after being informed by the
National Telecommunications and Information Administration
The National Telecommunications and Information Administration (NTIA) is a bureau of the United States Department of Commerce that serves as the president's principal adviser on telecommunications policies pertaining to the United States' ec ...
(NTIA), the federal agency that coordinates spectrum uses for the military and other federal government entities, that "there is no practical way to mitigate potential interference at this time".
[FCC press releas]
"Spokesperson Statement on NTIA Letter – LightSquared and GPS"
. February 14, 2012. Accessed March 3, 2013. LightSquared is challenging the FCC's action.
Similar systems
Following the United States's deployment of GPS, other countries have also developed their own satellite navigation systems. These systems include:
* The Russian Global Navigation Satellite System (
GLONASS
GLONASS (, ; ) is a Russian satellite navigation system operating as part of a radionavigation-satellite service. It provides an alternative to Global Positioning System (GPS) and is the second navigational system in operation with global cove ...
) was developed at the same time as GPS, but suffered from incomplete coverage of the globe until the mid-2000s. GLONASS reception in addition to GPS can be combined in a receiver thereby allowing for additional satellites available to enable faster position fixes and improved accuracy, to within . In October 2011, the full orbital constellation of 24 satellites enabled full global coverage. The GLONASS satellites' designs have undergone several upgrades, with the latest version,
GLONASS-K2, launched in 2023.
* China's
BeiDou Navigation Satellite System began global services in 2018 and finished its full deployment in 2020. It consists of satellites in three different orbits, including 24 satellites in medium-circle orbits (covering the world), 3 satellites in inclined geosynchronous orbits (covering the Asia-Pacific region), and 3 satellites in geostationary orbits (covering China).
* The
Galileo navigation satellite system, a global system being developed by the European Union and other partner countries, began operation in 2016, and has been fully deployed by 2020. In November 2018, the
FCC approved use of Galileo in the
US. As of September 2024, there are 25
launched satellites that operate in the constellation.
It is expected that the next generation of satellites will begin to become operational after 2026 to replace the first generation, which can then be used for backup capabilities.
* Japan's
Quasi-Zenith Satellite System (QZSS) is a GPS
satellite-based augmentation system to enhance GPS's accuracy in Asia-Oceania, with satellite navigation independent of GPS scheduled for 2023.
* The
Indian Regional Navigation Satellite System
Indian Regional Navigation Satellite System (IRNSS), with an operational name of NavIC (acronym for Navigation with Indian Constellation; also, 'sailor' or 'navigator' in Indian languages), is an autonomous regional satellite navigation syste ...
(Operational name 'NavIC', Navigation with Indian Constellation), deployed by India.
Backup system
In the event of adverse
space weather or the deployment of an anti-satellite weapon against GPS, the United States has no terrestrial backup system. The potential cost of such an event to the U.S. economy is estimated at $1 billion per day. The
LORAN-C system was turned off in North America in 2010 and Europe in 2015.
eLoran is proposed as an American terrestrial backup system, but as of 2024 has not received approval or funding.
China continues to operate LORAN-C transmitters,
and Russia has a similar system called
CHAYKA ("Seagull").
See also
*
List of GPS satellites
*
GPS satellite blocks
*
GPS signals
*
Satellite navigation software
*
GPS/INS
*
GPS spoofing
*
Indoor positioning system
*
Local-area augmentation system
*
Local positioning system
*
Military invention
*
Mobile phone tracking
*
Navigation paradox
*
Notice Advisory to Navstar Users
*
S-GPS
*
Geostationary balloon satellite
Notes
References
Further reading
*
*
*
*
Global Positioning System Open Courseware from
Massachusetts Institute of Technology
The Massachusetts Institute of Technology (MIT) is a Private university, private research university in Cambridge, Massachusetts, United States. Established in 1861, MIT has played a significant role in the development of many areas of moder ...
, 2012.
*
External links
FAA GPS FAQGPS.gov– General public education website created by the U.S. Government
{{Authority control
20th-century inventions
Equipment of the United States Space Force
Programs of the United States Space Force
Military equipment introduced in the 1970s
 Early the next year, Frank McClure, the deputy director of the APL, asked Guier and Weiffenbach to investigate the inverse problem: pinpointing the user's location, given the satellite's. (At the time, the Navy was developing the submarine-launched
Early the next year, Frank McClure, the deputy director of the APL, asked Guier and Weiffenbach to investigate the inverse problem: pinpointing the user's location, given the satellite's. (At the time, the Navy was developing the submarine-launched  * On October 13, 2023, the Space Force activated PNT Delta (Provisional) to manage US navigation warfare assets. 2SOPS and GPS operations were realigned under this new
* On October 13, 2023, the Space Force activated PNT Delta (Provisional) to manage US navigation warfare assets. 2SOPS and GPS operations were realigned under this new  The space segment (SS) is composed of 24 to 32 satellites, or Space Vehicles (SV), in
The space segment (SS) is composed of 24 to 32 satellites, or Space Vehicles (SV), in  The control segment (CS) is composed of:
# a master control station (MCS),
# an alternative master control station,
# four dedicated ground antennas, and
# six dedicated monitor stations.
The MCS can also access Satellite Control Network (SCN) ground antennas (for additional command and control capability) and NGA (
The control segment (CS) is composed of:
# a master control station (MCS),
# an alternative master control station,
# four dedicated ground antennas, and
# six dedicated monitor stations.
The MCS can also access Satellite Control Network (SCN) ground antennas (for additional command and control capability) and NGA ( The user segment (US) is composed of hundreds of thousands of U.S. and allied military users of the secure GPS Precise Positioning Service, and tens of millions of civil, commercial and scientific users of the Standard Positioning Service. In general, GPS receivers are composed of an antenna, tuned to the frequencies transmitted by the satellites, receiver-processors, and a highly stable clock (often a
The user segment (US) is composed of hundreds of thousands of U.S. and allied military users of the secure GPS Precise Positioning Service, and tens of millions of civil, commercial and scientific users of the Standard Positioning Service. In general, GPS receivers are composed of an antenna, tuned to the frequencies transmitted by the satellites, receiver-processors, and a highly stable clock (often a  Many civilian applications use one or more of GPS's three basic components: absolute location, relative movement, and time transfer.
*
Many civilian applications use one or more of GPS's three basic components: absolute location, relative movement, and time transfer.
*  As of 2009, military GPS applications include:
* Navigation: Soldiers use GPS to find objectives, even in the dark or in unfamiliar territory, and to coordinate troop and supply movement. In the United States armed forces, commanders use the ''Commander's Digital Assistant'' and lower ranks use the ''Soldier Digital Assistant''.
* Frequency-Hopping Radio Clock Coordination: Military radio systems using frequency hopping modes, such as SINCGARS and HAVEQUICK, require all radios within a network to have the same time input to their internal clocks (+/-4 seconds in the case of SINCGARS) to be on the correct frequency at a given time. Military GPS receivers, such as the Precision Lightweight GPS Receiver (PLGR) and Defense Advanced GPS Receiver (DAGR), are used by radio operators within a radio network to properly input an accurate time to said radios internal clock. More modern military radios have internal GPS receivers that synchronize the internal clock automatically.
* Target tracking: Various military weapons systems use GPS to track potential ground and air targets before flagging them as hostile. These weapon systems pass target coordinates to precision-guided munitions to allow them to engage targets accurately. Military aircraft, particularly in air-to-ground roles, use GPS to find targets.
* Missile and projectile guidance: GPS allows accurate targeting of various military weapons including
As of 2009, military GPS applications include:
* Navigation: Soldiers use GPS to find objectives, even in the dark or in unfamiliar territory, and to coordinate troop and supply movement. In the United States armed forces, commanders use the ''Commander's Digital Assistant'' and lower ranks use the ''Soldier Digital Assistant''.
* Frequency-Hopping Radio Clock Coordination: Military radio systems using frequency hopping modes, such as SINCGARS and HAVEQUICK, require all radios within a network to have the same time input to their internal clocks (+/-4 seconds in the case of SINCGARS) to be on the correct frequency at a given time. Military GPS receivers, such as the Precision Lightweight GPS Receiver (PLGR) and Defense Advanced GPS Receiver (DAGR), are used by radio operators within a radio network to properly input an accurate time to said radios internal clock. More modern military radios have internal GPS receivers that synchronize the internal clock automatically.
* Target tracking: Various military weapons systems use GPS to track potential ground and air targets before flagging them as hostile. These weapon systems pass target coordinates to precision-guided munitions to allow them to engage targets accurately. Military aircraft, particularly in air-to-ground roles, use GPS to find targets.
* Missile and projectile guidance: GPS allows accurate targeting of various military weapons including  The measured ranges, called pseudoranges, contain clock errors. In a simplified idealization in which the ranges are synchronized, these true ranges represent the radii of spheres, each centered on one of the transmitting satellites. The solution for the position of the receiver is then at the intersection of the surfaces of these spheres; see
The measured ranges, called pseudoranges, contain clock errors. In a simplified idealization in which the ranges are synchronized, these true ranges represent the radii of spheres, each centered on one of the transmitting satellites. The solution for the position of the receiver is then at the intersection of the surfaces of these spheres; see