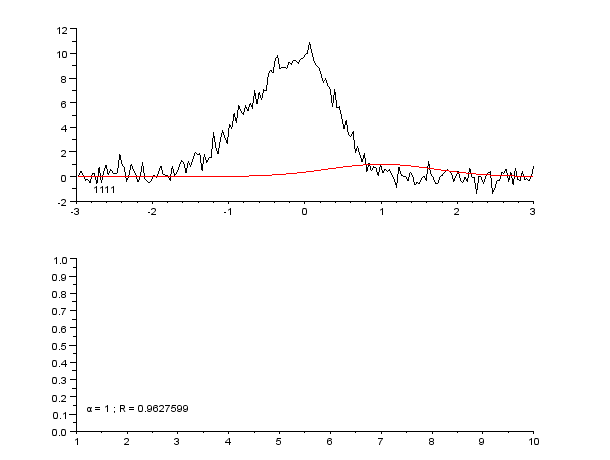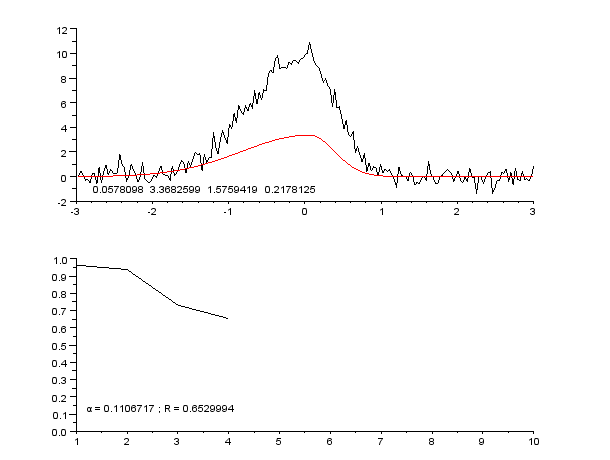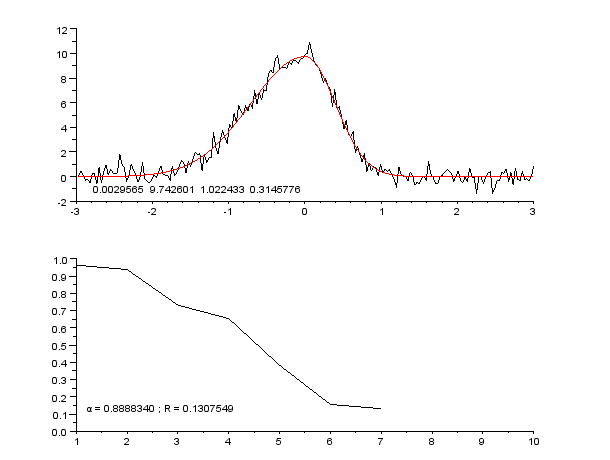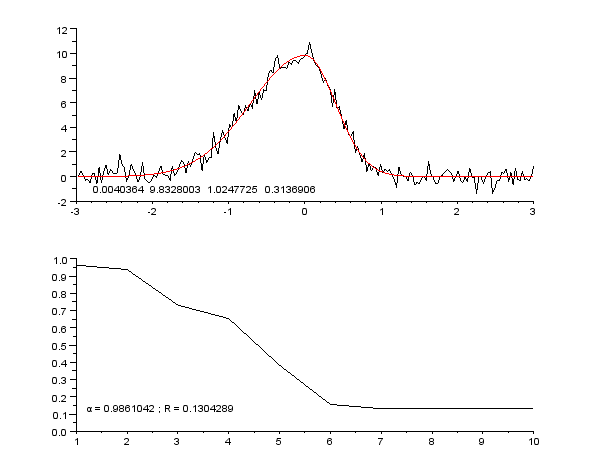
|
Gauss–Newton Algorithm
The Gauss–Newton algorithm is used to solve non-linear least squares problems, which is equivalent to minimizing a sum of squared function values. It is an extension of Newton's method for finding a minimum of a non-linear function. Since a sum of squares must be nonnegative, the algorithm can be viewed as using Newton's method to iteratively approximate zeroes of the components of the sum, and thus minimizing the sum. In this sense, the algorithm is also an effective method for solving overdetermined systems of equations. It has the advantage that second derivatives, which can be challenging to compute, are not required. Non-linear least squares problems arise, for instance, in non-linear regression, where parameters in a model are sought such that the model is in good agreement with available observations. The method is named after the mathematicians Carl Friedrich Gauss and Isaac Newton, and first appeared in Gauss's 1809 work ''Theoria motus corporum coelestium in sec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overdetermined System
In mathematics, a system of equations is considered overdetermined if there are more equations than unknowns. An overdetermined system is almost always inconsistent equations, inconsistent (it has no solution) when constructed with random coefficients. However, an overdetermined system will have solutions in some cases, for example if some equation occurs several times in the system, or if some equations are linear combinations of the others. The terminology can be described in terms of the concept of constraint counting. Each Variable (mathematics), unknown can be seen as an available degree of freedom. Each equation introduced into the system can be viewed as a constraint (mathematics), constraint that restricts one degree of freedom. Therefore, the critical case occurs when the number of equations and the number of free variables are equal. For every variable giving a degree of freedom, there exists a corresponding constraint. The ''overdetermined'' case occurs when the syste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regression Pic Assymetrique
Regression or regressions may refer to: Arts and entertainment * ''Regression'' (film), a 2015 horror film by Alejandro Amenábar, starring Ethan Hawke and Emma Watson * ''Regression'' (magazine), an Australian punk rock fanzine (1982–1984) * ''Regressions'' (album), 2010 album by Cleric Computing * Software regression, the appearance of a bug in functionality that was working correctly in a previous revision ** Regression testing, a software testing method which seeks to uncover regression bugs Hypnosis * Age regression in therapy, a process claiming to retrieve memories * Past life regression, a process claiming to retrieve memories of previous lives Science * Marine regression, coastal advance due to falling sea level, the opposite of marine transgression * Regression (medicine), a characteristic of diseases to express lighter symptoms or less extent (mainly for tumors), without disappearing totally * Regression (psychology), a defensive reaction to some unaccepted i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ill-conditioned
In numerical analysis, the condition number of a function measures how much the output value of the function can change for a small change in the input argument. This is used to measure how sensitive a function is to changes or errors in the input, and how much error in the output results from an error in the input. Very frequently, one is solving the inverse problem: given f(x) = y, one is solving for ''x,'' and thus the condition number of the (local) inverse must be used. The condition number is derived from the theory of propagation of uncertainty, and is formally defined as the value of the asymptotic worst-case relative change in output for a relative change in input. The "function" is the solution of a problem and the "arguments" are the data in the problem. The condition number is frequently applied to questions in linear algebra, in which case the derivative is straightforward but the error could be in many different directions, and is thus computed from the geometry of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rate Of Convergence
In mathematical analysis, particularly numerical analysis, the rate of convergence and order of convergence of a sequence that converges to a limit are any of several characterizations of how quickly that sequence approaches its limit. These are broadly divided into rates and orders of convergence that describe how quickly a sequence further approaches its limit once it is already close to it, called asymptotic rates and orders of convergence, and those that describe how quickly sequences approach their limits from starting points that are not necessarily close to their limits, called non-asymptotic rates and orders of convergence. Asymptotic behavior is particularly useful for deciding when to stop a sequence of numerical computations, for instance once a target precision has been reached with an iterative root-finding algorithm, but pre-asymptotic behavior is often crucial for determining whether to begin a sequence of computations at all, since it may be impossible or imprac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Convergence
In numerical analysis, an iterative method is called locally convergent if the successive approximations produced by the method are guaranteed to converge to a solution when the initial approximation is already close enough to the solution. Iterative methods for nonlinear equations and their systems, such as Newton's method are usually only locally convergent. An iterative method that converges for an arbitrary initial approximation is called globally convergent. Iterative methods for systems of linear equations In mathematics, a linear equation is an equation that may be put in the form a_1x_1+\ldots+a_nx_n+b=0, where x_1,\ldots,x_n are the variables (or unknowns), and b,a_1,\ldots,a_n are the coefficients, which are often real numbers. The coefficie ... are usually globally convergent. Numerical analysis Iterative methods Optimization algorithms and methods {{mathanalysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of a function, graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" increasing or decreasing (hence the name). For a differentiable function of several real variables, a stationary point is a point on the surface (mathematics), surface of the graph where all its partial derivatives are zero (equivalently, the gradient has zero vector norm, norm). The notion of stationary points of a real-valued function is generalized as ''Critical point (mathematics), critical points'' for complex-valued functions. Stationary points are easy to visualize on the graph of a function of one variable: they correspond to the points on the graph where the tangent is horizontal (i.e., Parallel (geometry), parallel to the Abscissa, -axis). For a function of two variables, they correspond to the points on the gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descent Direction
In optimization, a descent direction is a vector \mathbf\in\mathbb R^n that points towards a local minimum \mathbf^* of an objective function f:\mathbb R^n\to\mathbb R. Computing \mathbf^* by an iterative method, such as line search defines a descent direction \mathbf_k\in\mathbb R^n at the kth iterate to be any \mathbf_k such that \langle\mathbf_k,\nabla f(\mathbf_k)\rangle < 0, where denotes the . The motivation for such an approach is that small steps along guarantee that is reduced, by . Using this definition, the negative of a non-zero gradient is always a descent direction, as |
Gauss Newton Illustration
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, Geodesy, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and professor of astronomy from 1807 until his death in 1855. While studying at the University of Göttingen, he propounded several mathematical theorems. As an independent scholar, he wrote the masterpieces ''Disquisitiones Arithmeticae'' and ''Theoria motus corporum coelestium''. Gauss produced the second and third complete proofs of the fundamental theorem of algebra. In number theory, he made numerous contributions, such as the Gauss composition law, composition law, the Quadratic reciprocity, law of quadratic reciprocity and the Fermat polygonal number theorem. He also contributed to the theory of binary and ternary quadratic forms, the construction of the heptadecagon, and the theory of Hypergeometric function, hypergeometric ser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Gradient
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-semidefinite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
QR Factorization
In linear algebra, a QR decomposition, also known as a QR factorization or QU factorization, is a decomposition of a matrix ''A'' into a product ''A'' = ''QR'' of an orthonormal matrix ''Q'' and an upper triangular matrix ''R''. QR decomposition is often used to solve the linear least squares (LLS) problem and is the basis for a particular eigenvalue algorithm, the QR algorithm. Cases and definitions Square matrix Any real square matrix ''A'' may be decomposed as : A = QR, where ''Q'' is an orthogonal matrix (its columns are orthogonal unit vectors meaning and ''R'' is an upper triangular matrix (also called right triangular matrix). If ''A'' is invertible, then the factorization is unique if we require the diagonal elements of ''R'' to be positive. If instead ''A'' is a complex square matrix, then there is a decomposition ''A'' = ''QR'' where ''Q'' is a unitary matrix (so the conjugate transpose If ''A'' has ''n'' linearly independent columns, then the first ''n'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cholesky Decomposition
In linear algebra, the Cholesky decomposition or Cholesky factorization (pronounced ) is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful for efficient numerical solutions, e.g., Monte Carlo simulations. It was discovered by André-Louis Cholesky for real matrices, and posthumously published in 1924. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations. Statement The Cholesky decomposition of a Hermitian positive-definite matrix , is a decomposition of the form \mathbf = \mathbf^, where is a lower triangular matrix with real and positive diagonal entries, and * denotes the conjugate transpose of . Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition. The converse holds trivially: if can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |