|
Multilateration
Trilateration is the use of distances (or "ranges") for determining the unknown position coordinates of a point of interest, often around Earth ( geopositioning). When more than three distances are involved, it may be called multilateration, for emphasis. The distances or ranges might be ordinary Euclidean distances ( slant ranges) or spherical distances (scaled central angles), as in '' true-range multilateration''; or biased distances ( pseudo-ranges), as in '' pseudo-range multilateration''. Trilateration or multilateration should not be confused with '' triangulation'', which uses angles for positioning; and '' direction finding'', which determines the line of sight direction to a target without determining the radial distance. Terminology Multiple, sometimes overlapping and conflicting terms are employed for similar concepts – e.g., ''multilateration'' without modification has been used for aviation systems employing both true-ranges and pseudo-ranges."Multilatera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudo-range Multilateration
Pseudo-range multilateration, often simply multilateration (MLAT) when in context, is a technique for geopositioning, determining the position of an unknown point, such as a vehicle, based on measurement of biased ''time of flight, times of flight'' (TOFs) of energy waves traveling between the vehicle and multiple stations at known locations. TOFs are biased by synchronization errors in the difference between ''time of arrival, times of arrival'' (TOA) and ''time of transmission, times of transmission'' (TOT): ''TOF=TOA-TOT''. ''Pseudo-ranges'' (PRs) are TOFs multiplied by the wave propagation speed: ''PRTOFs''. In general, the stations' clocks are assumed synchronized but the vehicle's clock is desynchronized. In MLAT for surveillance, the waves are transmitted by the vehicle and received by the stations; the TOT is unique and unknown, while the TOAs are multiple and known. When MLAT is used for navigation (as in ''hyperbolic navigation''), the waves are transmitted by the sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
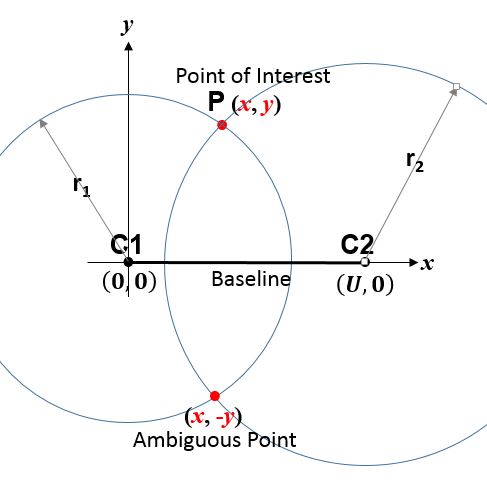
True-range Multilateration
True-range multilateration (also termed range-range multilateration and spherical multilateration) is a method to determine the location of a movable vehicle or stationary point in space using multiple ranging, ranges (distances) between the vehicle/point and multiple spatially-separated known locations (often termed "stations"). ''Accuracy limitations of range-range (spherical) multilateration systems'' Harry B. Lee, Massachusetts Institute of Technology, Lincoln Laboratory, Report Number: DOT/TSC-RA-3-8-(1) (Technical note 1973-43), Oct. 11, 1973 Energy waves may be involved in determining range, but are not required. True-range multilateration is both a mathematical topic and an applied technique used in several fields. A practical application involving a fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudo-range
The pseudorange (from pseudo- and range) is the ''pseudo'' distance between a satellite and a navigation satellite receiver (see GNSS positioning calculation), for instance Global Positioning System (GPS) receivers. To determine its position, a satellite navigation receiver will determine the ranges to (at least) four satellites as well as their positions at time of transmitting. Knowing the satellites' orbital parameters, these positions can be calculated for any point in time. The pseudoranges of each satellite are obtained by multiplying the speed of light by the time the signal has taken from the satellite to the receiver. As there are accuracy errors in the time measured, the term ''pseudo''-ranges is used rather than ranges for such distances. Pseudorange and time error estimation Typically a quartz oscillator is used in the receiver to do the timing. The accuracy of quartz clocks in general is worse (i.e. more) than one part in a million; thus, if the clock hasn't been co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geopositioning
Geopositioning is the process of determining or estimating the geographic position of an object or a person. Geopositioning yields a set of geographic coordinates (such as latitude and longitude) in a given map datum. Geographic positions may also be expressed indirectly, as a distance in linear referencing or as a bearing and range from a known landmark. In turn, positions can determine a meaningful location, such as a street address. Geoposition is sometimes referred to as ''geolocation'', and the process of geopositioning may also be described as ''geo-localization''. Specific instances include: * animal geotracking, the process of inferring the location of animals over time; * positioning system, the mechanisms for the determination of geographic positions in general; * internet geolocation, geolocating a device connected to the internet; * and mobile phone tracking. Geofencing ''Geofencing'' involves creating a virtual geographic boundary (a geofence), enabling software ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the ''base'', in which case the opposite vertex is called the ''apex''; the shortest segment between the base and apex is the ''height''. The area of a triangle equals one-half the product of height and base length. In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the center (geometry), ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is spherical Earth, often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Coordinate System
In mathematics, the polar coordinate system specifies a given point in a plane by using a distance and an angle as its two coordinates. These are *the point's distance from a reference point called the ''pole'', and *the point's direction from the pole relative to the direction of the ''polar axis'', a ray drawn from the pole. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. The pole is analogous to the origin in a Cartesian coordinate system. Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more intuitive to model using polar coordinates. The polar coordinate system i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direction (geometry)
In geometry, direction, also known as spatial direction or vector direction, is the common characteristic of all rays which coincide when translated to share a common endpoint; equivalently, it is the common characteristic of vectors (such as the relative position between a pair of points) which can be made equal by scaling (by some positive scalar multiplier). Two vectors sharing the same direction are said to be ''codirectional'' or ''equidirectional''. All co directional line segments sharing the same size (length) are said to be '' equipollent''. Two equipollent segments are not necessarily coincident; for example, a given direction can be evaluated at different starting positions, defining different unit directed line segments (as a bound vector instead of a free vector). A direction is often represented as a unit vector, the result of dividing a vector by its length. A direction can alternately be represented by a point on a circle or sphere, the intersection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Direction Finding
Direction finding (DF), radio direction finding (RDF), or radiogoniometry is the use of radio waves to determine the direction to a radio source. The source may be a cooperating radio transmitter or may be an inadvertent source, a naturally-occurring radio source, or an illicit or enemy system. Radio direction finding differs from radar in that only the direction is determined by any one receiver; a radar system usually also gives a distance to the object of interest, as well as direction. By triangulation, the location of a radio source can be determined by measuring its direction from two or more locations. Radio direction finding is used in radio navigation for ships and aircraft, to locate emergency transmitters for search and rescue, for tracking wildlife, and to locate illegal or interfering transmitters. During the Second World War, radio direction finding was used by both sides to locate and direct aircraft, surface ships, and submarines. RDF systems can be used w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude (mathematics), magnitude or Physical quantity, quantity of these types of geometric figures and in this context an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |