|
Hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Hyperbolas arise in many ways: * as the curve representing the reciprocal function y(x) = 1/x in the Cartesian plane, * as the path followed by the shadow of the tip of a sundial, * as the shape of an open orbit (as distinct from a closed elliptical orbit), such as the orbit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola (PSF)
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Hyperbolas arise in many ways: * as the curve representing the reciprocal function y(x) = 1/x in the Cartesian plane, * as the path followed by the shadow of the tip of a sundial, * as the shape of an open orbit (as distinct from a closed elliptical orbit), such as the orbit o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
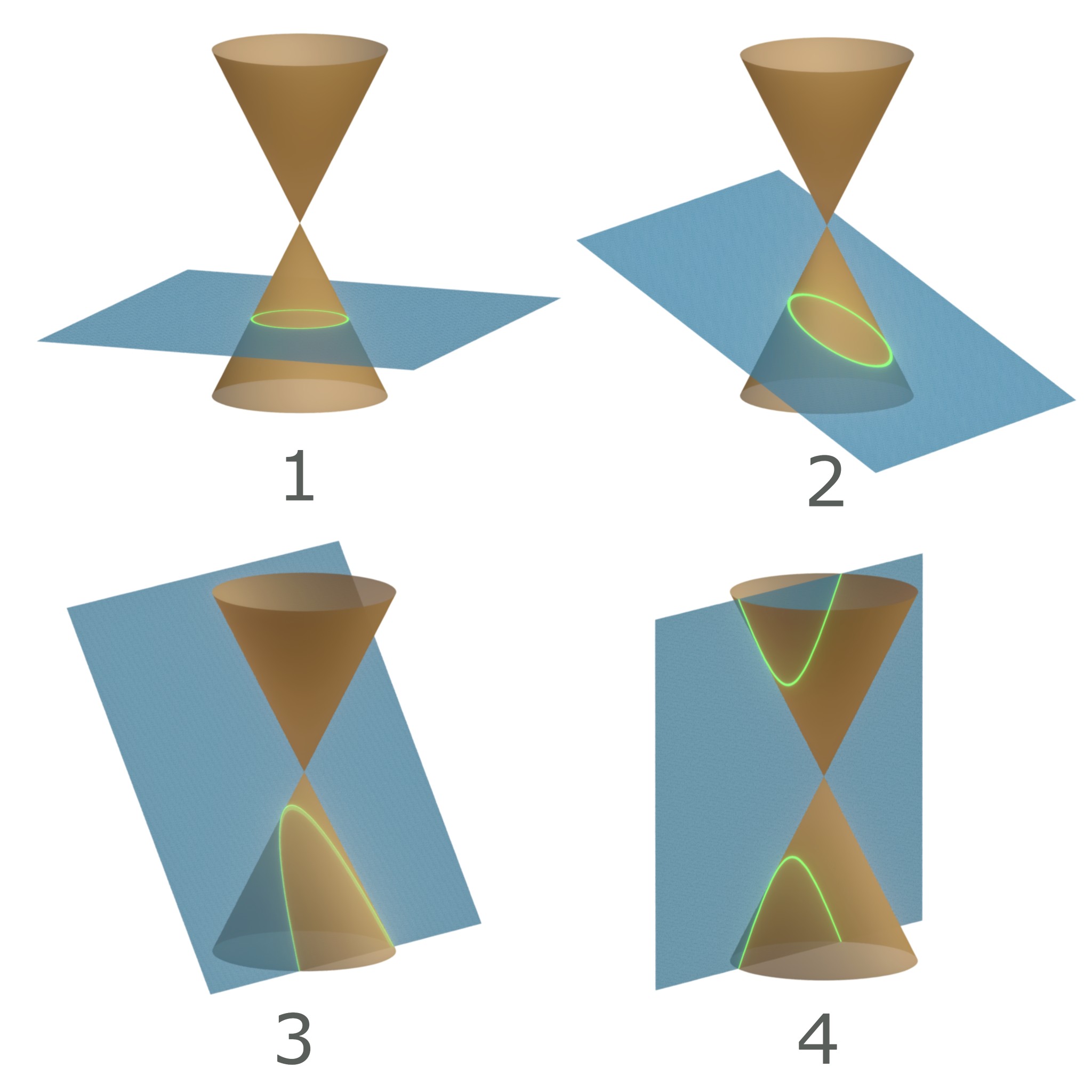
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a '' focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the '' eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directrix (conic Section)
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the Conical surface, surface of a cone (geometry), cone with a plane (mathematics), plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The Greek mathematics, ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set (mathematics), set of those points whose distances to some particular point, called a ''Focus (geometry), focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''Eccentricity (mathematics), eccentricity''. The t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane Curve
In mathematics, a plane curve is a curve in a plane that may be either a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases are smooth plane curves (including piecewise smooth plane curves), and algebraic plane curves. Plane curves also include the Jordan curves (curves that enclose a region of the plane but need not be smooth) and the graphs of continuous functions. Symbolic representation A plane curve can often be represented in Cartesian coordinates by an implicit equation of the form f(x,y)=0 for some specific function ''f''. If this equation can be solved explicitly for ''y'' or ''x'' – that is, rewritten as y=g(x) or x=h(y) for specific function ''g'' or ''h'' – then this provides an alternative, explicit, form of the representation. A plane curve can also often be represented in Cartesian coordinates by a parametric equation of the form (x,y)=(x(t), y(t)) for specific functions x(t) and y(t). Plane curves can sometimes also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eccentricity (mathematics)
In mathematics, the eccentricity of a conic section is a non-negative real number that uniquely characterizes its shape. More formally two conic sections are similar if and only if they have the same eccentricity. One can think of the eccentricity as a measure of how much a conic section deviates from being circular. In particular: * The eccentricity of a circle is zero. * The eccentricity of an ellipse which is not a circle is greater than zero but less than 1. * The eccentricity of a parabola is 1. * The eccentricity of a hyperbola is greater than 1. * The eccentricity of a pair of lines is \infty Definitions Any conic section can be defined as the locus of points whose distances to a point (the focus) and a line (the directrix) are in a constant ratio. That ratio is called the eccentricity, commonly denoted as . The eccentricity can also be defined in terms of the intersection of a plane and a double-napped cone associated with the conic section. If the cone is orie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptote
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity. The word asymptote is derived from the Greek ἀσύμπτωτος (''asumptōtos'') which means "not falling together", from ἀ priv. + σύν "together" + πτωτ-ός "fallen". The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve. There are three kinds of asymptotes: ''horizontal'', ''vertical'' and ''oblique''. For curves given by the graph of a function , horizontal asymptotes are horizontal lines that the graph of the function approaches as ''x'' tends to Vertical asymptotes are vertical lines near which t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an involution). Multiplying by a number is the same as dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yields the original number (since the product of the number and its reciprocal is 1). The term ''reciprocal' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focus (geometry)
In geometry, focuses or foci (), singular focus, are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an ''n''-ellipse. Conic sections Defining conics in terms of two foci An ellipse can be defined as the locus of points for which the sum of the distances to two given foci is constant. A circle is the special case of an ellipse in which the two foci coincide with each other. Thus, a circle can be more simply defined as the locus of points each of which is a fixed distance from a single given focus. A circle can also be defined as the circle of Apollonius, in terms of two different foci, as the locus of points having a fixed ratio of distances to the two foci. A parabola ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Navigation
Hyperbolic navigation is a class of radio navigation systems in which a navigation receiver instrument is used to determine location based on the difference in timing ( phase) of radio waves received from radio navigation beacon transmitters. Such systems rely on the ability of two widely separated stations to broadcast a signal that is highly correlated in time. Typical systems either broadcast short pulses at the same time, or continual signals that are identical in phase. A receiver located at the midpoint between the two stations will receive the signals at the same time or have identical phase, but at any other location the signal from the closer station will be received first or have a different phase. Determining the location of a receiver requires that the two synchronized stations be tuned in at the same time so the signals can be compared. This reveals a ''difference'' in time, corresponding to a relative distance closer to one station or the other. Plotting all the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Axes
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetry
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation, reflection, rotation or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article. Mathematical symmetry may be observed with respect to the passage of time; as a spatial relationship; through geometric transformations; through other kinds of functional transformations; and as an aspect of abstract objects, including theoretic models, language, and music. This article describes symmetry from three perspectives: in mathematics, including geometry, the most familiar type of symmetry for many people; in science and n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spacecraft
A spacecraft is a vehicle or machine designed to spaceflight, fly in outer space. A type of artificial satellite, spacecraft are used for a variety of purposes, including Telecommunications, communications, Earth observation satellite, Earth observation, Weather satellite, meteorology, navigation, space colonization, Planetary science, planetary exploration, and Space transport, transportation of Human spaceflight, humans and cargo spacecraft, cargo. All spacecraft except single-stage-to-orbit vehicles cannot get into space on their own, and require a launch vehicle (carrier rocket). On a sub-orbital spaceflight, a space vehicle enters outer space, space and then returns to the surface without having gained sufficient energy or velocity to make a full Earth orbit. For orbital spaceflights, spacecraft enter closed orbits around the Earth or around other Astronomical object, celestial bodies. Spacecraft used for human spaceflight carry people on board as crew or passengers from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |