Dispersion (optics) on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 Material dispersion can be a desirable or undesirable effect in optical applications. The dispersion of light by glass prisms is used to construct
Material dispersion can be a desirable or undesirable effect in optical applications. The dispersion of light by glass prisms is used to construct
 Beyond simply describing a change in the phase velocity over wavelength, a more serious consequence of dispersion in many applications is termed
Beyond simply describing a change in the phase velocity over wavelength, a more serious consequence of dispersion in many applications is termed
Dispersive Wiki
– discussing the mathematical aspects of dispersion.
– Encyclopedia of Laser Physics and Technology
Animations demonstrating optical dispersion
by QED
Interactive webdemo for chromatic dispersion
Institute of Telecommunications, University of Stuttgart {{Authority control Glass physics Optics
 In
In optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviole ...
, and by analogy other branches of physics dealing with wave propagation
Wave propagation is any of the ways in which waves travel. Single wave propagation can be calculated by 2nd order wave equation ( standing wavefield) or 1st order one-way wave equation.
With respect to the direction of the oscillation relative to ...
, dispersion is the phenomenon in which the phase velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, ...
of a wave
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (res ...
depends on its frequency; sometimes the term chromatic dispersion is used for specificity to optics in particular.
A medium having this common property may be termed a dispersive medium (plural ''dispersive media'').
Although the term is used in the field of optics to describe light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 tera ...
and other electromagnetic wave
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy. It includes radio waves, microwaves, infrared, (visib ...
s, dispersion in the same sense can apply to any sort of wave motion such as acoustic dispersion Acoustic dispersion is the phenomenon of a sound wave separating into its component frequencies as it passes through a material. The phase velocity of the sound wave is viewed as a function of frequency. Hence, separation of component frequencies ...
in the case of sound and seismic waves, and in gravity wave
In fluid dynamics, gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere ...
s (ocean waves). Within optics, dispersion is a property of telecommunication signals along transmission line
In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmis ...
s (such as microwaves
Microwave is a form of electromagnetic radiation with wavelengths ranging from about one meter to one millimeter corresponding to frequencies between 300 MHz and 300 GHz respectively. Different sources define different frequency rang ...
in coaxial cable
Coaxial cable, or coax (pronounced ) is a type of electrical cable consisting of an inner conductor surrounded by a concentric conducting shield, with the two separated by a dielectric ( insulating material); many coaxial cables also have a p ...
) or the pulses of light in optical fiber
An optical fiber, or optical fibre in Commonwealth English, is a flexible, transparent fiber made by drawing glass (silica) or plastic to a diameter slightly thicker than that of a human hair. Optical fibers are used most often as a means to ...
. Physically, dispersion translates in a loss of kinetic energy through absorption.
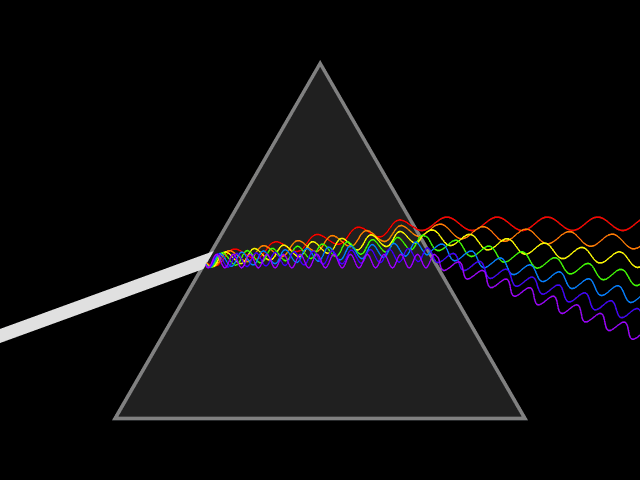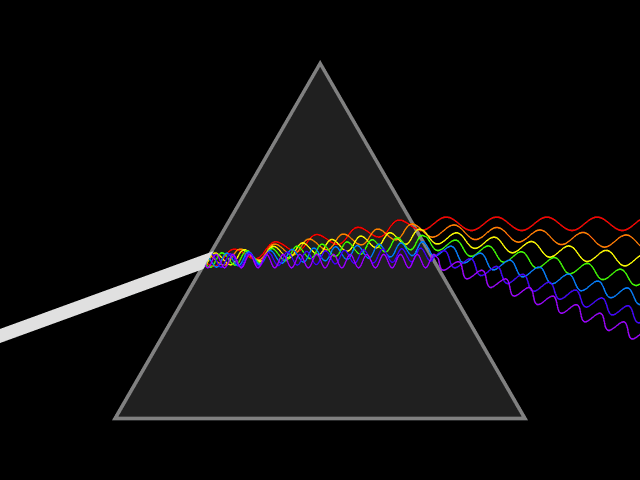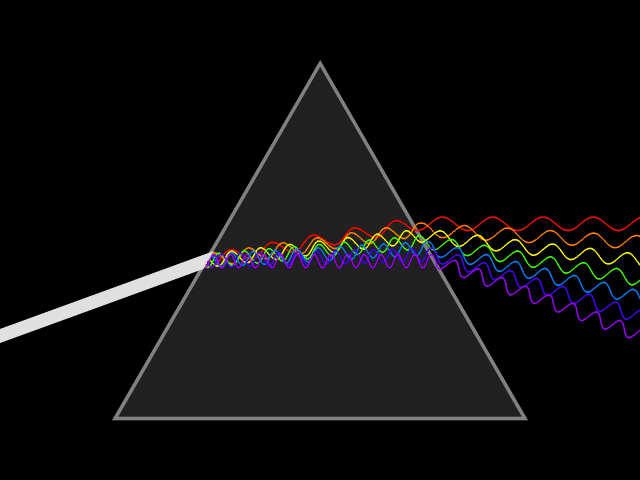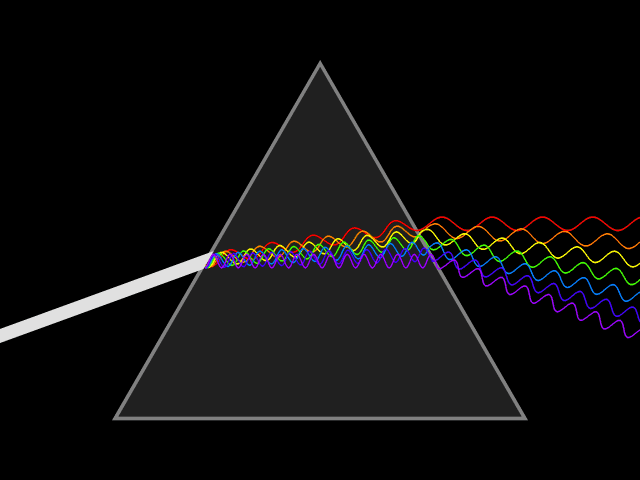
In optics, one important and familiar consequence of dispersion is the change in the angle of refraction
In physics, refraction is the redirection of a wave as it passes from one medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commonly observed phenomeno ...
of different colors of light, as seen in the spectrum produced by a dispersive prism
Prism usually refers to:
* Prism (optics), a transparent optical component with flat surfaces that refract light
* Prism (geometry), a kind of polyhedron
Prism may also refer to:
Science and mathematics
* Prism (geology), a type of sedimentary ...
and in chromatic aberration
In optics, chromatic aberration (CA), also called chromatic distortion and spherochromatism, is a failure of a lens to focus all colors to the same point. It is caused by dispersion: the refractive index of the lens elements varies with the wave ...
of lenses. Design of compound achromatic lens
An achromatic lens or achromat is a lens that is designed to limit the effects of chromatic and spherical aberration. Achromatic lenses are corrected to bring two wavelengths (typically red and blue) into focus on the same plane.
The most comm ...
es, in which chromatic aberration is largely cancelled, uses a quantification of a glass's dispersion given by its Abbe number
In optics and lens design, the Abbe number, also known as the V-number or constringence of a transparent material, is an approximate measure of the material's dispersion (change of refractive index versus wavelength), with high values of ''V'' in ...
''V'', where ''lower'' Abbe numbers correspond to ''greater'' dispersion over the visible spectrum
The visible spectrum is the portion of the electromagnetic spectrum that is visual perception, visible to the human eye. Electromagnetic radiation in this range of wavelengths is called ''visible light'' or simply light. A typical human eye wil ...
. In some applications such as telecommunications, the absolute phase of a wave is often not important but only the propagation of wave packet
In physics, a wave packet (or wave train) is a short "burst" or "envelope" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of diff ...
s or "pulses"; in that case one is interested only in variations of group velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope'' of the wave—propagates through space.
For example, if a stone is thrown into the middl ...
with frequency, so-called group-velocity dispersion.
All common transmission media
A transmission medium is a system or substance that can mediate the propagation of signals for the purposes of telecommunication. Signals are typically imposed on a wave of some kind suitable for the chosen medium. For example, data can modulate ...
also vary in attenuation
In physics, attenuation (in some contexts, extinction) is the gradual loss of flux intensity through a medium. For instance, dark glasses attenuate sunlight, lead attenuates X-rays, and water and air attenuate both light and sound at variable att ...
(normalized to transmission length) as a function of frequency, leading to attenuation distortion
Attenuation distortion is the distortion of an analog signal that occurs during transmission when the transmission medium does not have a flat frequency response across the bandwidth of the medium or the frequency spectrum of the signal.Rowe, St ...
; this is not dispersion, although sometimes reflections at closely spaced impedance boundaries (e.g. crimped segments in a cable) can produce signal distortion with further aggravates inconsistent transit time as observed across signal bandwidth.
Examples
The most familiar example of dispersion is probably arainbow
A rainbow is a meteorological phenomenon that is caused by reflection, refraction and dispersion of light in water droplets resulting in a spectrum of light appearing in the sky. It takes the form of a multicoloured circular arc. Rainbows c ...
, in which dispersion causes the spatial separation of a white light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 tera ...
into components of different wavelengths
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats.
It is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, tr ...
(different color
Color (American English) or colour (British English) is the visual perceptual property deriving from the spectrum of light interacting with the photoreceptor cells of the eyes. Color categories and physical specifications of color are associ ...
s). However, dispersion also has an effect in many other circumstances: for example, group velocity dispersion
In optics, group velocity dispersion (GVD) is a characteristic of a dispersive medium, used most often to determine how the medium will affect the duration of an optical pulse traveling through it. Formally, GVD is defined as the derivative of the ...
causes pulses
In medicine, a pulse represents the tactile arterial palpation of the cardiac cycle (heartbeat) by trained fingertips. The pulse may be palpated in any place that allows an artery to be compressed near the surface of the body, such as at the nec ...
to spread in optical fiber
An optical fiber, or optical fibre in Commonwealth English, is a flexible, transparent fiber made by drawing glass (silica) or plastic to a diameter slightly thicker than that of a human hair. Optical fibers are used most often as a means to ...
s, degrading signals over long distances; also, a cancellation between group-velocity dispersion and nonlinear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...
effects leads to soliton
In mathematics and physics, a soliton or solitary wave is a self-reinforcing wave packet that maintains its shape while it propagates at a constant velocity. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium ...
waves.
Material and waveguide dispersion
Most often, chromatic dispersion refers to bulk material dispersion, that is, the change inrefractive index
In optics, the refractive index (or refraction index) of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
The refractive index determines how much the path of light is bent, or ...
with optical frequency. However, in a waveguide
A waveguide is a structure that guides waves, such as electromagnetic waves or sound, with minimal loss of energy by restricting the transmission of energy to one direction. Without the physical constraint of a waveguide, wave intensities de ...
there is also the phenomenon of ''waveguide dispersion'', in which case a wave's phase velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, ...
in a structure depends on its frequency simply due to the structure's geometry. More generally, "waveguide" dispersion can occur for waves propagating through any inhomogeneous structure (e.g., a photonic crystal
A photonic crystal is an optical nanostructure in which the refractive index changes periodically. This affects the propagation of light in the same way that the structure of Crystal structure, natural crystals gives rise to X-ray crystallograp ...
), whether or not the waves are confined to some region. In a waveguide, ''both'' types of dispersion will generally be present, although they are not strictly additive. For example, in fiber optics the material and waveguide dispersion can effectively cancel each other out to produce a zero-dispersion wavelength
In a single-mode optical fiber, the zero-dispersion wavelength is the wavelength or wavelengths at which material dispersion and waveguide dispersion cancel one another. In all silica-based optical fibers, minimum material dispersion occurs natural ...
, important for fast fiber-optic communication
Fiber-optic communication is a method of transmitting information from one place to another by sending pulses of infrared light through an optical fiber. The light is a form of carrier wave that is modulated to carry information. Fiber is pref ...
.
Material dispersion in optics
spectrometer
A spectrometer () is a scientific instrument used to separate and measure spectral components of a physical phenomenon. Spectrometer is a broad term often used to describe instruments that measure a continuous variable of a phenomenon where the ...
s and spectroradiometer A spectroradiometer is a light measurement tool that is able to measure both the wavelength and amplitude of the light emitted from a light source. Spectrometers discriminate the wavelength based on the position the light hits at the detector array ...
s. However, in lenses, dispersion causes chromatic aberration
In optics, chromatic aberration (CA), also called chromatic distortion and spherochromatism, is a failure of a lens to focus all colors to the same point. It is caused by dispersion: the refractive index of the lens elements varies with the wave ...
, an undesired effect that may degrade images in microscopes, telescopes, and photographic objectives.
The ''phase velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, ...
'', ''v'', of a wave in a given uniform medium is given by
:
where ''c'' is the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant that is important in many areas of physics. The speed of light is exactly equal to ). According to the special theory of relativity, is the upper limit ...
in a vacuum and ''n'' is the refractive index
In optics, the refractive index (or refraction index) of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
The refractive index determines how much the path of light is bent, or ...
of the medium.
In general, the refractive index is some function of the frequency ''f'' of the light, thus ''n'' = ''n''(''f''), or alternatively, with respect to the wave's wavelength ''n'' = ''n''(''λ''). The wavelength dependence of a material's refractive index is usually quantified by its Abbe number
In optics and lens design, the Abbe number, also known as the V-number or constringence of a transparent material, is an approximate measure of the material's dispersion (change of refractive index versus wavelength), with high values of ''V'' in ...
or its coefficients in an empirical formula such as the Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He w ...
or Sellmeier equations.
Because of the Kramers–Kronig relations
The Kramers–Kronig relations are bidirectional mathematical relations, connecting the real and imaginary parts of any complex function that is analytic in the upper half-plane. The relations are often used to compute the real part from the imag ...
, the wavelength dependence of the real part of the refractive index is related to the material absorption
Absorption may refer to:
Chemistry and biology
* Absorption (biology), digestion
**Absorption (small intestine)
*Absorption (chemistry), diffusion of particles of gas or liquid into liquid or solid materials
*Absorption (skin), a route by which ...
, described by the imaginary part of the refractive index (also called the extinction coefficient). In particular, for non-magnetic materials ( ''μ'' = ''μ''0), the susceptibility ''χ'' that appears in the Kramers–Kronig relations is the electric susceptibility
In electricity (electromagnetism), the electric susceptibility (\chi_; Latin: ''susceptibilis'' "receptive") is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applie ...
''χ''e = ''n''2 − 1.
The most commonly seen consequence of dispersion in optics is the separation of white light into a color spectrum
The visible spectrum is the portion of the electromagnetic spectrum that is visual perception, visible to the human eye. Electromagnetic radiation in this range of wavelengths is called ''visible light'' or simply light. A typical human eye wil ...
by a prism
Prism usually refers to:
* Prism (optics), a transparent optical component with flat surfaces that refract light
* Prism (geometry), a kind of polyhedron
Prism may also refer to:
Science and mathematics
* Prism (geology), a type of sedimentary ...
. From Snell's law
Snell's law (also known as Snell–Descartes law and ibn-Sahl law and the law of refraction) is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through ...
it can be seen that the angle of refraction
In physics, refraction is the redirection of a wave as it passes from one medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commonly observed phenomeno ...
of light in a prism depends on the refractive index of the prism material. Since that refractive index varies with wavelength, it follows that the angle that the light is refracted by will also vary with wavelength, causing an angular separation of the colors known as ''angular dispersion''.
For visible light, refraction indices ''n'' of most transparent materials (e.g., air, glasses) decrease with increasing wavelength ''λ'':
:
or alternatively:
:
In this case, the medium is said to have ''normal dispersion''. Whereas, if the index increases with increasing wavelength (which is typically the case in the ultraviolet), the medium is said to have ''anomalous dispersion''.
At the interface of such a material with air or vacuum (index of ~1), Snell's law predicts that light incident at an angle ''θ'' to the normal Normal(s) or The Normal(s) may refer to:
Film and television
* ''Normal'' (2003 film), starring Jessica Lange and Tom Wilkinson
* ''Normal'' (2007 film), starring Carrie-Anne Moss, Kevin Zegers, Callum Keith Rennie, and Andrew Airlie
* ''Norma ...
will be refracted at an angle arcsin(). Thus, blue light, with a higher refractive index, will be bent more strongly than red light, resulting in the well-known rainbow
A rainbow is a meteorological phenomenon that is caused by reflection, refraction and dispersion of light in water droplets resulting in a spectrum of light appearing in the sky. It takes the form of a multicoloured circular arc. Rainbows c ...
pattern.
Group velocity dispersion
 Beyond simply describing a change in the phase velocity over wavelength, a more serious consequence of dispersion in many applications is termed
Beyond simply describing a change in the phase velocity over wavelength, a more serious consequence of dispersion in many applications is termed group velocity dispersion
In optics, group velocity dispersion (GVD) is a characteristic of a dispersive medium, used most often to determine how the medium will affect the duration of an optical pulse traveling through it. Formally, GVD is defined as the derivative of the ...
(GVD). While phase velocity ''v'' is defined as ''v'' = , this describes only one frequency component. When different frequency components are combined, as when considering a signal or a pulse, one is often more interested in the group velocity
The group velocity of a wave is the velocity with which the overall envelope shape of the wave's amplitudes—known as the ''modulation'' or ''envelope'' of the wave—propagates through space.
For example, if a stone is thrown into the middl ...
which describes the speed at which a pulse or information superimposed on a wave (modulation) propagates. In the accompanying animation, it can be seen that the wave itself (orange-brown) travels at a phase velocity which is much faster than the speed of the ''envelope'' (black) which corresponds to the group velocity. This pulse might be a communications signal, for instance, and its information only travels at the group velocity rate even though it consists of wavefronts advancing at a faster rate (the phase velocity).
It is possible to calculate the group velocity from the refractive index curve ''n''(''ω'') or more directly from the wavenumber ''k'' = ''ωn''/''c'' where ''ω'' is the radian frequency ''ω''=2''πf''. Whereas one expression for the phase velocity is ''vp=ω/k'', the group velocity can be expressed using the derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. F ...
: ''v''g=''dω/dk''. Or in terms of the phase velocity ''vp'',
:
When dispersion is present, not only will the group velocity not be equal to the phase velocity, but generally will itself vary with wavelength. This is known as group velocity dispersion and causes a short pulse of light to be broadened, as the different frequency components within the pulse travel at different velocities. Group velocity dispersion is quantified as the derivative of the ''reciprocal'' of the group velocity with respect to radian frequency which results in ''group velocity dispersion'' = .
If a light pulse is propagated through a material with positive group-velocity dispersion, then the shorter wavelength components travel slower than the longer wavelength components. The pulse therefore becomes ''positively chirp
A chirp is a signal in which the frequency increases (''up-chirp'') or decreases (''down-chirp'') with time. In some sources, the term ''chirp'' is used interchangeably with sweep signal. It is commonly applied to sonar, radar, and laser system ...
ed'', or ''up-chirped'', increasing in frequency with time. On the other hand, if a pulse travels through a material with negative group-velocity dispersion, shorter wavelength components travel faster than the longer ones, and the pulse becomes ''negatively chirped'', or ''down-chirped'', decreasing in frequency with time.
An everyday example of a negatively chirped signal in the acoustic domain is that of an approaching train hitting deformities on a welded track. The sound caused by the train itself is impulsive, and travels much faster in the metal tracks than in air, so that the train can be heard well before it arrives. However from afar it isn't heard as causing impulses, but leads to a distinctive descending chirp, amidst reverberation caused by the complexity of the vibrational modes of the track. Group velocity dispersion can be heard in that the volume of the sounds stays audible for a surprisingly long time, up to several seconds.
The ''group velocity dispersion parameter'':
:
is often used to quantify GVD, that is proportional to ''D'' through a negative factor:
:
According to some authors a medium is said to have ''normal dispersion''/''anomalous dispersion'' for a certain vacuum wavelength ''λ''0 if the ''second'' derivative of the refraction index calculated in ''λ''0 is positive/negative or, equivalently, if ''D''(''λ''0) is negative/positive. This definition concerns group velocity dispersion and should not be confused with the one given in previous section. The two definitions do not coincide in general, so the reader has to understand the context.
Dispersion control
The result of GVD, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on optical fiber, since if dispersion is too high, a group of pulses representing a bit-stream will spread in time and merge, rendering the bit-stream unintelligible. This limits the length of fiber that a signal can be sent down without regeneration. One possible answer to this problem is to send signals down the optical fibre at a wavelength where the GVD is zero (e.g., around 1.3–1.5 μm insilica
Silicon dioxide, also known as silica, is an oxide of silicon with the chemical formula , most commonly found in nature as quartz and in various living organisms. In many parts of the world, silica is the major constituent of sand. Silica is one ...
fibres
Fiber or fibre (from la, fibra, links=no) is a natural or artificial substance that is significantly longer than it is wide. Fibers are often used in the manufacture of other materials. The strongest engineering materials often incorporate ...
), so pulses at this wavelength suffer minimal spreading from dispersion. In practice, however, this approach causes more problems than it solves because zero GVD unacceptably amplifies other nonlinear effects (such as four wave mixing Four-wave mixing (FWM) is an intermodulation phenomenon in nonlinear optics, whereby interactions between two or three wavelengths produce two or one new wavelengths. It is similar to the third-order intercept point in electrical systems. Four-wave ...
). Another possible option is to use soliton
In mathematics and physics, a soliton or solitary wave is a self-reinforcing wave packet that maintains its shape while it propagates at a constant velocity. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium ...
pulses in the regime of negative dispersion, a form of optical pulse which uses a nonlinear optical
Nonlinear optics (NLO) is the branch of optics that describes the behaviour of light in ''nonlinear media'', that is, media in which the polarization density P responds non-linearly to the electric field E of the light. The non-linearity is typic ...
effect to self-maintain its shape. Solitons have the practical problem, however, that they require a certain power level to be maintained in the pulse for the nonlinear effect to be of the correct strength. Instead, the solution that is currently used in practice is to perform dispersion compensation, typically by matching the fiber with another fiber of opposite-sign dispersion so that the dispersion effects cancel; such compensation is ultimately limited by nonlinear effects such as self-phase modulation Self-phase modulation (SPM) is a nonlinear optical effect of light–matter interaction.
An ultrashort pulse of light, when travelling in a medium, will induce a varying refractive index of the medium due to the optical Kerr effect. This variation i ...
, which interact with dispersion to make it very difficult to undo.
Dispersion control is also important in laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of electromagnetic radiation. The word "laser" is an acronym for "light amplification by stimulated emission of radiation". The fir ...
s that produce short pulses. The overall dispersion of the optical resonator An optical cavity, resonating cavity or optical resonator is an arrangement of mirrors or other optical elements that forms a cavity resonator for light waves. Optical cavities are a major component of lasers, surrounding the gain medium and provi ...
is a major factor in determining the duration of the pulses emitted by the laser. A pair of prisms can be arranged to produce net negative dispersion, which can be used to balance the usually positive dispersion of the laser medium. Diffraction grating
In optics, a diffraction grating is an optical component with a periodic structure that diffracts light into several beams travelling in different directions (i.e., different diffraction angles). The emerging coloration is a form of structura ...
s can also be used to produce dispersive effects; these are often used in high-power laser amplifier systems. Recently, an alternative to prisms and gratings has been developed: chirped mirror
A chirped mirror is a dielectric mirror with chirped spaces—spaces of varying depth designed to reflect varying wavelengths of lights—between the dielectric layers (stack).
Chirped mirrors are used in applications like lasers to reflect ...
s. These dielectric mirrors are coated so that different wavelengths have different penetration lengths, and therefore different group delays. The coating layers can be tailored to achieve a net negative dispersion.
In waveguides
Waveguide
A waveguide is a structure that guides waves, such as electromagnetic waves or sound, with minimal loss of energy by restricting the transmission of energy to one direction. Without the physical constraint of a waveguide, wave intensities de ...
s are highly dispersive due to their geometry (rather than just to their material composition). Optical fiber
An optical fiber, or optical fibre in Commonwealth English, is a flexible, transparent fiber made by drawing glass (silica) or plastic to a diameter slightly thicker than that of a human hair. Optical fibers are used most often as a means to ...
s are a sort of waveguide for optical frequencies (light) widely used in modern telecommunications systems. The rate at which data can be transported on a single fiber is limited by pulse broadening due to chromatic dispersion among other phenomena.
In general, for a waveguide mode with an angular frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit tim ...
''ω''(''β'') at a propagation constant
The propagation constant of a sinusoidal electromagnetic wave is a measure of the change undergone by the amplitude and phase of the wave as it propagates in a given direction. The quantity being measured can be the voltage, the current in a cir ...
''β'' (so that the electromagnetic fields in the propagation direction ''z'' oscillate proportional to ''e''''i''(''βz''−''ωt'')), the group-velocity dispersion parameter ''D'' is defined as:
:
where ''λ'' = is the vacuum wavelength and ''v''g = is the group velocity. This formula generalizes the one in the previous section for homogeneous media, and includes both waveguide dispersion and material dispersion. The reason for defining the dispersion in this way is that , ''D'', is the (asymptotic) temporal pulse spreading Δ''t'' per unit bandwidth
Δ''λ'' per unit distance travelled, commonly reported in ps/ nm/ km for optical fibers.
In the case of multi-mode optical fiber
Multi-mode optical fiber is a type of optical fiber mostly used for communication over short distances, such as within a building or on a campus. Multi-mode links can be used for data rates up to 100 Gbit/s. Multi-mode fiber has a fairly large ...
s, so-called modal dispersion
Modal dispersion is a distortion mechanism occurring in multimode fibers and other waveguides, in which the signal is spread in time because the propagation velocity of the optical signal is not the same for all modes. Other names for this phenom ...
will also lead to pulse broadening. Even in single-mode fiber
A transverse mode of electromagnetic radiation is a particular electromagnetic field pattern of the radiation in the plane perpendicular (i.e., transverse) to the radiation's propagation direction. Transverse modes occur in radio waves and microwav ...
s, pulse broadening can occur as a result of polarization mode dispersion
Polarization mode dispersion (PMD) is a form of modal dispersion where two different polarizations of light in a waveguide, which normally travel at the same speed, travel at different speeds due to random imperfections and asymmetries, causing ...
(since there are still two polarization modes). These are ''not'' examples of chromatic dispersion as they are not dependent on the wavelength or bandwidth
Bandwidth commonly refers to:
* Bandwidth (signal processing) or ''analog bandwidth'', ''frequency bandwidth'', or ''radio bandwidth'', a measure of the width of a frequency range
* Bandwidth (computing), the rate of data transfer, bit rate or thr ...
of the pulses propagated.
Higher-order dispersion over broad bandwidths
When a broad range of frequencies (a broad bandwidth) is present in a single wavepacket, such as in anultrashort pulse
In optics, an ultrashort pulse, also known as an ultrafast event, is an electromagnetic pulse whose time duration is of the order of a picosecond (10−12 second) or less. Such pulses have a broadband optical spectrum, and can be created by ...
or a chirp
A chirp is a signal in which the frequency increases (''up-chirp'') or decreases (''down-chirp'') with time. In some sources, the term ''chirp'' is used interchangeably with sweep signal. It is commonly applied to sonar, radar, and laser system ...
ed pulse or other forms of spread spectrum
In telecommunication and radio communication, spread-spectrum techniques are methods by which a signal (e.g., an electrical, electromagnetic, or acoustic signal) generated with a particular bandwidth is deliberately spread in the frequency dom ...
transmission, it may not be accurate to approximate the dispersion by a constant over the entire bandwidth, and more complex calculations are required to compute effects such as pulse spreading.
In particular, the dispersion parameter ''D'' defined above is obtained from only one derivative of the group velocity. Higher derivatives are known as ''higher-order dispersion''. These terms are simply a Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor serie ...
expansion of the dispersion relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the d ...
''β''(''ω'') of the medium or waveguide around some particular frequency. Their effects can be computed via numerical evaluation of Fourier transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, ...
s of the waveform, via integration of higher-order slowly varying envelope approximations, by a split-step method In numerical analysis, the split-step (Fourier) method is a pseudo-spectral numerical method used to solve nonlinear partial differential equations like the nonlinear Schrödinger equation. The name arises for two reasons. First, the method relies ...
(which can use the exact dispersion relation rather than a Taylor series), or by direct simulation of the full Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits.
...
rather than an approximate envelope equation.
Generalized formulation of the high orders of dispersion – Lah-Laguerre optics
The description of the chromatic dispersion in a perturbative manner through Taylor coefficients is advantageous for optimization problems where the dispersion from several different systems needs to be balanced. For example, in chirp pulse laser amplifiers, the pulses are first stretched in time by a stretcher to avoid optical damage. Then in the amplification process, the pulses accumulate inevitably linear and nonlinear phase passing through materials. And lastly, the pulses are compressed in various types of compressors. To cancel any residual higher orders in the accumulated phase, usually individual orders are measured and balanced. However, for uniform systems, such perturbative description is often not needed (i.e., propagation in waveguides). The dispersion orders have been generalized in a computationally friendly manner, in the form of Lah-Laguerre type transforms. The dispersion orders are defined by the Taylor expansion of the phase or the wavevector. The dispersion relations for the wavector and the phase can be expressed as: , The derivatives of any differentiable function in the wavelength or the frequency space is specified through a Lah transform as: The matrix elements of the transformation are the Lah coefficients: Written for the GDD the above expression states that a constant with wavelength GGD, will have zero higher orders. The higher orders evaluated from the GDD are: Substituting equation (2) expressed for the refractive index or optical path into equation (1) results in closed-form expressions for the dispersion orders. In general the order dispersion POD is a Laguerre type transform of negative order two: The matrix elements of the transforms are the unsigned Laguerre coefficients of order minus 2, and are given as: The first ten dispersion orders, explicitly written for the wavevector, are: The group refractive index is defined as: . Explicitly, written for the phase , the first ten dispersion orders can be expressed as a function of wavelength using the Lah transforms (equation (2)) as:Spatial dispersion
In electromagnetics and optics, the term ''dispersion'' generally refers to aforementioned temporal or frequency dispersion. Spatial dispersion refers to the non-local response of the medium to the space; this can be reworded as the wavevector dependence of the permittivity. For an exemplaryanisotropic
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physic ...
medium, the spatial relation between electric
Electricity is the set of physical phenomena associated with the presence and motion of matter that has a property of electric charge. Electricity is related to magnetism, both being part of the phenomenon of electromagnetism, as described by ...
and electric displacement field
In physics, the electric displacement field (denoted by D) or electric induction is a vector field that appears in Maxwell's equations. It accounts for the effects of free and bound charge within materials. "D" stands for "displacement", as in ...
can be expressed as a convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions ( and ) that produces a third function (f*g) that expresses how the shape of one is ...
:
:
where the kernel
Kernel may refer to:
Computing
* Kernel (operating system), the central component of most operating systems
* Kernel (image processing), a matrix used for image convolution
* Compute kernel, in GPGPU programming
* Kernel method, in machine learnin ...
is dielectric response (susceptibility); its indices make it in general a tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tenso ...
to account for the anisotropy of the medium. Spatial dispersion is negligible in most macroscopic cases, where the scale of variation of is much larger than atomic dimensions, because the dielectric kernel dies out at macroscopic distances. Nevertheless, it can result in non-negligible macroscopic effects, particularly in conducting media such as metal
A metal (from Greek μέταλλον ''métallon'', "mine, quarry, metal") is a material that, when freshly prepared, polished, or fractured, shows a lustrous appearance, and conducts electricity and heat relatively well. Metals are typicall ...
s, electrolyte
An electrolyte is a medium containing ions that is electrically conducting through the movement of those ions, but not conducting electrons. This includes most soluble salts, acids, and bases dissolved in a polar solvent, such as water. Upon dis ...
s and plasma
Plasma or plasm may refer to:
Science
* Plasma (physics), one of the four fundamental states of matter
* Plasma (mineral), a green translucent silica mineral
* Quark–gluon plasma, a state of matter in quantum chromodynamics
Biology
* Blood pla ...
s. Spatial dispersion also plays role in optical activity
Optical rotation, also known as polarization rotation or circular birefringence, is the rotation of the orientation of the plane of polarization about the optical axis of linearly polarized light as it travels through certain materials. Circul ...
and Doppler broadening
In atomic physics, Doppler broadening is broadening of spectral lines due to the Doppler effect caused by a distribution of velocities of atoms or molecules. Different velocities of the emitting (or absorbing) particles result in different Dopp ...
, as well as in the theory of metamaterial
A metamaterial (from the Greek word μετά ''meta'', meaning "beyond" or "after", and the Latin word ''materia'', meaning "matter" or "material") is any material engineered to have a property that is not found in naturally occurring materials. ...
s.
In gemology
In thetechnical terminology
Jargon is the specialized terminology associated with a particular field or area of activity. Jargon is normally employed in a particular Context (language use), communicative context and may not be well understood outside that context. The conte ...
of gemology
Gemology or gemmology is the science dealing with natural and artificial gemstone materials. It is a geoscience and a branch of mineralogy. Some jewelers (and many non-jewelers) are academically trained gemologists and are qualified to identify a ...
, ''dispersion'' is the difference in the refractive index of a material at the B and G (686.7 nm and 430.8 nm) or C and F (656.3 nm and 486.1 nm) Fraunhofer wavelengths, and is meant to express the degree to which a prism cut from the gemstone
A gemstone (also called a fine gem, jewel, precious stone, or semiprecious stone) is a piece of mineral crystal which, in cut and polished form, is used to make jewelry or other adornments. However, certain rocks (such as lapis lazuli, opal, ...
demonstrates "fire". Fire is a colloquial term used by gemologists to describe a gemstone's dispersive nature or lack thereof. Dispersion is a material property. The amount of fire demonstrated by a given gemstone is a function of the gemstone's facet angles, the polish quality, the lighting environment, the material's refractive index, the saturation of color, and the orientation of the viewer relative to the gemstone.
In imaging
In photographic and microscopic lenses, dispersion causeschromatic aberration
In optics, chromatic aberration (CA), also called chromatic distortion and spherochromatism, is a failure of a lens to focus all colors to the same point. It is caused by dispersion: the refractive index of the lens elements varies with the wave ...
, which causes the different colors in the image not to overlap properly. Various techniques have been developed to counteract this, such as the use of achromat
An achromatic lens or achromat is a lens that is designed to limit the effects of chromatic and spherical aberration. Achromatic lenses are corrected to bring two wavelengths (typically red and blue) into focus on the same plane.
The most comm ...
s, multielement lenses with glasses of different dispersion. They are constructed in such a way that the chromatic aberrations of the different parts cancel out.
Pulsar emissions
Pulsar
A pulsar (from ''pulsating radio source'') is a highly magnetized rotating neutron star that emits beams of electromagnetic radiation out of its magnetic poles. This radiation can be observed only when a beam of emission is pointing toward Ea ...
s are spinning neutron stars that emit pulse
In medicine, a pulse represents the tactile arterial palpation of the cardiac cycle (heartbeat) by trained fingertips. The pulse may be palpated in any place that allows an artery to be compressed near the surface of the body, such as at the nec ...
s at very regular intervals ranging from milliseconds to seconds. Astronomers believe that the pulses are emitted simultaneously over a wide range of frequencies. However, as observed on Earth, the components of each pulse emitted at higher radio frequencies arrive before those emitted at lower frequencies. This dispersion occurs because of the ionized component of the interstellar medium
In astronomy, the interstellar medium is the matter and radiation that exist in the space between the star systems in a galaxy. This matter includes gas in ionic, atomic, and molecular form, as well as dust and cosmic rays. It fills interstella ...
, mainly the free electrons, which make the group velocity frequency dependent. The extra delay added at a frequency is
:
where the dispersion constant ''k''DM is given by
:
and the dispersion measure (DM) is the column density of free electrons (total electron content
Total electron content (TEC) is an important descriptive quantity for the ionosphere of the Earth. TEC is the total number of electrons integrated between two points, along a tube of one meter squared cross section, i.e., the electron columnar n ...
) — i.e. the number density of electrons ''n''e (electrons/cm3) integrated along the path traveled by the photon from the pulsar to the Earth — and is given by
:
with units of parsec
The parsec (symbol: pc) is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to or (au), i.e. . The parsec unit is obtained by the use of parallax and trigonometry, and ...
s per cubic centimetre (1 pc/cm3 = 30.857 × 1021 m−2).Lorimer, D.R., and Kramer, M., ''Handbook of Pulsar Astronomy'', vol. 4 of Cambridge Observing Handbooks for Research Astronomers, (Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press
A university press is an academic publishing hou ...
, Cambridge, U.K.; New York, U.S.A, 2005), 1st edition.
Typically for astronomical observations, this delay cannot be measured directly, since the emission time is unknown. What ''can'' be measured is the difference in arrival times at two different frequencies. The delay Δ''t'' between a high frequency hi and a low frequency lo component of a pulse will be
:
Rewriting the above equation in terms of Δ''t'' allows one to determine the DM by measuring pulse arrival times at multiple frequencies. This in turn can be used to study the interstellar medium, as well as allow for observations of pulsars at different frequencies to be combined.
See also
*Abbe number
In optics and lens design, the Abbe number, also known as the V-number or constringence of a transparent material, is an approximate measure of the material's dispersion (change of refractive index versus wavelength), with high values of ''V'' in ...
* Calculation of glass properties
The calculation of glass properties (glass modeling) is used to predict glass properties of interest or glass behavior under certain conditions (e.g., during production) without experimental investigation, based on past data and experience, with t ...
incl. dispersion
* Cauchy's equation
In optics, Cauchy's transmission equation is an empirical relationship between the refractive index and wavelength of light for a particular transparent material. It is named for the mathematician Augustin-Louis Cauchy, who defined it in 1837 ...
* Dispersion relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the d ...
* Fast radio burst
In radio astronomy, a fast radio burst (FRB) is a transient radio pulse of length ranging from a fraction of a millisecond to 3 seconds, caused by some high-energy astrophysical process not yet understood. Astronomers estimate the average FRB rel ...
(astronomy)
* Fluctuation theorem
The fluctuation theorem (FT), which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium (i.e., maximum entropy) will increase or decrease ov ...
* Green–Kubo relations
The Green–Kubo relations ( Melville S. Green 1954, Ryogo Kubo 1957) give the exact mathematical expression for transport coefficients \gamma in terms of integrals of time correlation functions:
:\gamma = \int_0^\infty \left\langle \dot(t) \dot ...
* Group delay
In signal processing, group delay and phase delay are delay times experienced by a signal's various frequency components when the signal passes through a system that is linear time-invariant (LTI), such as a microphone, coaxial cable, amplifier, l ...
* Intramodal dispersion
* Kramers–Kronig relations
The Kramers–Kronig relations are bidirectional mathematical relations, connecting the real and imaginary parts of any complex function that is analytic in the upper half-plane. The relations are often used to compute the real part from the imag ...
* Linear response function A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response. Because of its many applications in information t ...
* Multiple-prism dispersion theory
The first description of multiple-prism arrays, and multiple-prism dispersion, was given by Newton in his book ''Opticks''. Prism pair expanders were introduced by Brewster in 1813. A modern mathematical description of the single-prism dispersio ...
* Sellmeier equation
* Ultrashort pulse
In optics, an ultrashort pulse, also known as an ultrafast event, is an electromagnetic pulse whose time duration is of the order of a picosecond (10−12 second) or less. Such pulses have a broadband optical spectrum, and can be created by ...
* Virtually imaged phased array
A virtually imaged phased array (VIPA) is an angular Dispersion (optics), dispersive device that, like a Prism (optics), prism or a diffraction grating, splits light into its Electromagnetic spectrum, spectral components. It works almost independ ...
References
External links
Dispersive Wiki
– discussing the mathematical aspects of dispersion.
– Encyclopedia of Laser Physics and Technology
Animations demonstrating optical dispersion
by QED
Interactive webdemo for chromatic dispersion
Institute of Telecommunications, University of Stuttgart {{Authority control Glass physics Optics