|
Gas
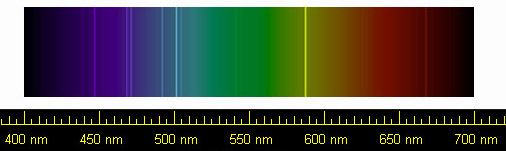
Gas is one of the four fundamental states of matter (the others being solid, liquid, and plasma). A pure gas may be made up of individual atoms (e.g. a noble gas like neon), elemental molecules made from one type of atom (e.g. oxygen), or compound molecules made from a variety of atoms (e.g. carbon dioxide). A gas mixture, such as air, contains a variety of pure gases. What distinguishes a gas from liquids and solids is the vast separation of the individual gas particles. This separation usually makes a colourless gas invisible to the human observer. The gaseous state of matter occurs between the liquid and plasma states, the latter of which provides the upper temperature boundary for gases. Bounding the lower end of the temperature scale lie degenerative quantum gases which are gaining increasing attention. High-density atomic gases super-cooled to very low temperatures are classified by their statistical behavior as either Bose gases or Fermi gases. For a comprehensive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noble Gas
The noble gases (historically also the inert gases; sometimes referred to as aerogens) make up a class of chemical elements with similar properties; under standard conditions, they are all odorless, colorless, monatomic gases with very low chemical reactivity. The six naturally occurring noble gases are helium (He), neon (Ne), argon (Ar), krypton (Kr), xenon (Xe), and the radioactive radon (Rn). Oganesson (Og) is a synthetically produced highly radioactive element. Although IUPAC has used the term "noble gas" interchangeably with "group 18" and thus included oganesson, it may not be significantly chemically noble and is predicted to break the trend and be reactive due to relativistic effects. Because of the extremely short 0.7 ms half-life of its only known isotope, its chemistry has not yet been investigated. For the first six periods of the periodic table, the noble gases are exactly the members of group 18. Noble gases are typically highly unreactive except whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noble Gases
The noble gases (historically also the inert gases; sometimes referred to as aerogens) make up a class of chemical elements with similar properties; under standard conditions, they are all odorless, colorless, monatomic gases with very low chemical reactivity. The six naturally occurring noble gases are helium (He), neon (Ne), argon (Ar), krypton (Kr), xenon (Xe), and the radioactive radon (Rn). Oganesson (Og) is a synthetically produced highly radioactive element. Although IUPAC has used the term "noble gas" interchangeably with "group 18" and thus included oganesson, it may not be significantly chemically noble and is predicted to break the trend and be reactive due to relativistic effects. Because of the extremely short 0.7 ms half-life of its only known isotope, its chemistry has not yet been investigated. For the first six periods of the periodic table, the noble gases are exactly the members of group 18. Noble gases are typically highly unreactive except whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helium
Helium (from el, ἥλιος, helios, lit=sun) is a chemical element with the symbol He and atomic number 2. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas and the first in the noble gas group in the periodic table. Its boiling and melting point are the lowest among all the elements. It is the second lightest and second most abundant element in the observable universe ( hydrogen is the lightest and most abundant). It is present at about 24% of the total elemental mass, which is more than 12 times the mass of all the heavier elements combined. Its abundance is similar to this in both the Sun and in Jupiter, due to the very high nuclear binding energy (per nucleon) of helium-4, with respect to the next three elements after helium. This helium-4 binding energy also accounts for why it is a product of both nuclear fusion and radioactive decay. The most common isotope of helium in the universe is helium-4, the vast majority of which was forme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chlorine
Chlorine is a chemical element with the symbol Cl and atomic number 17. The second-lightest of the halogens, it appears between fluorine and bromine in the periodic table and its properties are mostly intermediate between them. Chlorine is a yellow-green gas at room temperature. It is an extremely reactive element and a strong oxidising agent: among the elements, it has the highest electron affinity and the third-highest electronegativity on the revised Pauling scale, behind only oxygen and fluorine. Chlorine played an important role in the experiments conducted by medieval alchemists, which commonly involved the heating of chloride salts like ammonium chloride ( sal ammoniac) and sodium chloride (common salt), producing various chemical substances containing chlorine such as hydrogen chloride, mercury(II) chloride (corrosive sublimate), and hydrochloric acid (in the form of ). However, the nature of free chlorine gas as a separate substance was only recognised aroun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxygen
Oxygen is the chemical element with the symbol O and atomic number 8. It is a member of the chalcogen group in the periodic table, a highly reactive nonmetal, and an oxidizing agent that readily forms oxides with most elements as well as with other compounds. Oxygen is Earth's most abundant element, and after hydrogen and helium, it is the third-most abundant element in the universe. At standard temperature and pressure, two atoms of the element bind to form dioxygen, a colorless and odorless diatomic gas with the formula . Diatomic oxygen gas currently constitutes 20.95% of the Earth's atmosphere, though this has changed considerably over long periods of time. Oxygen makes up almost half of the Earth's crust in the form of oxides.Atkins, P.; Jones, L.; Laverman, L. (2016).''Chemical Principles'', 7th edition. Freeman. Many major classes of organic molecules in living organisms contain oxygen atoms, such as proteins, nucleic acids, carbohydrates, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carbon Dioxide
Carbon dioxide ( chemical formula ) is a chemical compound made up of molecules that each have one carbon atom covalently double bonded to two oxygen atoms. It is found in the gas state at room temperature. In the air, carbon dioxide is transparent to visible light but absorbs infrared radiation, acting as a greenhouse gas. It is a trace gas in Earth's atmosphere at 421 parts per million (ppm), or about 0.04% by volume (as of May 2022), having risen from pre-industrial levels of 280 ppm. Burning fossil fuels is the primary cause of these increased CO2 concentrations and also the primary cause of climate change.IPCC (2022Summary for policy makersiClimate Change 2022: Mitigation of Climate Change. Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA Carbon dioxide is soluble in water and is found in groundwater, lakes, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrogen
Hydrogen is the chemical element with the symbol H and atomic number 1. Hydrogen is the lightest element. At standard conditions hydrogen is a gas of diatomic molecules having the formula . It is colorless, odorless, tasteless, non-toxic, and highly combustible. Hydrogen is the most abundant chemical substance in the universe, constituting roughly 75% of all normal matter.However, most of the universe's mass is not in the form of baryons or chemical elements. See dark matter and dark energy. Stars such as the Sun are mainly composed of hydrogen in the plasma state. Most of the hydrogen on Earth exists in molecular forms such as water and organic compounds. For the most common isotope of hydrogen (symbol 1H) each atom has one proton, one electron, and no neutrons. In the early universe, the formation of protons, the nuclei of hydrogen, occurred during the first second after the Big Bang. The emergence of neutral hydrogen atoms throughout the universe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nitrogen
Nitrogen is the chemical element with the symbol N and atomic number 7. Nitrogen is a nonmetal and the lightest member of group 15 of the periodic table, often called the pnictogens. It is a common element in the universe, estimated at seventh in total abundance in the Milky Way and the Solar System. At standard temperature and pressure, two atoms of the element bond to form N2, a colorless and odorless diatomic gas. N2 forms about 78% of Earth's atmosphere, making it the most abundant uncombined element. Nitrogen occurs in all organisms, primarily in amino acids (and thus proteins), in the nucleic acids ( DNA and RNA) and in the energy transfer molecule adenosine triphosphate. The human body contains about 3% nitrogen by mass, the fourth most abundant element in the body after oxygen, carbon, and hydrogen. The nitrogen cycle describes the movement of the element from the air, into the biosphere and organic compounds, then back into the atmosphere. Many indus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Gas
An ideal Fermi gas is a state of matter which is an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi. This physical model can be accurately applied to many systems with many fermions. Some key examples are the behaviour of charge carriers in a metal, nucleons in an atomic nucleus, neutrons in a neutron star, and electrons in a white dwarf. Description An ideal Fermi gas or free Fermi gas is a physical model assuming a collection of non-interacting fermions in a constant potential well. Fermions are elementary or composite particles with half-integer spin, thus follo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bose Gas
An ideal Bose gas is a quantum-mechanical phase of matter, analogous to a classical ideal gas. It is composed of bosons, which have an integer value of spin, and abide by Bose–Einstein statistics. The statistical mechanics of bosons were developed by Satyendra Nath Bose for a photon gas, and extended to massive particles by Albert Einstein who realized that an ideal gas of bosons would form a condensate at a low enough temperature, unlike a classical ideal gas. This condensate is known as a Bose–Einstein condensate. Introduction and examples Bosons are quantum mechanical particles that follow Bose–Einstein statistics, or equivalently, that possess integer spin. These particles can be classified as elementary: these are the Higgs boson, the photon, the gluon, the W/Z and the hypothetical graviton; or composite like the atom of hydrogen, the atom of 16 O, the nucleus of deuterium, mesons etc. Additionally, some quasiparticles in more complex systems can also be c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluorine
Fluorine is a chemical element with the symbol F and atomic number 9. It is the lightest halogen and exists at standard conditions as a highly toxic, pale yellow diatomic gas. As the most electronegative reactive element, it is extremely reactive, as it reacts with all other elements except for the light inert gases. Among the elements, fluorine ranks 24th in universal abundance and 13th in terrestrial abundance. Fluorite, the primary mineral source of fluorine which gave the element its name, was first described in 1529; as it was added to metal ores to lower their melting points for smelting, the Latin verb meaning 'flow' gave the mineral its name. Proposed as an element in 1810, fluorine proved difficult and dangerous to separate from its compounds, and several early experimenters died or sustained injuries from their attempts. Only in 1886 did French chemist Henri Moissan isolate elemental fluorine using low-temperature electrolysis, a process still employed for modern ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
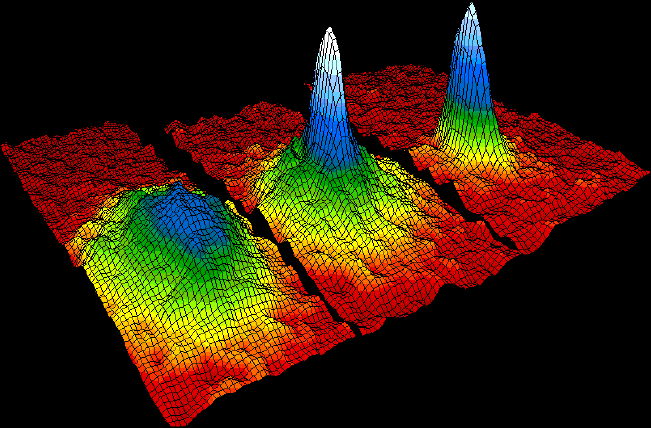
Bose–Einstein Condensate
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low densities is cooled to temperatures very close to absolute zero (−273.15 °C or −459.67 °F). Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which point microscopic quantum mechanical phenomena, particularly wavefunction interference, become apparent macroscopically. A BEC is formed by cooling a gas of extremely low density (about 100,000 times less dense than normal air) to ultra-low temperatures. This state was first predicted, generally, in 1924–1925 by Albert Einstein following and crediting a pioneering paper by Satyendra Nath Bose on the new field now known as quantum statistics. In 1995, the Bose-Einstein condensate was created by Eric Cornell and Carl Wieman of the University of Colorado at Boulder using rubidium atoms; later that year, Wolfgang Ketterle of MIT ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |