Bose–Einstein Condensate

In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low densities is cooled to temperatures very close to absolute zero (−273.15 °C or −459.67 °F). Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which point microscopic quantum mechanical phenomena, particularly wavefunction interference, become apparent macroscopically. A BEC is formed by cooling a gas of extremely low density (about 100,000 times less dense than normal air) to ultra-low temperatures.

This state was first predicted, generally, in 1924–1925 by Albert Einstein following and crediting a pioneering paper by Satyendra Nath Bose on the new field now known as quantum statistics. In 1995, the Bose-Einstein condensate was created by Eric Cornell and Carl Wieman of the University of Colorado at Boulder using rubidium atoms; later that year, Wolfgang Ketterle of MIT produced a BEC using sodium atoms. In 2001 Cornell, Wieman and Ketterle shared the Nobel Prize in Physics "for the achievement of Bose-Einstein condensation in dilute gases of alkali atoms, and for early fundamental studies of the properties of the condensates."

History

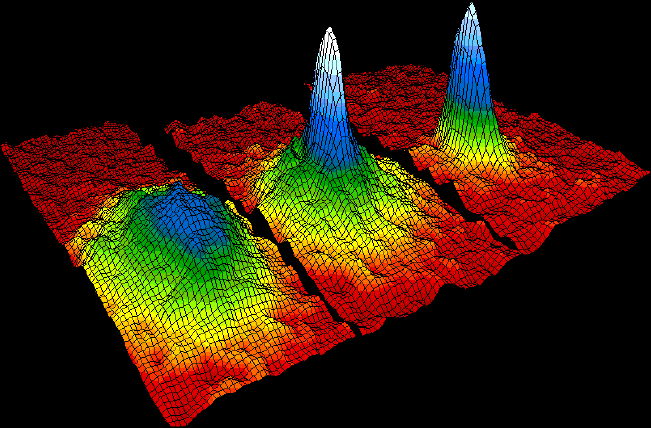
Bose first sent a paper to Einstein on the quantum statistics of light quanta (now called photons), in which he derived Planck's quantum radiation law without any reference to classical physics. Einstein was impressed, translated the paper himself from English to German and submitted it for Bose to the ''Zeitschrift für Physik'', which published it in 1924. (The Einstein manuscript, once believed to be lost, was found in a library at Leiden University in 2005.) Einstein then extended Bose's ideas to matter in two other papers. The result of their efforts is the concept of a Bose gas, governed by Bose–Einstein statistics, which describes the statistical distribution of identical particles with integer spin, now called bosons. Bosons, particles that include the photon as well as atoms such as helium-4 (), are allowed to share a quantum state. Einstein proposed that cooling bosonic atoms to a very low temperature would cause them to fall (or "condense") into the lowest accessible quantum state, resulting in a new form of matter.

In 1938, Fritz London proposed the BEC as a mechanism for superfluidity in and superconductivity.

The quest to produce a Bose–Einstein condensate in the laboratory was stimulated by a paper published in 1976 by two Program Directors at the National Science Foundation (William Stwalley and Lewis Nosanow). This led to the immediate pursuit of the idea by four independent research groups; these were led by Isaac Silvera (University of Amsterdam), Walter Hardy (University of British Columbia), Thomas Greytak (Massachusetts Institute of Technology) and David Lee (Cornell University).

On 5 June 1995, the first gaseous condensate was produced by Eric Cornell and Carl Wieman at the University of Colorado at Boulder NIST–JILA lab, in a gas of rubidium atoms cooled to 170 nanokelvins (nK). Shortly thereafter, Wolfgang Ketterle at MIT produced a Bose–Einstein Condensate in a gas of sodium atoms. For their achievements Cornell, Wieman, and Ketterle received the 2001 Nobel Prize in Physics. These early studies founded the field of ultracold atoms, and hundreds of research groups around the world now routinely produce BECs of dilute atomic vapors in their labs.

Since 1995, many other atomic species have been condensed, and BECs have also been realized using molecules, quasi-particles, and photons.

Critical temperature

This transition to BEC occurs below a critical temperature, which for a uniform three-dimensional gas consisting of non-interacting particles with no apparent internal degrees of freedom is given by:

:$T_=\left(\frac\right)^\frac \approx 3.3125 \ \frac$

where:

:
Interactions shift the value and the corrections can be calculated by mean-field theory.
This formula is derived from finding the gas degeneracy in the Bose gas using Bose–Einstein statistics.

Derivation

Ideal Bose gas

For an ideal Bose gas we have the equation of state:

:$\frac=\fracg_(f)+\frac\frac$

where $v=V/N$ is the per particle volume, $\lambda$ the thermal wavelength, $f$ the fugacity and
:$g_\alpha (f)=\sum \limits_^\infty \frac$

It is noticeable that $g_$ is a monotonically growing function of $f$ in f \in , 1/math>, which are the only values for which the series converge.
Recognizing that the second term on the right-hand side contains the expression for the average occupation number of the fundamental state $\langle n_0 \rangle$, the equation of state can be rewritten as

:$\frac=\fracg_(f)+\frac \Leftrightarrow \frac\lambda^3=\frac-g_(f)$

Because the left term on the second equation must always be positive, $\frac>g_(f)$ and because $g_(f)\le g_(1)$, a stronger condition is

:$\frac>g_(1)$

which defines a transition between a gas phase and a condensed phase. On the critical region it is possible to define a critical temperature and thermal wavelength:

:$\lambda_c^3=g_(1)v=\zeta(3/2)v$

:$T_c=\frac$

recovering the value indicated on the previous section. The critical values are such that if T or $\lambda >\lambda_c$ we are in the presence of a Bose–Einstein condensate.
Understanding what happens with the fraction of particles on the fundamental level is crucial. As so, write the equation of state for $f=1$, obtaining

:$\frac=1-\left(\frac\right)^3$ and equivalently $\frac=1-\left(\frac\right)^$.

So, if $T\ll T_c$ the fraction $\frac \approx 1$ and if $T \gg T_c$ the fraction $\frac \approx 0$. At temperatures near to absolute 0, particles tend to condensate in the fundamental state, which is the state with momentum $\vec=0$.

Models

Bose Einstein's non-interacting gas

Consider a collection of ''N'' non-interacting particles, which can each be in one of two quantum states, $, 0\rangle$ and $, 1\rangle$. If the two states are equal in energy, each different configuration is equally likely.

If we can tell which particle is which, there are $2^N$ different configurations, since each particle can be in $, 0\rangle$ or $, 1\rangle$ independently. In almost all of the configurations, about half the particles are in $, 0\rangle$ and the other half in $, 1\rangle$. The balance is a statistical effect: the number of configurations is largest when the particles are divided equally.

If the particles are indistinguishable, however, there are only ''N''+1 different configurations. If there are ''K'' particles in state $, 1\rangle$, there are particles in state $, 0\rangle$. Whether any particular particle is in state $, 0\rangle$ or in state $, 1\rangle$ cannot be determined, so each value of ''K'' determines a unique quantum state for the whole system.

Suppose now that the energy of state $, 1\rangle$ is slightly greater than the energy of state $, 0\rangle$ by an amount ''E''. At temperature ''T'', a particle will have a lesser probability to be in state $, 1\rangle$ by $e^$. In the distinguishable case, the particle distribution will be biased slightly towards state $, 0\rangle$. But in the indistinguishable case, since there is no statistical pressure toward equal numbers, the most-likely outcome is that most of the particles will collapse into state $, 0\rangle$.

In the distinguishable case, for large ''N'', the fraction in state $, 0\rangle$ can be computed. It is the same as flipping a coin with probability proportional to ''p'' = exp(−''E''/''T'') to land tails.

In the indistinguishable case, each value of ''K'' is a single state, which has its own separate Boltzmann probability. So the probability distribution is exponential:

:$\, P(K)= C e^ = C p^K.$

For large ''N'', the normalization constant ''C'' is . The expected total number of particles not in the lowest energy state, in the limit that $N\rightarrow \infty$, is equal to
: $\sum_ C p^n=p/(1-p)$
It does not grow when ''N'' is large; it just approaches a constant. This will be a negligible fraction of the total number of particles. So a collection of enough Bose particles in thermal equilibrium will mostly be in the ground state, with only a few in any excited state, no matter how small the energy difference.

Consider now a gas of particles, which can be in different momentum states labeled $, k\rangle$. If the number of particles is less than the number of thermally accessible states, for high temperatures and low densities, the particles will all be in different states. In this limit, the gas is classical. As the density increases or the temperature decreases, the number of accessible states per particle becomes smaller, and at some point, more particles will be forced into a single state than the maximum allowed for that state by statistical weighting. From this point on, any extra particle added will go into the ground state.

To calculate the transition temperature at any density, integrate, over all momentum states, the expression for maximum number of excited particles, :

:$\, N = V \int = V \int$
:$\, p(k)= e^.$

When the integral (also known as Bose–Einstein integral) is evaluated with factors of $k_B$ and ℏ restored by dimensional analysis, it gives the critical temperature formula of the preceding section. Therefore, this integral defines the critical temperature and particle number corresponding to the conditions of negligible chemical potential $\mu$. In Bose–Einstein statistics distribution, $\mu$ is actually still nonzero for BECs; however, $\mu$ is less than the ground state energy. Except when specifically talking about the ground state, $\mu$ can be approximated for most energy or momentum states as $\mu \approx 0$.

Bogoliubov theory for weakly interacting gas

Nikolay Bogoliubov considered perturbations on the limit of dilute gas, finding a finite pressure at zero temperature and positive chemical potential. This leads to corrections for the ground state. The Bogoliubov state has pressure (''T'' = 0): $P = gn^2/2$.

The original interacting system can be converted to a system of non-interacting particles with a dispersion law.

Gross–Pitaevskii equation

In some simplest cases, the state of condensed particles can be described with a nonlinear Schrödinger equation, also known as Gross–Pitaevskii or Ginzburg–Landau equation. The validity of this approach is actually limited to the case of ultracold temperatures, which fits well for the most alkali atoms experiments.

This approach originates from the assumption that the state of the BEC can be described by the unique wavefunction of the condensate $\psi(\vec)$. For a system of this nature, $, \psi(\vec), ^2$ is interpreted as the particle density, so the total number of atoms is $N=\int d\vec, \psi(\vec), ^2$

Provided essentially all atoms are in the condensate (that is, have condensed to the ground state), and treating the bosons using mean-field theory, the energy (E) associated with the state $\psi(\vec)$ is:

:E=\int
d\vec\left \nabla\psi(\vec), ^2+V(\vec), \psi(\vec), ^2+\fracU_0, \psi(\vec), ^4\right/math>

Minimizing this energy with respect to infinitesimal variations in $\psi(\vec)$, and holding the number of atoms constant, yields the Gross–Pitaevski equation (GPE) (also a non-linear Schrödinger equation):

:$i\hbar\frac = \left(-\frac+V(\vec)+U_0, \psi(\vec), ^2\right)\psi(\vec)$

where:

:

In the case of zero external potential, the dispersion law of interacting Bose–Einstein-condensed particles is given by so-called Bogoliubov spectrum (for $\ T= 0$):

:$= \sqrt$

The Gross-Pitaevskii equation (GPE) provides a relatively good description of the behavior of atomic BEC's. However, GPE does not take into account the temperature dependence of dynamical variables, and is therefore valid only for $\ T= 0$.
It is not applicable, for example, for the condensates of excitons, magnons and photons, where the critical temperature is comparable to room temperature.

Numerical solution

The Gross-Pitaevskii equation is a partial differential equation in space and time variables. Usually it does not have analytic solution and
different numerical methods, such as split-step
Crank-Nicolson
and Fourier spectral methods, are used for its solution. There are different Fortran and C programs for its solution for contact interaction
and long-range dipolar interaction which can be freely used.

Weaknesses of Gross–Pitaevskii model

The Gross–Pitaevskii model of BEC is a physical approximation valid for certain classes of BECs. By construction, the GPE uses the following simplifications: it assumes that interactions between condensate particles are of the contact two-body type and also neglects anomalous contributions to self-energy. These assumptions are suitable mostly for the dilute three-dimensional condensates. If one relaxes any of these assumptions, the equation for the condensate wavefunction acquires the terms containing higher-order powers of the wavefunction. Moreover, for some physical systems the amount of such terms turns out to be infinite, therefore, the equation becomes essentially non-polynomial. The examples where this could happen are the Bose–Fermi composite condensates, effectively lower-dimensional condensates, and dense condensates and superfluid clusters and droplets. It is found that one has to go beyond the Gross-Pitaevskii equation. For example, the logarithmic term $\psi \ln , \psi, ^2$ found in the Logarithmic Schrödinger equation must be added to the Gross-Pitaevskii equation along with a Ginzburg-Sobyanin contribution to correctly determine that the speed of sound scales as the cubic root of pressure for Helium-4 at very low temperatures in close agreement with experiment.

Other

However, it is clear that in a general case the behaviour of Bose–Einstein condensate can be described by coupled evolution equations for condensate density, superfluid velocity and distribution function of elementary excitations. This problem was solved in 1977 by Peletminskii et al. in microscopical approach. The Peletminskii equations are valid for any finite temperatures below the critical point. Years after, in 1985, Kirkpatrick and Dorfman obtained similar equations using another microscopical approach. The Peletminskii equations also reproduce Khalatnikov hydrodynamical equations for superfluid as a limiting case.

Superfluidity of BEC and Landau criterion

The phenomena of superfluidity of a Bose gas and superconductivity of a strongly-correlated Fermi gas (a gas of Cooper pairs) are tightly connected to Bose–Einstein condensation. Under corresponding conditions, below the temperature of phase transition, these phenomena were observed in helium-4 and different classes of superconductors. In this sense, the superconductivity is often called the superfluidity of Fermi gas. In the simplest form, the origin of superfluidity can be seen from the weakly interacting bosons model.

Experimental observation

Superfluid helium-4

In 1938, Pyotr Kapitsa, John Allen and Don Misener discovered that helium-4 became a new kind of fluid, now known as a superfluid, at temperatures less than 2.17 K (the lambda point). Superfluid helium has many unusual properties, including zero viscosity (the ability to flow without dissipating energy) and the existence of quantized vortices. It was quickly believed that the superfluidity was due to partial Bose–Einstein condensation of the liquid. In fact, many properties of superfluid helium also appear in gaseous condensates created by Cornell, Wieman and Ketterle (see below). Superfluid helium-4 is a liquid rather than a gas, which means that the interactions between the atoms are relatively strong; the original theory of Bose–Einstein condensation must be heavily modified in order to describe it. Bose–Einstein condensation remains, however, fundamental to the superfluid properties of helium-4. Note that helium-3, a fermion, also enters a superfluid phase (at a much lower temperature) which can be explained by the formation of bosonic Cooper pairs of two atoms (see also fermionic condensate).

Dilute atomic gases

The first "pure" Bose–Einstein condensate was created by Eric Cornell, Carl Wieman, and co-workers at JILA on 5 June 1995. They cooled a dilute vapor of approximately two thousand rubidium-87 atoms to below 170 nK using a combination of laser cooling (a technique that won its inventors Steven Chu, Claude Cohen-Tannoudji, and William D. Phillips the 1997 Nobel Prize in Physics) and magnetic evaporative cooling. About four months later, an independent effort led by Wolfgang Ketterle at MIT condensed sodium-23. Ketterle's condensate had a hundred times more atoms, allowing important results such as the observation of quantum mechanical interference between two different condensates. Cornell, Wieman and Ketterle won the 2001 Nobel Prize in Physics for their achievements.

A group led by Randall Hulet at Rice University announced a condensate of lithium atoms only one month following the JILA work. Lithium has attractive interactions, causing the condensate to be unstable and collapse for all but a few atoms. Hulet's team subsequently showed the condensate could be stabilized by confinement quantum pressure for up to about 1000 atoms. Various isotopes have since been condensed.

Velocity-distribution data graph

In the image accompanying this article, the velocity-distribution data indicates the formation of a Bose–Einstein condensate out of a gas of rubidium atoms. The false colors indicate the number of atoms at each velocity, with red being the fewest and white being the most. The areas appearing white and light blue are at the lowest velocities. The peak is not infinitely narrow because of the Heisenberg uncertainty principle: spatially confined atoms have a minimum width velocity distribution. This width is given by the curvature of the magnetic potential in the given direction. More tightly confined directions have bigger widths in the ballistic velocity distribution. This anisotropy of the peak on the right is a purely quantum-mechanical effect and does not exist in the thermal distribution on the left. This graph served as the cover design for the 1999 textbook ''Thermal Physics'' by Ralph Baierlein.

Quasiparticles

Bose–Einstein condensation also applies to quasiparticles in solids. Magnons, excitons, and polaritons have integer spin which means they are bosons that can form condensates.

Magnons, electron spin waves, can be controlled by a magnetic field. Densities from the limit of a dilute gas to a strongly interacting Bose liquid are possible. Magnetic ordering is the analog of superfluidity. In 1999 condensation was demonstrated in antiferromagnetic , at temperatures as great as 14 K. The high transition temperature (relative to atomic gases) is due to the magnons' small mass (near that of an electron) and greater achievable density. In 2006, condensation in a ferromagnetic yttrium-iron-garnet thin film was seen even at room temperature, with optical pumping.

Excitons, electron-hole pairs, were predicted to condense at low temperature and high density by Boer et al., in 1961. Bilayer system experiments first demonstrated condensation in 2003, by Hall voltage disappearance. Fast optical exciton creation was used to form condensates in sub-kelvin in 2005 on.

Polariton condensation was first detected for exciton-polaritons in a quantum well microcavity kept at 5 K.

In zero gravity

In June 2020, the Cold Atom Laboratory experiment on board the International Space Station successfully created a BEC of rubidium atoms and observed them for over a second in free-fall. Although initially just a proof of function, early results showed that, in the microgravity environment of the ISS, about half of the atoms formed into a magnetically insensitive halo-like cloud around the main body of the BEC.

Peculiar properties

Quantized vortices

As in many other systems, vortices can exist in BECs.
Vortices can be created, for example, by "stirring" the condensate with lasers,
rotating the confining trap,
or by rapid cooling across the phase transition.
The vortex created will be a quantum vortex with core shape determined by the interactions. Fluid circulation around any point is quantized due to the single-valued nature of the order BEC order parameter or wavefunction, that can be written in the form $\psi(\vec)=\phi(\rho,z)e^$ where $\rho, z$ and $\theta$ are as in the cylindrical coordinate system, and $\ell$ is the angular quantum number (a.k.a. the "charge" of the vortex). Since the energy of a vortex is proportional to the square of its angular momentum, in trivial topology only $\ell=1$ vortices can exist in the steady state; Higher-charge vortices will have a tendency to split into $\ell=1$ vortices, if allowed by the topology of the geometry.

An axially symmetric (for instance, harmonic) confining potential is commonly used for the study of vortices in BEC. To determine $\phi(\rho,z)$, the energy of $\psi(\vec)$ must be minimized, according to the constraint $\psi(\vec)=\phi(\rho,z)e^$. This is usually done computationally, however, in a uniform medium, the following analytic form demonstrates the correct behavior, and is a good approximation:

:$\phi=\frac\,.$

Here, $n$ is the density far from the vortex and $x=\rho/(\ell \xi)$, where $\xi=1/\sqrt$ is the healing length of the condensate.

A singly charged vortex ($\ell=1$) is in the ground state, with its energy $\epsilon_v$ given by

:$\epsilon_v=\pi n \frac\ln\left(1.464\frac\right)$

where $\,b$ is the farthest distance from the vortices considered.(To obtain an energy which is well defined it is necessary to include this boundary $b$.)

For multiply charged vortices ($\ell >1$) the energy is approximated by

:$\epsilon_v\approx \ell^2\pi n \frac\ln\left(\frac\right)$

which is greater than that of $\ell$ singly charged vortices, indicating that these multiply charged vortices are unstable to decay. Research has, however, indicated they are metastable states, so may have relatively long lifetimes.

Closely related to the creation of vortices in BECs is the generation of so-called dark solitons in one-dimensional BECs. These topological objects feature a phase gradient across their nodal plane, which stabilizes their shape even in propagation and interaction. Although solitons carry no charge and are thus prone to decay, relatively long-lived dark solitons have been produced and studied extensively.

Attractive interactions

Experiments led by Randall Hulet at Rice University from 1995 through 2000 showed that lithium condensates with attractive interactions could stably exist up to a critical atom number. Quench cooling the gas, they observed the condensate to grow, then subsequently collapse as the attraction overwhelmed the zero-point energy of the confining potential, in a burst reminiscent of a supernova, with an explosion preceded by an implosion.

Further work on attractive condensates was performed in 2000 by the JILA team, of Cornell, Wieman and coworkers. Their instrumentation now had better control so they used naturally ''attracting'' atoms of rubidium-85 (having negative atom–atom scattering length). Through Feshbach resonance involving a sweep of the magnetic field causing spin flip collisions, they lowered the characteristic, discrete energies at which rubidium bonds, making their Rb-85 atoms repulsive and creating a stable condensate. The reversible flip from attraction to repulsion stems from quantum interference among wave-like condensate atoms.

When the JILA team raised the magnetic field strength further, the condensate suddenly reverted to attraction, imploded and shrank beyond detection, then exploded, expelling about two-thirds of its 10,000 atoms. About half of the atoms in the condensate seemed to have disappeared from the experiment altogether, not seen in the cold remnant or expanding gas cloud. Carl Wieman explained that under current atomic theory this characteristic of Bose–Einstein condensate could not be explained because the energy state of an atom near absolute zero should not be enough to cause an implosion; however, subsequent mean-field theories have been proposed to explain it. Most likely they formed molecules of two rubidium atoms; energy gained by this bond imparts velocity sufficient to leave the trap without being detected.

The process of creation of molecular Bose condensate during the sweep of the magnetic field throughout the Feshbach resonance, as well as the reverse process, are described by the exactly solvable model that can explain many experimental observations.

Current research

Compared to more commonly encountered states of matter, Bose–Einstein condensates are extremely fragile. The slightest interaction with the external environment can be enough to warm them past the condensation threshold, eliminating their interesting properties and forming a normal gas.

Nevertheless, they have proven useful in exploring a wide range of questions in fundamental physics, and the years since the initial discoveries by the JILA and MIT groups have seen an increase in experimental and theoretical activity. Examples include experiments that have demonstrated interference between condensates due to wave–particle duality, the study of superfluidity and quantized vortices, the creation of bright matter wave solitons from Bose condensates confined to one dimension, and the slowing of light pulses to very low speeds using electromagnetically induced transparency. Vortices in Bose–Einstein condensates are also currently the subject of analogue gravity research, studying the possibility of modeling black holes and their related phenomena in such environments in the laboratory. Experimenters have also realized "optical lattices", where the interference pattern from overlapping lasers provides a periodic potential. These have been used to explore the transition between a superfluid and a Mott insulator, and may be useful in studying Bose–Einstein condensation in fewer than three dimensions, for example the Tonks–Girardeau gas. Further, the sensitivity of the pinning transition of strongly interacting bosons confined in a shallow one-dimensional optical lattice originally observed by Haller has been explored via a tweaking of the primary optical lattice by a secondary weaker one. Thus for a resulting weak bichromatic optical lattice, it has been found that the pinning transition is robust against the
introduction of the weaker secondary optical lattice. Studies of vortices in nonuniform Bose–Einstein condensates as well as excitatons of these systems by the application of moving repulsive or attractive obstacles, have also been undertaken. Within this context, the conditions for order and chaos in the dynamics of a trapped Bose–Einstein condensate have been explored by the application of moving blue and red-detuned laser beams via the time-dependent Gross-Pitaevskii equation.

Bose–Einstein condensates composed of a wide range of isotopes have been produced.

Cooling fermions to extremely low temperatures has created degenerate gases, subject to the Pauli exclusion principle. To exhibit Bose–Einstein condensation, the fermions must "pair up" to form bosonic compound particles (e.g. molecules or Cooper pairs). The first molecular condensates were created in November 2003 by the groups of Rudolf Grimm at the University of Innsbruck, Deborah S. Jin at the University of Colorado at Boulder and Wolfgang Ketterle at MIT. Jin quickly went on to create the first fermionic condensate, working with the same system but outside the molecular regime.

In 1999, Danish physicist Lene Hau led a team from Harvard University which slowed a beam of light to about 17 meters per second using a superfluid. Hau and her associates have since made a group of condensate atoms recoil from a light pulse such that they recorded the light's phase and amplitude, recovered by a second nearby condensate, in what they term "slow-light-mediated atomic matter-wave amplification" using Bose–Einstein condensates: details are discussed in ''Nature''.

Another current research interest is the creation of Bose–Einstein condensates in microgravity in order to use its properties for high precision atom interferometry. The first demonstration of a BEC in weightlessness was achieved in 2008 at a drop tower in Bremen, Germany by a consortium of researchers led by Ernst M. Rasel from Leibniz University Hannover. The same team demonstrated in 2017 the first creation of a Bose–Einstein condensate in space and it is also the subject of two upcoming experiments on the International Space Station.

Researchers in the new field of atomtronics use the properties of Bose–Einstein condensates in the emerging quantum technology of matter-wave circuits.

In 1970, BECs were proposed by Emmanuel David Tannenbaum for anti- stealth technology.

In 2020, researchers reported the development of superconducting BEC and that there appears to be a "smooth transition between" BEC and Bardeen–Cooper–Shrieffer regimes.

Continuous Bose–Einstein condensation

Limitations of evaporative cooling have restricted atomic BECs to "pulsed" operation, involving a highly inefficient duty cycle that discards more than 99% of atoms to reach BEC. Achieving continuous BEC has been a major open problem of experimental BEC research, driven by the same motivations as continuous optical laser development: high flux, high coherence matter waves produced continuously would enable new sensing applications.

Continuous BEC was achieved for the first time in 2022.

Dark matter

P. Sikivie and Q. Yang showed that cold dark matter axions form a Bose–Einstein condensate by thermalisation because of gravitational self-interactions. Axions have not yet been confirmed to exist. However the important search for them has been greatly enhanced with the completion of upgrades to the Axion Dark Matter Experiment (ADMX) at the University of Washington in early 2018.

In 2014, a potential dibaryon was detected at the Jülich Research Center at about 2380 MeV. The center claimed that the measurements confirm results from 2011, via a more replicable method. The particle existed for 10⁻²³ seconds and was named d*(2380). This particle is hypothesized to consist of three up and three down quarks. It is theorized that groups of d* (d-stars) could form Bose–Einstein condensates due to prevailing low temperatures in the early universe, and that BECs made of such hexaquarks with trapped electrons could behave like dark matter.

Isotopes

The effect has mainly been observed on alkaline atoms which have nuclear properties particularly suitable for working with traps. As of 2012, using ultra-low temperatures of $10^ K$ or below, Bose–Einstein condensates had been obtained for a multitude of isotopes, mainly of alkali metal, alkaline earth metal,
and lanthanide atoms (, , , , , , , , , , , , , , and ). Research was finally successful in hydrogen with the aid of the newly developed method of 'evaporative cooling'. In contrast, the superfluid state of below is not a good example, because the interaction between the atoms is too strong. Only 8% of atoms are in the ground state of the trap near absolute zero, rather than the 100% of a true condensate.

The bosonic behavior of some of these alkaline gases appears odd at first sight, because their nuclei have half-integer total spin. It arises from a subtle interplay of electronic and nuclear spins: at ultra-low temperatures and corresponding excitation energies, the half-integer total spin of the electronic shell and half-integer total spin of the nucleus are coupled by a very weak hyperfine interaction. The total spin of the atom, arising from this coupling, is an integer lower value. The chemistry of systems at room temperature is determined by the electronic properties, which is essentially fermionic, since room temperature thermal excitations have typical energies much higher than the hyperfine values.

In fiction

* In the 2016 film ''Spectral'', the US military battles mysterious enemy creatures fashioned out of Bose–Einstein condensates.
* In the 2003 novel '' Blind Lake'', scientists observe sentient life on a planet 51 light-years away using telescopes powered by Bose–Einstein condensate-based quantum computers.
* The video game franchise ''Mass Effect'' has cryonic ammunition whose flavour text describes it as being filled with Bose-Einstein condensates. Upon impact, the bullets rupture and spray super-cold liquid on the enemy.

See also

* Atom laser
* Atomic coherence
* Bose–Einstein correlations
* Bose–Einstein condensation: a network theory approach
* Bose–Einstein condensation of quasiparticles
* Bose–Einstein statistics
* Cold Atom Laboratory
* Electromagnetically induced transparency
* Fermionic condensate
* Gas in a box
* Gross–Pitaevskii equation
* Macroscopic quantum phenomena
* Macroscopic quantum self-trapping
* Slow light
* Super-heavy atom
* Superconductivity
* Superfluid film
* Superfluid helium-4
* Supersolid
* Tachyon condensation
* Timeline of low-temperature technology
* Ultracold atom
* Wiener sausage

References

Further reading

*
* ,
*
*
*
*
*
* .
*
* .
*
*
*
*
* .
*
*
*
*
* C. J. Pethick and H. Smith, ''Bose–Einstein Condensation in Dilute Gases'', Cambridge University Press, Cambridge, 2001.
* Lev P. Pitaevskii and S. Stringari, ''Bose–Einstein Condensation'', Clarendon Press, Oxford, 2003.
*
* Monique Combescot and Shiue-Yuan Shiau, "Excitons and Cooper Pairs: Two Composite Bosons in Many-Body Physics", Oxford University Press ().

External links

Bose–Einstein Condensation 2009 Conference
Bose–Einstein Condensation 2009 – Frontiers in Quantum Gases

General introduction to Bose–Einstein condensation

– for the achievement of Bose–Einstein condensation in dilute gases of alkali atoms, and for early fundamental studies of the properties of the condensates
*
Bose–Einstein condensates at JILAAtomcool at Rice UniversityAtom Optics at UQEinstein's manuscript on the Bose–Einstein condensate discovered at Leiden UniversityBose–Einstein condensate on arxiv.orgEasy BEC machine
– information on constructing a Bose–Einstein condensate machine.
Verging on absolute zero – Cosmos Online

Lecture by W Ketterle at MIT in 2001Bose–Einstein Condensation at NIST
– NIST resource on BEC

{{DEFAULTSORT:Bose-Einstein Condensate

Albert Einstein
Condensed matter physics
Exotic matter
Phases of matter
Articles containing video clips