torus group

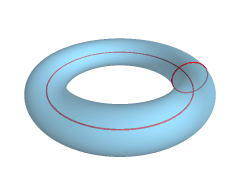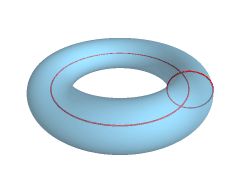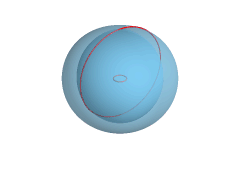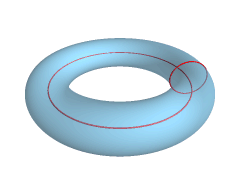
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle.

If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid.

Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses.

A torus should not be confused with a '' solid torus'', which is formed by rotating a disk, rather than a circle, around an axis. A solid torus is a torus plus the volume inside the torus. Real-world objects that approximate a ''solid torus'' include O-rings, non-inflatable lifebuoys, ring doughnuts, and bagels.

In topology, a ring torus is homeomorphic to the Cartesian product of two circles: $S^\times S^$, and the latter is taken to be the definition in that context. It is a compact 2-manifold of genus 1. The ring torus is one way to embed this space into Euclidean space, but another way to do this is the Cartesian product of the embedding of $S^$ in the plane with itself. This produces a geometric object called the Clifford torus, a surface in 4-space.

In the field of topology, a torus is any topological space that is homeomorphic to a torus. The surface of a coffee cup and a doughnut are both topological tori with genus one.

An example of a torus can be constructed by taking a rectangular strip of flexible material, for example, a rubber sheet, and joining the top edge to the bottom edge, and the left edge to the right edge, without any half-twists (compare Möbius strip).

Geometry

A torus can be defined parametrically by:
$\begin x(\theta, \varphi) &= (R + r \cos \theta) \cos\\ y(\theta, \varphi) &= (R + r \cos \theta) \sin\\ z(\theta, \varphi) &= r \sin \theta\\ \text~ \theta, \varphi \in [0,2\pi) \end$
where
*, are angles which make a full circle, so their values start and end at the same point,
* is the distance from the center of the tube to the center of the torus,
* is the radius of the tube.

Angle represents rotation around the tube, whereas represents rotation around the torus' axis of revolution. is known as the "major radius" and is known as the "minor radius". The ratio divided by is known as the "aspect ratio". The typical doughnut confectionery has an aspect ratio of about 3 to 2.

An implicit function, implicit equation in Cartesian coordinates for a torus radially symmetric about the -coordinate axis, axis is
$\left(\sqrt - R\right)^2 + z^2 = r^2,$

or the solution of , where
$f(x,y,z) = \left(\sqrt - R\right)^2 + z^2 - r^2.$

Algebraically eliminating the square root gives a quartic equation,
$\left(x^2 + y^2 + z^2 + R^2 - r^2\right)^2 = 4R^2\left(x^2+y^2\right).$

The three classes of standard tori correspond to the three possible aspect ratios between and :

*When , the surface will be the familiar ring torus or anchor ring.
* corresponds to the horn torus, which in effect is a torus with no "hole".
* describes the self-intersecting spindle torus; its inner shell is a ''lemon'' and its outer shell is an ''apple''
*When , the torus degenerates to the sphere.

When , the interior
$\left(\sqrt - R\right)^2 + z^2 < r^2$
of this torus is diffeomorphic (and, hence, homeomorphic) to a product of a Euclidean open disk and a circle. The volume of this solid torus and the surface area of its torus are easily computed using Pappus's centroid theorem, giving:
$\begin A &= \left( 2\pi r \right) \left(2 \pi R \right) = 4 \pi^2 R r \\ V &= \left ( \pi r^2 \right ) \left( 2 \pi R \right) = 2 \pi^2 R r^2. \end$

These formulas are the same as for a cylinder of length and radius , obtained from cutting the tube along the plane of a small circle, and unrolling it by straightening out (rectifying) the line running around the center of the tube. The losses in surface area and volume on the inner side of the tube exactly cancel out the gains on the outer side.

Expressing the surface area and the volume by the distance of an outermost point on the surface of the torus to the center, and the distance of an innermost point to the center (so that and ), yields
$\begin A &= 4 \pi^2 \left(\frac\right) \left(\frac\right) = \pi^2 (p+q) (p-q) \\ V &= 2 \pi^2 \left(\frac\right) \left(\frac\right)^2 = \tfrac14 \pi^2 (p+q) (p-q)^2 \end$

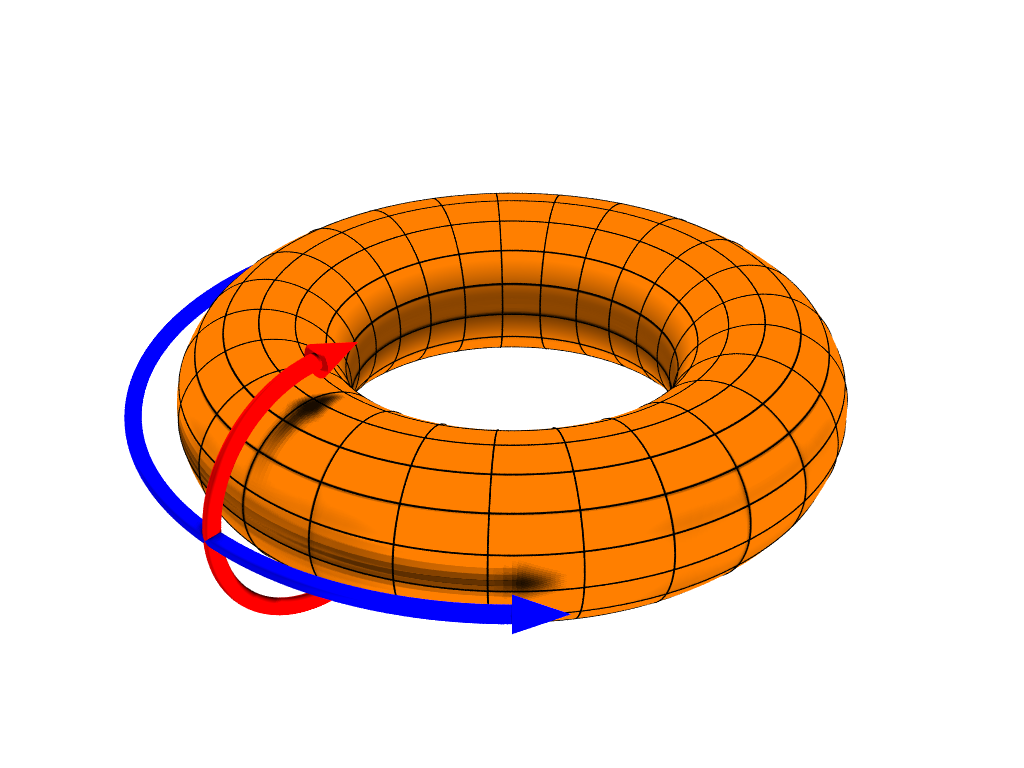
As a torus is the product of two circles, a modified version of the spherical coordinate system is sometimes used.
In traditional spherical coordinates there are three measures, , the distance from the center of the coordinate system, and and , angles measured from the center point.

As a torus has, effectively, two center points, the centerpoints of the angles are moved; measures the same angle as it does in the spherical system, but is known as the "toroidal" direction. The center point of is moved to the center of , and is known as the "poloidal" direction. These terms were first used in a discussion of the Earth's magnetic field, where "poloidal" was used to denote "the direction toward the poles".

In modern use, toroidal and poloidal are more commonly used to discuss magnetic confinement fusion devices.

Topology

Topologically, a torus is a closed surface defined as the product of two circles: ''S''¹ × ''S''¹. This can be viewed as lying in C² and is a subset of the 3-sphere ''S''³ of radius √2. This topological torus is also often called the Clifford torus. In fact, ''S''³ is filled out by a family of nested tori in this manner (with two degenerate circles), a fact which is important in the study of ''S''³ as a fiber bundle over ''S''² (the Hopf bundle).

The surface described above, given the relative topology from $\mathbb^$, is homeomorphic to a topological torus as long as it does not intersect its own axis. A particular homeomorphism is given by stereographically projecting the topological torus into $\mathbb^$ from the north pole of ''S''³.

The torus can also be described as a quotient of the Cartesian plane under the identifications
:$(x,y) \sim (x+1,y) \sim (x,y+1), \,$

or, equivalently, as the quotient of the unit square by pasting the opposite edges together, described as a fundamental polygon ''ABA''⁻¹''B''⁻¹.

The fundamental group of the torus is just the direct product of the fundamental group of the circle with itself:
:$\pi_1(\mathbb^2) = \pi_1(\mathbb^1) \times \pi_1(\mathbb^1) \cong \mathbb \times \mathbb.$

Intuitively speaking, this means that a closed path that circles the torus' "hole" (say, a circle that traces out a particular latitude) and then circles the torus' "body" (say, a circle that traces out a particular longitude) can be deformed to a path that circles the body and then the hole. So, strictly 'latitudinal' and strictly 'longitudinal' paths commute. An equivalent statement may be imagined as two shoelaces passing through each other, then unwinding, then rewinding.

If a torus is punctured and turned inside out then another torus results, with lines of latitude and longitude interchanged. This is equivalent to building a torus from a cylinder, by joining the circular ends together, in two ways: around the outside like joining two ends of a garden hose, or through the inside like rolling a sock (with the toe cut off). Additionally, if the cylinder was made by gluing two opposite sides of a rectangle together, choosing the other two sides instead will cause the same reversal of orientation.

The first homology group of the torus is isomorphic to the fundamental group (this follows from Hurewicz theorem since the fundamental group is abelian).

Two-sheeted cover

The 2-torus double-covers the 2-sphere, with four ramification points. Every conformal structure on the 2-torus can be represented as a two-sheeted cover of the 2-sphere. The points on the torus corresponding to the ramification points are the Weierstrass points. In fact, the conformal type of the torus is determined by the cross-ratio of the four points.

''n''-dimensional torus

The torus has a generalization to higher dimensions, the , often called the or for short. (This is the more typical meaning of the term "''n''-torus", the other referring to ''n'' holes or of genus ''n''.) Recalling that the torus is the product space of two circles, the ''n''-dimensional torus is the product of ''n'' circles. That is:
:$\mathbb^n = \underbrace_n.$

The standard 1-torus is just the circle: $\mathbb^=\mathbb^$. The torus discussed above is the standard 2-torus, $\mathbb^2$. And similar to the 2-torus, the ''n''-torus, $\mathbb^$ can be described as a quotient of $\mathbb^$ under integral shifts in any coordinate. That is, the ''n''-torus is $\mathbb^$ modulo the action of the integer lattice $\mathbb^$ (with the action being taken as vector addition). Equivalently, the ''n''-torus is obtained from the ''n''-dimensional hypercube by gluing the opposite faces together.

An ''n''-torus in this sense is an example of an ''n-''dimensional compact manifold. It is also an example of a compact abelian Lie group. This follows from the fact that the unit circle is a compact abelian Lie group (when identified with the unit complex numbers with multiplication). Group multiplication on the torus is then defined by coordinate-wise multiplication.

Toroidal groups play an important part in the theory of compact Lie groups. This is due in part to the fact that in any compact Lie group ''G'' one can always find a maximal torus; that is, a closed subgroup which is a torus of the largest possible dimension. Such maximal tori ''T'' have a controlling role to play in theory of connected ''G''. Toroidal groups are examples of protori, which (like tori) are compact connected abelian groups, which are not required to be manifolds.

Automorphisms of ''T'' are easily constructed from automorphisms of the lattice $\mathbb^$, which are classified by invertible integral matrices of size ''n'' with an integral inverse; these are just the integral matrices with determinant ±1. Making them act on $\mathbb^$ in the usual way, one has the typical ''toral automorphism'' on the quotient.

The fundamental group of an ''n''-torus is a free abelian group of rank ''n''. The ''k''-th homology group of an ''n''-torus is a free abelian group of rank ''n'' choose ''k''. It follows that the Euler characteristic of the ''n''-torus is 0 for all ''n''. The cohomology ring ''H''^•($\mathbb^$, Z) can be identified with the exterior algebra over the Z-module $\mathbb^$ whose generators are the duals of the ''n'' nontrivial cycles.

Configuration space

As the ''n''-torus is the ''n''-fold product of the circle, the ''n''-torus is the configuration space of ''n'' ordered, not necessarily distinct points on the circle. Symbolically, $\mathbb^= (\mathbb^)^$. The configuration space of ''unordered'', not necessarily distinct points is accordingly the orbifold $\mathbb^ / \mathbb_$, which is the quotient of the torus by the symmetric group on ''n'' letters (by permuting the coordinates).

For ''n'' = 2, the quotient is the Möbius strip, the edge corresponding to the orbifold points where the two coordinates coincide. For ''n'' = 3 this quotient may be described as a solid torus with cross-section an equilateral triangle, with a twist; equivalently, as a triangular prism whose top and bottom faces are connected with a 1/3 twist (120°): the 3-dimensional interior corresponds to the points on the 3-torus where all 3 coordinates are distinct, the 2-dimensional face corresponds to points with 2 coordinates equal and the 3rd different, while the 1-dimensional edge corresponds to points with all 3 coordinates identical.

These orbifolds have found significant applications to music theory in the work of Dmitri Tymoczko and collaborators (Felipe Posada, Michael Kolinas, et al.), being used to model musical triads.

Flat torus

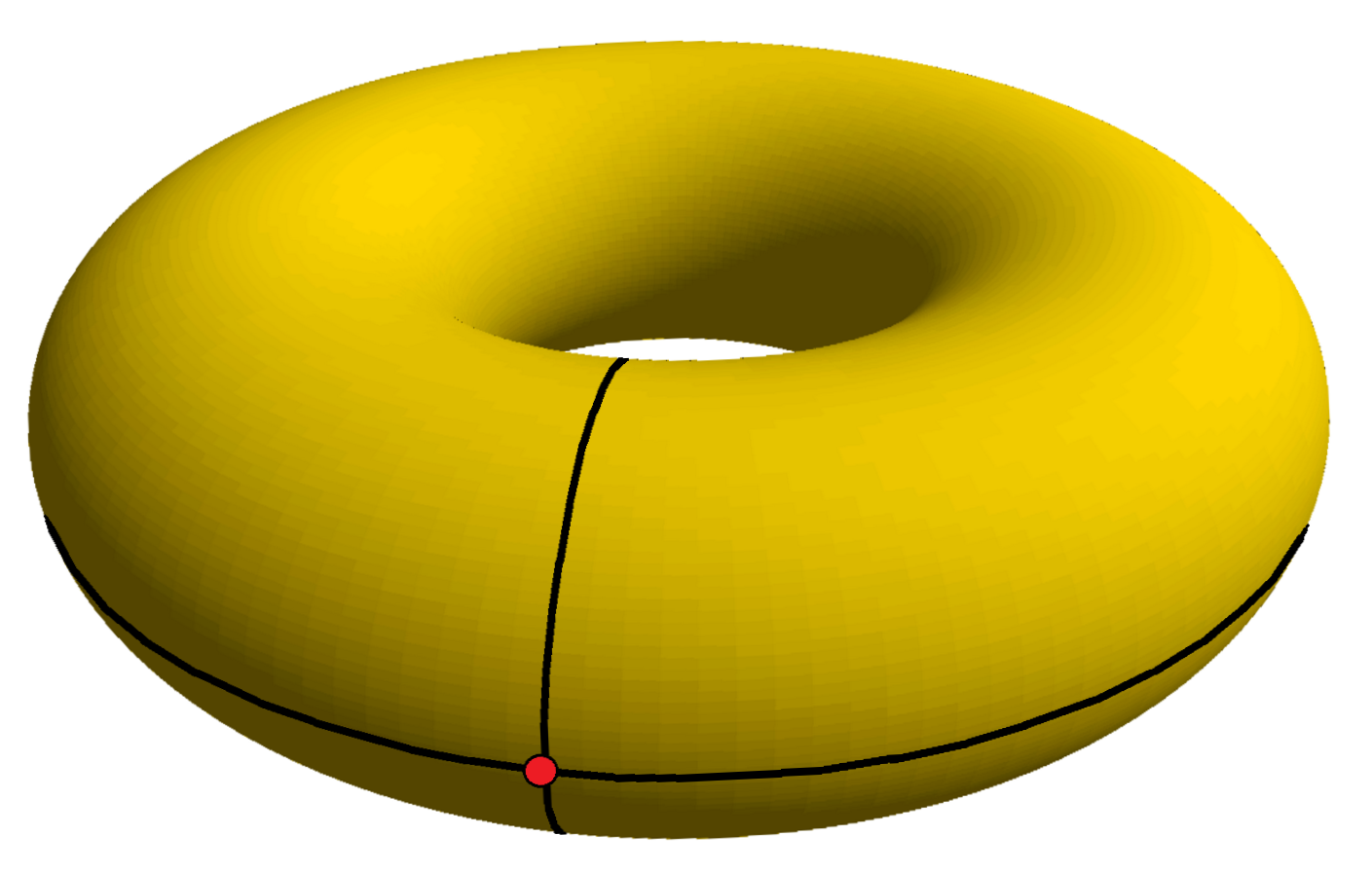
A flat torus is a torus with the metric inherited from its representation as the quotient, $\mathbb^$/L, where L is a discrete subgroup of $\mathbb^$ isomorphic to $\mathbb^$. This gives the quotient the structure of a Riemannian manifold. Perhaps the simplest example of this is when : $\mathbb^/\mathbb^$, which can also be described as the Cartesian plane under the identifications . This particular flat torus (and any uniformly scaled version of it) is known as the "square" flat torus.

This metric of the square flat torus can also be realised by specific embeddings of the familiar 2-torus into Euclidean 4-space or higher dimensions. Its surface has zero Gaussian curvature everywhere. Its surface is flat in the same sense that the surface of a cylinder is flat. In 3 dimensions, one can bend a flat sheet of paper into a cylinder without stretching the paper, but this cylinder cannot be bent into a torus without stretching the paper (unless some regularity and differentiability conditions are given up, see below).

A simple 4-dimensional Euclidean embedding of a rectangular flat torus (more general than the square one) is as follows:
:$(x,y,z,w) = (R\cos u, R\sin u, P\cos v, P\sin v)$

where ''R'' and ''P'' are positive constants determining the aspect ratio. It is diffeomorphic to a regular torus but not isometric. It can not be analytically embedded (smooth of class ) into Euclidean 3-space. Mapping it into ''3''-space requires one to stretch it, in which case it looks like a regular torus. For example, in the following map:
:$(x,y,z) = ((R+P\sin v)\cos u, (R+P\sin v)\sin u, P\cos v).$

If ''R'' and ''P'' in the above flat torus parametrization form a unit vector then ''u'', ''v'', and 0 < ''η'' < /2 parameterize the unit 3-sphere as Hopf coordinates. In particular, for certain very specific choices of a square flat torus in the 3-sphere ''S''³, where above, the torus will partition the 3-sphere into two congruent solid tori subsets with the aforesaid flat torus surface as their common boundary. One example is the torus T defined by
:$T = \left\.$

Other tori in ''S''³ having this partitioning property include the square tori of the form ''Q''⋅T, where ''Q'' is a rotation of 4-dimensional space $\mathbb^$, or in other words ''Q'' is a member of the Lie group SO(4).

It is known that there exists no ''C''² (twice continuously differentiable) embedding of a flat torus into 3-space. (The idea of the proof is to take a large sphere containing such a flat torus in its interior, and shrink the radius of the sphere until it just touches the torus for the first time. Such a point of contact must be a tangency. But that would imply that part of the torus, since it has zero curvature everywhere, must lie strictly outside the sphere, which is a contradiction.) On the other hand, according to the Nash-Kuiper theorem, which was proven in the 1950s, an isometric ''C''¹ embedding exists. This is solely an existence proof and does not provide explicit equations for such an embedding.

In April 2012, an explicit ''C''¹ (continuously differentiable) embedding of a flat torus into 3-dimensional Euclidean space $\mathbb^$ was found. It is a flat torus in the sense that as metric spaces, it is isometric to a flat square torus. It is similar in structure to a fractal as it is constructed by repeatedly corrugating an ordinary torus. Like fractals, it has no defined Gaussian curvature. However, unlike fractals, it does have defined surface normals, yielding a so-called "smooth fractal". The key to obtain the smoothness of this corrugated torus is to have the amplitudes of successive corrugations decreasing faster than their "wavelengths". (These infinitely recursive corrugations are used only for embedding into three dimensions; they are not an intrinsic feature of the flat torus.) This is the first time that any such embedding was defined by explicit equations or depicted by computer graphics.

Genus ''g'' surface

In the theory of surfaces there is another object, the "genus" ''g'' surface. Instead of the product of ''n'' circles, a genus ''g'' surface is the connected sum of ''g'' two-tori. To form a connected sum of two surfaces, remove from each the interior of a disk and "glue" the surfaces together along the boundary circles. To form the connected sum of more than two surfaces, sum two of them at a time until they are all connected. In this sense, a genus ''g'' surface resembles the surface of ''g'' doughnuts stuck together side by side, or a 2-sphere with ''g'' handles attached.

As examples, a genus zero surface (without boundary) is the two-sphere while a genus one surface (without boundary) is the ordinary torus. The surfaces of higher genus are sometimes called ''n''-holed tori (or, rarely, ''n''-fold tori). The terms double torus and triple torus are also occasionally used.

The classification theorem for surfaces states that every compact connected surface is topologically equivalent to either the sphere or the connect sum of some number of tori, disks, and real projective planes.

Toroidal polyhedra

Polyhedra with the topological type of a torus are called toroidal polyhedra, and have Euler characteristic ''V'' − ''E'' + ''F'' = 0. For any number of holes, the formula generalizes to ''V'' − ''E'' + ''F'' = 2 − 2''N'', where ''N'' is the number of holes.

The term "toroidal polyhedron" is also used for higher-genus polyhedra and for immersions of toroidal polyhedra.

Automorphisms

The homeomorphism group (or the subgroup of diffeomorphisms) of the torus is studied in geometric topology. Its mapping class group (the connected components of the homeomorphism group) is surjective onto the group $\operatorname(n,\mathbb)$ of invertible integer matrices, which can be realized as linear maps on the universal covering space $\mathbb^$ that preserve the standard lattice $\mathbb^$ (this corresponds to integer coefficients) and thus descend to the quotient.

At the level of homotopy and homology, the mapping class group can be identified as the action on the first homology (or equivalently, first cohomology, or on the fundamental group, as these are all naturally isomorphic; also the first cohomology group generates the cohomology algebra:
:$\operatorname_(\mathbb^n) = \operatorname(\pi_1(X)) = \operatorname(\mathbb^n) = \operatorname(n,\mathbb).$

Since the torus is an Eilenberg–MacLane space ''K''(''G'', 1), its homotopy equivalences, up to homotopy, can be identified with automorphisms of the fundamental group); all homotopy equivalences of the torus can be realized by homeomorphisms – every homotopy equivalence is homotopic to a homeomorphism.

Thus the short exact sequence of the mapping class group splits (an identification of the torus as the quotient of $\mathbb^$ gives a splitting, via the linear maps, as above):
:$1 \to \operatorname_0(\mathbb^n) \to \operatorname(\mathbb^n) \to \operatorname_(\mathbb^n) \to 1.$

The mapping class group of higher genus surfaces is much more complicated, and an area of active research.

Coloring a torus

The torus's chromatic number is seven, meaning every graph that can be embedded on the torus has a chromatic number of at most seven. (Since the complete graph $\mathsf$ can be embedded on the torus, and $\chi (\mathsf) = 7$, the upper bound is tight.) Equivalently, in a torus divided into regions, it is always possible to color the regions using no more than seven colors so that no neighboring regions are the same color. (Contrast with the four color theorem for the plane.)

de Bruijn torus

In combinatorial mathematics, a ''de Bruijn torus'' is an array of symbols from an alphabet (often just 0 and 1) that contains every ''m''-by-''n'' matrix exactly once. It is a torus because the edges are considered wraparound for the purpose of finding matrices. Its name comes from the De Bruijn sequence, which can be considered a special case where ''n'' is 1 (one dimension).

Cutting a torus

A solid torus of revolution can be cut by ''n'' (> 0) planes into maximally
:$\beginn+2 \\ n-1\end +\beginn \\ n-1\end = \tfrac(n^3 + 3n^2 + 8n)$
parts.

The first 11 numbers of parts, for 0 ≤ ''n'' ≤ 10 (including the case of ''n'' = 0, not covered by the above formulas), are as follows:
:1, 2, 6, 13, 24, 40, 62, 91, 128, 174, 230, ... .

See also

Notes

*''Nociones de Geometría Analítica y Álgebra Lineal'', , Author: Kozak Ana Maria, Pompeya Pastorelli Sonia, Verdanega Pedro Emilio, Editorial: McGraw-Hill, Edition 2007, 744 pages, language: Spanish
*Allen Hatcher
''Algebraic Topology''
Cambridge University Press, 2002. .
*V. V. Nikulin, I. R. Shafarevich. ''Geometries and Groups''. Springer, 1987. , .
"Tore (notion géométrique)" at ''Encyclopédie des Formes Mathématiques Remarquables''

References

External links

Creation of a torus
at cut-the-knot
"4D torus"
Fly-through cross-sections of a four-dimensional torus
"Relational Perspective Map"
Visualizing high dimensional data with flat torus

*Archived a
Ghostarchive
and th
Wayback Machine

*

{{Authority control

Surfaces