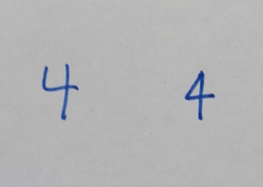|
Four Color Theorem
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubters remain. The four color theorem was proved in 1976 by Kenneth Appel and Wolfgang Haken after many false proofs and counterexamples (unlike the five color theorem, proved in the 1800s, which states that five colors are enough to color a map). To dispel any remaining doubts about the Appel–Haken proof, a simpler proof using the same ideas and still relying on computers was publi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four Colour Map Example
4 (four) is a number, numeral (linguistics), numeral and numerical digit, digit. It is the natural number following 3 and preceding 5. It is the smallest semiprime and composite number, and is tetraphobia, considered unlucky in many East Asian cultures. In mathematics Four is the smallest composite number, its proper divisors being and . Four is the sum and product of two with itself: 2 + 2 = 4 = 2 x 2, the only number b such that a + a = b = a x a, which also makes four the smallest squared prime number p^. In Knuth's up-arrow notation, , and so forth, for any number of up arrows. By consequence, four is the only square one more than a prime number, specifically 3, three. The sum of the first four prime numbers 2, two + 3, three + 5, five + 7, seven is the only sum of four consecutive prime numbers that yields an Parity (mathematics), odd prime number, 17 (number), seventeen, which is the fourth super-prime. Four lies between the first proper pair of twin primes, 3, three and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angola
, national_anthem = " Angola Avante"() , image_map = , map_caption = , capital = Luanda , religion = , religion_year = 2020 , religion_ref = , coordinates = , largest_city = capital , official_languages = Portuguese , languages2_type = National languages , languages2 = , ethnic_groups = , ethnic_groups_ref = , ethnic_groups_year = 2000 , demonym = , government_type = Unitary dominant-party presidential republic , leader_title1 = President , leader_name1 = João Lourenço , leader_title2 = Vice President , leader_name2 = Esperança da CostaInvestidura do Pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undirected Graph
In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called '' vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by '' edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four Colour Planar Graph
4 (four) is a number, numeral and digit. It is the natural number following 3 and preceding 5. It is the smallest semiprime and composite number, and is considered unlucky in many East Asian cultures. In mathematics Four is the smallest composite number, its proper divisors being and . Four is the sum and product of two with itself: 2 + 2 = 4 = 2 x 2, the only number b such that a + a = b = a x a, which also makes four the smallest squared prime number p^. In Knuth's up-arrow notation, , and so forth, for any number of up arrows. By consequence, four is the only square one more than a prime number, specifically three. The sum of the first four prime numbers two + three + five + seven is the only sum of four consecutive prime numbers that yields an odd prime number, seventeen, which is the fourth super-prime. Four lies between the first proper pair of twin primes, three and five, which are the first two Fermat primes, like seventeen, which is the third. On the other h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalizations
A generalization is a form of abstraction whereby common properties of specific instances are formulated as general concepts or claims. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements (thus creating a conceptual model). As such, they are the essential basis of all valid deductive inferences (particularly in logic, mathematics and science), where the process of verification is necessary to determine whether a generalization holds true for any given situation. Generalization can also be used to refer to the process of identifying the parts of a whole, as belonging to the whole. The parts, which might be unrelated when left on their own, may be brought together as a group, hence belonging to the whole by establishing a common relation between them. However, the parts cannot be generalized into a whole—until a common relation is established among ''all'' parts. This does not mean that the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genus (mathematics)
In mathematics, genus (plural genera) has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1. Topology Orientable surfaces The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it. Alternatively, it can be defined in terms of the Euler characteristic ''χ'', via the relationship ''χ'' = 2 − 2''g'' for closed surfaces, where ''g'' is the genus. For surfaces with ''b'' boundary components, the equation reads ''χ'' = 2 − 2''g'' − ''b''. In layman's terms, it's the number of "holes" an object has ("holes" interpreted in the sense of doughnut holes; a hollow sphere would be considered as having zero holes in this sense). A torus has 1 such h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a '' solid torus'', which is formed by r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4CT Inadequacy Explanation
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubters remain. The four color theorem was proved in 1976 by Kenneth Appel and Wolfgang Haken after many false proofs and counterexamples (unlike the five color theorem, proved in the 1800s, which states that five colors are enough to color a map). To dispel any remaining doubts about the Appel–Haken proof, a simpler proof using the same ideas and still relying on computers was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4CT Inadequacy Example
In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. ''Adjacent'' means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet. It was the first major theorem to be computer-assisted proof#Theorems proved with the help of computer programs, proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was Non-surveyable proof, infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubters remain. The four color theorem was proved in 1976 by Kenneth Appel and Wolfgang Haken after many false proofs and counterexamples (unlike the five color theorem, proved in the 1800s, which states that five colors are enough to color a map). To dispel any remaining doubts about the App ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
United States
The United States of America (U.S.A. or USA), commonly known as the United States (U.S. or US) or America, is a country primarily located in North America. It consists of 50 states, a federal district, five major unincorporated territories, nine Minor Outlying Islands, and 326 Indian reservations. The United States is also in free association with three Pacific Island sovereign states: the Federated States of Micronesia, the Marshall Islands, and the Republic of Palau. It is the world's third-largest country by both land and total area. It shares land borders with Canada to its north and with Mexico to its south and has maritime borders with the Bahamas, Cuba, Russia, and other nations. With a population of over 333 million, it is the most populous country in the Americas and the third most populous in the world. The national capital of the United States is Washington, D.C. and its most populous city and principal financial center is New York City. Paleo-Americ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alaska
Alaska ( ; russian: Аляска, Alyaska; ale, Alax̂sxax̂; ; ems, Alas'kaaq; Yup'ik: ''Alaskaq''; tli, Anáaski) is a state located in the Western United States on the northwest extremity of North America. A semi-exclave of the U.S., it borders the Canadian province of British Columbia and the Yukon territory to the east; it also shares a maritime border with the Russian Federation's Chukotka Autonomous Okrug to the west, just across the Bering Strait. To the north are the Chukchi and Beaufort Seas of the Arctic Ocean, while the Pacific Ocean lies to the south and southwest. Alaska is by far the largest U.S. state by area, comprising more total area than the next three largest states (Texas, California, and Montana) combined. It represents the seventh-largest subnational division in the world. It is the third-least populous and the most sparsely populated state, but by far the continent's most populous territory located mostly north of the 60th parallel, with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
