superlattice on:
[Wikipedia]
[Google]
[Amazon]
A superlattice is a periodic structure of layers of two (or more) materials. Typically, the thickness of one layer is several
 Semiconductor materials, which are used to fabricate the superlattice structures, may be divided by the element groups, IV, III-V and II-VI. While group III-V semiconductors (especially GaAs/AlxGa1−xAs) have been extensively studied, group IV heterostructures such as the SixGe1−x system are much more difficult to realize because of the large lattice mismatch. Nevertheless, the strain modification of the subband structures is interesting in these quantum structures and has attracted much attention.
In the GaAs/AlAs system both the difference in lattice constant between GaAs and AlAs and the difference of their thermal expansion coefficient are small. Thus, the remaining strain at room temperature can be minimized after cooling from epitaxial growth temperatures. The first compositional superlattice was realized using the GaAs/AlxGa1−xAs material system.
A
Semiconductor materials, which are used to fabricate the superlattice structures, may be divided by the element groups, IV, III-V and II-VI. While group III-V semiconductors (especially GaAs/AlxGa1−xAs) have been extensively studied, group IV heterostructures such as the SixGe1−x system are much more difficult to realize because of the large lattice mismatch. Nevertheless, the strain modification of the subband structures is interesting in these quantum structures and has attracted much attention.
In the GaAs/AlAs system both the difference in lattice constant between GaAs and AlAs and the difference of their thermal expansion coefficient are small. Thus, the remaining strain at room temperature can be minimized after cooling from epitaxial growth temperatures. The first compositional superlattice was realized using the GaAs/AlxGa1−xAs material system.
A

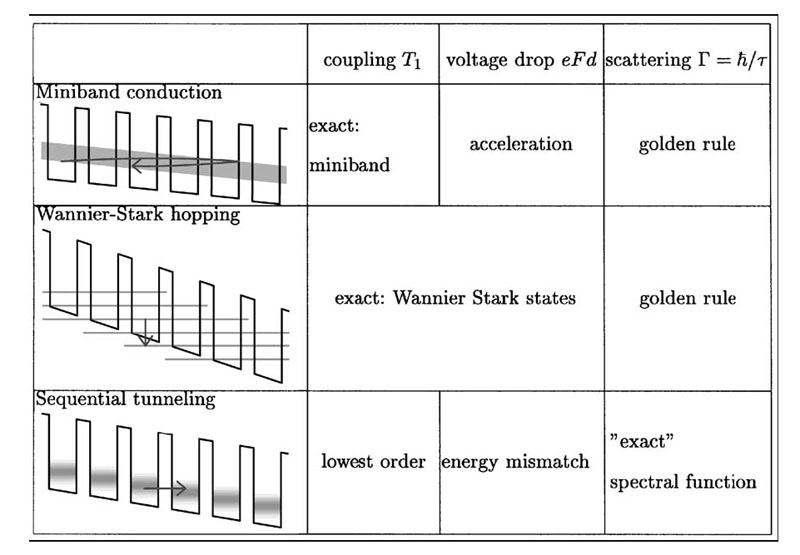 The motion of charge carriers in a superlattice is different from that in the individual layers:
The motion of charge carriers in a superlattice is different from that in the individual layers:
*C. Hamaguchi, ''"Basic Semiconductor Physics"'', Springer (2001). * *
nanometer
330px, Different lengths as in respect to the Molecule">molecular scale.
The nanometre (international spelling as used by the International Bureau of Weights and Measures; SI symbol: nm), or nanometer (American spelling
Despite the va ...
s. It can also refer to a lower-dimensional structure such as an array of quantum dot
Quantum dots (QDs) or semiconductor nanocrystals are semiconductor particles a few nanometres in size with optical and electronic properties that differ from those of larger particles via quantum mechanical effects. They are a central topic i ...
s or quantum well
A quantum well is a potential well with only discrete energy values.
The classic model used to demonstrate a quantum well is to confine particles, which were initially free to move in three dimensions, to two dimensions, by forcing them to occup ...
s.
Discovery
Superlattices were discovered early in 1925 by Johansson and Linde after the studies ongold
Gold is a chemical element; it has chemical symbol Au (from Latin ) and atomic number 79. In its pure form, it is a brightness, bright, slightly orange-yellow, dense, soft, malleable, and ductile metal. Chemically, gold is a transition metal ...
–copper
Copper is a chemical element; it has symbol Cu (from Latin ) and atomic number 29. It is a soft, malleable, and ductile metal with very high thermal and electrical conductivity. A freshly exposed surface of pure copper has a pinkish-orang ...
and palladium
Palladium is a chemical element; it has symbol Pd and atomic number 46. It is a rare and lustrous silvery-white metal discovered in 1802 by the English chemist William Hyde Wollaston. He named it after the asteroid Pallas (formally 2 Pallas), ...
–copper systems through their special X-ray diffraction patterns. Further experimental observations and theoretical modifications on the field were done by Bradley and Jay, Gorsky, Borelius, Dehlinger and Graf, Bragg and Williams and Bethe. Theories were based on the transition of arrangement of atoms in crystal lattices from disordered state to an ordered state.
Mechanical properties
J.S. Koehler theoretically predicted that by using alternate (nano-)layers of materials with high and low elastic constants, shearing resistance is improved by up to 100 times as the Frank–Read source ofdislocation
In materials science, a dislocation or Taylor's dislocation is a linear crystallographic defect or irregularity within a crystal structure that contains an abrupt change in the arrangement of atoms. The movement of dislocations allow atoms to sli ...
s cannot operate in the nanolayers.
The increased mechanical hardness
In materials science, hardness (antonym: softness) is a measure of the resistance to plastic deformation, such as an indentation (over an area) or a scratch (linear), induced mechanically either by Pressing (metalworking), pressing or abrasion ...
of such superlattice materials was confirmed firstly by Lehoczky in 1978 on Al-Cu and Al-Ag, and later on by several others, such as Barnett and Sproul on hard PVD coatings.
Semiconductor properties
If the superlattice is made of two semiconductor materials with differentband gap
In solid-state physics and solid-state chemistry, a band gap, also called a bandgap or energy gap, is an energy range in a solid where no electronic states exist. In graphs of the electronic band structure of solids, the band gap refers to t ...
s, each quantum well
A quantum well is a potential well with only discrete energy values.
The classic model used to demonstrate a quantum well is to confine particles, which were initially free to move in three dimensions, to two dimensions, by forcing them to occup ...
sets up new selection rule
In physics and chemistry, a selection rule, or transition rule, formally constrains the possible transitions of a system from one quantum state to another. Selection rules have been derived for electromagnetic transitions in molecules, in atoms, in ...
s that affect the conditions for charges to flow through the structure. The two different semiconductor materials are deposited alternately on each other to form a periodic structure in the growth direction. Since the 1970 proposal of synthetic superlattices by Esaki and Tsu, advances in the physics of such ultra-fine semiconductors, presently called quantum structures, have been made. The concept of quantum confinement
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy (kinetic energy in the case of a gravitational potential well) because it is captu ...
has led to the observation of quantum size effects in isolated quantum well heterostructures and is closely related to superlattices through the tunneling phenomena. Therefore, these two ideas are often discussed on the same physical basis, but each has different physics useful for applications in electric and optical devices.
Semiconductor superlattice types
Superlattice miniband structures depend on theheterostructure
A heterojunction is an interface between two layers or regions of dissimilar semiconductors. These semiconducting materials have unequal band gaps as opposed to a homojunction. It is often advantageous to engineer the electronic energy bands in m ...
type, either ''type I'', ''type II'' or ''type III''. For type I the bottom of the conduction band
In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level, and thus determine the electrical conductivity of the solid. In nonmetals, the valence band is the highest range of electron energies in ...
and the top of the valence subband are formed in the same semiconductor layer. In type II the conduction and valence subbands are staggered in both real and reciprocal space
Reciprocal lattice is a concept associated with solids with translational symmetry which plays a major role in many areas such as X-ray diffraction, X-ray and Electron diffraction, electron diffraction as well as the Electronic band structure, e ...
, so that electrons and holes are confined in different layers. Type III superlattices involve semimetal
A semimetal is a material with a small energy overlap between the bottom of the Electrical conduction, conduction Electronic band structure, band and the top of the valence band, but they do not overlap in momentum space. According to Band theory ...
material, such as HgTe/ CdTe. Although the bottom of the conduction subband and the top of the valence subband are formed in the same semiconductor layer in Type III superlattice, which is similar with Type I superlattice, the band gap of Type III superlattices can be continuously adjusted from semiconductor to zero band gap material and to semimetal with negative band gap.
Another class of quasiperiodic superlattices is named after Fibonacci
Leonardo Bonacci ( – ), commonly known as Fibonacci, was an Italians, Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages".
The name he is commonly called, ''Fibonacci ...
. A Fibonacci superlattice can be viewed as a one-dimensional quasicrystal
A quasiperiodicity, quasiperiodic crystal, or quasicrystal, is a structure that is Order and disorder (physics), ordered but not Bravais lattice, periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks trans ...
, where either electron hopping transfer or on-site energy takes two values arranged in a Fibonacci sequence
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many w ...
.
Semiconductor materials
graphene
Graphene () is a carbon allotrope consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice, honeycomb planar nanostructure. The name "graphene" is derived from "graphite" and the suffix -ene, indicating ...
/boron nitride
Boron nitride is a thermally and chemically resistant refractory compound of boron and nitrogen with the chemical formula B N. It exists in various crystalline forms that are isoelectronic to a similarly structured carbon lattice. The hexago ...
system forms a semiconductor superlattice once the two crystals are aligned. Its charge carriers move perpendicular to the electric field, with little energy dissipation. h-BN has a hexagonal
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon is d ...
structure similar to graphene's. The superlattice has broken inversion symmetry. Locally, topological currents are comparable in strength to the applied current, indicating large valley-Hall angles.
Production
Superlattices can be produced using various techniques, but the most common aremolecular-beam epitaxy
Molecular-beam epitaxy (MBE) is an epitaxy method for thin-film deposition of single crystals. MBE is widely used in the manufacture of semiconductor devices, including transistors. MBE is used to make diodes and MOSFETs (MOS field-effect transis ...
(MBE) and sputtering
In physics, sputtering is a phenomenon in which microscopic particles of a solid material are ejected from its surface, after the material is itself bombarded by energetic particles of a plasma or gas. It occurs naturally in outer space, and c ...
. With these methods, layers can be produced with thicknesses of only a few atomic spacings. An example of specifying a superlattice is []20. It describes a bi-layer of 20Å of Iron (Fe) and 30Å of Vanadium (V) repeated 20 times, thus yielding a total thickness of 1000Å or 100 nm. The MBE technology as a means of fabricating semiconductor superlattices is of primary importance. In addition to the MBE technology, metal-organic chemical vapor deposition (MO-CVD) has contributed to the development of superconductor superlattices, which are composed of quaternary III-V compound semiconductors like InGaAsP alloys. Newer techniques include a combination of gas source handling with ultrahigh vacuum (UHV) technologies such as metal-organic molecules as source materials and gas-source MBE using hybrid gases such as arsine () and phosphine () have been developed.
Generally speaking MBE is a method of using three temperatures in binary systems, e.g., the substrate temperature, the source material temperature of the group III and the group V elements in the case of III-V compounds.
The structural quality of the produced superlattices can be verified by means of X-ray diffraction
X-ray diffraction is a generic term for phenomena associated with changes in the direction of X-ray beams due to interactions with the electrons around atoms. It occurs due to elastic scattering, when there is no change in the energy of the waves. ...
or neutron diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material. A sample to be examined is placed in a beam of Neutron temperature, thermal or ...
spectra which contain characteristic satellite peaks. Other effects associated with the alternating layering are: giant magnetoresistance
Giant magnetoresistance (GMR) is a quantum mechanics, quantum mechanical magnetoresistance effect observed in multilayers composed of alternating ferromagnetic and non-magnetic conductive layers. The 2007 Nobel Prize in Physics was awarded to Alb ...
, tunable reflectivity for X-ray and neutron mirrors, neutron spin polarization
In particle physics, spin polarization is the degree to which the spin, i.e., the intrinsic angular momentum of elementary particles, is aligned with a given direction. This property may pertain to the spin, hence to the magnetic moment, of co ...
, and changes in elastic and acoustic properties. Depending on the nature of its components, a superlattice may be called ''magnetic'', ''optical'' or ''semiconducting''.

Miniband structure
The schematic structure of a periodic superlattice is shown below, where A and B are two semiconductor materials of respective layer thickness ''a'' and ''b'' (period: ). When ''a'' and ''b'' are not too small compared with the interatomic spacing, an adequate approximation is obtained by replacing these fast varying potentials by an effective potential derived from the band structure of the original bulk semiconductors. It is straightforward to solve 1D Schrödinger equations in each of the individual layers, whose solutions are linear combinations of real or imaginary exponentials. For a large barrier thickness, tunneling is a weak perturbation with regard to the uncoupled dispersionless states, which are fully confined as well. In this case the dispersion relation , periodic over with over by virtue of the Bloch theorem, is fully sinusoidal: : and the effective mass changes sign for : : In the case of minibands, this sinusoidal character is no longer preserved. Only high up in the miniband (for wavevectors well beyond ) is the top actually 'sensed' and does the effective mass change sign. The shape of the miniband dispersion influences miniband transport profoundly and accurate dispersion relation calculations are required given wide minibands. The condition for observing single miniband transport is the absence of interminiband transfer by any process. The thermal quantum ''kBT'' should be much smaller than the energy difference between the first and second miniband, even in the presence of the applied electric field.Bloch states
For an ideal superlattice a complete set ofeigenstates
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system re ...
states can be constructed by products of plane waves and a ''z''-dependent function which satisfies the eigenvalue equation
:.
As and are periodic functions with the superlattice period ''d'', the eigenstates are Bloch state with energy . Within first-order perturbation theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle ...
in k2, one obtains the energy
:.
Now, will exhibit a larger probability in the well, so that it seems reasonable to replace the second term by
:
where is the effective mass of the quantum well.
Wannier functions
By definition the Bloch functions are delocalized over the whole superlattice. This may provide difficulties if electric fields are applied or effects due to the superlattice's finite length are considered. Therefore, it is often helpful to use different sets of basis states that are better localized. A tempting choice would be the use of eigenstates of single quantum wells. Nevertheless, such a choice has a severe shortcoming: the corresponding states are solutions of two differentHamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
s, each neglecting the presence of the other well. Thus these states are not orthogonal, creating complications. Typically, the coupling is estimated by the transfer Hamiltonian within this approach. For these reasons, it is more convenient to use the set of Wannier function
The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier in 1937. Wannier functions are the localized molecular orbitals of crystalline systems.
The Wannier functions f ...
s.
Wannier–Stark ladder
Applying an electric field ''F'' to the superlattice structure causes the Hamiltonian to exhibit an additional scalar potential ''eφ''(''z'') = −''eFz'' that destroys the translational invariance. In this case, given an eigenstate with wavefunction and energy , then the set of states corresponding to wavefunctions are eigenstates of the Hamiltonian with energies ''E''''j'' = ''E''0 − ''jeFd''. These states are equally spaced both in energy and real space and form the so-called ''Wannier–Stark ladder''. The potential is not bounded for the infinite crystal, which implies a continuous energy spectrum. Nevertheless, the characteristic energy spectrum of these Wannier–Stark ladders could be resolved experimentally.Transport
 The motion of charge carriers in a superlattice is different from that in the individual layers:
The motion of charge carriers in a superlattice is different from that in the individual layers: mobility
Mobility may refer to:
Social sciences and humanities
* Economic mobility, ability of individuals or families to improve their economic status
* Geographic mobility, the measure of how populations and goods move over time
* Mobilities, a conte ...
of charge carriers can be enhanced, which is beneficial for high-frequency devices, and specific optical properties are used in semiconductor laser
The laser diode chip removed and placed on the eye of a needle for scale
A laser diode (LD, also injection laser diode or ILD or semiconductor laser or diode laser) is a semiconductor device similar to a light-emitting diode in which a diode p ...
s.
If an external bias is applied to a conductor, such as a metal or a semiconductor, typically an electric current is generated. The magnitude of this current is determined by the band structure of the material, scattering processes, the applied field strength and the equilibrium carrier distribution of the conductor.
A particular case of superlattices called superstripes are made of superconducting units separated by spacers. In each miniband the superconducting order parameter, called the superconducting gap, takes different values, producing a multi-gap, or two-gap or multiband superconductivity.
Recently, Felix and Pereira investigated the thermal transport by phonons in periodic and quasiperiodic superlattices of graphene-hBN according to the Fibonacci sequence. They reported that the contribution of coherent thermal transport (phonons like-wave) was suppressed as quasiperiodicity increased.
Other dimensionalities
Soon after two-dimensional electron gases (2DEG
A two-dimensional electron gas (2DEG) is a scientific model in solid-state physics. It is an Fermi gas, electron gas that is free to move in two dimensions, but tightly confined in the third. This tight confinement leads to quantized energy levels ...
) had become commonly available for experiments, research groups attempted to create structures that could be called 2D artificial crystals. The idea is to subject the electrons confined to an interface between two semiconductors (i.e. along ''z''-direction) to an additional modulation potential . Contrary to the classical superlattices (1D/3D, that is 1D modulation of electrons in 3D bulk) described above, this is typically achieved by treating the heterostructure surface: depositing a suitably patterned metallic gate or etching. If the amplitude of ''V''(''x'',''y'') is large ( as an example) compared to the Fermi level, , the electrons in the superlattice should behave similarly to electrons in an atomic crystal with square lattice (in the example, these "atoms" would be located at positions () where ''n'',''m'' are integers).
The difference is in the length and energy scales. Lattice constants of atomic crystals are of the order of 1Å while those of superlattices (''a'') are several hundreds or thousands larger as dictated by technological limits (e.g. electron-beam lithography used for the patterning of the heterostructure surface). Energies are correspondingly smaller in superlattices. Using the simple quantum-mechanically confined-particle model suggests . This relation is only a rough guide and actual calculations with currently topical graphene
Graphene () is a carbon allotrope consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice, honeycomb planar nanostructure. The name "graphene" is derived from "graphite" and the suffix -ene, indicating ...
(a natural atomic crystal) and artificial graphene (superlattice) show that characteristic band widths are of the order of 1 eV and 10 meV, respectively. In the regime of weak modulation (), phenomena like commensurability oscillations or fractal energy spectra ( Hofstadter butterfly) occur.
Artificial two-dimensional crystals can be viewed as a 2D/2D case (2D modulation of a 2D system) and other combinations are experimentally available: an array of quantum wires (1D/2D) or 3D/3D photonic crystal
A photonic crystal is an optical nanostructure in which the refractive index changes periodically. This affects the propagation of light in the same way that the structure of Crystal structure, natural crystals gives rise to X-ray crystallograp ...
s.
Applications
The superlattice of palladium-copper system is used in high performance alloys to enable a higher electrical conductivity, which is favored by the ordered structure. Further alloying elements likesilver
Silver is a chemical element; it has Symbol (chemistry), symbol Ag () and atomic number 47. A soft, whitish-gray, lustrous transition metal, it exhibits the highest electrical conductivity, thermal conductivity, and reflectivity of any metal. ...
, rhenium
Rhenium is a chemical element; it has symbol Re and atomic number 75. It is a silvery-gray, heavy, third-row transition metal in group 7 of the periodic table. With an estimated average concentration of 1 part per billion (ppb), rhenium is one ...
, rhodium
Rhodium is a chemical element; it has symbol Rh and atomic number 45. It is a very rare, silvery-white, hard, corrosion-resistant transition metal. It is a noble metal and a member of the platinum group. It has only one naturally occurring isot ...
and ruthenium
Ruthenium is a chemical element; it has symbol Ru and atomic number 44. It is a rare transition metal belonging to the platinum group of the periodic table. Like the other metals of the platinum group, ruthenium is unreactive to most chem ...
are added for better mechanical strength and high temperature stability. This alloy is used for probe needles in probe card
A probe card (commonly referred to as a DUT board) is used in automated integrated circuit testing. It is an interface between an electronic test system and a semiconductor Wafer (electronics), wafer.
Use and manufacture
A probe card or DUT b ...
s.
See also
* Cu-Pt type ordering in III-V semiconductor * Tube-based nanostructures *Wannier function
The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier in 1937. Wannier functions are the localized molecular orbitals of crystalline systems.
The Wannier functions f ...
References
*H.T. Grahn, ''"Semiconductor Superlattices"'', World Scientific (1995). * *Morten Jagd Christensen, ''"Epitaxy, Thin Films and Superlattices"'', Risø National Laboratory, (1997).*C. Hamaguchi, ''"Basic Semiconductor Physics"'', Springer (2001). * *
Further reading
* {{Authority control Condensed matter physics Spintronics