|
Fibonacci
Fibonacci (; also , ; – ), also known as Leonardo Bonacci, Leonardo of Pisa, or Leonardo Bigollo Pisano ('Leonardo the Traveller from Pisa'), was an Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages". The name he is commonly called, ''Fibonacci'', was made up in 1838 by the Franco-Italian historian Guillaume Libri and is short for ('son of Bonacci'). However, even earlier in 1506 a notary of the Holy Roman Empire, Perizolo mentions Leonardo as "Lionardo Fibonacci". Fibonacci popularized the Indo–Arabic numeral system in the Western world primarily through his composition in 1202 of '' Liber Abaci'' (''Book of Calculation''). He also introduced Europe to the sequence of Fibonacci numbers, which he used as an example in ''Liber Abaci''. Biography Fibonacci was born around 1170 to Guglielmo, an Italian merchant and customs official. Guglielmo directed a trading post in Bugia (Béjaïa) in mode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Number
In mathematics, the Fibonacci numbers, commonly denoted , form a integer sequence, sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the first few values in the sequence are: :0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. The Fibonacci numbers were first described in Indian mathematics, as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, later known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book ''Liber Abaci''. Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the ''Fibonacci Quarterly''. Applications of Fibonacci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liber Abaci
''Liber Abaci'' (also spelled as ''Liber Abbaci''; "The Book of Calculation") is a historic 1202 Latin manuscript on arithmetic by Leonardo of Pisa, posthumously known as Fibonacci. ''Liber Abaci'' was among the first Western books to describe the Hindu–Arabic numeral system and to use symbols resembling modern "Arabic numerals". By addressing the applications of both commercial tradesmen and mathematicians, it promoted the superiority of the system, and the use of these glyphs. Although the book's title has also been translated as "The Book of the Abacus", writes that this is an error: the intent of the book is to describe methods of doing calculations without aid of an abacus, and as confirms, for centuries after its publication the algorismists (followers of the style of calculation demonstrated in ''Liber Abaci'') remained in conflict with the abacists (traditionalists who continued to use the abacus in conjunction with Roman numerals). The historian of mathematics C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formulas For Generating Pythagorean Triples
Besides Euclid's formula, many other formulas for generating Pythagorean triples have been developed. Euclid's, Pythagoras', and Plato's formulas Euclid's, Pythagoras' and Plato's formulas for calculating triples have been described here: The methods below appear in various sources, often without attribution as to their origin. Fibonacci's method Leonardo of Pisa () described this method for generating primitive triples using the sequence of consecutive odd integers 1,3,5,7,9,11,\ldots and the fact that the sum of the first n terms of this sequence is n^2. If k is the n-th member of this sequence then n=(k+1)/2. Choose any odd square number k from this sequence (k=a^2) and let this square be the n-th term of the sequence. Also, let b^2 be the sum of the previous n-1 terms, and let c^2 be the sum of all n terms. Then we have established that a^2+b^2=c^2 and we have generated the primitive triple 'a, b, c'' This method produces an infinite number of primitive triples, but not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greedy Algorithm For Egyptian Fractions
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of distinct unit fractions, such as . As the name indicates, these representations have been used as long ago as ancient Egypt, but the first published systematic method for constructing such expansions was described in 1202 in the ''Liber Abaci'' of Leonardo of Pisa (Fibonacci). It is called a greedy algorithm because at each step the algorithm chooses greedily the largest possible unit fraction that can be used in any representation of the remaining fraction. Fibonacci actually lists several different methods for constructing Egyptian fraction representations. He includes the greedy method as a last resort for situations when several simpler methods fail; see Egyptian fraction for a more detailed listing of these methods. As Salzer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Béjaïa
Béjaïa (; ; ar, بجاية, Latn, ar, Bijāya, ; kab, Bgayet, Vgayet), formerly Bougie and Bugia, is a Mediterranean port city and commune on the Gulf of Béjaïa in Algeria; it is the capital of Béjaïa Province, Kabylia. Béjaïa is the largest principally Kabyle-speaking city in the region of Kabylia, Algeria. Geography The town is overlooked by the mountain ', whose profile is said to resemble a sleeping woman. Other nearby scenic spots include the ''Aiguades'' beach and the '' Pic des Singes'' (Peak of the Monkeys); the latter site is a habitat for the endangered Barbary macaque, which prehistorically had a much broader distribution than at present. All three of these geographic features are located in the Gouraya National Park. The Soummam river runs past the town. Under French rule, it was known under various European names, such as Budschaja in German, Bugia in Italian, and Bougie in French. The French and Italian versions, due to the town's wax trad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hammadid Empire
The Hammadid dynasty () was a branch of the Sanhaja Berber dynasty that ruled an area roughly corresponding to north-eastern modern Algeria between 1008 and 1152. The state reached its peak under Nasir ibn Alnas during which it was briefly the most important state in Northwest Africa. Its realm was conquered by the Almohad Caliphate. The Hammadid dynasty's first capital was at Qalaat Beni Hammad. It was founded in 1007, and is now a UNESCO World Heritage Site. When the area was sacked by the Banu Hilal tribe, the Hammadids moved their capital to Béjaïa in 1090. History Establishment In 987 and 989, al-Mansur ibn Buluggin, the emir of the Berber Zirid dynasty, appointed his uncle Hammad ibn Buluggin as governor of Ashir and western Zirid lands. Hammad subsequently defended the territory against Zenata incursions and was granted additional lands by al-Mansur's successor Badis ibn Mansur. In 1007 and 1008, forces under Hammad left Ashir and built a new citadel-capital, Qalaa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hindu–Arabic Numeral System
The Hindu–Arabic numeral system or Indo-Arabic numeral system Audun HolmeGeometry: Our Cultural Heritage 2000 (also called the Hindu numeral system or Arabic numeral system) is a positional decimal numeral system, and is the most common system for the symbolic representation of numbers in the world. It was invented between the 1st and 4th centuries by Indian mathematicians. The system was adopted in Arabic mathematics by the 9th century. It became more widely known through the writings of the Persian mathematician Al-Khwārizmī: "Historians have speculated on al-Khwarizmi's native language. Since he was born in a former Persian province, he may have spoken the Persian language. It is also possible that he spoke Khwarezmian, a language of the region that is now extinct." (''On the Calculation with Hindu Numerals'', ) and Arab mathematician Al-Kindi (''On the Use of the Hindu Numerals'', ). The system had spread to medieval Europe by the High Middle Ages. The system is ba ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Of Palermo
John of Palermo () was a translator of mathematical works from Arabic to Latin who lived in Palermo, Sicily. He worked in the court of Emperor Frederick II. It is not known if he was an Arab or a Sicilian. John had been introduced into the court of Frederick II through the mathematician Domenico Ispano. John is mentioned by Leonardo Fibonacci in his ''Liber quadratorum'' (1225) and several problems from Arab texts by Omar Khayyam were posed to Fibonacci. Some court documents mention a Johannes de Panormo who is thought to be the same person. John translated an Arab manuscript, possibly by Ibn al-Haytham Ḥasan Ibn al-Haytham, Latinized as Alhazen (; full name ; ), was a medieval mathematician, astronomer, and physicist of the Islamic Golden Age from present-day Iraq.For the description of his main fields, see e.g. ("He is one of the prin ..., on the parabola into Latin as the ''De duabus lineis semper approximantibus sibi invicem et nunquam concurrentibus''. John as noted ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Congruum
In number theory, a congruum (plural ''congrua'') is the difference between successive square numbers in an arithmetic progression of three squares. That is, if x^2, y^2, and z^2 (for integers x, y, and z) are three square numbers that are equally spaced apart from each other, then the spacing between them, z^2-y^2=y^2-x^2, is called a congruum. The congruum problem is the problem of finding squares in arithmetic progression and their associated congrua. It can be formalized as a Diophantine equation: find integers x, y, and z such that y^2 - x^2 = z^2 - y^2. When this equation is satisfied, both sides of the equation equal the congruum. Fibonacci solved the congruum problem by finding a parameterized formula for generating all congrua, together with their associated arithmetic progressions. According to this formula, each congruum is four times the area of a Pythagorean triangle. Congrua are also closely connected with congruent numbers: every congruum is a congruent number, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Italians
, flag = , flag_caption = Flag of Italy, The national flag of Italy , population = , regions = Italy 55,551,000 , region1 = Brazil , pop1 = 25–33 million , ref1 = , region2 = Argentina , pop2 = 20–25 million , ref2 = , region3 = United States , pop3 = 17-20 million , ref3 = , region4 = France , pop4 = 1-5 million , ref4 = , region5 = Venezuela , pop5 = 1-5 million , ref5 = , region6 = Paraguay , pop6 = 2.5 million , region7 = Colombia , pop7 = 2 million , ref7 = , region8 = Canada , pop8 = 1.5 million , ref8 = , region9 = Australia , pop9 = 1.0 million , ref9 = , region10 = Uruguay , pop10 = 1.0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
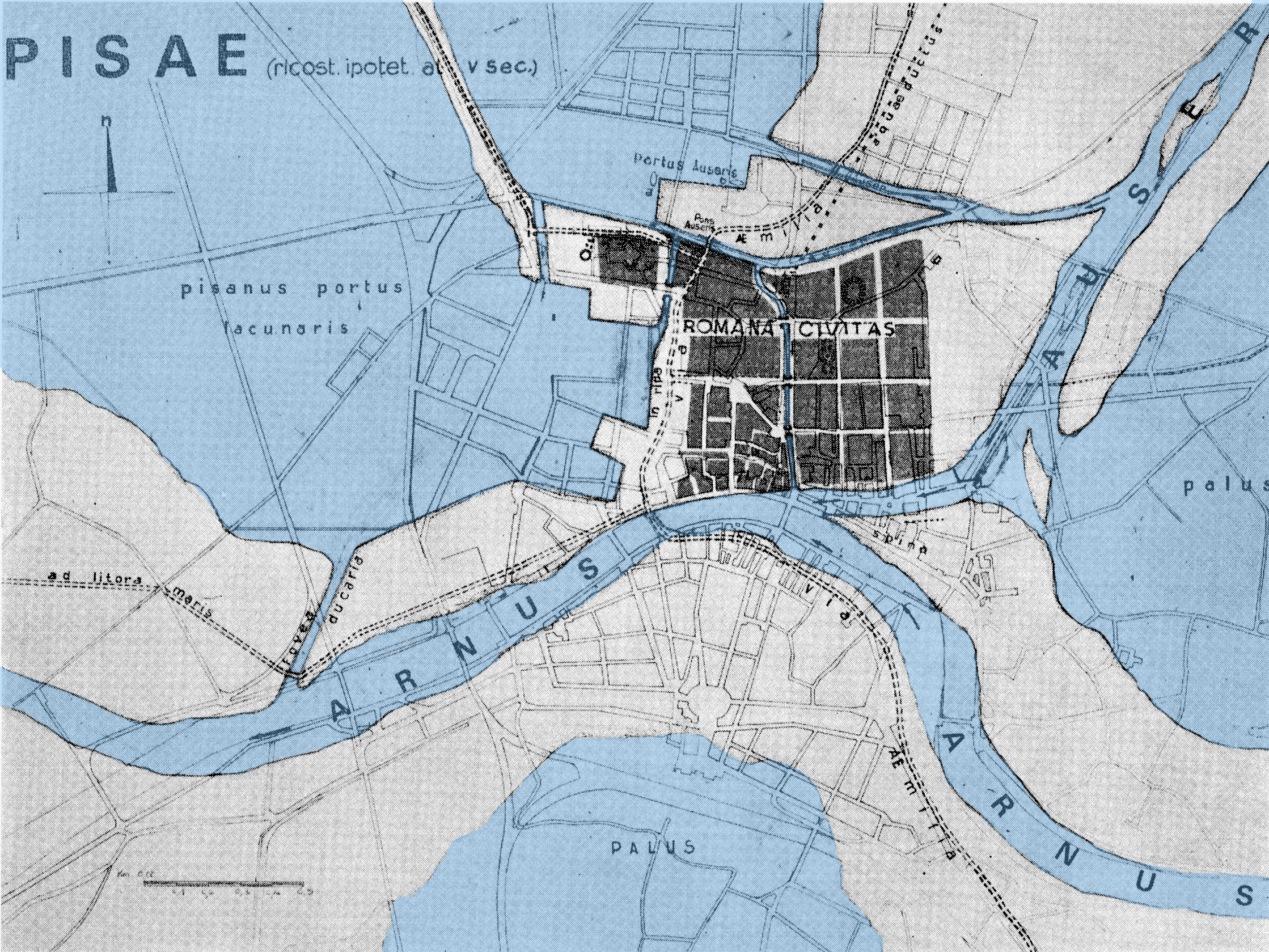
Pisa
Pisa ( , or ) is a city and ''comune'' in Tuscany, central Italy, straddling the Arno just before it empties into the Ligurian Sea. It is the capital city of the Province of Pisa. Although Pisa is known worldwide for its leaning tower, the city contains more than twenty other historic churches, several medieval palaces, and bridges across the Arno. Much of the city's architecture was financed from its history as one of the Italian maritime republics. The city is also home to the University of Pisa, which has a history going back to the 12th century, the Scuola Normale Superiore di Pisa, founded by Napoleon in 1810, and its offshoot, the Sant'Anna School of Advanced Studies.Scuola Superiore Sant'Anna di Pisa Information statistics History
|
Keith Devlin
Keith J. Devlin (born 16 March 1947) is a British mathematician and popular science writer. Since 1987 he has lived in the United States. He has dual British-American citizenship.Curriculum vitae Profkeithdevlin.com, accessed 3 February 2014. Biography He was born and grew up in England, in . There he attended a local primary school followed by Greatfield High School in . In the last school year he was appointed head boy. ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |