Spherical Product on:
[Wikipedia]
[Google]
[Amazon]
A sphere (from
 As mentioned earlier is the sphere's radius; any line from the center to a point on the sphere is also called a radius. 'Radius' is used in two senses: as a line segment and also as its length.
If a radius is extended through the center to the opposite side of the sphere, it creates a
As mentioned earlier is the sphere's radius; any line from the center to a point on the sphere is also called a radius. 'Radius' is used in two senses: as a line segment and also as its length.
If a radius is extended through the center to the opposite side of the sphere, it creates a
 In three dimensions, the
In three dimensions, the
 In their book ''Geometry and the Imagination'',
In their book ''Geometry and the Imagination'',
 The basic elements of
The basic elements of


 In
In
 Another kind of spherical spiral is the Clelia curve, for which the
Another kind of spherical spiral is the Clelia curve, for which the
 If a sphere is intersected by another surface, there may be more complicated spherical curves.
;Example: sphere–cylinder
The intersection of the sphere with equation and the cylinder with equation is not just one or two circles. It is the solution of the non-linear system of equations
:
:
(see
If a sphere is intersected by another surface, there may be more complicated spherical curves.
;Example: sphere–cylinder
The intersection of the sphere with equation and the cylinder with equation is not just one or two circles. It is the solution of the non-linear system of equations
:
:
(see
File:Einstein gyro gravity probe b.jpg, An image of one of the most accurate human-made spheres, as it refracts the image of New Scientist , Technology , Roundest objects in the world created
File:King of spades- spheres.jpg, Deck of playing cards illustrating engineering instruments, England, 1702.
Surface area of sphere proof
{{Authority control Differential geometry Differential topology Elementary geometry Elementary shapes Homogeneous spaces Surfaces Topology
Greek
Greek may refer to:
Anything of, from, or related to Greece, a country in Southern Europe:
*Greeks, an ethnic group
*Greek language, a branch of the Indo-European language family
**Proto-Greek language, the assumed last common ancestor of all kno ...
, ) is a surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
analogous to the circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
, a curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
. In solid geometry
Solid geometry or stereometry is the geometry of Three-dimensional space, three-dimensional Euclidean space (3D space).
A solid figure is the region (mathematics), region of 3D space bounded by a two-dimensional closed surface; for example, a ...
, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three- ...
.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is th ...
''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.
The sphere is a fundamental surface in many fields of mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble
Bubble, Bubbles or The Bubble may refer to:
Common uses
* Bubble (physics), a globule of one substance in another, usually gas in a liquid
** Soap bubble
* Economic bubble, a situation where asset prices are much higher than underlying fundame ...
s such as soap bubble
A soap bubble (commonly referred to as simply a bubble) is an extremely thin soap film, film of soap or detergent and water enclosing air that forms a hollow sphere with an iridescent surface. Soap bubbles usually last for only a few seconds b ...
s take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography
Geography (from Ancient Greek ; combining 'Earth' and 'write', literally 'Earth writing') is the study of the lands, features, inhabitants, and phenomena of Earth. Geography is an all-encompassing discipline that seeks an understanding o ...
, and the celestial sphere
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, ...
is an important concept in astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
. Manufactured items including pressure vessels
A pressure vessel is a container designed to hold gases or liquids at a pressure substantially different from the ambient pressure.
Construction methods and materials may be chosen to suit the pressure application, and will depend on the size o ...
and most curved mirror
A curved mirror is a mirror with a curved reflecting surface. The surface may be either ''convex'' (bulging outward) or ''concave'' (recessed inward). Most curved mirrors have surfaces that are shaped like part of a sphere, but other shapes are ...
s and lens
A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements'') ...
es are based on spheres. Spheres roll smoothly in any direction, so most ball
A ball is a round object (usually spherical, but sometimes ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for s ...
s used in sports and toys are spherical, as are ball bearings
A ball bearing is a type of rolling-element bearing that uses balls to maintain the separation between the bearing races.
The purpose of a ball bearing is to reduce rotational friction and support radial and axial loads. It achieves this ...
.
Basic terminology
 As mentioned earlier is the sphere's radius; any line from the center to a point on the sphere is also called a radius. 'Radius' is used in two senses: as a line segment and also as its length.
If a radius is extended through the center to the opposite side of the sphere, it creates a
As mentioned earlier is the sphere's radius; any line from the center to a point on the sphere is also called a radius. 'Radius' is used in two senses: as a line segment and also as its length.
If a radius is extended through the center to the opposite side of the sphere, it creates a diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions a ...
. Like the radius, the length of a diameter is also called the diameter, and denoted . Diameters are the longest line segments that can be drawn between two points on the sphere: their length is twice the radius, . Two points on the sphere connected by a diameter are antipodal point
In mathematics, two points of a sphere (or n-sphere, including a circle) are called antipodal or diametrically opposite if they are the endpoints of a diameter, a straight line segment between two points on a sphere and passing through its cen ...
s of each other.
A unit sphere
In mathematics, a unit sphere is a sphere of unit radius: the locus (mathematics), set of points at Euclidean distance 1 from some center (geometry), center point in three-dimensional space. More generally, the ''unit -sphere'' is an n-sphere, -s ...
is a sphere with unit radius (). For convenience, spheres are often taken to have their center at the origin of the coordinate system
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the position of the points or other geometric elements on a manifold such as Euclidean space. The coordinates are ...
, and spheres in this article have their center at the origin unless a center is mentioned.
A ''great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Discussion
Any arc of a great circle is a geodesic of the sphere, so that great circles in spher ...
'' on the sphere has the same center and radius as the sphere, and divides it into two equal ''hemispheres''.
Although the figure of Earth
In geodesy, the figure of the Earth is the size and shape used to model planet Earth. The kind of figure depends on application, including the precision needed for the model. A spherical Earth is a well-known historical approximation that is s ...
is not perfectly spherical, terms borrowed from geography are convenient to apply to the sphere.
A particular line passing through its center defines an ''axis
An axis (: axes) may refer to:
Mathematics
*A specific line (often a directed line) that plays an important role in some contexts. In particular:
** Coordinate axis of a coordinate system
*** ''x''-axis, ''y''-axis, ''z''-axis, common names ...
'' (as in Earth's axis of rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
).
The sphere-axis intersection defines two antipodal ''poles'' (''north pole'' and ''south pole''). The great circle equidistant to the poles is called the ''equator
The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumferen ...
''. Great circles through the poles are called lines of longitude
Longitude (, ) is a geographic coordinate that specifies the east- west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek lett ...
or ''meridians''. Small circles on the sphere that are parallel to the equator are circles of latitude (or ''parallels''). In geometry unrelated to astronomical bodies, geocentric terminology should be used only for illustration and noted as such, unless there is no chance of misunderstanding.
Mathematicians consider a sphere to be a two-dimensional
A two-dimensional space is a mathematical space with two dimensions, meaning points have two degrees of freedom: their locations can be locally described with two coordinates or they can move in two independent directions. Common two-dimension ...
closed surface
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces ari ...
embedded in three-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. They draw a distinction between a ''sphere'' and a ''ball
A ball is a round object (usually spherical, but sometimes ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for s ...
'', which is a solid figure
Solid geometry or stereometry is the geometry of three-dimensional Euclidean space (3D space).
A solid figure is the region of 3D space bounded by a two-dimensional closed surface; for example, a solid ball consists of a sphere and its inte ...
, a three-dimensional manifold with boundary
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a n ...
that includes the volume contained by the sphere. An ''open ball'' excludes the sphere itself, while a ''closed ball'' includes the sphere: a closed ball is the union of the open ball and the sphere, and a sphere is the boundary of a (closed or open) ball. The distinction between ''ball'' and ''sphere'' has not always been maintained and especially older mathematical references talk about a sphere as a solid. The distinction between "circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
" and " disk" in the plane is similar.
Small spheres or balls are sometimes called ''spherules'' (e.g., in Martian spherules
Martian spherules (also known as hematite spherules, blueberries, & Martian blueberries) are small spherules (roughly spherical pebbles) that are rich in an iron oxide (grey hematite, α-Fe2O3) and are found at Meridiani Planum (a large plain on M ...
).
Equations
Inanalytic geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineering, and als ...
, a sphere with center and radius is the locus of all points such that
:
Since it can be expressed as a quadratic polynomial, a sphere is a quadric surface
In mathematics, a quadric or quadric surface is a generalization of conic sections (ellipses, parabolas, and hyperbolas). In three-dimensional space, quadrics include ellipsoids, paraboloids, and hyperboloids.
More generally, a quadric hyper ...
, a type of algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two (as a complex manifold, when it is non-singular) and so of di ...
.
Let be real numbers with and put
:
Then the equation
:
has no real points as solutions if and is called the equation of an imaginary sphere. If , the only solution of is the point and the equation is said to be the equation of a point sphere. Finally, in the case , is an equation of a sphere whose center is and whose radius is .
If in the above equation is zero then is the equation of a plane. Thus, a plane may be thought of as a sphere of infinite radius whose center is a point at infinity
In geometry, a point at infinity or ideal point is an idealized limiting point at the "end" of each line.
In the case of an affine plane (including the Euclidean plane), there is one ideal point for each pencil of parallel lines of the plane. Ad ...
..
Parametric
Aparametric equation
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point (mathematics), point, as Function (mathematics), functions of one or several variable (mathematics), variables called parameters.
In the case ...
for the sphere with radius and center can be parameterized using trigonometric function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
s.
:
The symbols used here are the same as those used in spherical coordinates
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
. is constant, while varies from 0 to and varies from 0 to 2.
Properties
Enclosed volume
volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
inside a sphere (that is, the volume of a ball
A ball is a round object (usually spherical, but sometimes ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for s ...
, but classically referred to as the volume of a sphere) is
:
where is the radius and is the diameter of the sphere. Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
first derived this formula (''On the Sphere and Cylinder
''On the Sphere and Cylinder'' () is a treatise that was published by Archimedes in two volumes . It most notably details how to find the surface area of a sphere and the volume of the contained ball and the analogous values for a cylinder, and w ...
'' c. 225 BCE) by showing that the volume inside a sphere is twice the volume between the sphere and the circumscribe In geometry, a circumscribed circle for a set of points is a circle passing through each of them. Such a circle is said to ''circumscribe'' the points or a polygon formed from them; such a polygon is said to be ''inscribed'' in the circle.
* Circum ...
d cylinder
A cylinder () has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an infinite ...
of that sphere (having the height and diameter equal to the diameter of the sphere). This may be proved by inscribing a cone upside down into semi-sphere, noting that the area of a cross section of the cone plus the area of a cross section of the sphere is the same as the area of the cross section of the circumscribing cylinder, and applying Cavalieri's principle
In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows:
* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that pl ...
. This formula can also be derived using integral calculus
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Int ...
(i.e., disk integration) to sum the volumes of an infinite number
In mathematics, transfinite numbers or infinite numbers are numbers that are " infinite" in the sense that they are larger than all finite numbers. These include the transfinite cardinals, which are cardinal numbers used to quantify the size of inf ...
of circular disks of infinitesimally small thickness stacked side by side and centered along the -axis from to , assuming the sphere of radius is centered at the origin.
At any given , the incremental volume () equals the product of the cross-sectional area of the disk at and its thickness ():
:
The total volume is the summation of all incremental volumes:
:
In the limit as approaches zero, this equation becomes:
:
At any given , a right-angled triangle connects , and to the origin; hence, applying the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
yields:
:
Using this substitution gives
:
which can be evaluated to give the result
:
An alternative formula is found using spherical coordinates
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
, with volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates. Thus a volume element is an expression of the form
\ma ...
:
so
:
For most practical purposes, the volume inside a sphere inscribed
An inscribed triangle of a circle
In geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figure F is inscribed in figure G" means precisely the same th ...
in a cube can be approximated as 52.4% of the volume of the cube, since , where is the diameter of the sphere and also the length of a side of the cube and ≈ 0.5236. For example, a sphere with diameter 1 m has 52.4% the volume of a cube with edge length 1m, or about 0.524 m3.
Surface area
Thesurface area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the d ...
of a sphere of radius is:
:
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
first derived this formula from the fact that the projection to the lateral surface of a circumscribe In geometry, a circumscribed circle for a set of points is a circle passing through each of them. Such a circle is said to ''circumscribe'' the points or a polygon formed from them; such a polygon is said to be ''inscribed'' in the circle.
* Circum ...
d cylinder is area-preserving. Another approach to obtaining the formula comes from the fact that it equals the derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
of the formula for the volume with respect to because the total volume inside a sphere of radius can be thought of as the summation of the surface area of an infinite number of spherical shells of infinitesimal thickness concentrically stacked inside one another from radius 0 to radius . At infinitesimal thickness the discrepancy between the inner and outer surface area of any given shell is infinitesimal, and the elemental volume at radius is simply the product of the surface area at radius and the infinitesimal thickness.
At any given radius , the incremental volume () equals the product of the surface area at radius () and the thickness of a shell ():
:
The total volume is the summation of all shell volumes:
:
In the limit as approaches zero this equation becomes:
:
Substitute :
:
Differentiating both sides of this equation with respect to yields as a function of :
:
This is generally abbreviated as:
:
where is now considered to be the fixed radius of the sphere.
Alternatively, the area element on the sphere is given in spherical coordinates
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
by . The total area can thus be obtained by integration:
:
The sphere has the smallest surface area of all surfaces that enclose a given volume, and it encloses the largest volume among all closed surfaces with a given surface area. The sphere therefore appears in nature: for example, bubbles and small water drops are roughly spherical because the surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Ge ...
locally minimizes surface area.
The surface area relative to the mass of a ball is called the specific surface area
Specific surface area (SSA) is a property of solids defined as the total surface area (SA) of a material per unit mass, (with units of m2/kg or m2/g). Alternatively, it may be defined as SA per solid or bulk volume (units of m2/m3 or m−1).
I ...
and can be expressed from the above stated equations as
:
where is the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
(the ratio of mass to volume).
Other geometric properties
A sphere can be constructed as the surface formed by rotating acircle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
one half revolution about any of its diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions a ...
s; this is very similar to the traditional definition of a sphere as given in Euclid's Elements
The ''Elements'' ( ) is a mathematics, mathematical treatise written 300 BC by the Ancient Greek mathematics, Ancient Greek mathematician Euclid.
''Elements'' is the oldest extant large-scale deductive treatment of mathematics. Drawing on the w ...
. Since a circle is a special type of ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
, a sphere is a special type of ellipsoid of revolution
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circu ...
. Replacing the circle with an ellipse rotated about its major axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longe ...
, the shape becomes a prolate spheroid
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface (mathematics), surface obtained by Surface of revolution, rotating an ellipse about one of its principal axes; in other words, an ellipsoid with t ...
; rotated about the minor axis, an oblate spheroid.
A sphere is uniquely determined by four points that are not coplanar
In geometry, a set of points in space are coplanar if there exists a geometric plane that contains them all. For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. How ...
. More generally, a sphere is uniquely determined by four conditions such as passing through a point, being tangent to a plane, etc. This property is analogous to the property that three non-collinear points determine a unique circle in a plane.
Consequently, a sphere is uniquely determined by (that is, passes through) a circle and a point not in the plane of that circle.
By examining the common solutions of the equations of two spheres, it can be seen that two spheres intersect in a circle and the plane containing that circle is called the radical plane of the intersecting spheres. Although the radical plane is a real plane, the circle may be imaginary (the spheres have no real point in common) or consist of a single point (the spheres are tangent at that point)..
The angle between two spheres at a real point of intersection is the dihedral angle determined by the tangent planes to the spheres at that point. Two spheres intersect at the same angle at all points of their circle of intersection. They intersect at right angles (are orthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...
) if and only if the square of the distance between their centers is equal to the sum of the squares of their radii.
Pencil of spheres
If and are the equations of two distinct spheres then : is also the equation of a sphere for arbitrary values of the parameters and . The set of all spheres satisfying this equation is called a pencil of spheres determined by the original two spheres. In this definition a sphere is allowed to be a plane (infinite radius, center at infinity) and if both the original spheres are planes then all the spheres of the pencil are planes, otherwise there is only one plane (the radical plane) in the pencil.Properties of the sphere
 In their book ''Geometry and the Imagination'',
In their book ''Geometry and the Imagination'', David Hilbert
David Hilbert (; ; 23 January 1862 – 14 February 1943) was a German mathematician and philosopher of mathematics and one of the most influential mathematicians of his time.
Hilbert discovered and developed a broad range of fundamental idea ...
and Stephan Cohn-Vossen describe eleven properties of the sphere and discuss whether these properties uniquely determine the sphere. Several properties hold for the plane, which can be thought of as a sphere with infinite radius. These properties are:
#''The points on the sphere are all the same distance from a fixed point. Also, the ratio of the distance of its points from two fixed points is constant.''
#: The first part is the usual definition of the sphere and determines it uniquely. The second part can be easily deduced and follows a similar result
A result (also called upshot) is the outcome or consequence of a sequence of actions or events. Possible results include gain, injury, value, and victory. Some types of results include the outcome of an action, the final value of a calculation ...
of Apollonius of Perga
Apollonius of Perga ( ; ) was an ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the earlier contributions of Euclid and Archimedes on the topic, he brought them to the state prior to the invention o ...
for the circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
. This second part also holds for the plane.
#''The contours and plane sections of the sphere are circles.''
#: This property defines the sphere uniquely.
#''The sphere has constant width and constant girth.''
#: The width of a surface is the distance between pairs of parallel tangent planes. Numerous other closed convex surfaces have constant width, for example the Meissner body. The girth of a surface is the circumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length arou ...
of the boundary of its orthogonal projection on to a plane. Each of these properties implies the other.
#''All points of a sphere are umbilics.''
#: At any point on a surface a normal direction
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the cur ...
is at right angles to the surface because on the sphere these are the lines radiating out from the center of the sphere. The intersection of a plane that contains the normal with the surface will form a curve that is called a ''normal section,'' and the curvature of this curve is the ''normal curvature''. For most points on most surfaces, different sections will have different curvatures; the maximum and minimum values of these are called the principal curvature
In differential geometry, the two principal curvatures at a given point of a surface (mathematics), surface are the maximum and minimum values of the curvature as expressed by the eigenvalues of the shape operator at that point. They measure how ...
s. Any closed surface will have at least four points called ''umbilical point
In the differential geometry of surfaces in three dimensions, umbilics or umbilical points are points on a surface that are locally spherical. At such points the normal curvatures in all directions are equal, hence, both principal curvatures are e ...
s''. At an umbilic all the sectional curvatures are equal; in particular the principal curvature
In differential geometry, the two principal curvatures at a given point of a surface (mathematics), surface are the maximum and minimum values of the curvature as expressed by the eigenvalues of the shape operator at that point. They measure how ...
s are equal. Umbilical points can be thought of as the points where the surface is closely approximated by a sphere.
#: For the sphere the curvatures of all normal sections are equal, so every point is an umbilic. The sphere and plane are the only surfaces with this property.
#''The sphere does not have a surface of centers.''
#: For a given normal section exists a circle of curvature that equals the sectional curvature, is tangent to the surface, and the center lines of which lie along on the normal line. For example, the two centers corresponding to the maximum and minimum sectional curvatures are called the ''focal points'', and the set of all such centers forms the focal surface.
#: For most surfaces the focal surface forms two sheets that are each a surface and meet at umbilical points. Several cases are special:
#: * For channel surface
In geometry and topology, a channel or canal surface is a surface formed as the Envelope (mathematics), envelope of a family of spheres whose centers lie on a space curve, its ''Generatrix, directrix''. If the radii of the generating spheres ar ...
s one sheet forms a curve and the other sheet is a surface
#: * For cones
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the ''apex'' or '' vertex''.
A cone is formed by a set of line segments, half-lines, ...
, cylinders, tori and cyclides both sheets form curves.
#: * For the sphere the center of every osculating circle is at the center of the sphere and the focal surface forms a single point. This property is unique to the sphere.
#''All geodesics of the sphere are closed curves.''
#: Geodesics
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connec ...
are curves on a surface that give the shortest distance between two points. They are a generalization of the concept of a straight line in the plane. For the sphere the geodesics are great circles. Many other surfaces share this property.
#''Of all the solids having a given volume, the sphere is the one with the smallest surface area; of all solids having a given surface area, the sphere is the one having the greatest volume.''
#: It follows from isoperimetric inequality
In mathematics, the isoperimetric inequality is a geometric inequality involving the square of the circumference of a closed curve in the plane and the area of a plane region it encloses, as well as its various generalizations. '' Isoperimetric'' ...
. These properties define the sphere uniquely and can be seen in soap bubble
A soap bubble (commonly referred to as simply a bubble) is an extremely thin soap film, film of soap or detergent and water enclosing air that forms a hollow sphere with an iridescent surface. Soap bubbles usually last for only a few seconds b ...
s: a soap bubble will enclose a fixed volume, and surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Ge ...
minimizes its surface area for that volume. A freely floating soap bubble therefore approximates a sphere (though such external forces as gravity will slightly distort the bubble's shape). It can also be seen in planets and stars where gravity minimizes surface area for large celestial bodies.
#''The sphere has the smallest total mean curvature among all convex solids with a given surface area.''
#: The mean curvature
In mathematics, the mean curvature H of a surface S is an ''extrinsic'' measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space.
The ...
is the average of the two principal curvatures, which is constant because the two principal curvatures are constant at all points of the sphere.
#''The sphere has constant mean curvature.''
#: The sphere is the only embedded surface that lacks boundary or singularities with constant positive mean curvature. Other such immersed surfaces as minimal surface
In mathematics, a minimal surface is a surface that locally minimizes its area. This is equivalent to having zero mean curvature (see definitions below).
The term "minimal surface" is used because these surfaces originally arose as surfaces that ...
s have constant mean curvature.
#''The sphere has constant positive Gaussian curvature.''
#: Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a smooth Surface (topology), surface in three-dimensional space at a point is the product of the principal curvatures, and , at the given point:
K = \kappa_1 \kappa_2.
For ...
is the product of the two principal curvatures. It is an intrinsic property that can be determined by measuring length and angles and is independent of how the surface is embedded in space. Hence, bending a surface will not alter the Gaussian curvature, and other surfaces with constant positive Gaussian curvature can be obtained by cutting a small slit in the sphere and bending it. All these other surfaces would have boundaries, and the sphere is the only surface that lacks a boundary with constant, positive Gaussian curvature. The pseudosphere
In geometry, a pseudosphere is a surface with constant negative Gaussian curvature.
A pseudosphere of radius is a surface in \mathbb^3 having Gaussian curvature, curvature −1/''R''2 at each point. Its name comes from the analogy with the sphere ...
is an example of a surface with constant negative Gaussian curvature.
#''The sphere is transformed into itself by a three-parameter family of rigid motions.''
#: Rotating around any axis a unit sphere at the origin will map the sphere onto itself. Any rotation about a line through the origin can be expressed as a combination of rotations around the three-coordinate axis (see Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the Orientation (geometry), orientation of a rigid body with respect to a fixed coordinate system.Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189� ...
). Therefore, a three-parameter family of rotations exists such that each rotation transforms the sphere onto itself; this family is the rotation group SO(3)
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space \R^3 under the operation of composition.
By definition, a rotation about the origin is a ...
. The plane is the only other surface with a three-parameter family of transformations (translations along the - and -axes and rotations around the origin). Circular cylinders are the only surfaces with two-parameter families of rigid motions and the surfaces of revolution and helicoid
The helicoid, also known as helical surface, is a smooth Surface (differential geometry), surface embedded in three-dimensional space. It is the surface traced by an infinite line that is simultaneously being rotated and lifted along its Rotation ...
s are the only surfaces with a one-parameter family.
Treatment by area of mathematics
Spherical geometry
 The basic elements of
The basic elements of Euclidean plane geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, '' Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (pos ...
are points
A point is a small dot or the sharp tip of something. Point or points may refer to:
Mathematics
* Point (geometry), an entity that has a location in space or on a plane, but has no extent; more generally, an element of some abstract topologica ...
and lines. On the sphere, points are defined in the usual sense. The analogue of the "line" is the geodesic
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a conn ...
, which is a great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Discussion
Any arc of a great circle is a geodesic of the sphere, so that great circles in spher ...
; the defining characteristic of a great circle is that the plane containing all its points also passes through the center of the sphere. Measuring by arc length
Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the ...
shows that the shortest path between two points lying on the sphere is the shorter segment of the great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Discussion
Any arc of a great circle is a geodesic of the sphere, so that great circles in spher ...
that includes the points.
Many theorems from classical geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, '' Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (pos ...
hold true for spherical geometry as well, but not all do because the sphere fails to satisfy some of classical geometry's postulate
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or f ...
s, including the parallel postulate
In geometry, the parallel postulate is the fifth postulate in Euclid's ''Elements'' and a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
If a line segment intersects two straight lines forming two interior ...
. In spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the edge (geometry), sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, ge ...
, angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s are defined between great circles. Spherical trigonometry differs from ordinary trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The fiel ...
in many respects. For example, the sum of the interior angles of a spherical triangle
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are gre ...
always exceeds 180 degrees. Also, any two similar spherical triangles are congruent.
Any pair of points on a sphere that lie on a straight line through the sphere's center (i.e., the diameter) are called ''antipodal points''on the sphere, the distance between them is exactly half the length of the circumference. Any other (i.e., not antipodal) pair of distinct points on a sphere
*lie on a unique great circle,
*segment it into one minor (i.e., shorter) and one major (i.e., longer) arc, and
*have the minor arc's length be the ''shortest distance'' between them on the sphere.
Spherical geometry is a form of elliptic geometry
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines ...
, which together with hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or János Bolyai, Bolyai–Nikolai Lobachevsky, Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For a ...
makes up non-Euclidean geometry
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean ge ...
.
Differential geometry
The sphere is asmooth surface
In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth manifold, smooth Surface (topology), surfaces with various additional structures, most often, a Riemannian metric.
Surfaces have been extensiv ...
with constant Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a smooth Surface (topology), surface in three-dimensional space at a point is the product of the principal curvatures, and , at the given point:
K = \kappa_1 \kappa_2.
For ...
at each point equal to . As per Gauss's Theorema Egregium, this curvature is independent of the sphere's embedding in 3-dimensional space. Also following from Gauss, a sphere cannot be mapped to a plane while maintaining both areas and angles. Therefore, any map projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, ...
introduces some form of distortion.
A sphere of radius has area element . This can be found from the volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates. Thus a volume element is an expression of the form
\ma ...
in spherical coordinates
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
with held constant.
A sphere of any radius centered at zero is an integral surface
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations.
Name
Integral curves are known by various other names, depending on the nature and interpret ...
of the following differential form
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications ...
:
:
This equation reflects that the position vector and tangent plane
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o ...
at a point are always orthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...
to each other. Furthermore, the outward-facing normal vector
In geometry, a normal is an object (e.g. a line, ray, or vector) that is perpendicular to a given object. For example, the normal line to a plane curve at a given point is the infinite straight line perpendicular to the tangent line to the cu ...
is equal to the position vector scaled by .
In Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as manifold, smooth manifolds with a ''Riemannian metric'' (an inner product on the tangent space at each point that varies smooth function, smo ...
, the filling area conjecture In differential geometry, Mikhail Gromov's filling area conjecture asserts that the hemisphere has minimum area among the orientable surfaces that fill a closed curve of given length without introducing shortcuts between its points.
Definitions ...
states that the hemisphere is the optimal (least area) isometric filling of the Riemannian circle
In mathematics, a metric circle is the metric space of arc length on a circle, or equivalently on any rectifiable simple closed curve of bounded length. The metric spaces that can be embedded into metric circles can be characterized by a four-p ...
.
Topology
Remarkably, it is possible to turn an ordinary sphere inside out in athree-dimensional space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three- ...
with possible self-intersections but without creating any creases, in a process called sphere eversion
In differential topology, sphere eversion is a theoretical process of turning a sphere inside out in a three-dimensional space (the word ''wikt:eversion#English, eversion'' means "turning inside out"). It is possible to smoothly and continuou ...
.
The antipodal quotient of the sphere is the surface called the real projective plane
In mathematics, the real projective plane, denoted or , is a two-dimensional projective space, similar to the familiar Euclidean plane in many respects but without the concepts of distance, circles, angle measure, or parallelism. It is the sett ...
, which can also be thought of as the Northern Hemisphere
The Northern Hemisphere is the half of Earth that is north of the equator. For other planets in the Solar System, north is defined by humans as being in the same celestial sphere, celestial hemisphere relative to the invariable plane of the Solar ...
with antipodal points of the equator identified.
Curves on a sphere
Circles
Circles on the sphere are, like circles in the plane, made up of all points a certain distance from a fixed point on the sphere. The intersection of a sphere and a plane is a circle, a point, or empty. Great circles are the intersection of the sphere with a plane passing through the center of a sphere: others are called small circles. More complicated surfaces may intersect a sphere in circles, too: the intersection of a sphere with asurface of revolution
A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersec ...
whose axis contains the center of the sphere (are ''coaxial'') consists of circles and/or points if not empty. For example, the diagram to the right shows the intersection of a sphere and a cylinder, which consists of two circles. If the cylinder radius were that of the sphere, the intersection would be a single circle. If the cylinder radius were larger than that of the sphere, the intersection would be empty.
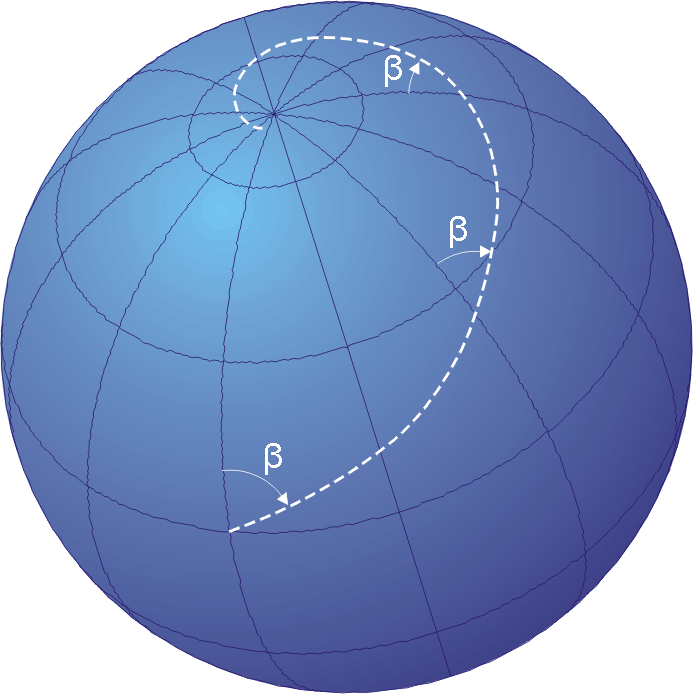
Loxodrome
 In
In navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navig ...
, a ''loxodrome'' or ''rhumb line'' is a path whose bearing, the angle between its tangent and due North, is constant. Loxodromes project to straight lines under the Mercator projection. Two special cases are the meridians which are aligned directly North–South and parallels which are aligned directly East–West. For any other bearing, a loxodrome spirals infinitely around each pole. For the Earth modeled as a sphere, or for a general sphere given a spherical coordinate system
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
, such a loxodrome is a kind of spherical spiral
In mathematics, a spiral is a curve which emanates from a point, moving further away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.
Two-dimensional
A two-dimension ...
.
Clelia curves
longitude
Longitude (, ) is a geographic coordinate that specifies the east- west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek lett ...
(or azimuth) and the colatitude
In a spherical coordinate system, a colatitude is the complementary angle of a given latitude, i.e. the difference between a right angle and the latitude. In geography, Southern latitudes are defined to be negative, and as a result the colatitude ...
(or polar angle) are in a linear relationship, . Clelia curves project to straight lines under the equirectangular projection
The equirectangular projection (also called the equidistant cylindrical projection or la carte parallélogrammatique projection), and which includes the special case of the plate carrée projection (also called the geographic projection, lat/l ...
. Viviani's curve
In mathematics, Viviani's curve, also known as Viviani's window, is a Lemniscate, figure-eight-shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder (geometry), cylinder that ...
() is a special case. Clelia curves approximate the ground track
A satellite ground track or satellite ground trace is the path on the surface of a planet directly below a satellite's trajectory. It is also known as a suborbital track or subsatellite track, and is the vertical projection of the satellite's ...
of satellites in polar orbit
A polar orbit is one in which a satellite passes above or nearly above both poles of the body being orbited (usually a planet such as the Earth, but possibly another body such as the Moon or Sun) on each revolution. It has an inclination of abo ...
.
Spherical conics
The analog of aconic section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, tho ...
on the sphere is a spherical conic
In mathematics, a spherical conic or sphero-conic is a curve on the sphere, the intersection of the sphere with a concentric elliptic cone. It is the spherical analog of a conic section (ellipse, parabola, or hyperbola) in the plane, and as in ...
, a quartic curve which can be defined in several equivalent ways.
*The intersection of a sphere with a quadratic cone whose vertex is the sphere center
*The intersection of a sphere with an elliptic or hyperbolic cylinder whose axis passes through the sphere center
*The locus of points whose sum or difference of great-circle distance
The great-circle distance, orthodromic distance, or spherical distance is the distance between two points on a sphere, measured along the great-circle arc between them. This arc is the shortest path between the two points on the surface of the ...
s from a pair of foci
Focus (: foci or focuses) may refer to:
Arts
* Focus or Focus Festival, former name of the Adelaide Fringe arts festival in East Australia Film
* ''Focus'' (2001 film), a 2001 film based on the Arthur Miller novel
* ''Focus'' (2015 film), a 201 ...
is a constant
Many theorems relating to planar conic sections also extend to spherical conics.
Intersection of a sphere with a more general surface
implicit curve
In mathematics, an implicit curve is a plane curve defined by an implicit equation relating two coordinate variables, commonly ''x'' and ''y''. For example, the unit circle is defined by the implicit equation x^2+y^2=1. In general, every implic ...
and the diagram)
Generalizations
Ellipsoids
Anellipsoid
An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional Scaling (geometry), scalings, or more generally, of an affine transformation.
An ellipsoid is a quadric surface; that is, a Surface (mathemat ...
is a sphere that has been stretched or compressed in one or more directions. More exactly, it is the image of a sphere under an affine transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, '' affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
More general ...
. An ellipsoid bears the same relationship to the sphere that an ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
does to a circle.
Dimensionality
Spheres can be generalized to spaces of any number ofdimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coo ...
s. For any natural number
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive in ...
, an ''-sphere,'' often denoted , is the set of points in ()-dimensional Euclidean space that are at a fixed distance from a central point of that space, where is, as before, a positive real number. In particular:
*: a 0-sphere consists of two discrete points, and
*: a 1-sphere is a circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
of radius ''r''
*: a 2-sphere is an ordinary sphere
*: a 3-sphere
In mathematics, a hypersphere or 3-sphere is a 4-dimensional analogue of a sphere, and is the 3-dimensional n-sphere, ''n''-sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. The interior o ...
is a sphere in 4-dimensional Euclidean space.
Spheres for are sometimes called hypersphere
In mathematics, an -sphere or hypersphere is an - dimensional generalization of the -dimensional circle and -dimensional sphere to any non-negative integer .
The circle is considered 1-dimensional and the sphere 2-dimensional because a point ...
s.
The -sphere of unit radius centered at the origin is denoted and is often referred to as "the" -sphere. The ordinary sphere is a 2-sphere, because it is a 2-dimensional surface which is embedded in 3-dimensional space.
In topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, the -sphere is an example of a compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:
* Interstate compact, a type of agreement used by U.S. states
* Blood compact, an ancient ritual of the Philippines
* Compact government, a t ...
topological manifold
In topology, a topological manifold is a topological space that locally resembles real ''n''- dimensional Euclidean space. Topological manifolds are an important class of topological spaces, with applications throughout mathematics. All manifolds ...
without boundary. A topological sphere need not be smooth; if it is smooth, it need not be diffeomorphic
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.
Defini ...
to the Euclidean sphere (an exotic sphere
In an area of mathematics called differential topology, an exotic sphere is a differentiable manifold ''M'' that is homeomorphic but not diffeomorphic to the standard Euclidean ''n''-sphere. That is, ''M'' is a sphere from the point of view of ...
).
The sphere is the inverse image of a one-point set under the continuous function , so it is closed; is also bounded, so it is compact by the Heine–Borel theorem
In real analysis, the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:
For a subset S of Euclidean space \mathbb^n, the following two statements are equivalent:
*S is compact, that is, every open cover of S has a finite s ...
.
Metric spaces
More generally, in ametric space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), functi ...
, the sphere of center and radius is the set of points such that .
If the center is a distinguished point that is considered to be the origin of , as in a normed space, it is not mentioned in the definition and notation. The same applies for the radius if it is taken to equal one, as in the case of a unit sphere
In mathematics, a unit sphere is a sphere of unit radius: the locus (mathematics), set of points at Euclidean distance 1 from some center (geometry), center point in three-dimensional space. More generally, the ''unit -sphere'' is an n-sphere, -s ...
.
Unlike a ball
A ball is a round object (usually spherical, but sometimes ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for s ...
, even a large sphere may be an empty set. For example, in with Euclidean metric
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is oc ...
, a sphere of radius is nonempty only if can be written as sum of squares of integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
s.
An octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
is a sphere in taxicab geometry
Taxicab geometry or Manhattan geometry is geometry where the familiar Euclidean distance is ignored, and the distance between two points is instead defined to be the sum of the absolute differences of their respective Cartesian coordinates, a dis ...
, and a cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
is a sphere in geometry using the Chebyshev distance
In mathematics, Chebyshev distance (or Tchebychev distance), maximum metric, or L∞ metric is a metric defined on a real coordinate space where the distance between two points is the greatest of their differences along any coordinate dimensio ...
.
History
The geometry of the sphere was studied by the Greeks. ''Euclid's Elements
The ''Elements'' ( ) is a mathematics, mathematical treatise written 300 BC by the Ancient Greek mathematics, Ancient Greek mathematician Euclid.
''Elements'' is the oldest extant large-scale deductive treatment of mathematics. Drawing on the w ...
'' defines the sphere in book XI, discusses various properties of the sphere in book XII, and shows how to inscribe the five regular polyhedra within a sphere in book XIII. Euclid does not include the area and volume of a sphere, only a theorem that the volume of a sphere varies as the third power of its diameter, probably due to Eudoxus of Cnidus
Eudoxus of Cnidus (; , ''Eúdoxos ho Knídios''; ) was an Ancient Greece, ancient Greek Ancient Greek astronomy, astronomer, Greek mathematics, mathematician, doctor, and lawmaker. He was a student of Archytas and Plato. All of his original work ...
. The volume and area formulas were first determined in Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
's ''On the Sphere and Cylinder
''On the Sphere and Cylinder'' () is a treatise that was published by Archimedes in two volumes . It most notably details how to find the surface area of a sphere and the volume of the contained ball and the analogous values for a cylinder, and w ...
'' by the method of exhaustion
The method of exhaustion () is a method of finding the area of a shape by inscribing inside it a sequence of polygons (one at a time) whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the differ ...
. Zenodorus was the first to state that, for a given surface area, the sphere is the solid of maximum volume.
Archimedes wrote about the problem of dividing a sphere into segments whose volumes are in a given ratio, but did not solve it. A solution by means of the parabola and hyperbola was given by Dionysodorus. A similar problemto construct a segment equal in volume to a given segment, and in surface to another segmentwas solved later by al-Quhi.
Gallery
Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
in the background. This sphere was a fused quartz
Fused quartz, fused silica or quartz glass is a glass consisting of almost pure silica (silicon dioxide, SiO2) in amorphous (non-crystalline) form. This differs from all other commercial glasses, such as soda-lime glass, lead glass, or borosi ...
gyroscope
A gyroscope (from Ancient Greek γῦρος ''gŷros'', "round" and σκοπέω ''skopéō'', "to look") is a device used for measuring or maintaining Orientation (geometry), orientation and angular velocity. It is a spinning wheel or disc in ...
for the Gravity Probe B
Gravity Probe B (GP-B) was a satellite-based experiment whose objective was to test two previously-unverified predictions of general relativity: the geodetic effect and frame-dragging. This was to be accomplished by measuring, very precisely, t ...
experiment, and differs in shape from a perfect sphere by no more than 40 atoms (less than 10nm) of thickness. It was announced on 1 July 2008 that Australia
Australia, officially the Commonwealth of Australia, is a country comprising mainland Australia, the mainland of the Australia (continent), Australian continent, the island of Tasmania and list of islands of Australia, numerous smaller isl ...
n scientists had created even more nearly perfect spheres, accurate to 0.3nm, as part of an international hunt to find a new global standard kilogram.File:King of spades- spheres.jpg, Deck of playing cards illustrating engineering instruments, England, 1702.
King of spades
The king of spades is a playing card in the standard 52-card deck.
King of Spades may also refer to:
* ''King of Spades'' (novel), a 1966 novel by Frederick Manfred, the fourth book in ''The Buckskin Man Tales'' series
* King of Spades, a fictio ...
: Spheres
Regions
*Hemisphere *Spherical cap
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball (mathematics), ball cut off by a plane (mathematics), plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes thr ...
*Spherical lune
In spherical geometry, a spherical lune (or biangle) is an area on a sphere bounded by two half great circles which meet at antipodal points. It is an example of a digon, θ, with dihedral angle θ. The word "lune" derives from ''Luna (goddess ...
* Spherical polygon
*Spherical sector
In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed ...
*Spherical segment
In geometry, a spherical segment is the solid defined by cutting a sphere or a ball with a pair of parallel planes.
It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum.
The surface o ...
*Spherical wedge
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center' ...
*Spherical zone
In geometry, a spherical segment is the solid (geometry), solid defined by cutting a sphere or a ball (mathematics), ball with a pair of Parallel (geometry), parallel planes.
It can be thought of as a spherical cap with the top truncated, and ...
See also
*3-sphere
In mathematics, a hypersphere or 3-sphere is a 4-dimensional analogue of a sphere, and is the 3-dimensional n-sphere, ''n''-sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. The interior o ...
* Affine sphere
*Alexander horned sphere
The Alexander horned sphere is a pathological object in topology discovered by . It is a particular topological embedding of a two-dimensional sphere in three-dimensional space. Together with its inside, it is a topological 3-ball, the Alexande ...
*Celestial spheres
The celestial spheres, or celestial orbs, were the fundamental entities of the cosmological models developed by Plato, Eudoxus, Aristotle, Ptolemy, Copernicus, and others. In these celestial models, the apparent motions of the fixed star ...
*Curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
*Directional statistics
Directional statistics (also circular statistics or spherical statistics) is the subdiscipline of statistics that deals with directions (unit vectors in Euclidean space, R''n''), axes ( lines through the origin in R''n'') or rotations in R''n''. ...
*Dyson sphere
A Dyson sphere is a hypothetical megastructure that encompasses a star and captures a large percentage of its power output. The concept is a thought experiment that attempts to imagine how a spacefaring civilization would meet its energy re ...
* Gauss map
*Hand with Reflecting Sphere
''Hand with Reflecting Sphere'', also known as ''Self-Portrait in Spherical Mirror'', is a lithograph by Dutch artist M. C. Escher, first printed in January 1935. The piece depicts a hand holding a reflective sphere. In the reflection, most o ...
, M.C. Escher
Maurits Cornelis Escher (; ; 17 June 1898 – 27 March 1972) was a Dutch graphic artist who made woodcuts, lithography, lithographs, and mezzotints, many of which were Mathematics and art, inspired by mathematics.
Despite wide popular int ...
self-portrait drawing illustrating reflection and the optical properties of a mirror sphere
* Hoberman sphere
*Homology sphere
In algebraic topology, a homology sphere is an ''n''-manifold ''X'' having the homology groups of an ''n''-sphere, for some integer n\ge 1. That is,
:H_0(X,\Z) = H_n(X,\Z) = \Z
and
:H_i(X,\Z) = \ for all other ''i''.
Therefore ''X'' is a conne ...
*Homotopy groups of spheres
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure ...
*Homotopy sphere
In algebraic topology, a branch of mathematics, a homotopy sphere is an ''n''-manifold that is homotopy equivalent to the ''n''-sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a cu ...
*Lenart Sphere Lenart may refer to:
* Municipality of Lenart, Slovenia
* Lenart v Slovenskih Goricah, the seat of the Municipality of Lenart, Slovenia
* Lenart Regional Gifted Center, United States, school
* Lénárt sphere, an educational model for spherical ...
*Napkin ring problem
In geometry, the napkin-ring problem involves finding the volume of a "band" of specified height around a sphere, i.e. the part that remains after a hole in the shape of a circular cylinder is drilled through the center of the sphere. It is a co ...
* Orb (optics)
*Pseudosphere
In geometry, a pseudosphere is a surface with constant negative Gaussian curvature.
A pseudosphere of radius is a surface in \mathbb^3 having Gaussian curvature, curvature −1/''R''2 at each point. Its name comes from the analogy with the sphere ...
*Riemann sphere
In mathematics, the Riemann sphere, named after Bernhard Riemann,
is a Mathematical model, model of the extended complex plane (also called the closed complex plane): the complex plane plus one point at infinity. This extended plane represents ...
*Solid angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point.
The poin ...
*Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing p ...
*Spherical coordinates
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
*Spherical cow
file:SphericalCow2.gif, Comic of a spherical cow as illustrated by a 1996 meeting of the American Astronomical Association, in reference to astronomy modeling
The spherical cow is a humour, humorous metaphor for highly idealization (philosophy of ...
*Spherical helix, tangent indicatrix of a curve of constant precession
*Spherical polyhedron
In geometry, a spherical polyhedron or spherical tiling is a tessellation, tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called ''spherical polygons''. A polyhedron whose vertices are equi ...
*Sphericity
Sphericity is a measure of how closely the shape of a physical object resembles that of a perfect sphere. For example, the sphericity of the ball (bearing), balls inside a ball bearing determines the quality (business), quality of the bearing, ...
*Tennis ball theorem
In geometry, the tennis ball theorem states that any smooth curve on the surface of a sphere that divides the sphere into two equal-area subsets without touching or crossing itself must have at least four inflection points, points at which the cur ...
* Volume-equivalent radius
* Zoll sphere
Notes and references
Notes
References
Further reading
*. * *. *. *. *External links
* Mathematica/Uniform Spherical DistributionSurface area of sphere proof
{{Authority control Differential geometry Differential topology Elementary geometry Elementary shapes Homogeneous spaces Surfaces Topology