|
Solid Figure
In mathematics, solid geometry or stereometry is the traditional name for the geometry of three-dimensional, Euclidean spaces (i.e., 3D geometry). Stereometry deals with the measurements of volumes of various solid figures (or 3D figures), including pyramids, prisms and other polyhedrons; cylinders; cones; truncated cones; and balls bounded by spheres. History The Pythagoreans dealt with the regular solids, but the pyramid, prism, cone and cylinder were not studied until the Platonists. Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that the volume enclosed by a sphere is proportional to the cube of its radius.Paraphrased and taken in part from the ''1911 Encyclopædia Britannica''. Topics Basic topics in solid geometry and stereometry include: * incidence of planes and lines * dihedral angle and solid angle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
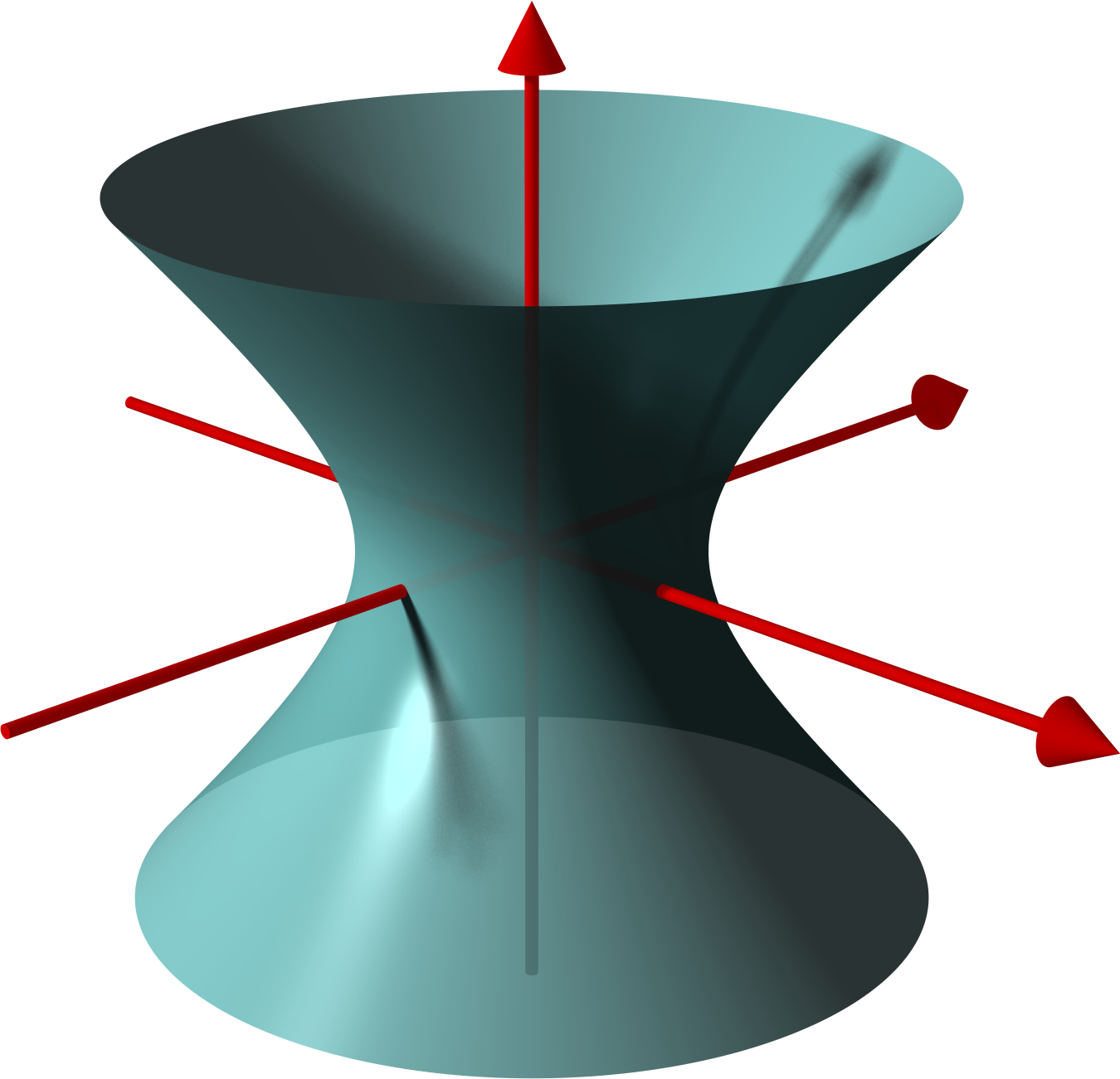
Hyperboloid Of Revolution
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation. A hyperboloid is a quadric surface, that is, a surface defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry. Given a hyperboloid, one can choose a Cartesian coordinate system such that the hyperboloid is defined by one of the following equations: : + - = 1, or : + - = -1. The coordinate axes are axes of symmetry of the hyperboloid and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonism
Platonism is the philosophy of Plato and philosophical systems closely derived from it, though contemporary platonists do not necessarily accept all of the doctrines of Plato. Platonism had a profound effect on Western thought. Platonism at least affirms the existence of abstract objects, which are asserted to exist in a third realm distinct from both the sensible external world and from the internal world of consciousness, and is the opposite of nominalism." Philosophers who affirm the existence of abstract objects are sometimes called platonists; those who deny their existence are sometimes called nominalists. The terms "platonism" and "nominalism" have established senses in the history of philosophy, where they denote positions that have little to do with the modern notion of an abstract object. In this connection, it is essential to bear in mind that modern platonists (with a small 'p') need not accept any of the doctrines of Plato, just as modern nominalists need not ac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid (geometry)
In geometry, a pyramid () is a polyhedron formed by connecting a polygonal base and a point, called the apex (geometry), apex. Each base edge and apex form a triangle, called a ''lateral face''. It is a cone, conic solid with polygonal base. A pyramid with an base has Vertex (geometry), vertices, Face (geometry), faces, and Edge (geometry), edges. All pyramids are Self-dual polyhedron, self-dual. A right pyramid has its apex directly above the centroid of its base. Nonright pyramids are called oblique pyramids. A regular pyramid has a regular polygon base and is usually implied to be a ''right pyramid''. When unspecified, a pyramid is usually assumed to be a ''regular'' square pyramid, like the physical pyramid structures. A triangle-based pyramid is more often called a tetrahedron. Among oblique pyramids, like acute and obtuse triangles, a pyramid can be called ''acute'' if its apex is above the interior of the base and ''obtuse'' if its apex is above the exterior of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term '' rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, the four concepts—''parallelepiped'' and ''cube'' in three dimensions, ''parallelogram'' and ''square'' in two dimensions—are defined, but in the context of a more general affine geometry, in which angles are not differentiated, only ''parallelograms'' and ''parallelepipeds'' exist. Three equivalent definitions of ''parallelepiped'' are *a polyhedron with six faces ( hexahedron), each of which is a parallelogram, *a hexahedron with three pairs of parallel faces, and *a prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all specific cases of parallelepiped. "Parallelepiped" is now usually pronounce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cuboid
In geometry, a cuboid is a hexahedron, a six-faced solid. Its faces are quadrilaterals. Cuboid means "like a cube", in the sense that by adjusting the length of the edges or the angles between edges and faces a cuboid can be transformed into a cube. In mathematical language a cuboid is a convex polyhedron, whose polyhedral graph is the same as that of a cube. Special cases are a cube, with 6 squares as faces, a rectangular prism, rectangular cuboid or rectangular box, with 6 rectangles as faces, for both, cube and rectangular prism, adjacent faces meet in a right angle. General cuboids By Euler's formula the numbers of faces ''F'', of vertices ''V'', and of edges ''E'' of any convex polyhedron are related by the formula ''F'' + ''V'' = ''E'' + 2. In the case of a cuboid this gives 6 + 8 = 12 + 2; that is, like a cube, a cuboid has 6 faces, 8 vertices, and 12 edges. Along with the rectangular cuboids, any parallel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
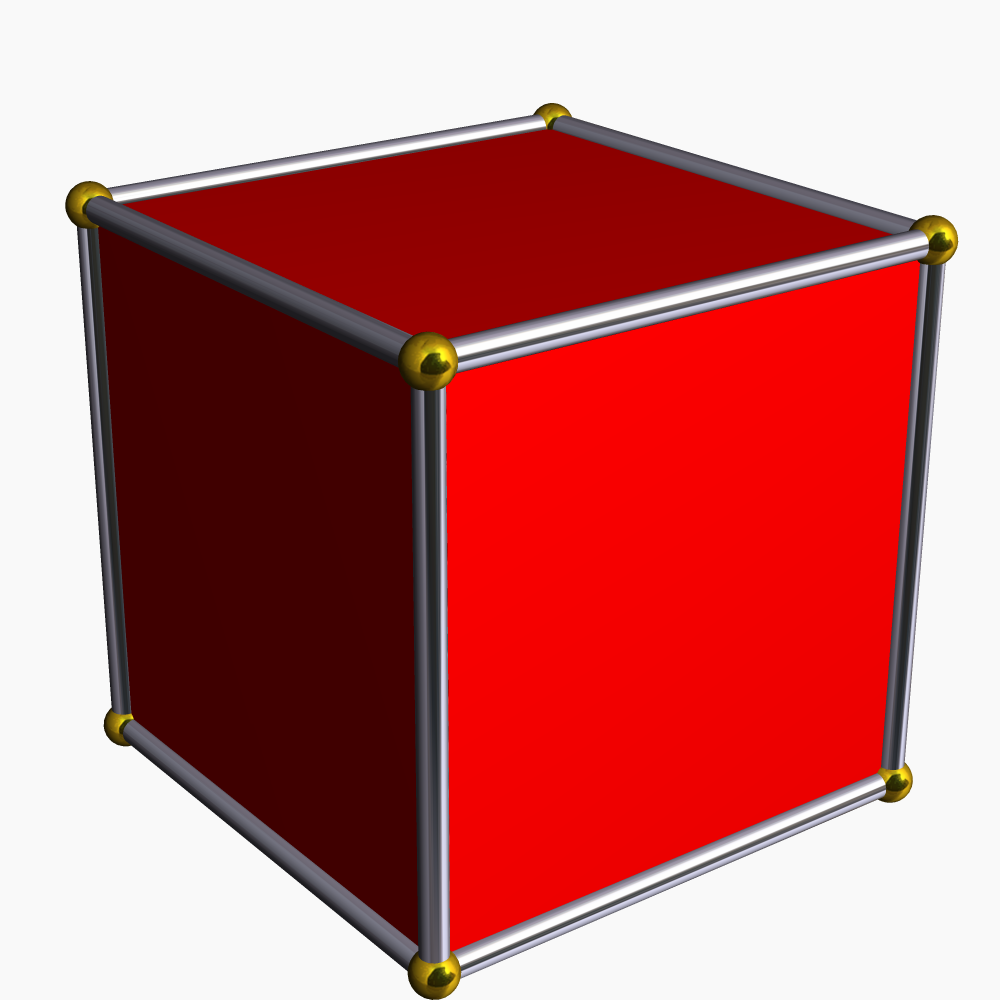
Cube (geometry)
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3- zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spherical tilin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the ''apex'' of the solid angle, and the object is said to ''subtend'' its solid angle at that point. In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a '' steradian'' (symbol: sr). One steradian corresponds to one unit of area on the unit sphere surrounding the apex, so an object that blocks all rays from the apex would cover a number of steradians equal to the total surface area of the unit sphere, 4\pi. Solid angles can also be measured in squares of angular measures such as degrees, minutes, and seconds. A small object nearby may subtend the same solid angle as a larger object farther away. For example, although the Moon is much small ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Angle
A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the union of a line and two half-planes that have this line as a common edge. In higher dimensions, a dihedral angle represents the angle between two hyperplanes. The planes of a flying machine are said to be at positive dihedral angle when both starboard and port main planes (commonly called wings) are upwardly inclined to the lateral axis. When downwardly inclined they are said to be at a negative dihedral angle. Mathematical background When the two intersecting planes are described in terms of Cartesian coordinates by the two equations : a_1 x + b_1 y + c_1 z + d_1 = 0 :a_2 x + b_2 y + c_2 z + d_2 = 0 the dihedral angle, \varphi between them is given by: :\cos \varphi = \frac and satisfies 0\le \varphi \le \pi/2. Alternatively, if an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line (mathematics)
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are One-dimensional space, one-dimensional objects, though they may exist in Two-dimensional Euclidean space, two, Three-dimensional space, three, or higher dimension spaces. The word ''line'' may also refer to a line segment in everyday life, which has two Point (geometry), points to denote its ends. Lines can be referred by two points that lay on it (e.g., \overleftrightarrow) or by a single letter (e.g., \ell). Euclid described a line as "breadthless length" which "lies evenly with respect to the points on itself"; he introduced several postulates as basic unprovable properties from which he constructed all of geometry, which is now called Euclidean geometry to avoid confusion with other geometries which have been introduced since the end of the 19th century (such as Non-Euclidean geometry, non-Euclidean, Projective geometry, projective and affine geometry). In modern mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane (mathematics)
In mathematics, a plane is a Euclidean ( flat), two-dimensional surface that extends indefinitely. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with one of a room's walls, infinitely extended, or they may enjoy an independent existence in their own right, as in the setting of two-dimensional Euclidean geometry. Sometimes the word ''plane'' is used more generally to describe a two-dimensional surface, for example the hyperbolic plane and elliptic plane. When working exclusively in two-dimensional Euclidean space, the definite article is used, so ''the'' plane refers to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional space, often in the plane. Euclidean geometry Euclid set forth the first great landmark of mathematical thought, an ax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incidence (geometry)
In geometry, an incidence relation is a heterogeneous relation that captures the idea being expressed when phrases such as "a point ''lies on'' a line" or "a line is ''contained in'' a plane" are used. The most basic incidence relation is that between a point, , and a line, , sometimes denoted . If the pair is called a ''flag''. There are many expressions used in common language to describe incidence (for example, a line ''passes through'' a point, a point ''lies in'' a plane, etc.) but the term "incidence" is preferred because it does not have the additional connotations that these other terms have, and it can be used in a symmetric manner. Statements such as "line intersects line " are also statements about incidence relations, but in this case, it is because this is a shorthand way of saying that "there exists a point that is incident with both line and line ". When one type of object can be thought of as a set of the other type of object (''viz''., a plane is a set of point ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.jpg)